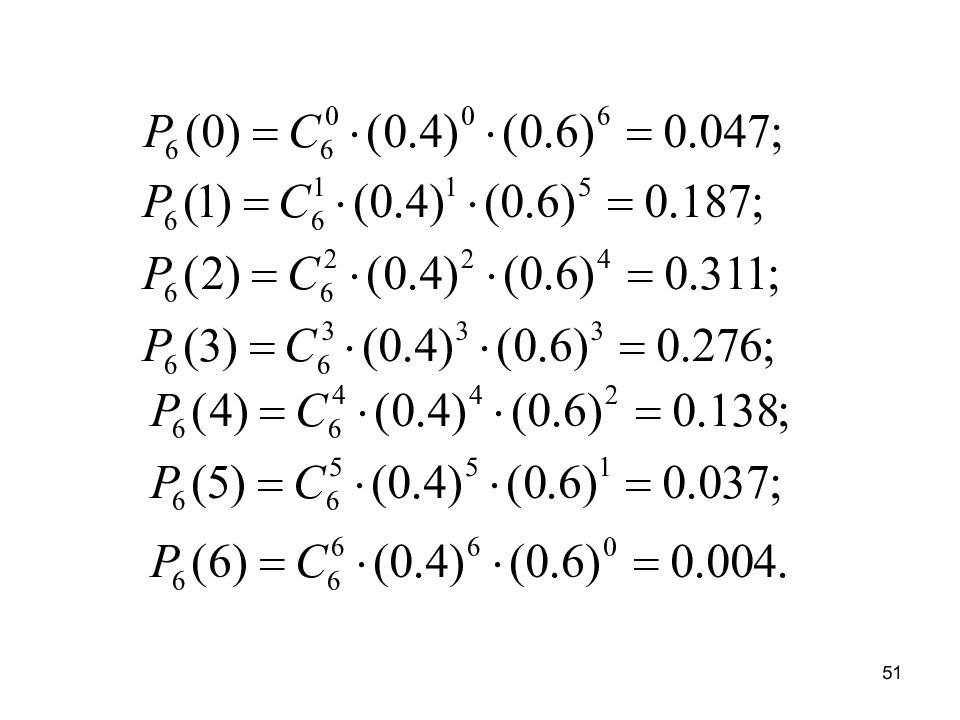Первый слайд презентации: Лекция «Основы теории вероятностей»
1 Лекция «Основы теории вероятностей» Часть 1. Вероятность случайных событий ГБОУ ВПО Кировская ГМА Минздрава РФ Кафедра физики и мединформатики Лектор О.Л. Короткова
Слайд 2: ЛИТЕРАТУРА:
2 ЛИТЕРАТУРА: Кудрявцев В.А., Короткова О.Л., Шилов О.И., Чупраков П.Г. «Теория вероятностей и математическая статистика» - Киров, 2007. «Основы высшей математики и математической статистики»/ И.В. Павлушков - М.: «ГЭОТАР-Медиа», 2006.
Слайд 3: ЛИТЕРАТУРА:
3 ЛИТЕРАТУРА: А.Н. Ремизов, А.Г. Максина «Сборник задач по медицинской и биологической физике» - М.: «Дрофа», 2001- 2007.
Слайд 4: ЛИТЕРАТУРА:
4 ЛИТЕРАТУРА: В.Е.Гмурман «Теория вероятностей и математическая статистика» - М.: «Высшая школа», 2003 -2007. В.Е.Гмурман «Руководство к решению задач по теории вероятностей и математической статистике» - М.: «Высшая школа», 2004 -2008.
Слайд 5: ПЛАН ЛЕКЦИИ:
5 ПЛАН ЛЕКЦИИ: Определение теории вероятностей. История возникновения теории вероятностей. Основные понятия теории вероятностей. Теоремы теории вероятностей. Элементы комбинаторики. Вероятность повторных событий.
Слайд 6: ОПРЕДЕЛЕНИЕ ТЕОРИИ ВЕРОЯТНОСТЕЙ:
6 Теория вероятностей - наука, изучающая закономерности массовых явлений, носящих случайный характер, позволяющая дать их количественную оценку. ОПРЕДЕЛЕНИЕ ТЕОРИИ ВЕРОЯТНОСТЕЙ:
7 ИСТОРИЯ ВОЗНИКНОВЕНИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ Корни теории вероятностей уходят далеко в глубь веков. Известно, что в древнейших государствах Китае, Индии, Египте, Греции уже использовались некоторые элементы вероятностных рассуждений для переписи населения, и даже определения численности войска неприятеля. Начало теории вероятностей как науки приписывают середине XVII века.
Слайд 8
8 1. Сколько раз надо бросать две игральные кости, чтобы случаев выпадения сразу двух шестерок было больше половины от общего числа бросаний? 2. Как справедливо разделить поставленные на кон двумя игроками деньги, если они по каким-то причинам прекратили игру преждевременно? Блез Паскаль (1623-1662) Шевалье де Мере (1607-1648)
Слайд 9
9 Х. Гюйгенс – «О расчётах в азартной игре». Якоб Бернулли – «Искусство предположений" первый основательный трактат по теории вероятностей: общая теория перестановок и сочетаний; закон больших чисел (связь между вероятностью какого-либо случайного события и частотой его появления, наблюдаемой непосредственно из опыта). Пьер Ферма (1601-1665) Якоб Бернулли (1654-1705) Христиан Гюйгенс (1623-1662) Б.Паскаль и П.Ферма – введение понятий математического ожидания, формулировка основных теорем сложения и произведения вероятностей.
Слайд 10
10 А.Муавр (1667-1754) П.Лапласс (1749-1827) К.Гаусс (1777-1855) С.Пуассон (1781-1840)
Слайд 11
11 Вторая половина XIX века: – русские учёные П.Л. Чебышев, А.А. Марков и А.М. Ляпунов. ХХ век: А.Н.Колмогоров. Теория вероятностей приобрела строгий математический вид и окончательно стала восприниматься как один из разделов математики.
Слайд 12: ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ
12 ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ Испытание (опыт, явление, процесс) – это наличие определенного комплекса условий, которые могут произойти без изменения любое количество раз. Исход – возможный результат испытания. Событие – это результат испытания, который интересует нас в условиях данной задачи. Вероятность события – это количественная мера возможности появления события в результате испытания.
Слайд 13: ПРИМЕР 1
13 ПРИМЕР 1. Испытание – бросание игральной кости (кубика с очками 1, 2, 3, 4, 5 и 6 на гранях). Исход – появление на верхней грани 1, 2, 3, 4, 5 или 6 очков. Событие – появление на верхней грани 1 очка. Событие, как правило, обозначают заглавной буквой начала латинского алфавита A, B, C…, например: А 1 - появление 1-го очка. Вероятность события. Вероятность события А обозначают Р(А ). Р(А 1 ) = 1/6 = 0,166666… ≈ 0,1667 = 16,67%.
Слайд 14: Виды случайных событий:
14 Виды случайных событий: I тип классификации по возможности появления в результате испытания: Случайным называется событие, которое в результате испытания (или в данных условиях) может либо произойти, либо не произойти. Достоверное событие. Невозможное событие. Противоположным для данного события называется событие, происходящее тогда и только тогда, когда не происходит события ( А ). Событие противоположное событию ( А ) принято обозначать ( Ā ), читается "не А".
Слайд 15: Классическое определение вероятности:
15 Классическое определение вероятности: Вероятность Р(А) появления события А равна отношению числа m А элементарных исходов благоприятствующих появлению события А к общему числу всех возможных элементарных исходов испытания n:
Слайд 16: ПРИМЕР 2:
16 ПРИМЕР 2: В урне находится 2 белых и 8 шаров черных – всего 10 шаров ( n= 10). Определить вероятность того, что наугад вынутый шар будет черным. Решение. Пусть событие А - вынуть белый шар. Число случаев благоприятствующих появлению события А: m А =2, число всевозможных исходов испытания n=10. Согласно формуле классической вероятности:
Слайд 17: Свойства вероятности:
17 Свойства вероятности: 1.Вероятность невозможного события m A = 0 : Вероятность достоверного события mА = n : Вероятность случайного события может принимать любые значения из отрезка [0÷1] : 0 Р(А) 1 или 0 р 1 ;
Слайд 18: Свойства вероятности:
18 Свойства вероятности: Вероятность события противоположного событию А равна разности между единицей и вероятностью события А: q = P( Ā )=1- P(A)=1- p ; Сумма вероятностей противоположных событий равна единице: p + q = 1.
Слайд 19: Виды случайных событий:
19 Виды случайных событий: I I тип классификации по отношению к появлению других событий в результате испытания: Два события называются совместными /несовместными, если появление одного из них не исключает / исключает появление другого. События А 1, А 2, А 3,..., А n называются единственно возможными в данном испытании, если появление хотя бы одного из них является событием достоверным. События А 1, А 2, А 3,..., А n или А i (где i=1,2,3,...,n) образуют полную группу событий, если они попарно несовместны и единственно возможны в этом испытании. Если А i (i=1,2,3,...,n) равновозможны, то они называются элементарными.
Слайд 20: ПРИМЕР 3:
20 ПРИМЕР 3: При бросании игрального одного кубика: событие А 6 - выпадение 6 очков, событие В - четное число очков. События А 4 и В, таким образом, совместны. При бросании монеты выпадение герба - событие А, выпадение решки - событие В. События А и В несовместны, так как одно исключает другое. Конец лекции 31.10.13 у КП
Слайд 21: Виды случайных событий:
21 Виды случайных событий: I I тип классификации по отношению к появлению других событий в результате испытания: Случайное событие В называется зависимым /независимым от случайного события А, если вероятность наступления события В зависит /не зависит от того, произошло или не произошло событие А. Вероятность зависимого события называется условной вероятностью и её принято обозначать Р(В / А) или Р А (В)
Слайд 22: ПРИМЕР 4:
22 ПРИМЕР 4: В урне находится 2 белых и 8 черных шаров – всего 10 шаров. Определить вероятность того, что второй наугад вынутый шар будет черным. Решение. Пусть событие Б 2 – вторым вынут белы й шар. Число случаев благоприятствующих появлению этого события m Б2 будет зависеть от следующих условий: Какой шар был вынут первым; Возвращается ли вынутый шар обратно в урну. Пусть вынутые шары возвращаются в урну. Тогда: общее количество шаров в урне остается неизменным ( n= 10 ) и независимо от цвета первого вынутого шара m Б2 =2. По классическому определению вероятности Р(Б 2 ) = m Б2 / n = 2/10=0,2.
Слайд 23
23 Пусть вынутые шары в урну не возвращаются Тогда: Если первым был вынут белый шар ( Б 1 ), то m Б2 =1, если же первым был вынут черный шар (Ч 1 ), то m Б2 =2. После вынимания первого шара в урне остается 9 шаров ( n=9). По определению условной вероятности: Р(Б 2 /Б 1 ) = m Б2 / n = 1/9; Р(Б 2 /Ч 1 ) = m Б2 / n = 2/9. Т.о., вероятность появления событие Б 2 зависит от предыдущего появления событий Б 1 или Ч 1, т.е. события Б 2 и Б 1, Б 2 и Ч 1 – попарно зависимые.
Слайд 24: Виды случайных событий:
24 Виды случайных событий: I I I тип классификации по результатам производимых действий : Суммой двух событий А и В называют событие С = А+В, заключающееся в наступлении или события А, или события В, или событий А и В одновременно (если события совместны). Произведением двух событий А и В называют событие D = А*В, заключающееся в одновременном наступлении (совмещении) событий А и В.
Слайд 25: ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
25 ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ Теорема 1(Т1). (Сложение вероятностей) : Вероятность наступления одного из двух несовместных событий А или В равна сумме вероятностей этих событий: Р(А+В)=Р(А)+Р(В) Сл.1.: Сумма вероятностей случайных событий А 1, А 2, А 3,..., А n, образующих полную группу - равна единице: Т2. (Умножение вероятностей) : Вероятность произведения (совместного наступления) двух независимых событий А и В равна произведению вероятностей этих событий: Р(АВ)=Р(А) · Р(В)= Р(В) · Р(А)
Слайд 26: ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
26 ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ Т3.: Вероятность произведения двух зависимых событий А и В равна произведению вероятности одного из них на условную вероятность другого: P(AB) = P(A) P(B/A) = Р(В) Р(А/В) Т4.: Пусть события А и В совместны. Вероятность суммы совместных событий равна сумме вероятностей этих событий без вероятности их совместного наступления:
Слайд 27: ПРИМЕР 5:
27 ПРИМЕР 5: Три лучника делают по одному выстрелу в одну и туже мишень. Вероятность попадания в мишень у первого лучника 80%, у второго – 90% и у третьего – 85%. Какова вероятность, что в мишень попадут две стрелы? Решение. Вероятности попадания каждым отдельным лучником по мишени: р 1 =80%=0,80, р 2 =90%=0,90, р 3 =85%=0,85. Вероятности промаха, соответственно: q 1 =1- р 1 =1-0,80=0,20, q 2 =1-0,90=0,10, q 3 =1-0,85=0,15. Событие А 2 – попадание в мишень двух стрел. Нам не важно, какие конкретно лучники попадут в цель, важно что двое из них попадут, а один – промажет.
Слайд 28
28 Т.е. событие А будет состоять из событий: первый и второй лучники попали и третий промазал, или первый и трепий попали и второй промазал, или второй и третий попали и первый промазал. Вероятность события А 2 найдем с использованием теорем произведения и суммы вероятностей (события независимые и несовместные): Р(А 2 ) = р 1 р 2 q 3 + р 1 q 2 р 3 + q 1 р 2 р 3 = = 0,80 · 0,90 · 0,15 + 0,80 · 0,10 · 0,85 + 0,20 · 0,90 · 0,85 = 0,329. Аналогичным образом можно вычислить вероятности попадания в мишень одной стрелы (А 1 ), трех стрел (А 3 ) или ни одной стрелы (А 0 ).
Слайд 29: ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
29 ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ Т5.: Вероятность осуществления хотя бы одного из случайных событий А 1, А 2, А 3,..., А n, независимых в совокупности, равна разности между единицей и произведением вероятностей событий им противоположных Ā 1, Ā 2,…, Ā n : P(A) = 1 - q 1 q 2 q 3... q n, где q 1 q 2 q 3... q n - вероятности, событий Ā 1, Ā 2,…, Ā n. Сл.2.: Если события А 1, А 2, А 3,..., А n имеют одинаковую вероятность, равную p, то вероятность появления хотя бы одного из этих событий: P(A) = 1 - q n.
Слайд 30: ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
30 ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ Т6. (Полная вероятность) : Вероятность случайного события ( А ), которое может произойти лишь при условии осуществления хотя бы одного из несовместных, образующих полную группу, случайных событий (гипотез) – или Н 1, или Н 2,..., или Н n, равна сумме произведений вероятностей каждой из этих гипотез на соответствующую условную вероятность появления события (A) : или с использованием знака суммы:
Слайд 31: ПРИМЕР 6:
31 ПРИМЕР 6: Для зачета по высшей математике было приготовлено 100 билетов содержащих три группы задач: в первой - 40 задач на дифференцирование, во второй - 40 задач на интегрирование и в третьей - 20 задач на составление дифференциальных уравнений. Какова вероятность того, что студент решит наугад взятую задачу, если он подготовился и умеет решать 30 задач на дифференцирование, 20 задач на интегрирование и 6 задач на составление дифференциальных уравнений?
Слайд 32
32 Решение. Эта задача может быть решена с использованием теоремы полной вероятности. Пусть событие А - студент решил наугад взятую задачу. Тогда можно предположить следующие варианты развития событий (гипотезы): или Н 1 - студент выбрал наугад билет, который содержал задачу из первой группы и произошло событие А - он её решил ; или Н 2 - студент выбрал наугад билет, который содержал задачу из второй группы и А; или Н 3 - студент выбрал наугад билет, который содержал задачу из третьей группы и А.
Слайд 33
33 Вероятность наступления события А при осуществлении одной из этих гипотез: По условию событие А может произойти в результате осуществления хотя бы одной из возможных несовместных гипотез: или Н 1, или Н 2, или Н 3, тогда вероятность осуществления события А, может быть найдена с использованием выражения:
Слайд 34: ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
34 ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ С3.: Формула Байеса позволяет решить две задачи: на основании предыдущего опыта (обобщенных статистических данных (гипотез)) позволяет оценивать вероятность интересующего нас события А ; на основании произведённого опыта (если при испытании произошло изучаемое событие А) оценивать вероятность той или иной гипотезы, не исключающей появление А. Томас Байес (1702-1761)
Слайд 35: ПРИМЕР 7:
35 ПРИМЕР 7: На основании условий предыдущего примера ( пример 6 ) имеем, что студент правильно выполнил выбранную наугад задачу. Возникает вопрос: к какой группе задач наиболее вероятно относилась решенная задача? Решение. По формуле Байеса вычислим вероятности принадлежности задач к каждой из групп: 1. 2. 3. Т.о., наиболее вероятно, что решенная задача будет из 1 группы, т.е. на нахождение производных
Слайд 36
36 ЭЛЕМЕНТЫ КОМБИНАТОРИКИ Термин «комбинаторика» был в ведён в математический обиход знаменитым Лейбницем. Готфрид Вильгельм Лейбниц (1646 — 1716) Область математики, в которой изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов, называется комбинаторикой.
Слайд 37
37 При составлении комбинаций из элементов конечного множества возможны следующие случаи: 1.Перестановки; 2.Размещения; 3.Сочетания. Факториал числа (n) равен последовательному произведению (n) чисел начиная с (1) и кончая (n): n! = 1 * 2 * 3 *.… * n Например, 3! = 1. 2. 3 = 6 5! = 1. 2. 3. 4. 5 = 120 При этом принято считать: 1! = 1, 0! = 1.
Слайд 38
38 Подмножества из (n) элементов множества, каждое из которых содержит все (n) элементов и которые отличаются друг от друга лишь порядком следования элементов, называют перестановками. Число перестановок из (n) элементов равно последовательному произведению (n) натуральных чисел, т. е.:
Слайд 39: ПРИМЕР 8
39 ПРИМЕР 8. Решение. По условию задачи количество слоников не меняется (=7), но меняется их последовательность. Число всевозможных перестановок будет равно: P n = n! = 1 · 2 · 3 · 4 · 5 · 6 · 7 = 5040 дней ≈ 13 лет и 9,5 месяцев. Сколько дней можно по-разному переставлять 7 слоников, если каждый день делать новую перестановку?
Слайд 40
40 Размещениями из (n) элементов некоторого множества по (m) элементов ( 1 m n ) называют подмножества, каждое из которых содержит ровно (m) различных элементов, выбранных из данного множества и которые отличаются друг от друга хотя бы одним элементом, либо порядком их следования. Число различных размещений, взятых из ( n ) элементов по ( m ), где (m n), равно произведению последовательных натуральных чисел, начиная с ( n ) и по (n - m + 1) включительно, т.е.:
Слайд 41: ПРИМЕР 9
41 ПРИМЕР 9. В классе 12 учебных предметов и 5 уроков в день. Сколько существует способов составить расписание на один день? Решение: Очевидно, что одно расписание от другого будет отличаться либо порядком следования предметов, либо хотя бы одним предметом. Следовательно, мы имеем дело с размещениями из ( n ) по ( m ):
Слайд 42
42 Сочетаниями из (n) элементов некоторого множества no (m) ( 1 m n), называют такие подмножества, каждое из которых содержит ровно (m) элементов множества и которые отличаются друг от друга хотя бы одним элементом (порядок элементов в сочетании не важен). Число всех возможных сочетаний из (n) элементов по (m) (m n) равно:
Слайд 43: ПРИМЕР 10
43 ПРИМЕР 10. Главврач должен сформировать бригаду врачей из 6 человек. Сколько существует способов сформировать одну бригаду из шести человек, если имеем 11 врачей различного профиля? Решение: Для решения этой задачи, очевидно, необходимо найти число сочетаний из (n = 11) по (m = 6) :
Слайд 44: Правила используемые при решении задач комбинаторики:
44 Правила используемые при решении задач комбинаторики: Правило суммы: Если некоторый объект (А) может быть выбран из совокупности объектов (m) способами, а объект (В) может быть выбран (n) способами, то или (А) или (В) можно выбрать ( n+m) способами. Правило произведения: Если некоторый объект (А) может быть выбран из совокупности объектов (m) способами и после каждого такого выбора объект (В) может быть выбран (n) способами, то пара (А) и (В) может быть выбрана в указанном порядке ( n m) способами.
Слайд 45: ПОВТОРЕНИЕ НЕЗАВИСИМЫХ ИСПЫТАНИЙ
45 ПОВТОРЕНИЕ НЕЗАВИСИМЫХ ИСПЫТАНИЙ Испытания называют независимыми относительно события А, если вероятность появления события А в каждом отдельном испытании не зависит от исходов предыдущих испытаний (например, появление герба при бросании монеты).
Слайд 46
46 В практике применения теории вероятностей особое значение имеют события, связанные с независимыми, повторными испытаниями для которых: 1) число испытаний (n) - конечно; 2) каждое испытание имеет только два исхода : либо А, либо Ā ; 3) испытания независимые; 4) вероятность Р(А) = р появления события А в каждом отдельном испытании постоянна p = const и Р(Ā) = 1 - р = q. Приведенные условия называются “схемой Бернулли”.
Слайд 47
47 Т.1. (теорема Бернулли): Если, при выполнении независимых повторных испытаний, для события А выполнялись все условия схемы Бернулли, то вероятность Р n (m) того, что в (n) испытаниях событие А произойдет ровно (m) раз выражается формулой Бернулли:
Слайд 48: Решение: Анализ ситуации показывает, что испытания подчиняются схеме Бернулли причём, q = 1-р =0,486. Тогда:
48 Решение: Анализ ситуации показывает, что испытания подчиняются схеме Бернулли причём, q = 1-р =0,486. Тогда: ПРИМЕР 11. Найти вероятность того, что в числе пяти появившихся на свет новорожденных три окажутся мужского пола, если, н а основании многолетних наблюдений, установлено, что вероятность рождения мальчика постоянна и равна (р = 0.514).
Слайд 49: Следствия из теоремы Бернулли:
49 Следствия из теоремы Бернулли: Наивероятнейшим числом (m 0 ) появлений события называется такое число повторений (по схеме Бернулли), вероятность которого является наибольшей. Сл.1.: В общем виде наивероятнейшее число (m0) осуществления случайного события (А) в (n) испытаниях, при условии выполнения схемы Бернулли, может быть определено на основании выражения:
Слайд 50
50 Расчёт орудия делает шесть выстрелов по мишени. Определить вероятности возможного числа попаданий, если вероятность попадания в цель при одном выстреле из орудия равна (0.4) и не меняется. Какое число попаданий при этом является наиболее вероятным? Решение: Воспользуемся формулой Бернулли, тогда вероятности числа попаданий в зависимости от (m) распределятся следующим образом: ПРИМЕР 12.
Слайд 53
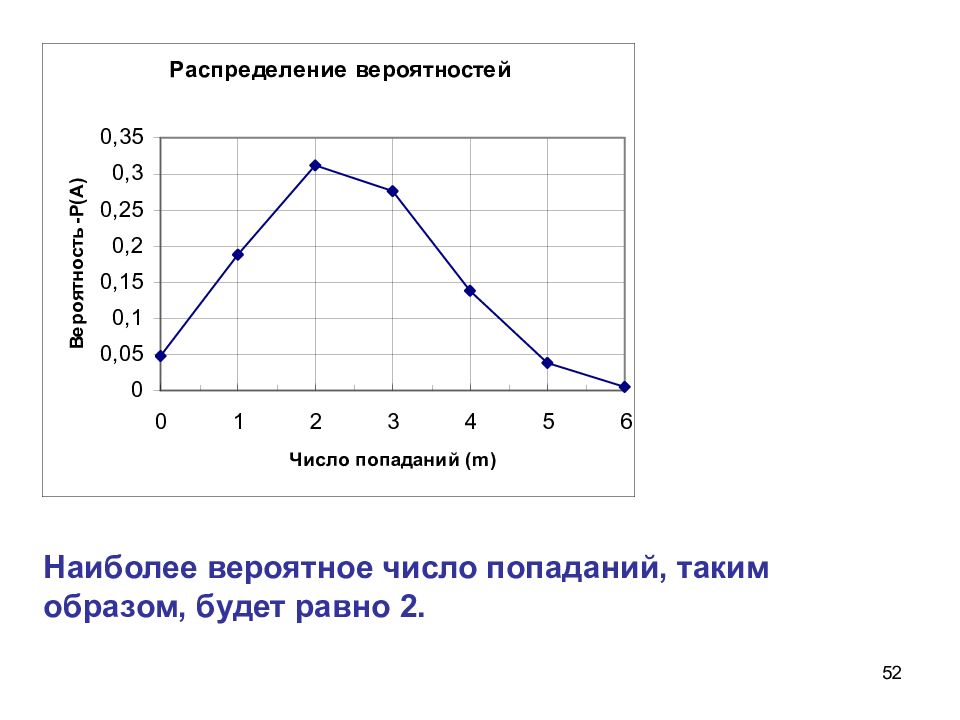
53 В общем виде наиболее вероятное число попаданий может быть вычислено следующим образом: Т.е., наиболее вероятное число попаданий будет равно 2.
Слайд 54: Приближенное вычисление вероятности повторных событий
54 Приближенное вычисление вероятности повторных событий Несложно заметить, что при достаточно большом числе n повторных испытаний пользоваться формулой Бернулли становится затруднительно, так как это связано с выполнением действий над большими числами. Пример 13: При условии выполнения схемы Бернулли найти вероятность того, что событие A произойдёт ровно 20 раз при 50 испытаниях, если p =0,1. Решение: Для решения такого рода задач мы пользуемся формулой Бернулли:
Слайд 55
55 Приближённая формула для нахождения вероятности когда число испытаний n велико, а p = q =0,5 была получена А. Муавром. Позднее С.Лапласом она была обобщена для произвольного p, отличного от нуля и единицы, то есть 0< p <1, и получила название – локальная теорема Лапласа (или теорема Муавра-Лапласа ).
Слайд 56
56 Т.2. (Локальная теорема Лапласса): Если вероятность р = Р(А) осуществления некоторого события А постоянна, то вероятность того, что в условиях схемы Бернулли в (n) испытаниях оно произойдет (m) раз, может быть найдена при помощи приближенной формулы:
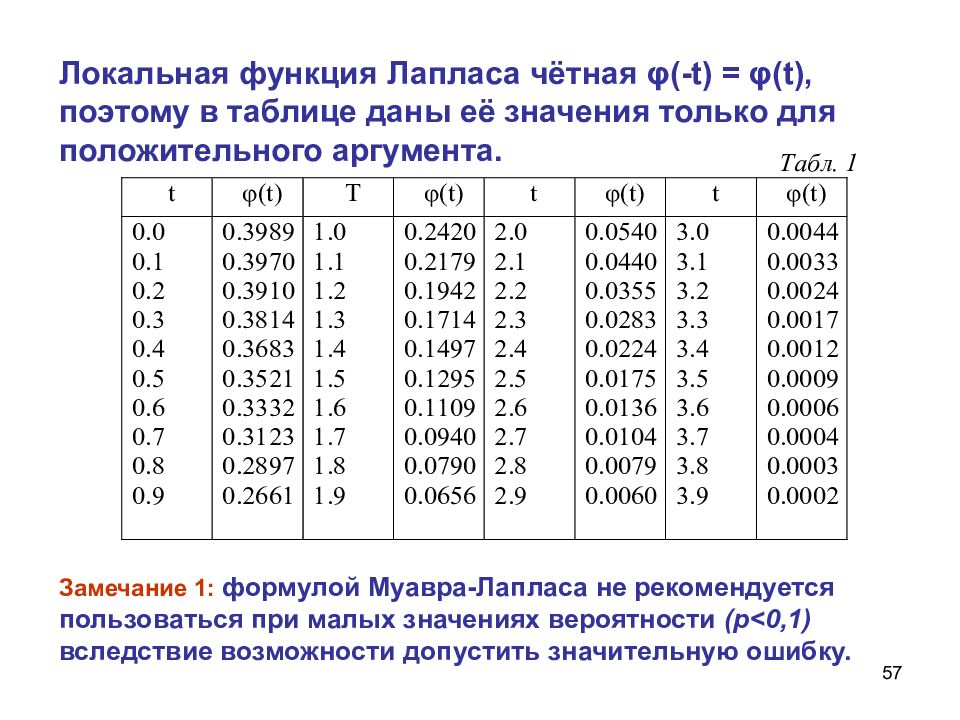
Слайд 57: Локальная функция Лапласа чётная φ (- t) = φ ( t), поэтому в таблице даны её значения только для положительного аргумента
57 Локальная функция Лапласа чётная φ (- t) = φ ( t), поэтому в таблице даны её значения только для положительного аргумента. Замечание 1 : формулой Муавра-Лапласа не рекомендуется пользоваться при малых значениях вероятности ( p<0,1 ) вследствие возможности допустить значительную ошибку.
Слайд 58: Интегральная теорема Лапласа
58 Интегральная теорема Лапласа Т.3. (Интегральная теорема Лапласа): При условии выполнения схемы Бернулли вероятность того, что в n испытаниях событие A появится не менее а 1, но и не более а 2 раз приближённо может быть определена следующим образом:
Слайд 59
59 Значения интегральной функции Лапласа найденные методами численного интегрирования для х >0, сведены в таблицу. Функция нечетная, т.е. Ф(-х) = - Ф(х).
Слайд 60: Формула Пуассона
60 Формула Пуассона При больших значениях n (не менее нескольких десятков или сотен) лучше ориентироваться на значение Параметра μ = nр. Если оно находится в пределах 0< μ <10, следует воспользоваться приближённой формулой Пуассона : Следует отметить, что формула Пуассона находит широкое применение в теории массового обслуживания, а, следовательно, и в медицине.
Слайд 61: ПРИМЕР 14
61 ПРИМЕР 14. Вероятность повторного заболевания гриппом в течение года равна р =0,15. Какова вероятность того, что из 100 человек 20 заболеют гриппом повторно? Решение: для решения этой задачи воспользуемся локальной теоремой Лапласа:
Слайд 62: ПРИМЕР 15
62 ПРИМЕР 15. Вероятность того, что упаковка лекарственного препарата не прошла проверку ОТК, равна p =0,2. Найти вероятность того, что при формировании партии для поставки в аптеку среди 400 случайным образом отобранных упаковок непроверенных окажется от 70 до 100. Решение: Согласно условию p =0,2; q =0,8; n =400; а 1 =70; а 2 =100. Находим пределы интегрирования х 1 и х 2 :
Последний слайд презентации: Лекция «Основы теории вероятностей»: ПРИМЕР 16
63 ПРИМЕР 16. При массовом производстве новокаина вероятность появления бракованной ампулы относительно постоянна и составляет в среднем 0,001. Следует выяснить, какова вероятность того, что в партии из 1000 ампул 2 будут бракованными? Решение: По условию: n =1000, m =2, p =0,001, причём параметр μ = np =1 находится в пределах 0<μ<10, когда рекомендуется воспользоваться формулой Пуассона: