Первый слайд презентации: Лекция 2
Санитарная статистика, её значение для здравоохранения. Основные методы статистической обработки медицинской информации.
Слайд 2
Статистика – наука, изучающая закономерности массовых общественных явлений методом обобщающих показателей. Санитарная статистика – изучает вопросы, связанные с медициной, гигиеной, организацией здравоохранения и имеет свои специфические разделы: статистику здоровья населения, статистику здравоохранения и научную статистику
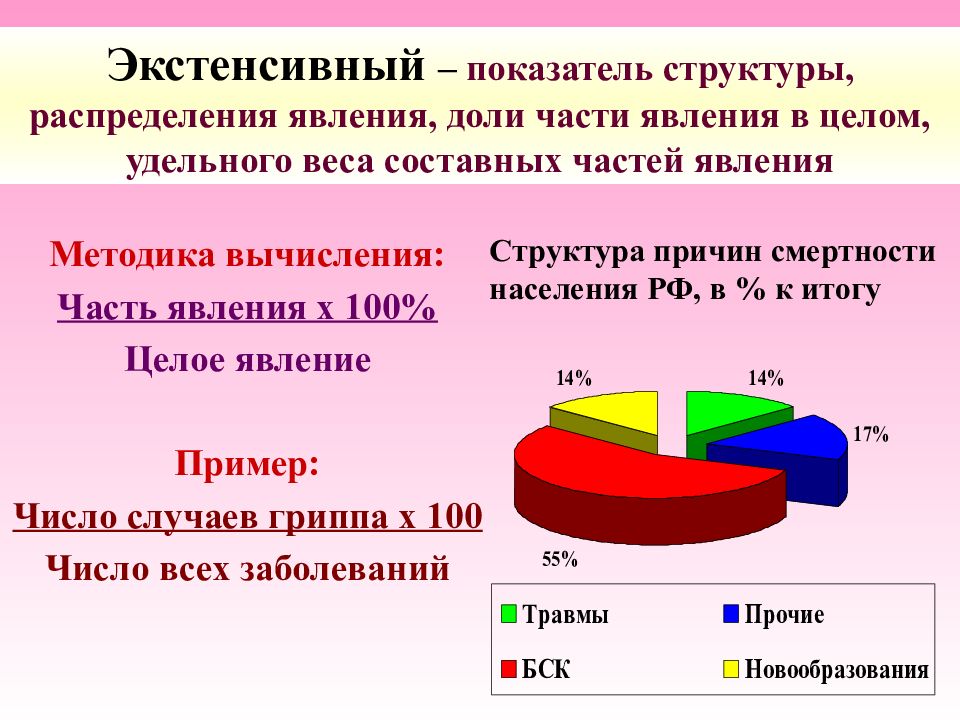
Методика вычисления: Часть явления х 100% Целое явление Пример: Число случаев гриппа х 100 Число всех заболеваний Структура причин смертности населения РФ, в % к итогу
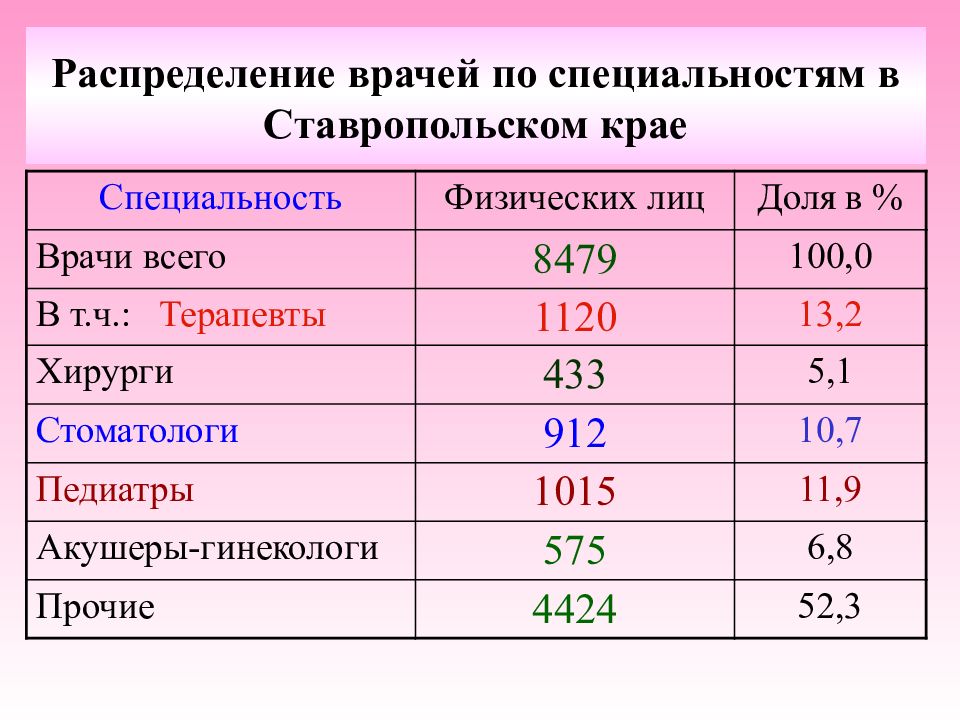
Слайд 4: Распределение врачей по специальностям в Ставропольском крае
Специальность Физических лиц Доля в % Врачи всего 8479 100,0 В т.ч.: Терапевты 1120 13,2 Хирурги 433 5,1 Стоматологи 912 10,7 Педиатры 1015 11,9 Акушеры-гинекологи 575 6,8 Прочие 4424 52,3
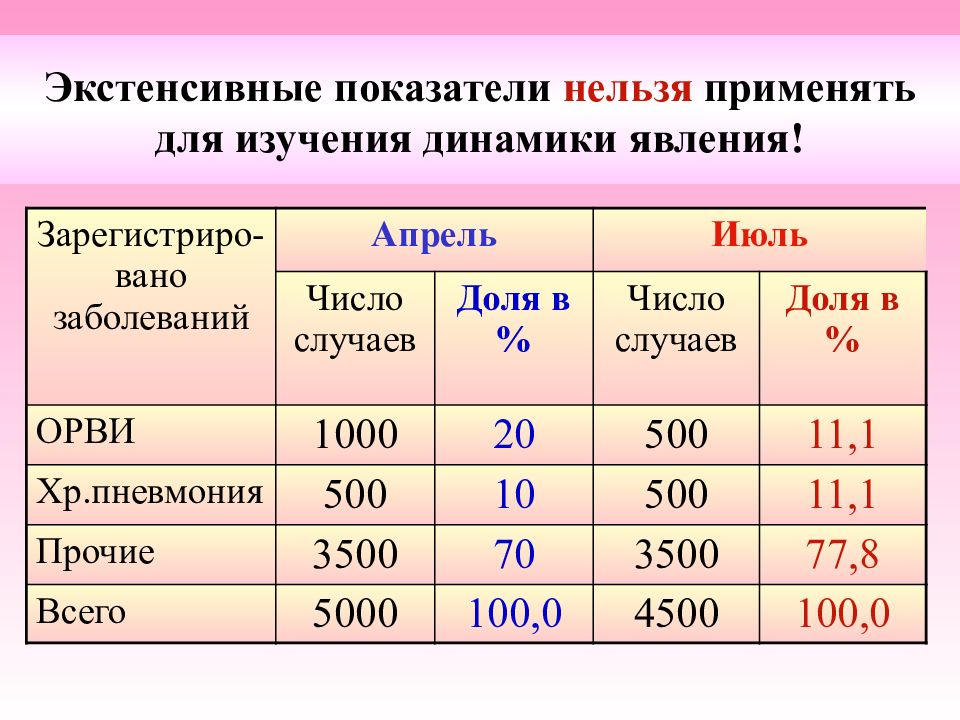
Зарегистриро-вано заболеваний Апрель Июль Число случаев Доля в % Число случаев Доля в % ОРВИ 1000 20 500 11,1 Хр.пневмония 500 10 500 11,1 Прочие 3500 70 3500 77,8 Всего 5000 100,0 4500 100,0
Слайд 6: Интенсивный показатель – показатель частоты, распространенности явления в однородной среде
Методика расчета: Явление х Основание показателя (100, 1000) Среда, продуцирующая это явление Общий уровень смертности: Число умерших за год х 1000 Среднегодовая численность населения
Слайд 7: Общие и специальные интенсивные показатели
Общий уровень рождаемости: Число родившихся за год детей х 1000 Среднегодовая численность населения Специальный интенсивный показатель Уровень общей плодовитости: Число родившихся за год детей х 1000 Численность женщин от 15 до 49 лет
Слайд 8: Показатель соотношения – характеризует частоту, распространенность явлений в разнородных средах
Методика расчета : Явление × основание показателя (100, 1000) Среду, не продуцирующую явление Обеспеченность населения больничными койками Число среднегодовых коек × 1000 Среднегодовую численность населения
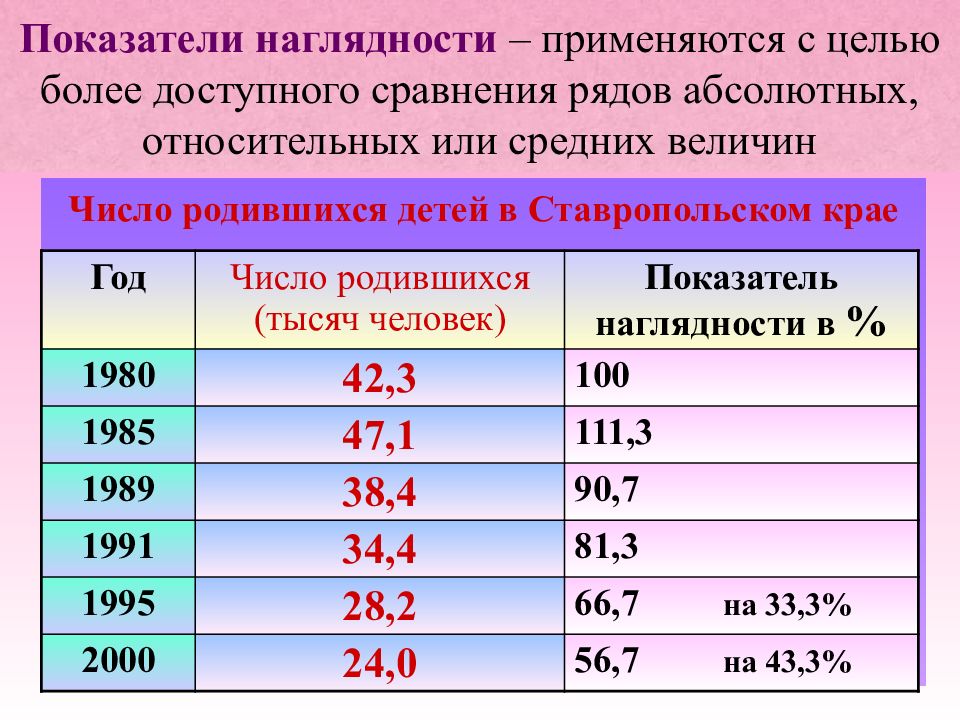
Слайд 9: Показатели наглядности – применяются с целью более доступного сравнения рядов абсолютных, относительных или средних величин
Число родившихся детей в Ставропольском крае Год Число родившихся (тысяч человек) Показатель наглядности в % 1980 42,3 100 1985 47,1 111,3 1989 38,4 90,7 1991 34,4 81,3 1995 28,2 66,7 на 33,3% 2000 24,0 56,7 на 43,3%
Применяются средние величины: При изучении физического развития (стандарты физического развития) В ЛПУ при расчете показателей работы: средняя нагрузка врача, средняя длительность лечения и т.д. При интерпретации данных объективного обследования пациентов В органах санэпиднадзора: средние нормы жилой площади на 1 человека, средние нормы белков, жиров, углеводов в дневном рационе взрослых и детей
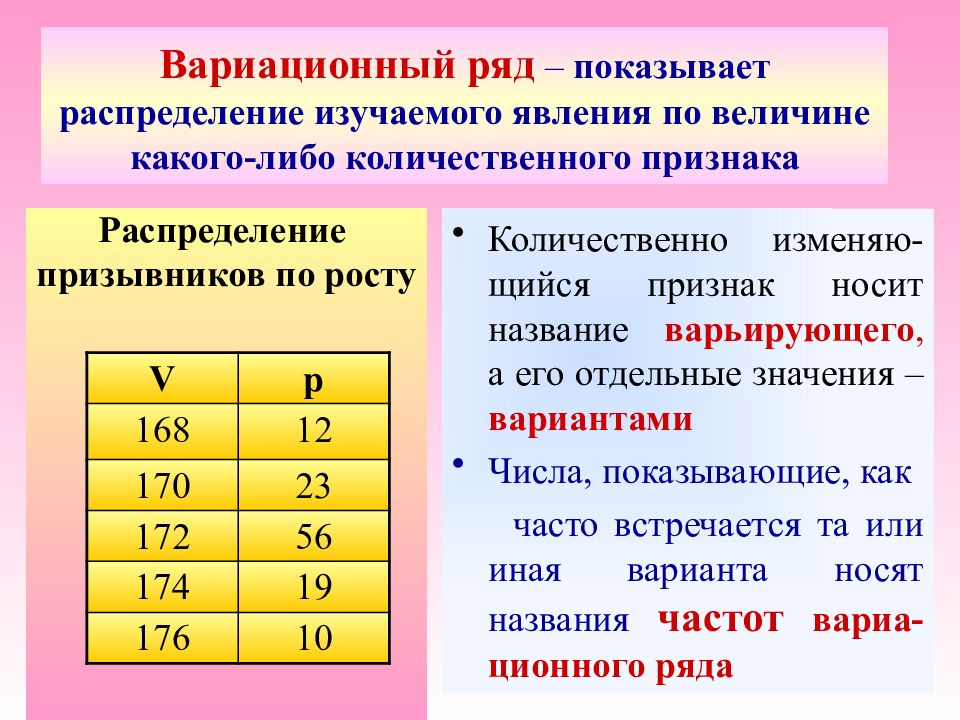
Распределение призывников по росту Количественно изменяю-щийся признак носит название варьирующего, а его отдельные значения – вариантами Числа, показывающие, как часто встречается та или иная варианта носят названия частот вариа-ционного ряда V p 168 12 170 23 172 56 174 19 176 10
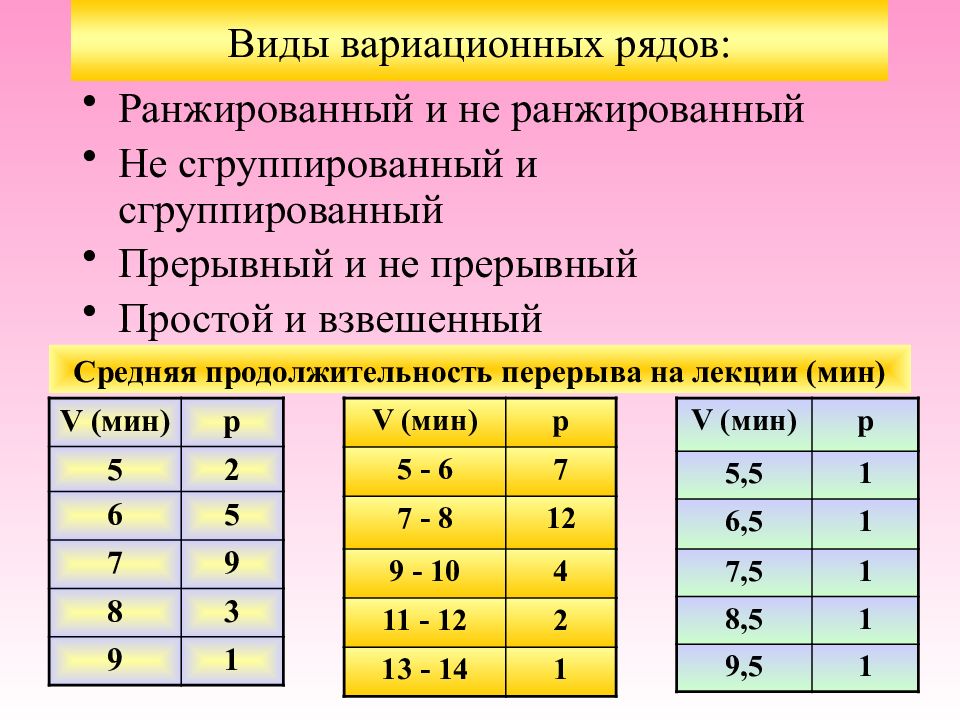
Слайд 12: Виды вариационных рядов:
Ранжированный и не ранжированный Не сгруппированный и сгруппированный Прерывный и не прерывный Простой и взвешенный V (мин) p 5 2 6 5 7 9 8 3 9 1 Средняя продолжительность перерыва на лекции (мин) V (мин) p 5 - 6 7 7 - 8 12 9 - 10 4 11 - 12 2 13 - 14 1 V (мин) p 5,5 1 6,5 1 7,5 1 8,5 1 9,5 1
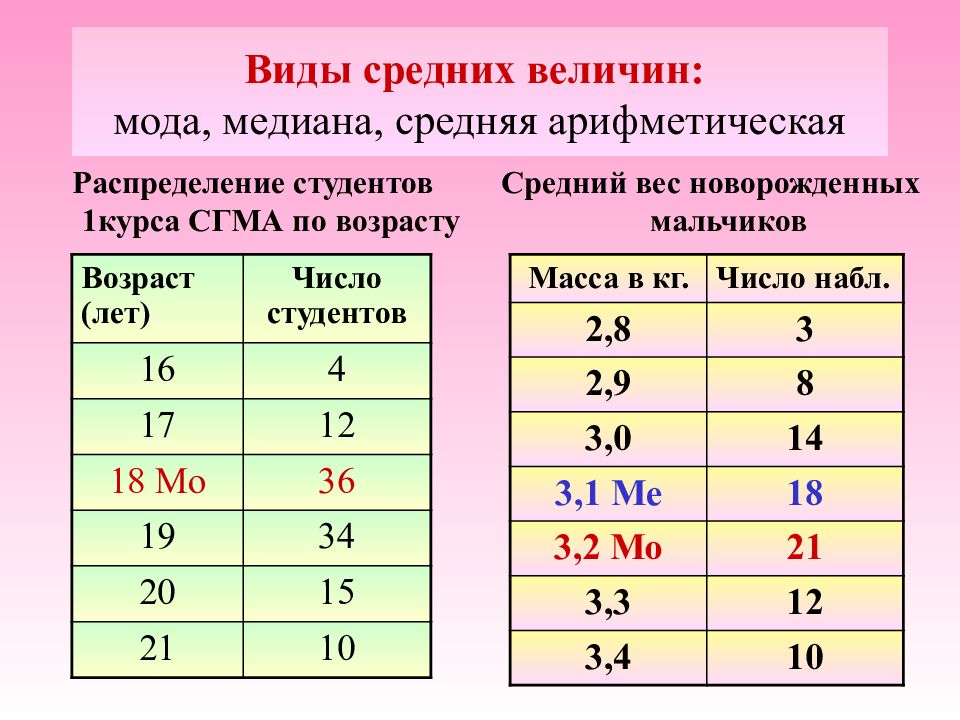
Слайд 13: Виды средних величин: мода, медиана, средняя арифметическая
Распределение студентов 1курса СГМА по возрасту Средний вес новорожденных мальчиков Возраст (лет) Число студентов 16 4 17 12 18 Мо 36 19 34 20 15 21 10 Масса в кг. Число набл. 2,8 3 2,9 8 3,0 14 3,1 Ме 18 3,2 Мо 21 3,3 12 3,4 10
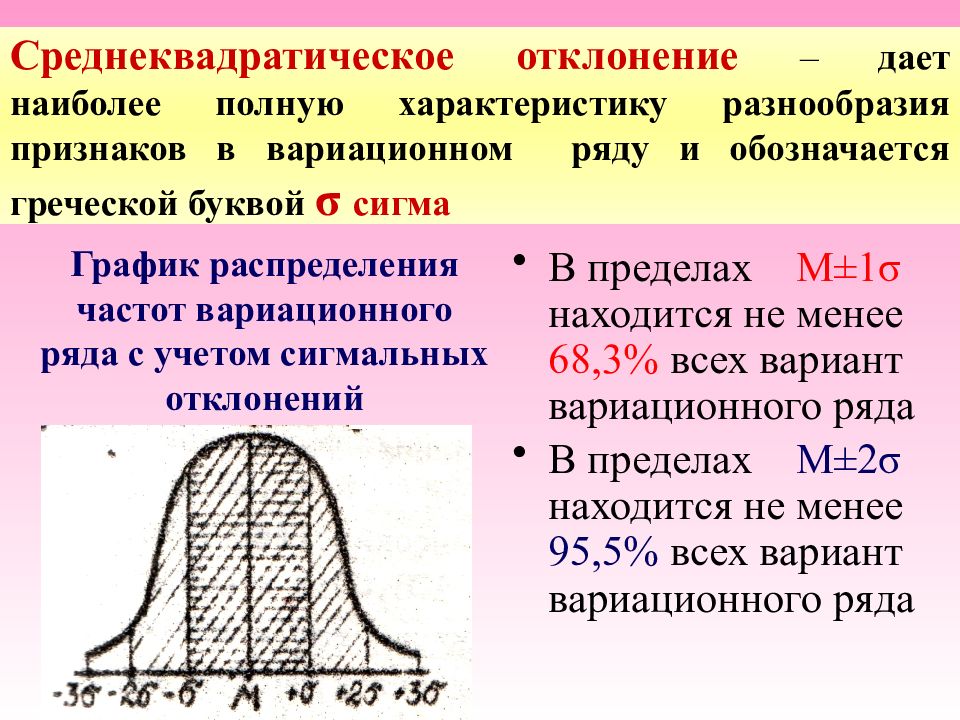
Слайд 14: Среднеквадратическое отклонение – дает наиболее полную характеристику разнообразия признаков в вариационном ряду и обозначается греческой буквой σ сигма
В пределах М ± 1 σ находится не менее 68,3% всех вариант вариационного ряда В пределах М ± 2 σ находится не менее 95,5% всех вариант вариационного ряда График распределения частот вариационного ряда с учетом сигмальных отклонений
Слайд 15: Три способа оценки достоверности средних и относительных показателей
Ошибка репрезентативности показателя: Доверительные границы : Мген = Мвыб ±tm P ген = Рвыб ±tm Значения t : t =1, при р=68,3%, t =2, при р=95,5%, t =3, при р=99,7%, t =4, при р=99,9%, Достоверность разности средних и относительных величин по критерию Стьюдента ( t)
Слайд 16: Достоверность разности относительных показателей
Летальность в двух больницах В больнице А: В больнице Б: Показатели летальности в двух больницах достоверно отличаются
Слайд 17: Статистическое изучение связи между явлениями
Функциональная связь – каждому определенному значению влияющего признака (х) всегда соответствует строго определенное, единственное значение результирующего признака (у). Функциональную связь можно представить в виде уравнения, формулы (радиус –площадь круга – объем шара) Корреляционная связь – каждому конкретному значению влияющего признака соответствует не одно значение, а целое распределение случайных значений (вариация) результирующего признака. Для одного и того же возраста или роста мы можем получить вариацию веса, мышечной силы и т.д.
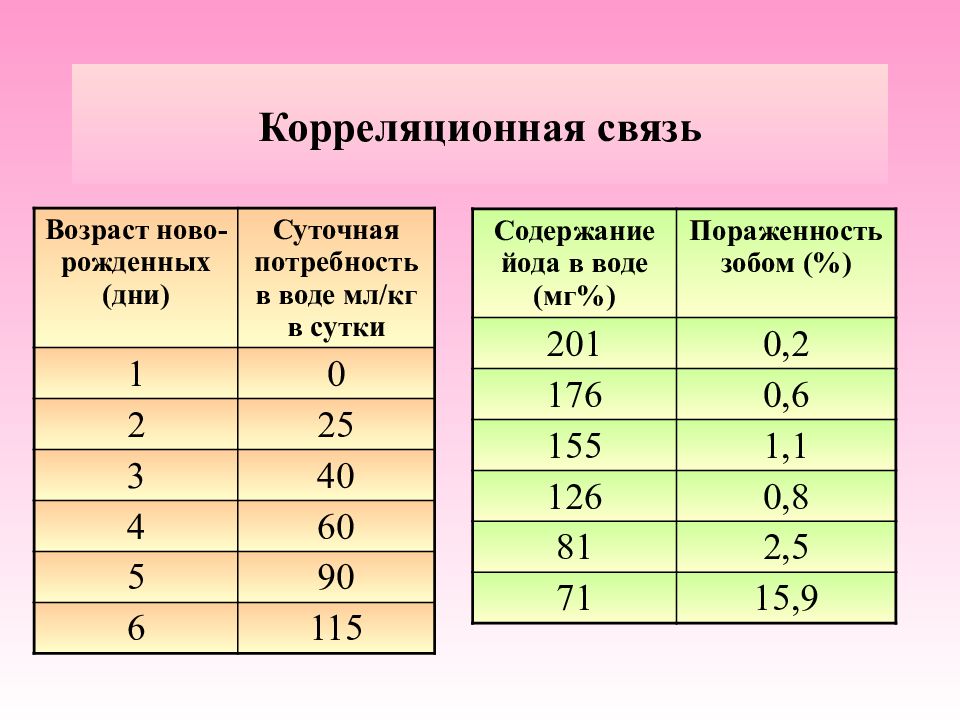
Слайд 18: Корреляционная связь
Возраст ново-рожденных (дни) Суточная потребность в воде мл/кг в сутки 1 0 2 25 3 40 4 60 5 90 6 115 Содержание йода в воде (мг%) Пораженность зобом (%) 201 0,2 176 0,6 155 1,1 126 0,8 81 2,5 71 15,9
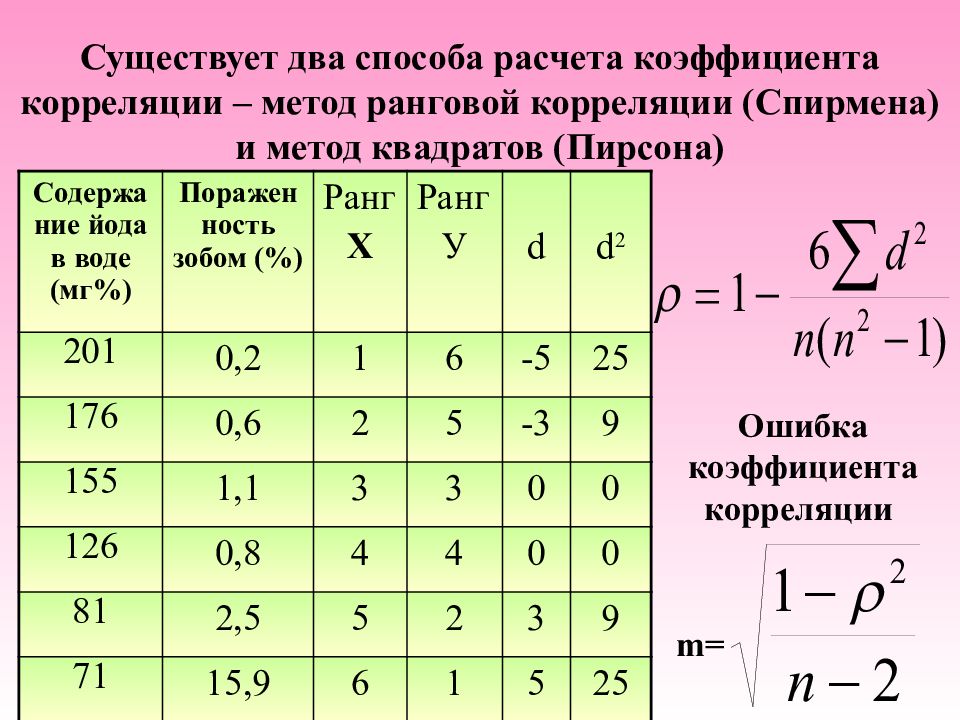
Слайд 19: Существует два способа расчета коэффициента корреляции – метод ранговой корреляции (Спирмена) и метод квадратов (Пирсона)
Содержание йода в воде (мг%) Пораженность зобом (%) Ранг Х Ранг У d d 2 201 0,2 1 6 -5 25 176 0,6 2 5 -3 9 155 1,1 3 3 0 0 126 0,8 4 4 0 0 81 2,5 5 2 3 9 71 15,9 6 1 5 25 Ошибка коэффициента корреляции m=
Слайд 20: Определение силы и направления связи по коэффициенту корреляции
Оценка корреляции Величина коэффициента Прямой корреляции + Обратной корреляции ─ Связь отсутствует 0 0 Слабая связь От 0 до +0,3 От -0,3 до 0 Средняя связь От +0,3 до +0,7 От -0,7 до -0,3 Сильная связь От +07 до +1,0 От -1,0 до -0,7 Полная связь +1,0 -1,0
Последний слайд презентации: Лекция 2: Стандартизация – метод расчета условных (стандартизованных) показателей, заменяющих интенсивные величины в случаях, когда сравнение последних затруднено из-за несопоставимости состава групп
Применяется для сравнения общих интенсивных показателей, вычисленных в неоднородной по структуре среде (разный состав населения по возрас-ту, полу, образу жизни, уровню образования и т.д.) Сущность стандартизации заключается в вычислении обобщенных (стандартизованных) показателей Стандартизованные показатели характеризуют только соотношение, но не истинные размеры явления. Могут быть использованы только для целей сравнения