Лекция 2 Метод контурных токов ( МКТ). Метод узловых потенциалов (МУП). Потенциальная диаграмма. Баланс мощностей (БМ). ОмГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция №2. Тэттэр А.Ю., Пономарев А.В.
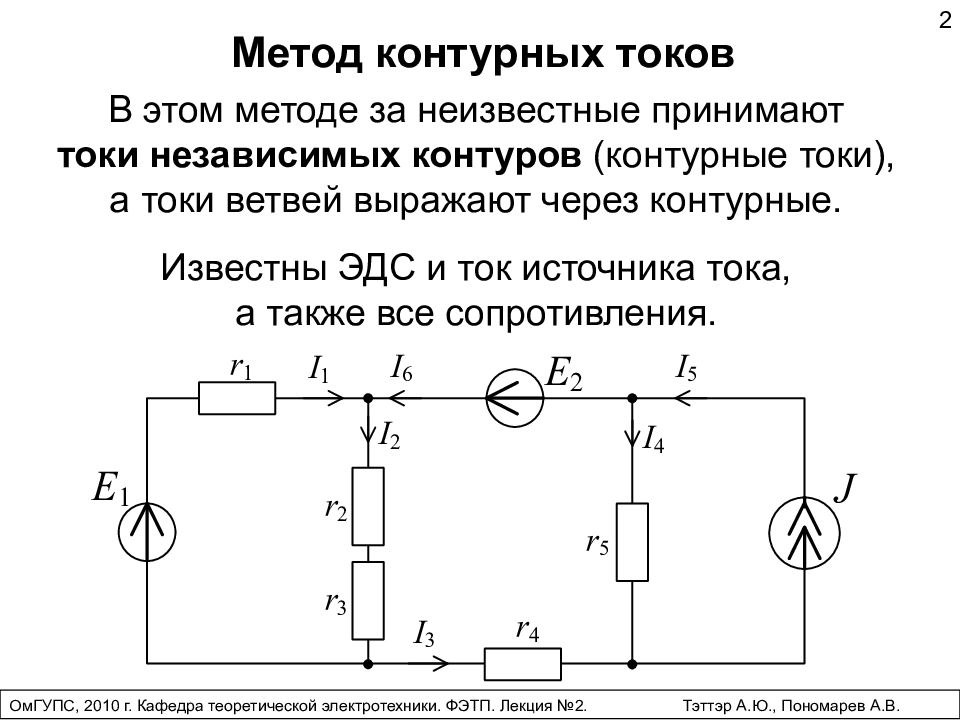
2 Известны ЭДС и ток источника тока, а также все сопротивления. Метод контурных токов В этом методе за неизвестные принимают токи независимых контуров (контурные токи), а токи ветвей выражают через контурные. ОмГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция №2. Тэттэр А.Ю., Пономарев А.В.
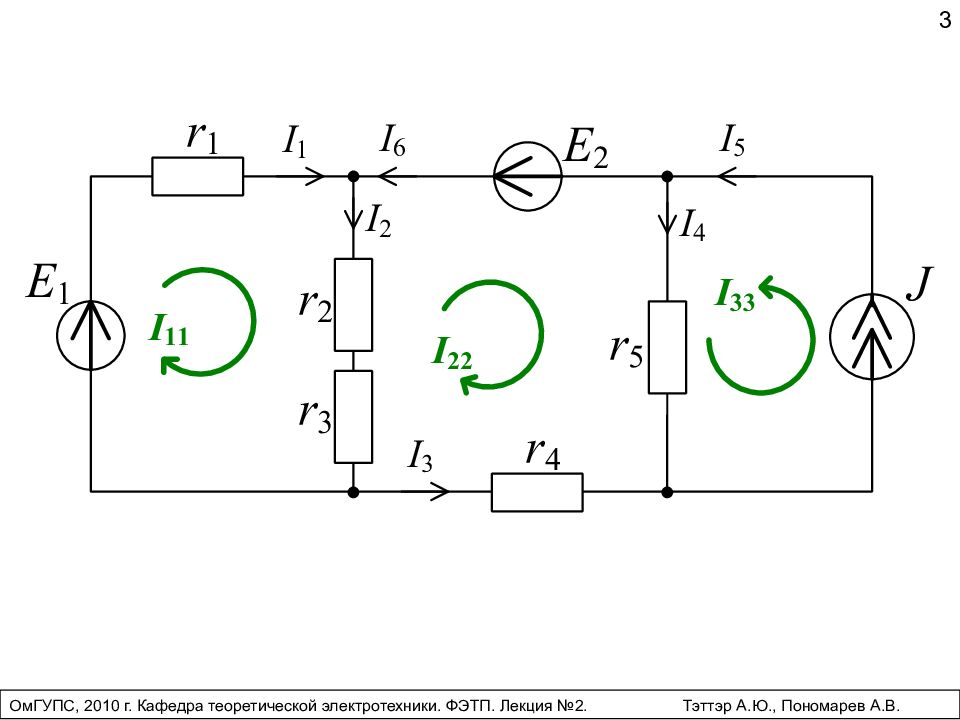
3 ОмГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция №2. Тэттэр А.Ю., Пономарев А.В.
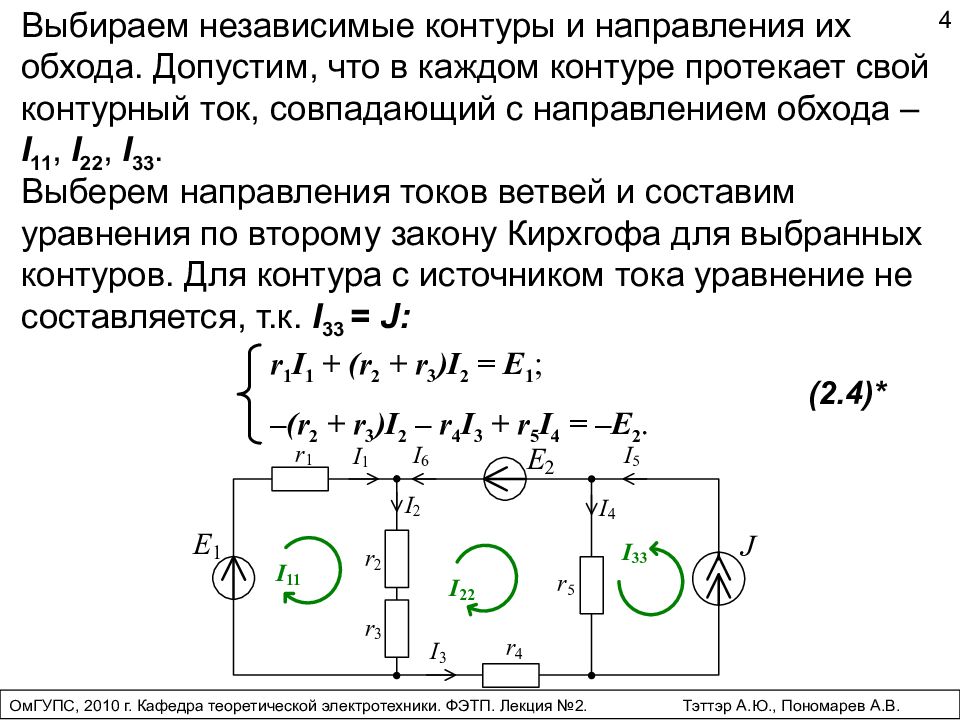
Выберем направления токов ветвей и составим уравнения по второму закону Кирхгофа для выбранных контуров. Для контура с источником тока уравнение не составляется, т.к. I 33 = J: r 1 I 1 + (r 2 + r 3 )I 2 = E 1 ; –(r 2 + r 3 )I 2 – r 4 I 3 + r 5 I 4 = –E 2. (2.4)* 4 ОмГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция №2. Тэттэр А.Ю., Пономарев А.В. Выбираем независимые контуры и направления их обхода. Допустим, что в каждом контуре протекает свой контурный ток, совпадающий с направлением обхода – I 11, I 22, I 33.
* Здесь и далее номера формул соответствуют учебному пособию [1]: В.Н. Зажирко, А.Ю. Тэттэр Основы теории цепей постоянного и переменного тока, Омск, 2006 5 ОмГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция №2. Тэттэр А.Ю., Пономарев А.В.
Подставим их в систему (2.4) : Выразим токи ветвей через контурные: r 1 I 11 + ( r 2 + r 3 ) ( I 11 – I 2 2 ) = E 1 ; – ( r 2 + r 3 )( I 11 – I 22 ) – r 4 (– I 22 ) + r 5 ( I 22 + I 33 ) = –E 2 6 ОмГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция №2. Тэттэр А.Ю., Пономарев А.В. I 1 = I 11 ; I 2 = I 11 – I 22 ; I 6 = I 3 = – I 22 ; I 4 = I 22 + I 33 ; I 5 = I 33 ; I 33 = J ; I 5 = J.
После группировки получим: ( r 1 + r 2 + r 3 )I 11 – ( r 2 + r 3 ) I 22 = E 1 ; – ( r 2 + r 3 ) I 11 + ( r 2 + r 3 + r 4 + r 5 ) I 22 + r 5 I 33 = – E 2. r 11 r 12 E 11 E 22 r 21 r 22 r 23 В общем виде: r 1 1 I 11 + r 12 I 22 + r 13 I 33 = E 11 ; r 21 I 11 + r 22 I 22 + r 23 I 33 = E 22. 7 ОмГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция №2. Тэттэр А.Ю., Пономарев А.В.
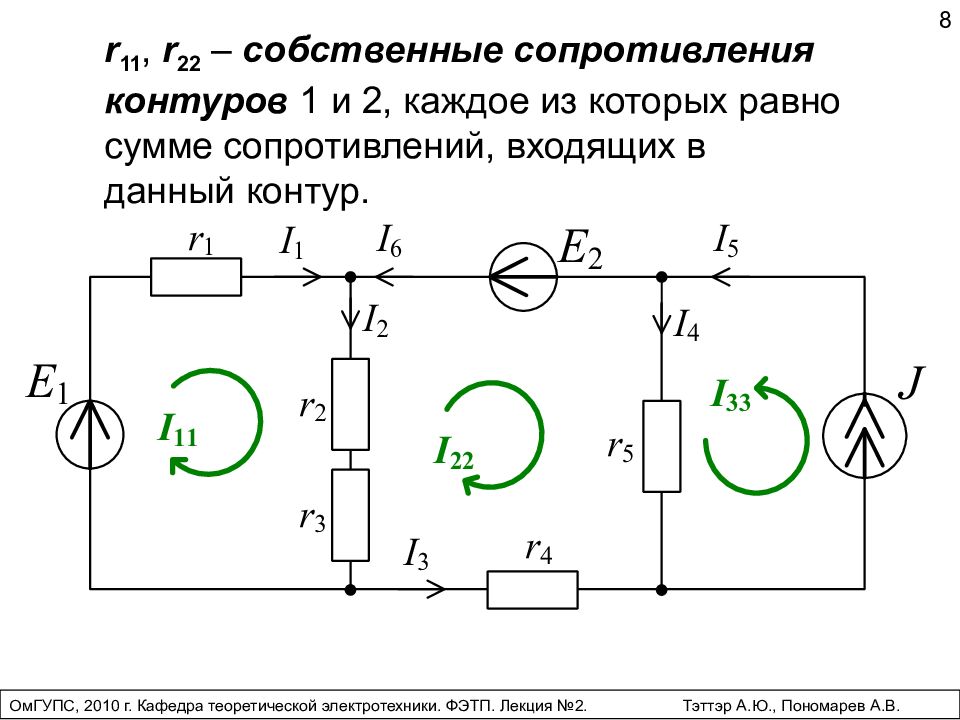
r 11, r 22 – собственные сопротивления контуров 1 и 2, каждое из которых равно сумме сопротивлений, входящих в данный контур. 8 ОмГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция №2. Тэттэр А.Ю., Пономарев А.В.
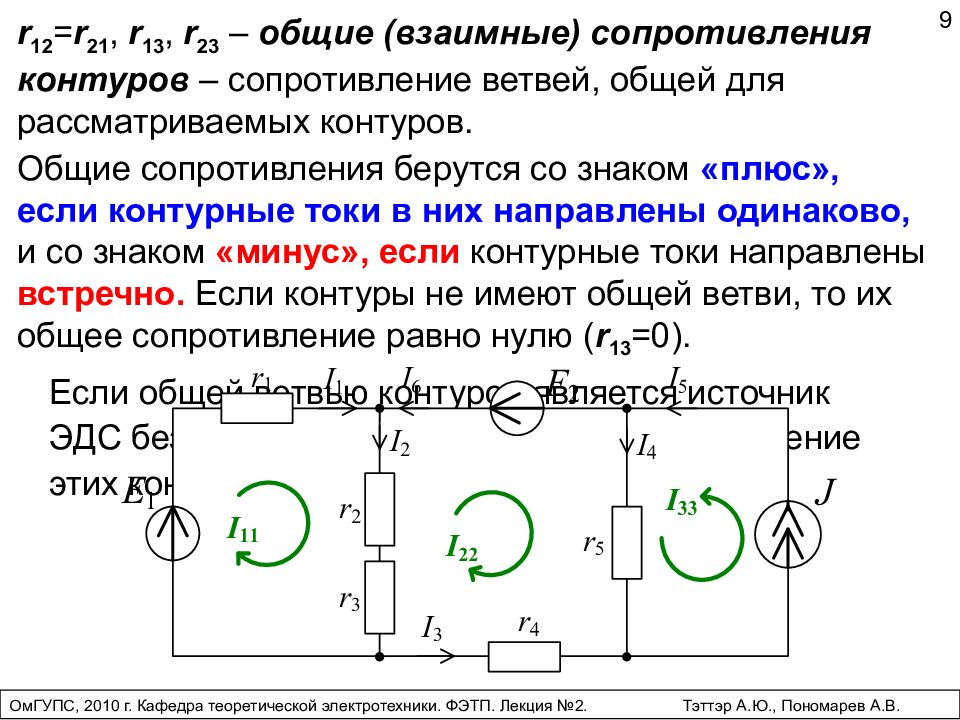
Общие сопротивления берутся со знаком «плюс», если контурные токи в них направлены одинаково, и со знаком «минус», если контурные токи направлены встречно. Если контуры не имеют общей ветви, то их общее сопротивление равно нулю ( r 13 =0). 9 ОмГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция №2. Тэттэр А.Ю., Пономарев А.В. r 1 2 = r 21, r 13, r 23 – общие (взаимные) сопротивления контуров – сопротивление ветвей, общей для рассматриваемых контуров. Если общей ветвью контуров является источник ЭДС без сопротивления, то общее сопротивление этих контуров равно нулю.
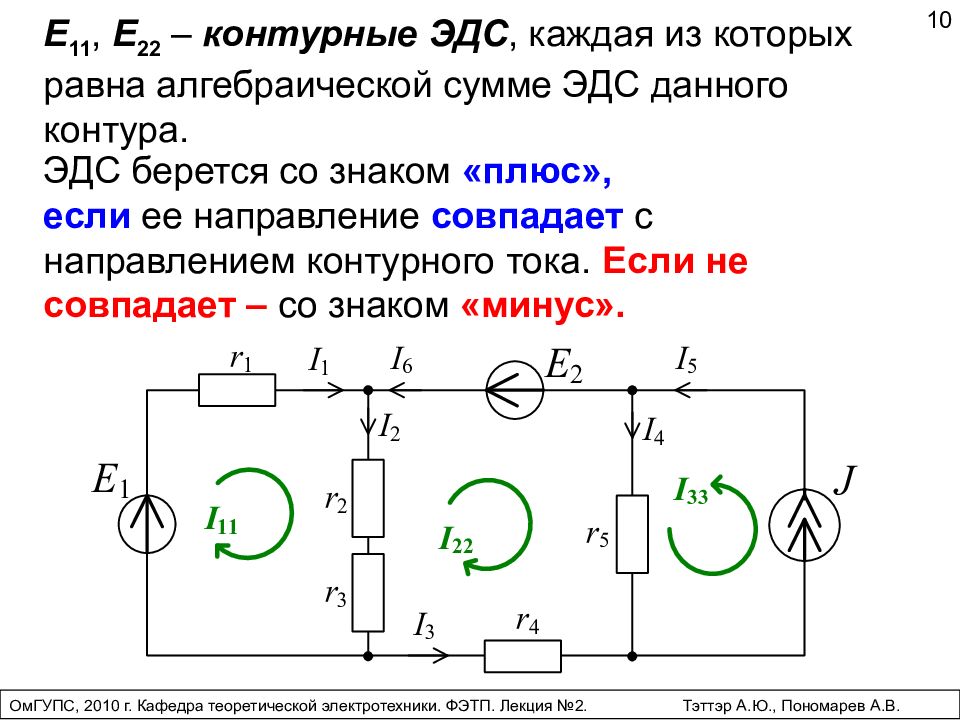
ЭДС берется со знаком «плюс», если ее направление совпадает с направлением контурного тока. Если не совпадает – со знаком «минус». 10 ОмГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция №2. Тэттэр А.Ю., Пономарев А.В. E 11, E 22 – контурные ЭДС, каждая из которых равна алгебраической сумме ЭДС данного контура.
Количество слагаемых в левой части уравнения равно числу независимых контуров. Последовательность определения токов ветвей методом контурных токов 11 ОмГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция №2. Тэттэр А.Ю., Пономарев А.В. Выбираются независимые контуры и направления контурных токов. Записывается система уравнений в общем виде. Число уравнений равно числу независимых контуров схемы минус число контуров, содержащих источники тока. !
Определяются токи ветвей. Последовательность определения токов ветвей методом контурных токов (продолжение) 12 ОмГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция №2. Тэттэр А.Ю., Пономарев А.В. Определяются коэффициенты при неизвестных – собственные и общие сопротивления контуров, а также контурные ЭДС. Рассчитываются контурные токи. Выбираются направления токов ветвей.
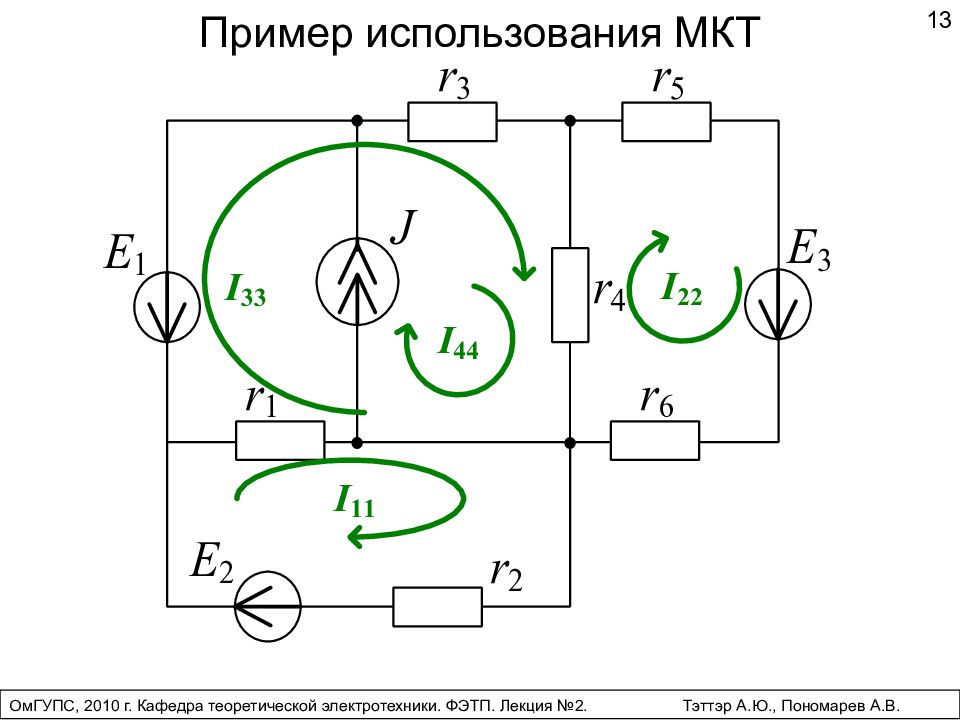
Пример использования МКТ 13 ОмГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция №2. Тэттэр А.Ю., Пономарев А.В.
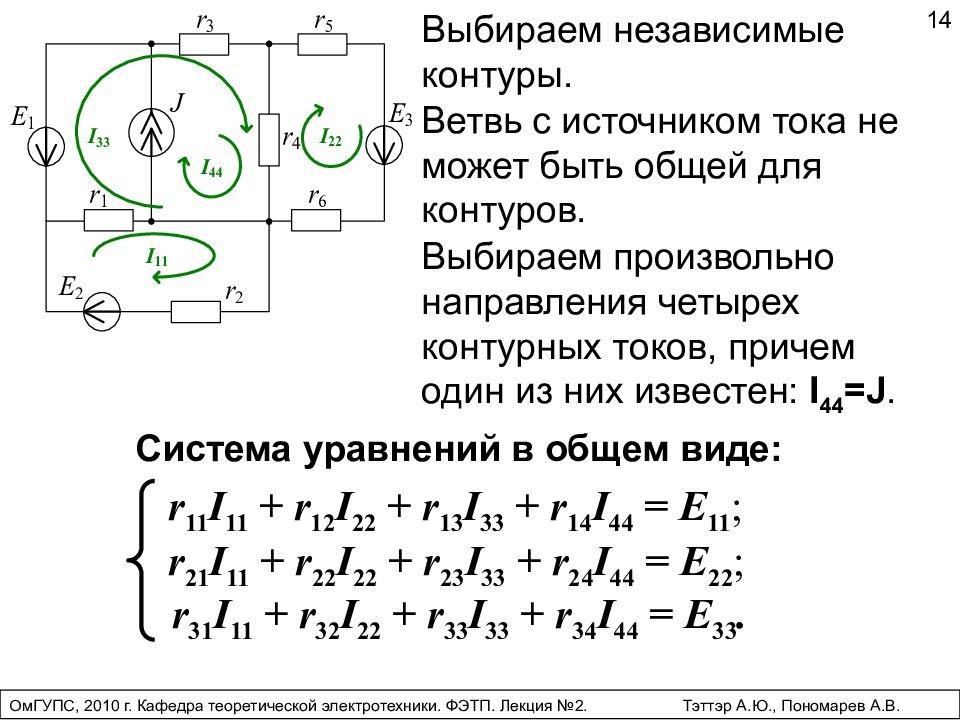
14 Выбираем произвольно направления четырех контурных токов, причем один из них известен: I 44 =J. Система уравнений в общем виде: r 11 I 11 + r 12 I 22 + r 13 I 33 + r 14 I 44 = E 11 ; r 21 I 11 + r 22 I 22 + r 23 I 33 + r 24 I 44 = E 22 ; r 31 I 11 + r 32 I 22 + r 33 I 33 + r 34 I 44 = E 33. ОмГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция №2. Тэттэр А.Ю., Пономарев А.В. Выбираем независимые контуры. Ветвь с источником тока не может быть общей для контуров.
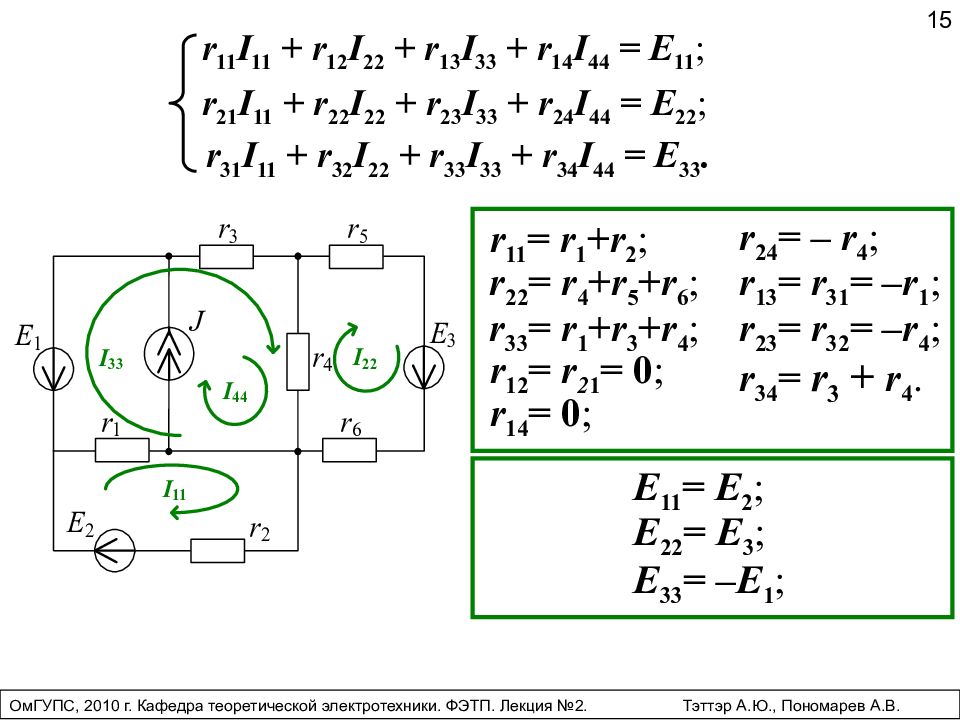
15 r 11 I 11 + r 12 I 22 + r 13 I 33 + r 14 I 44 = E 11 ; r 21 I 11 + r 22 I 22 + r 23 I 33 + r 24 I 44 = E 22 ; r 31 I 11 + r 32 I 22 + r 33 I 33 + r 34 I 44 = E 33. r 11 = r 1 + r 2 ; r 22 = r 4 + r 5 + r 6 ; r 33 = r 1 + r 3 + r 4 ; r 12 = r 2 1 = 0 ; r 14 = 0 ; r 24 = – r 4 ; E 11 = E 2 ; r 13 = r 31 = – r 1 ; r 23 = r 32 = – r 4 ; r 34 = r 3 + r 4. E 22 = E 3 ; E 33 = – E 1 ; ОмГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция №2. Тэттэр А.Ю., Пономарев А.В.
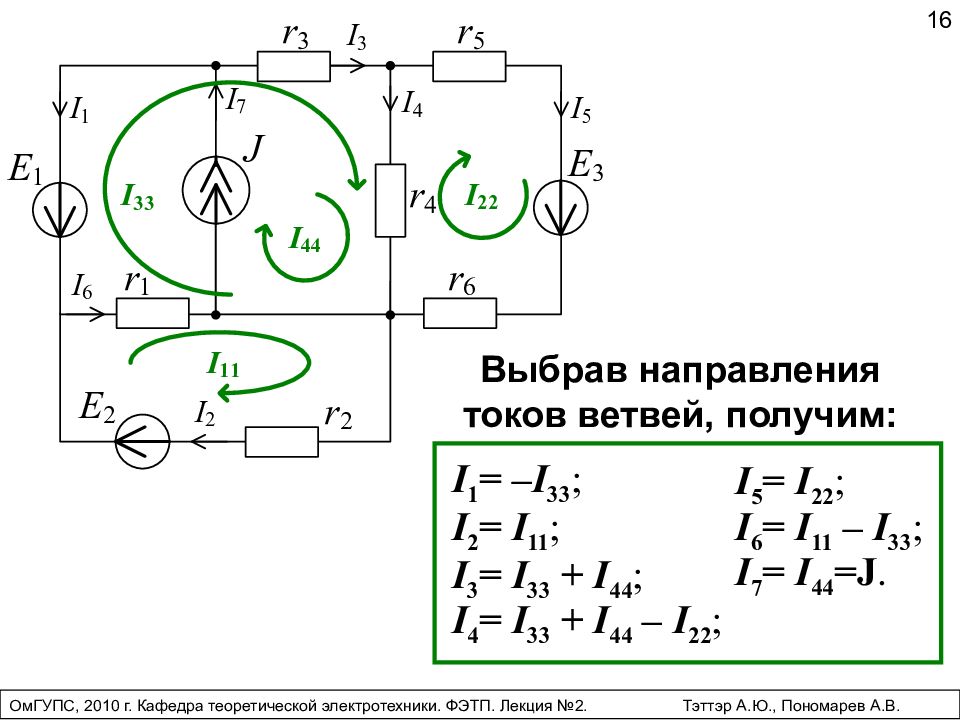
16 I 1 = – I 33 ; I 2 = I 11 ; I 3 = I 33 + I 44 ; I 5 = I 22 ; I 6 = I 11 – I 33 ; I 7 = I 44 = J. Выбрав направления токов ветвей, получим: I 4 = I 33 + I 44 – I 22 ; ОмГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция №2. Тэттэр А.Ю., Пономарев А.В.
Закон Ома для участка цепи с ЭДС 17 ОмГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция №2. Тэттэр А.Ю., Пономарев А.В.
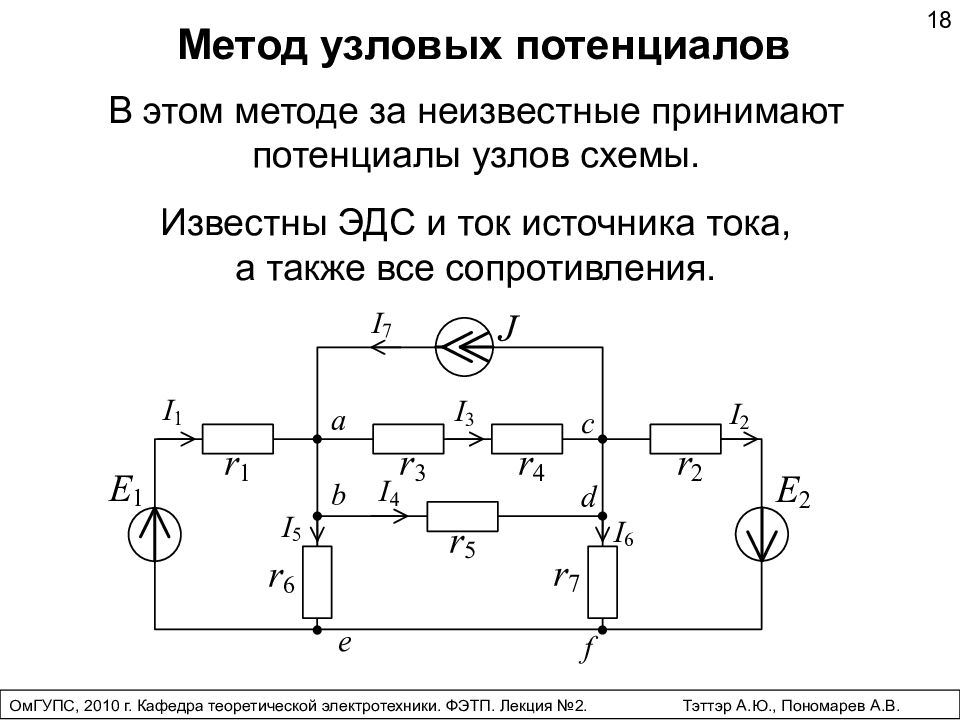
В этом методе за неизвестные принимают потенциалы узлов схемы. Метод узловых потенциалов 18 Известны ЭДС и ток источника тока, а также все сопротивления. ОмГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция №2. Тэттэр А.Ю., Пономарев А.В.
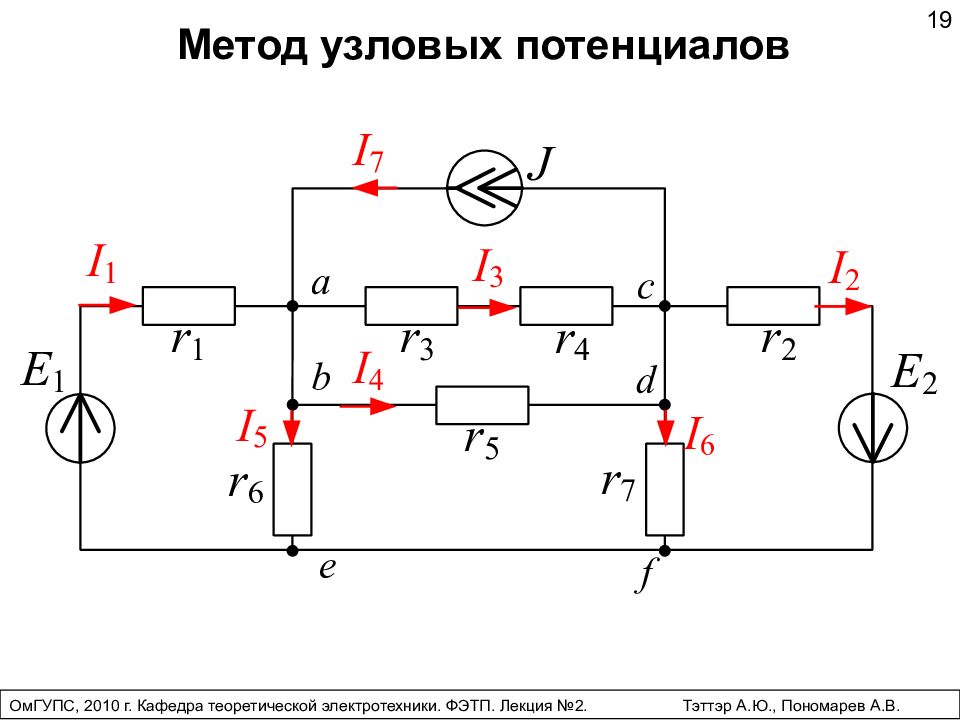
Метод узловых потенциалов 19 ОмГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция №2. Тэттэр А.Ю., Пономарев А.В.
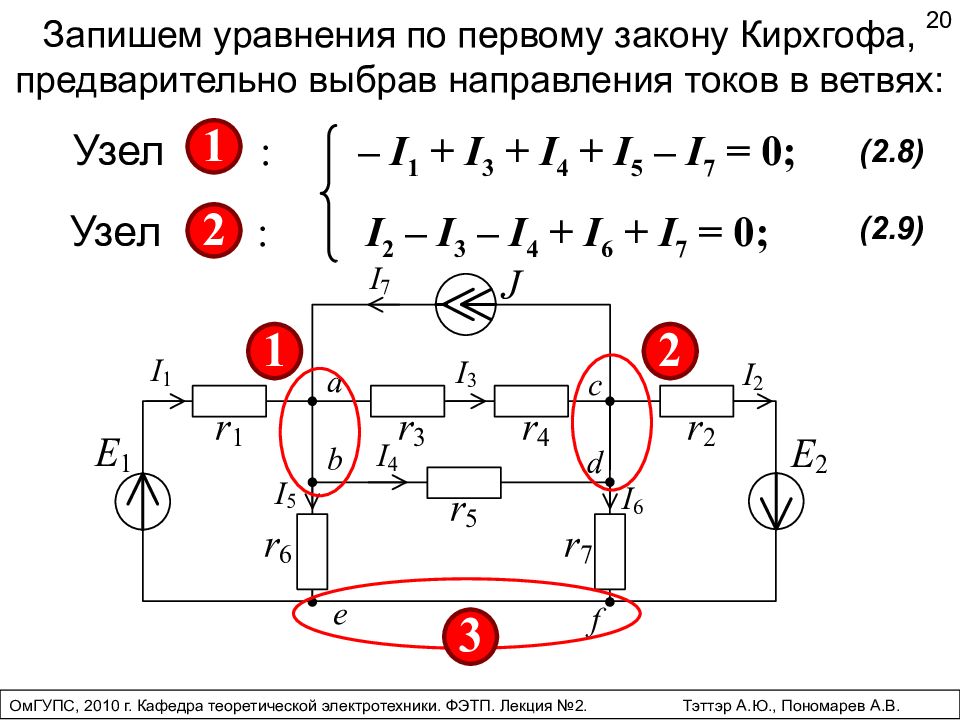
Запишем уравнения по первому закону Кирхгофа, предварительно выбрав направления токов в ветвях: 20 Узел : – I 1 + I 3 + I 4 + I 5 – I 7 = 0; ( 2.8 ) Узел : I 2 – I 3 – I 4 + I 6 + I 7 = 0; ( 2.9 ) ОмГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция №2. Тэттэр А.Ю., Пономарев А.В.
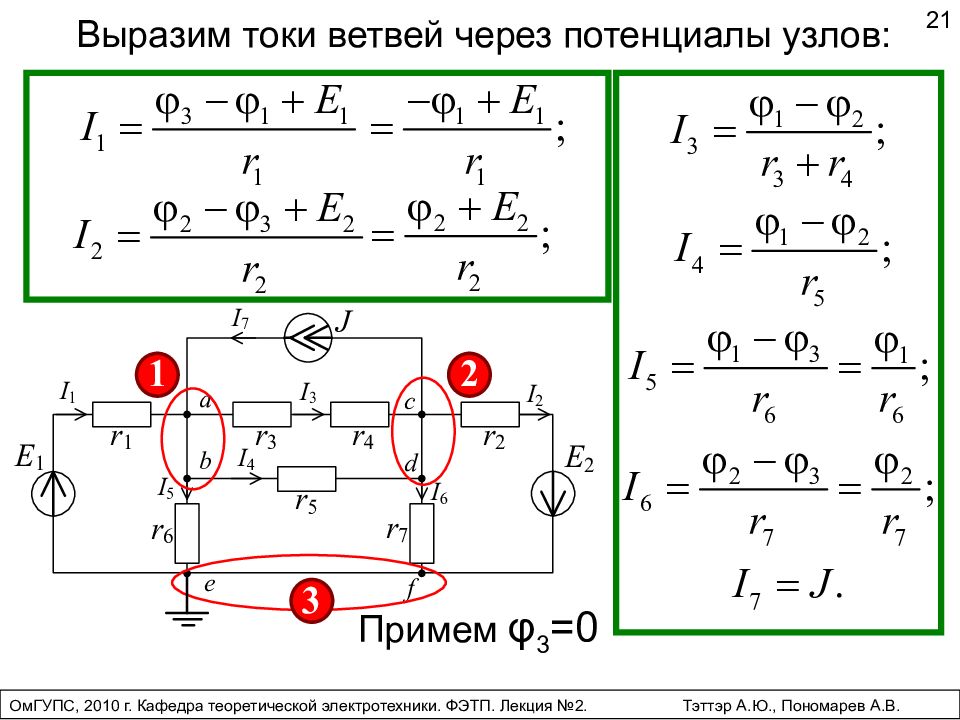
Выразим токи ветвей через потенциалы узлов: 21 Примем φ 3 =0 ОмГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция №2. Тэттэр А.Ю., Пономарев А.В.
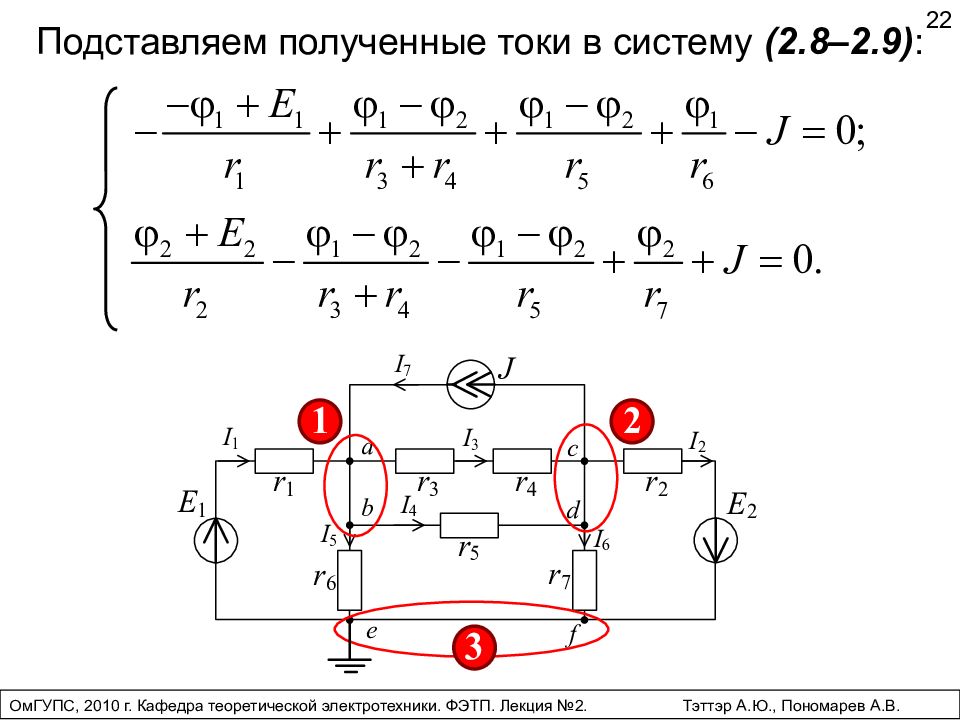
Подставляем полученные токи в систему ( 2.8–2.9) : 22 ОмГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция №2. Тэттэр А.Ю., Пономарев А.В.
После группировки получим: 23 ОмГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция №2. Тэттэр А.Ю., Пономарев А.В. В общем виде:
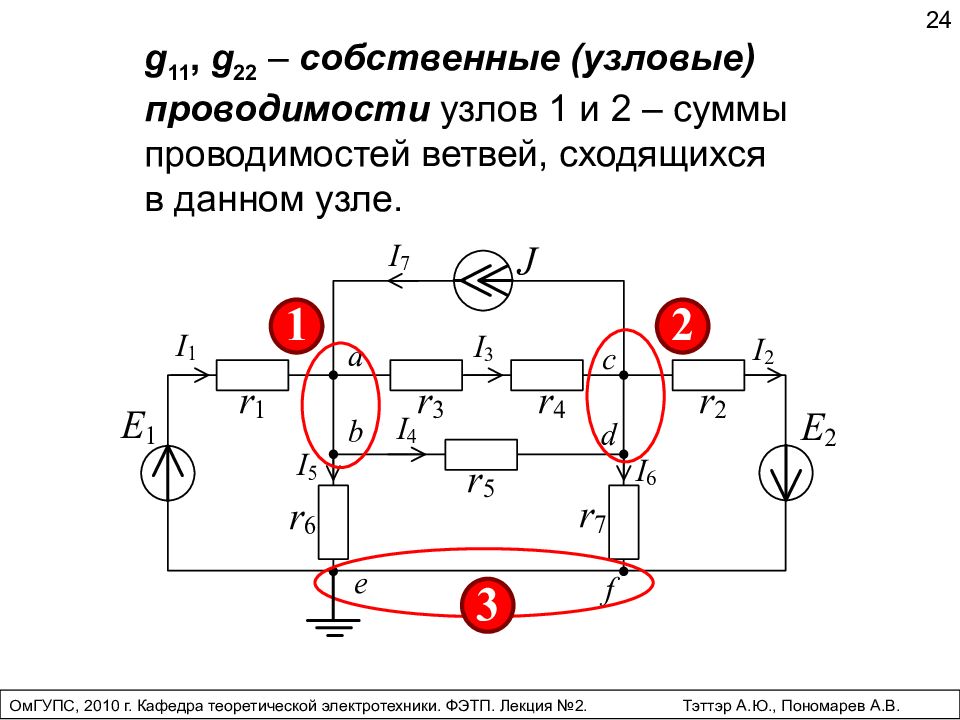
g 11, g 22 – собственные (узловые) проводимости узлов 1 и 2 – суммы проводимостей ветвей, сходящихся в данном узле. 24 ОмГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция №2. Тэттэр А.Ю., Пономарев А.В.
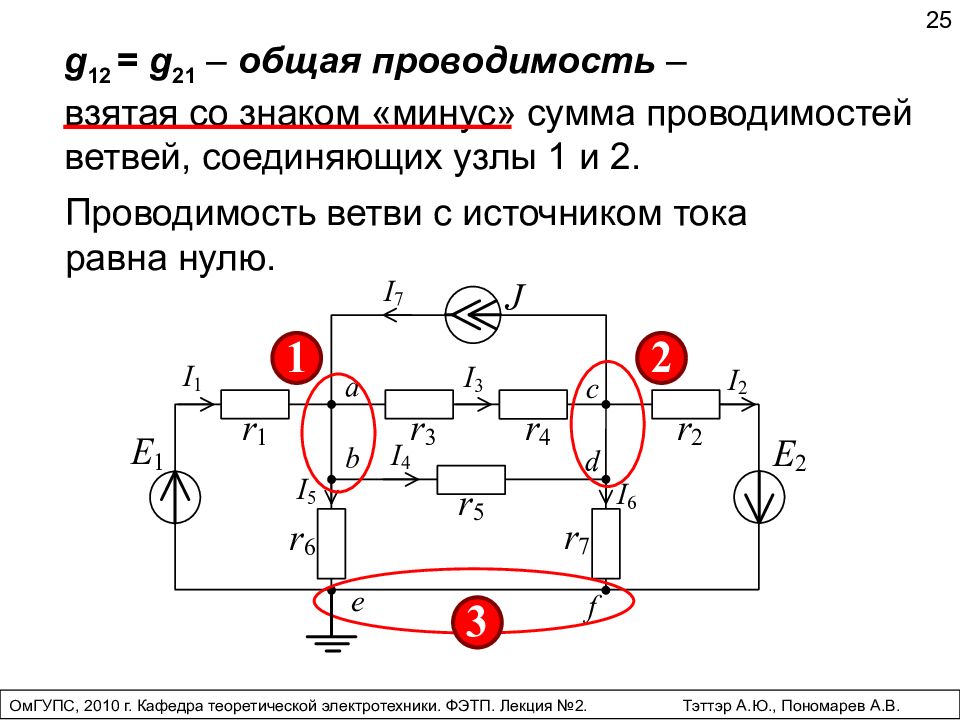
g 1 2 = g 2 1 – общая проводимость – взятая со знаком «минус» сумма проводимостей ветвей, соединяющих узлы 1 и 2. 25 ОмГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция №2. Тэттэр А.Ю., Пономарев А.В. Проводимость ветви с источником тока равна нулю.
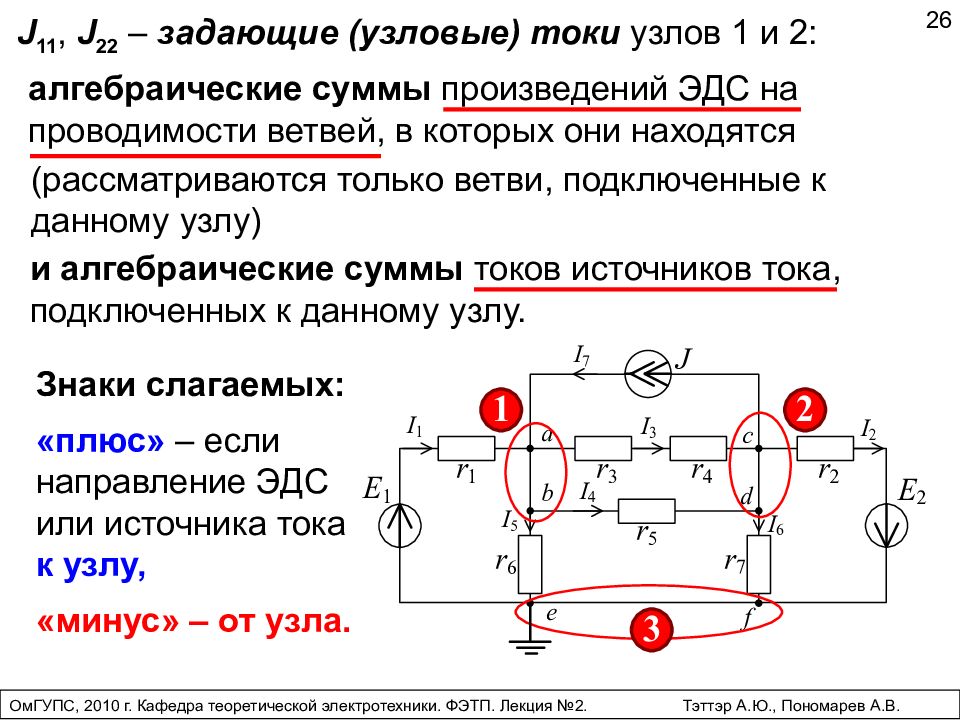
J 11, J 22 – задающие (узловые) токи узлов 1 и 2: 26 ОмГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция №2. Тэттэр А.Ю., Пономарев А.В. Знаки слагаемых: «плюс» – если направление ЭДС или источника тока к узлу, «минус» – от узла. алгебраические суммы произведений ЭДС на проводимости ветвей, в которых они находятся (рассматриваются только ветви, подключенные к данному узлу) и алгебраические суммы токов источников тока, подключенных к данному узлу.
Число уравнений системы на единицу меньше числа узлов схемы. Последовательность определения токов ветвей методом узловых потенциалов: 27 ОмГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция №2. Тэттэр А.Ю., Пономарев А.В. Записывается система уравнений в общем виде. Если в схеме содержится ветвь с источником ЭДС без сопротивлений, то φ 2 = φ 1 + Е. Приняв φ 1, равным 0, получим φ 2 = Е. ! Уравнение для φ 2 – убирается!
Рассчитываются потенциалы узлов. Последовательность определения токов ветвей методом узловых потенциалов: (продолжение) 28 ОмГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция №2. Тэттэр А.Ю., Пономарев А.В. Определяются коэффициенты при неизвестных – собственные и общие проводимости, а также задающие токи узлов. Выбираются направления токов ветвей. Определяются токи ветвей.
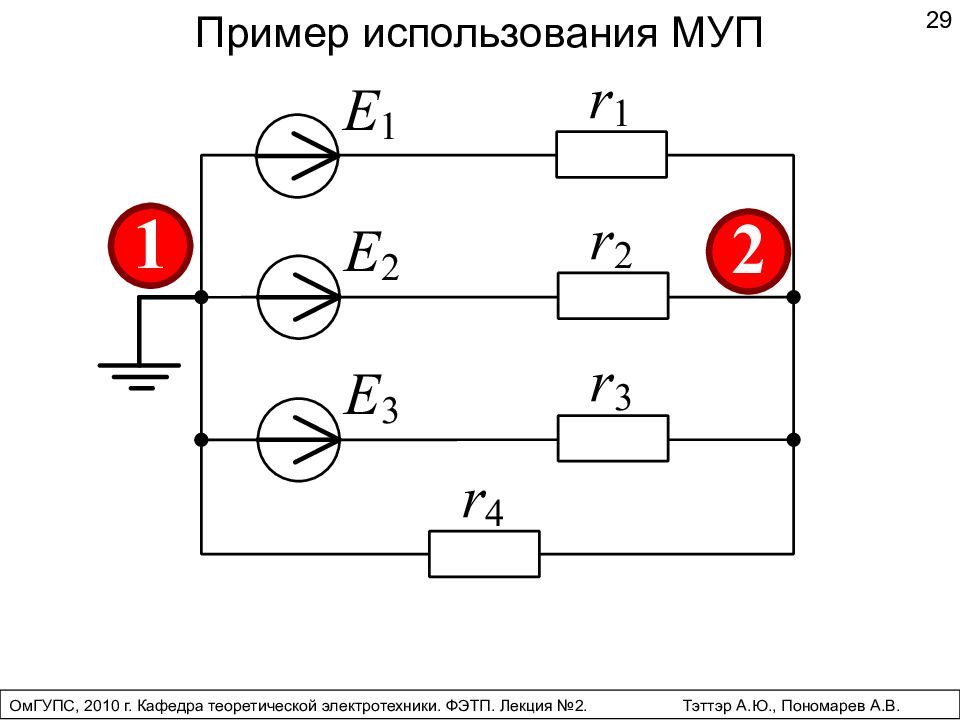
Пример использования МУП 29 ОмГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция №2. Тэттэр А.Ю., Пономарев А.В.
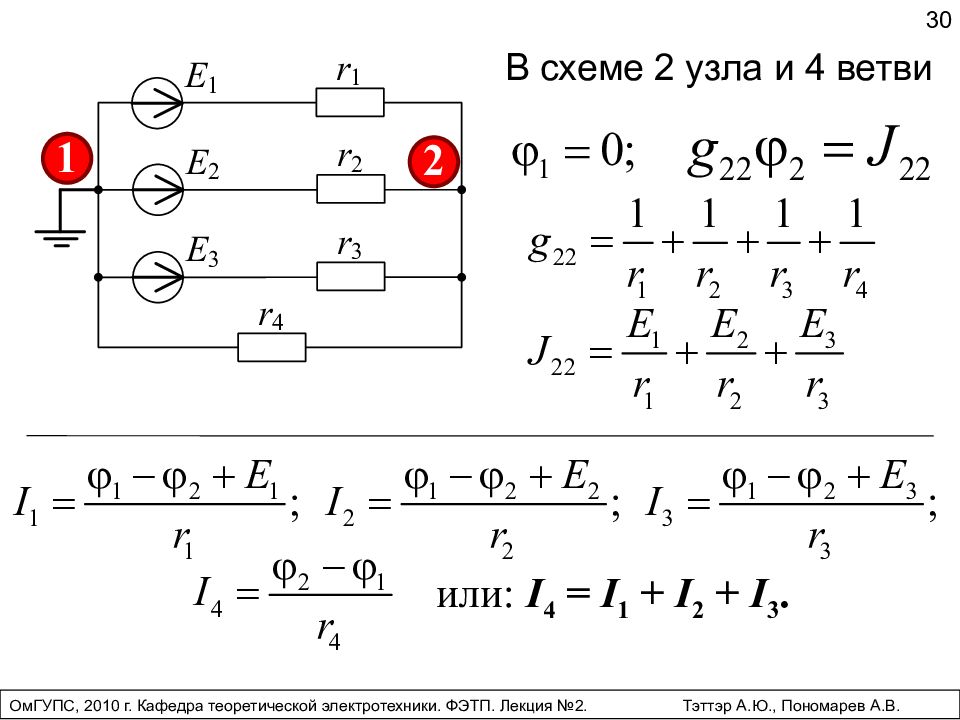
30 В схеме 2 узла и 4 ветви или: I 4 = I 1 + I 2 + I 3. ОмГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция №2. Тэттэр А.Ю., Пономарев А.В.
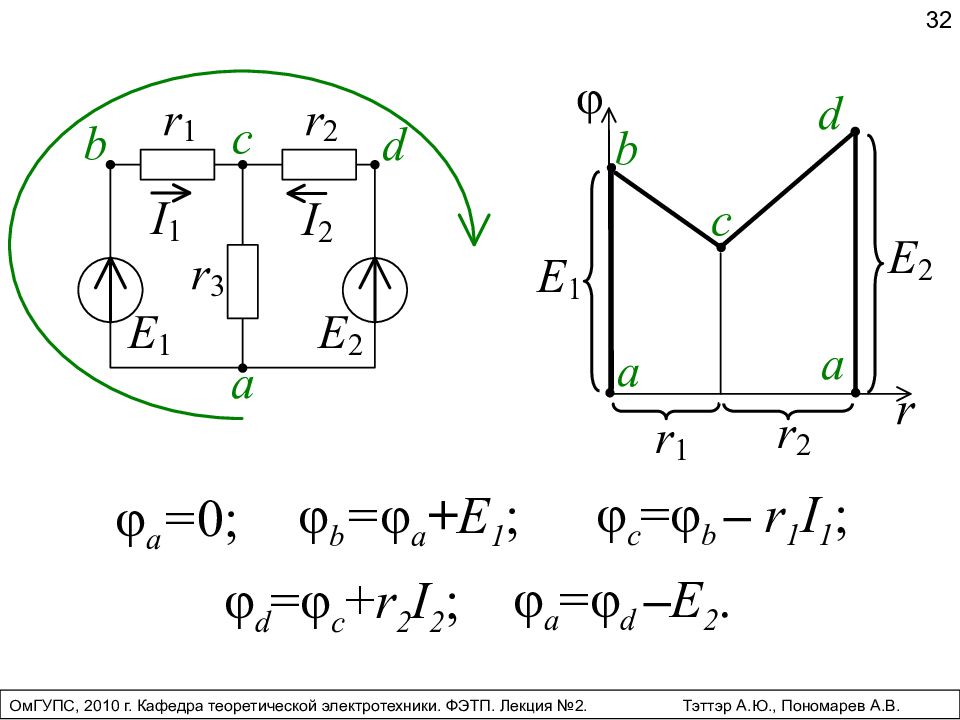
31 Потенциальная диаграмма – график распределения потенциала вдоль участка цепи или контура. По оси ординат откладывают потенциалы. По оси абсцисс – сопротивления. ОмГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция №2. Тэттэр А.Ю., Пономарев А.В.
32 φ a = 0; ОмГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция №2. Тэттэр А.Ю., Пономарев А.В. φ a = φ d – E 2. φ b = φ a + E 1 ; φ c = φ b – r 1 I 1 ; φ d = φ c + r 2 I 2 ;
33 Баланс мощностей ОмГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция №2. Тэттэр А.Ю., Пономарев А.В. На основании закона сохранения энергии мощность, потребляемая в электрической цепи, должна быть равна мощности, поставляемой источниками. Уравнение баланса мощностей имеет вид: или
34 Определение знаков слагаемых: a б в ОмГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция №2. Тэттэр А.Ю., Пономарев А.В.
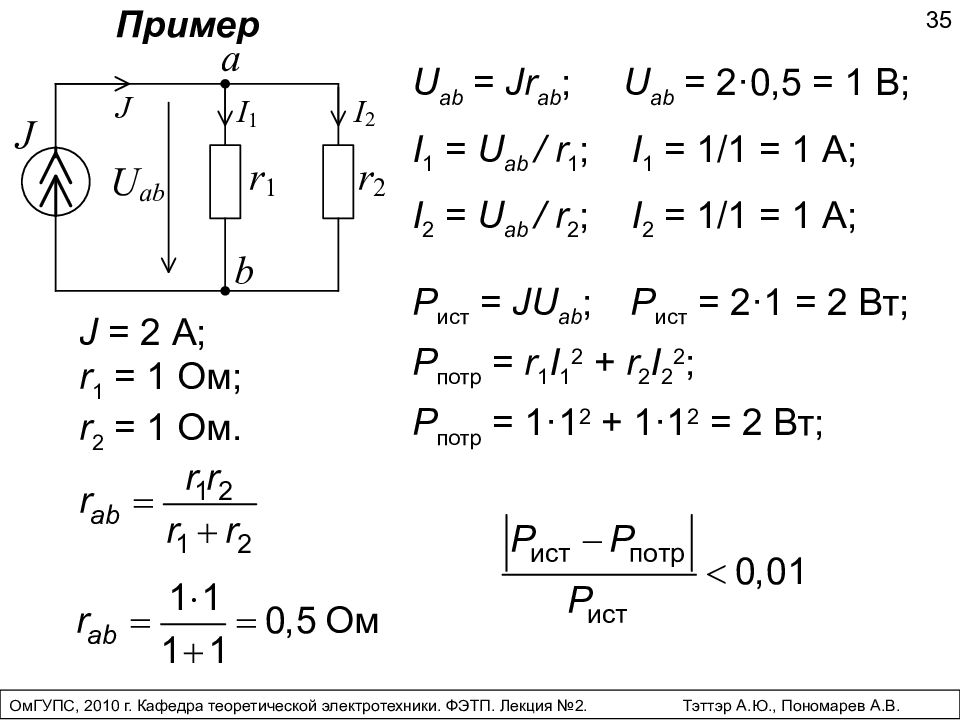
35 Пример J = 2 А; r 1 = 1 Ом; r 2 = 1 Ом. U ab = Jr ab ; U ab = 2 ·0,5 = 1 В; I 1 = U ab / r 1 ; I 1 = 1/1 = 1 А; I 2 = U ab / r 2 ; I 2 = 1/1 = 1 А; P ист = JU ab ; P ист = 2 · 1 = 2 Вт; P потр = r 1 I 1 2 + r 2 I 2 2 ; P потр = 1 · 1 2 + 1 · 1 2 = 2 Вт; ОмГУПС, 2010 г. Кафедра теоретической электротехники. ФЭТП. Лекция №2. Тэттэр А.Ю., Пономарев А.В.
