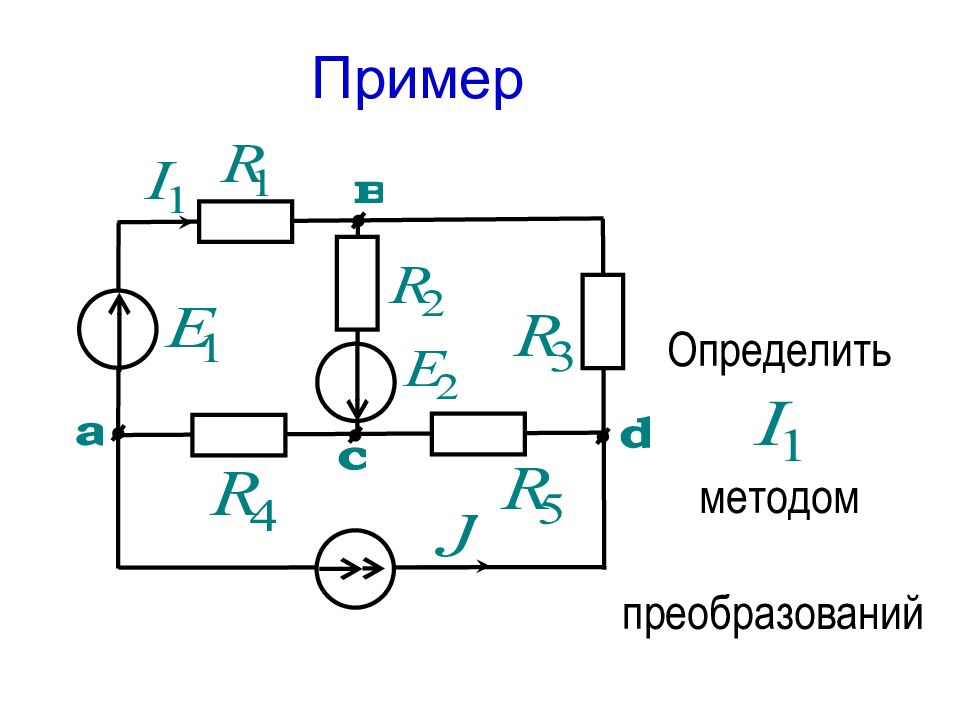
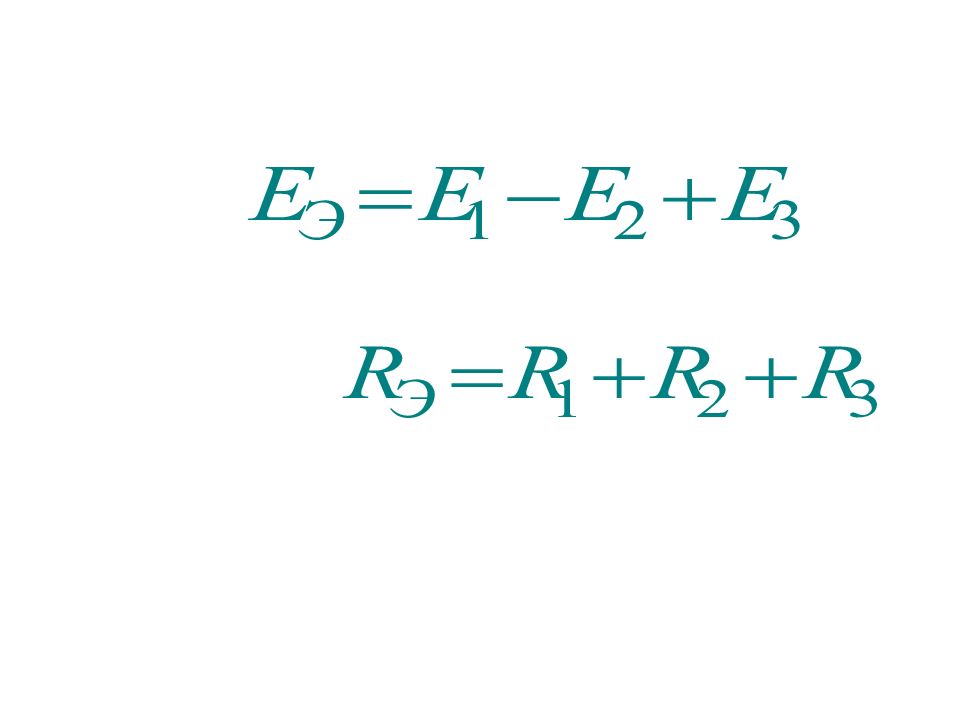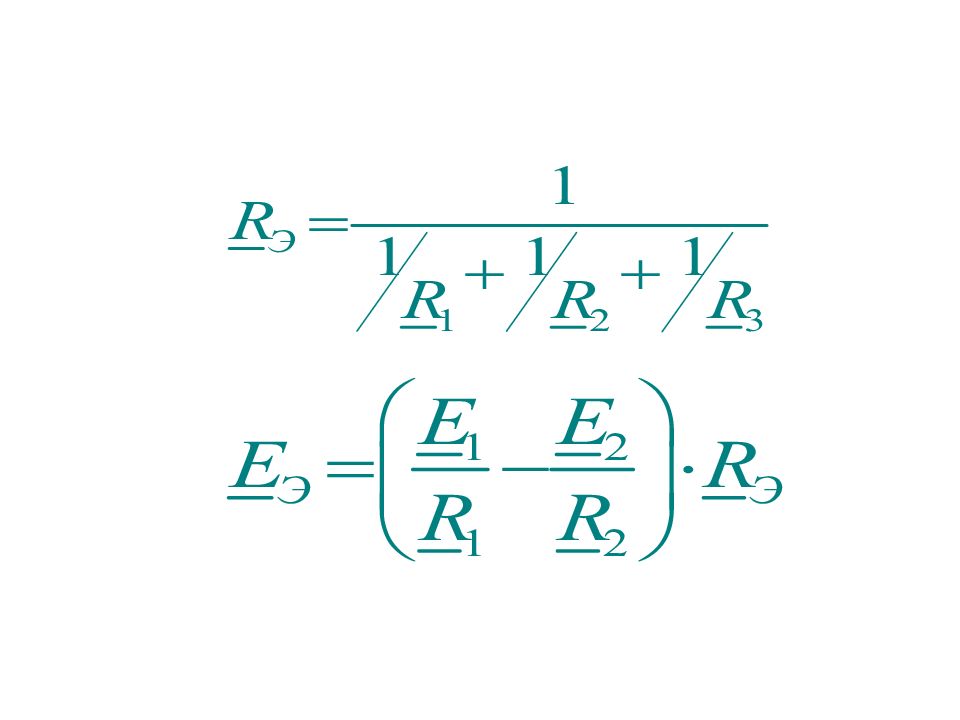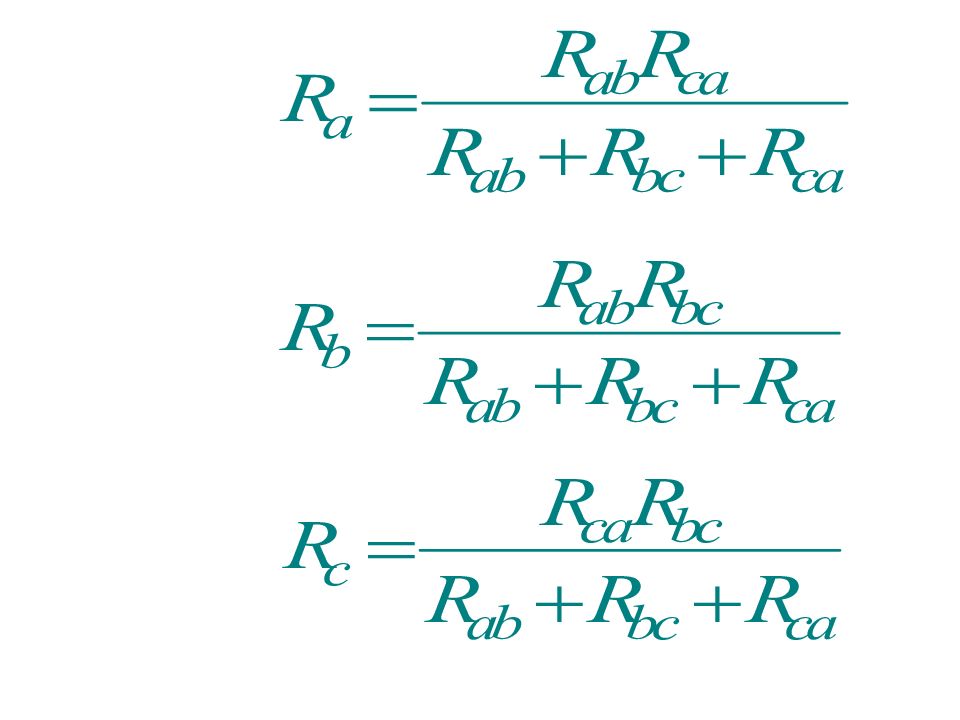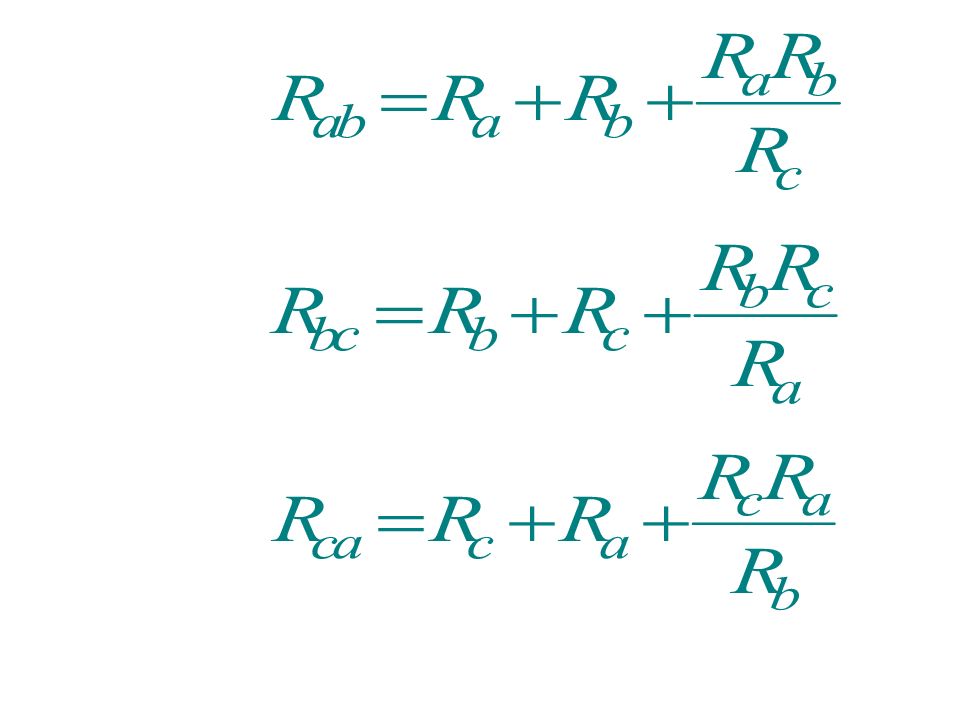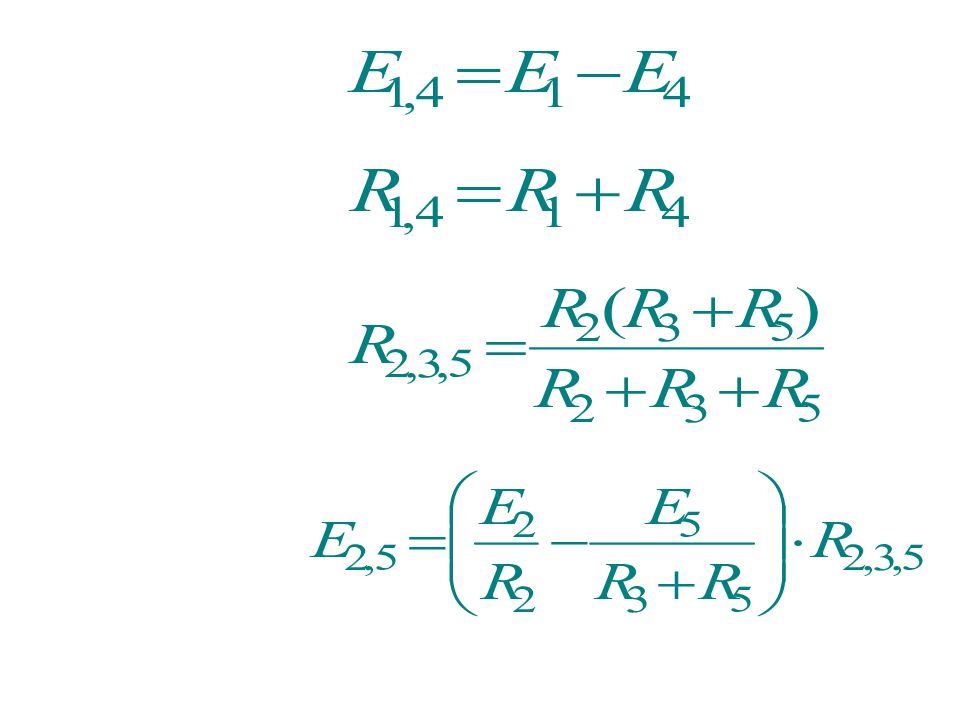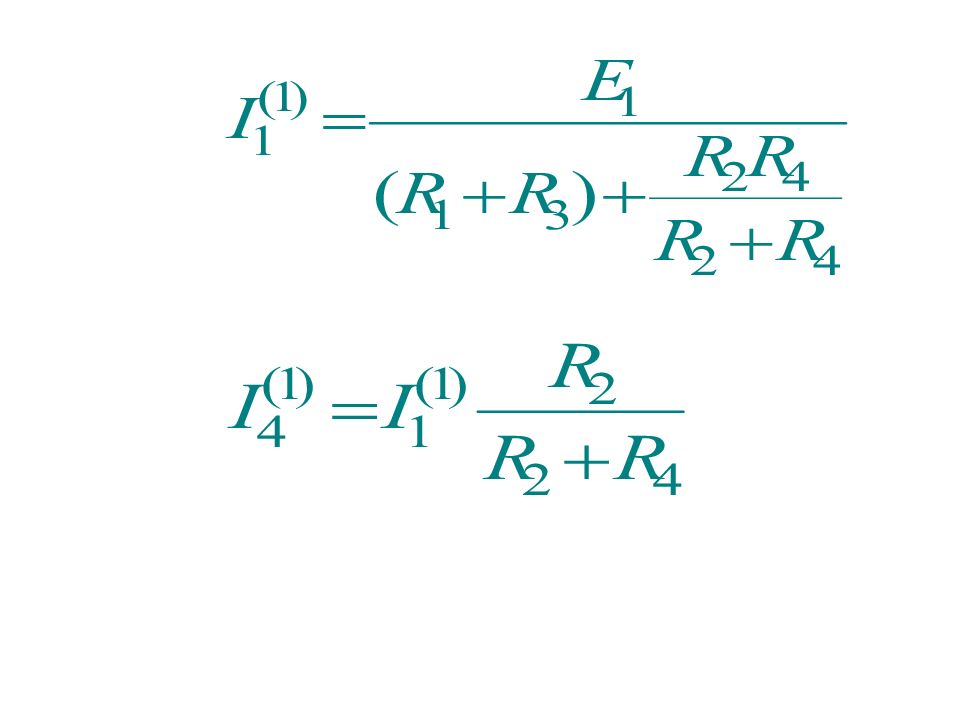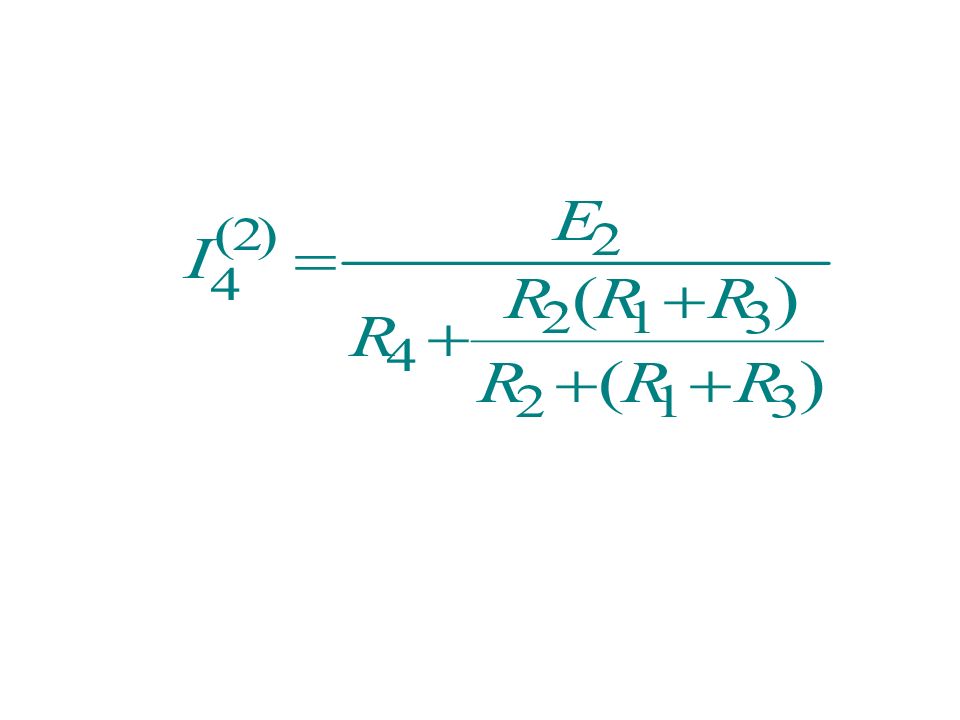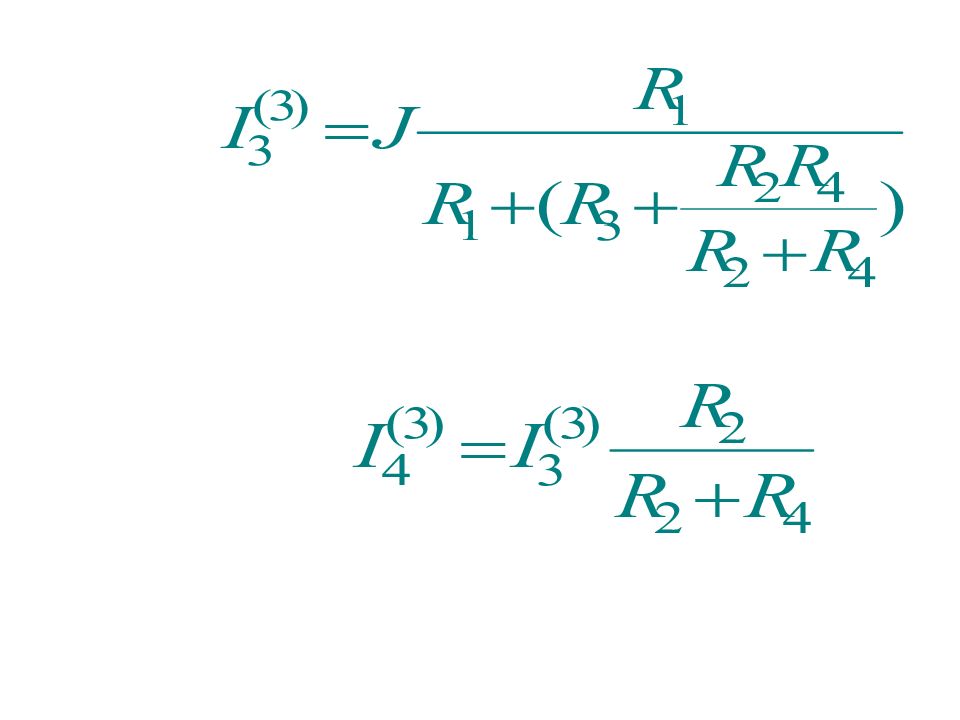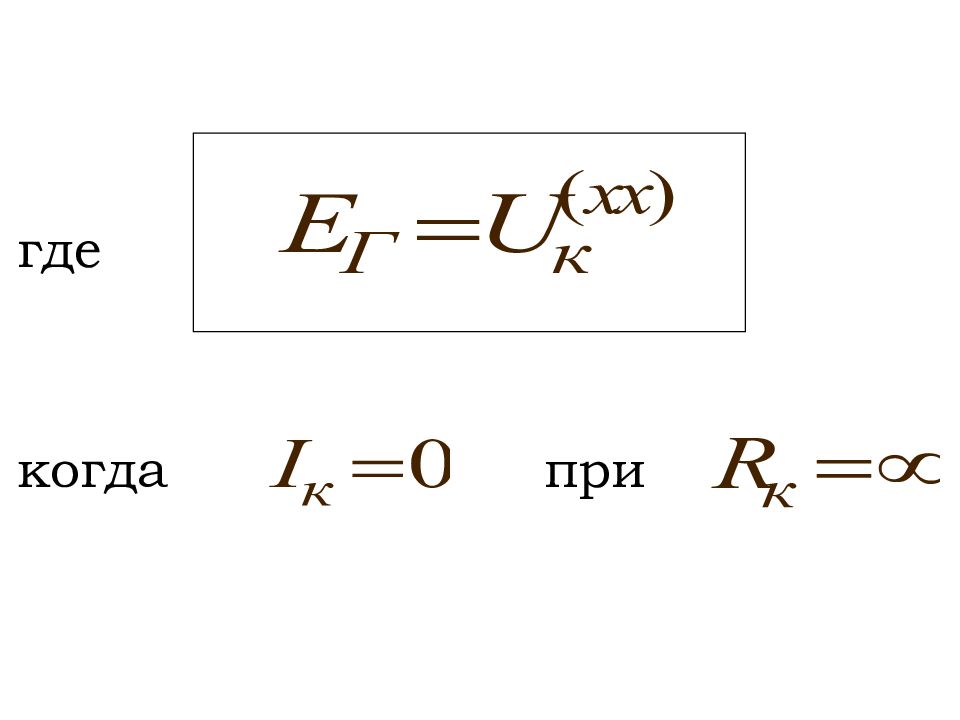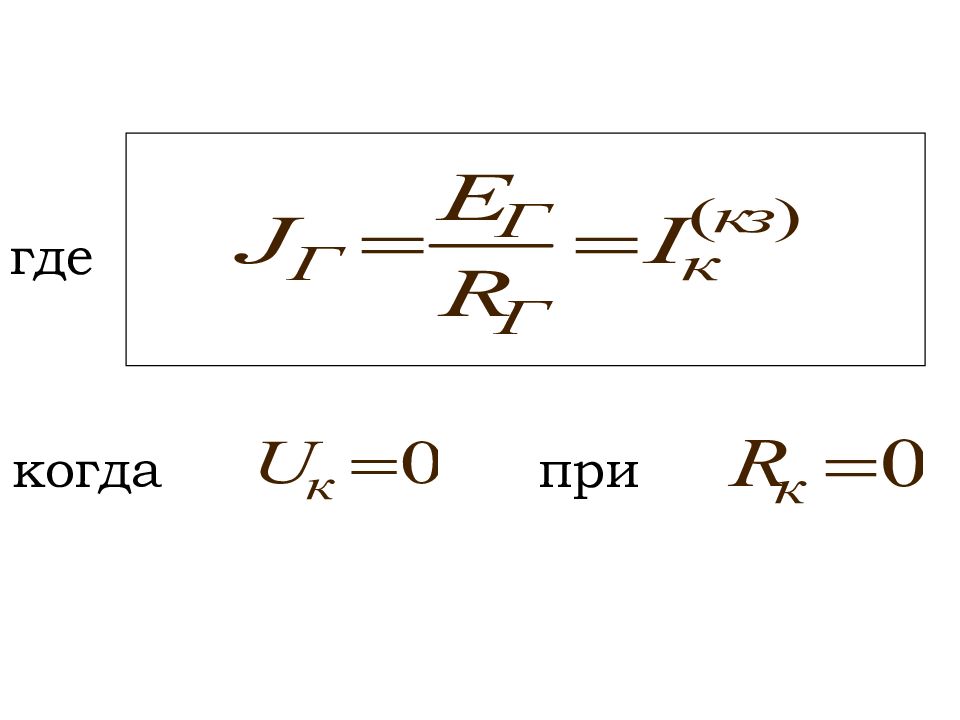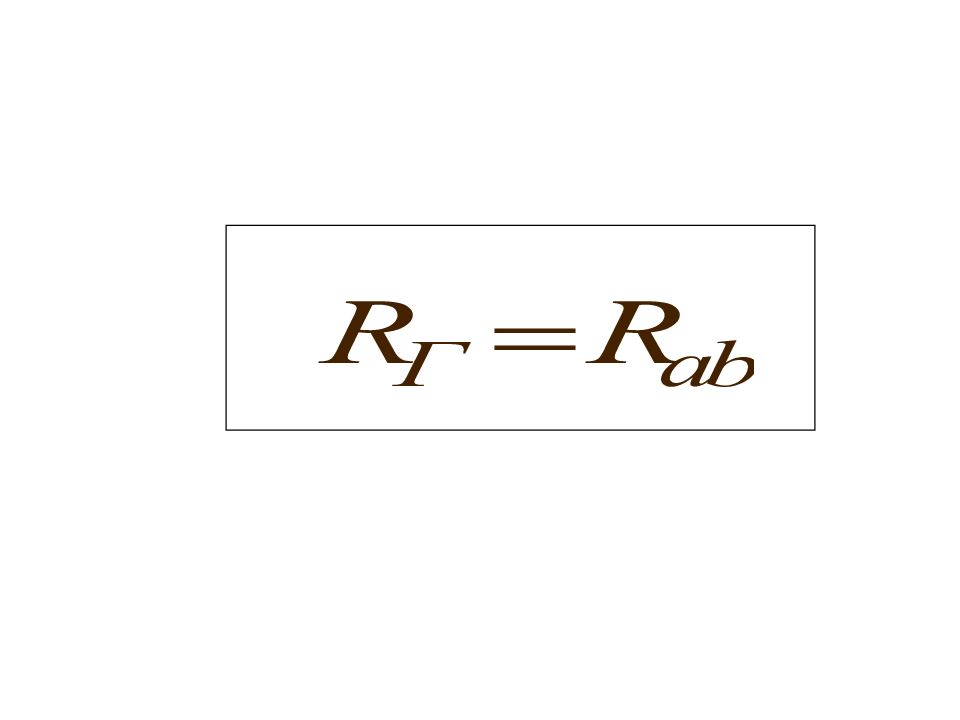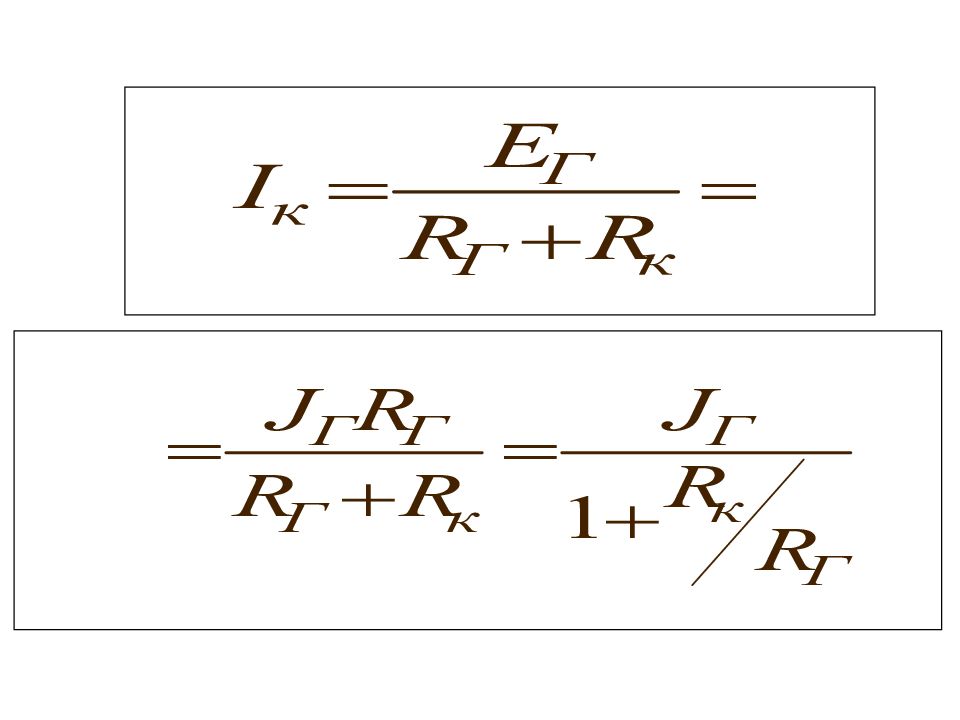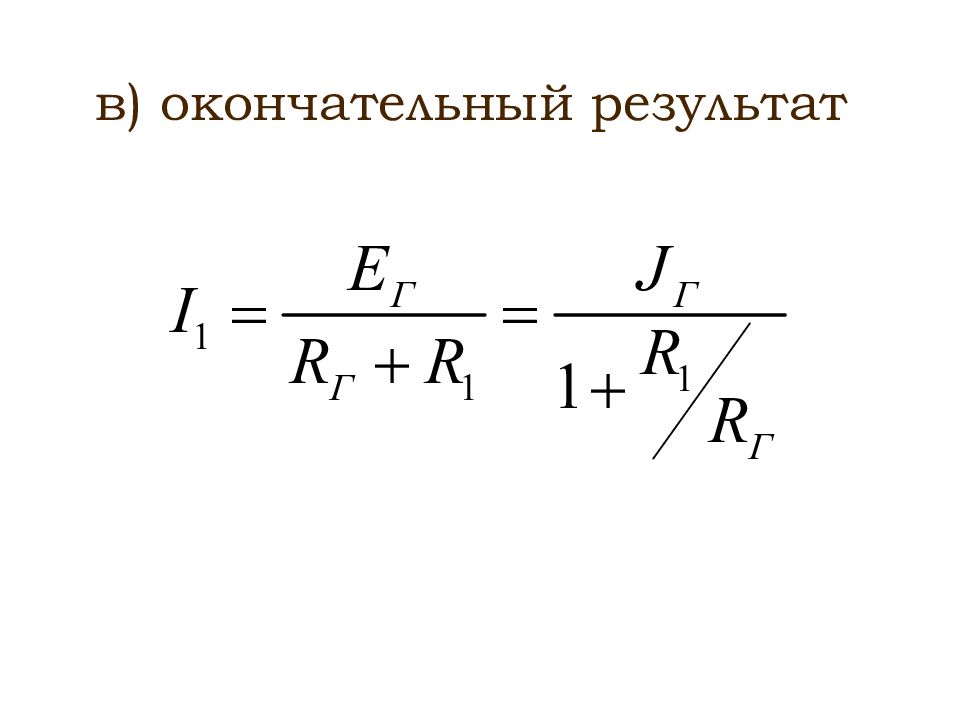Первый слайд презентации: Лекция 4 МЕТОД ЭКВИВАЛЕНТНЫХ ПРЕОБРАЗОВАНИЙ
Слайд 2
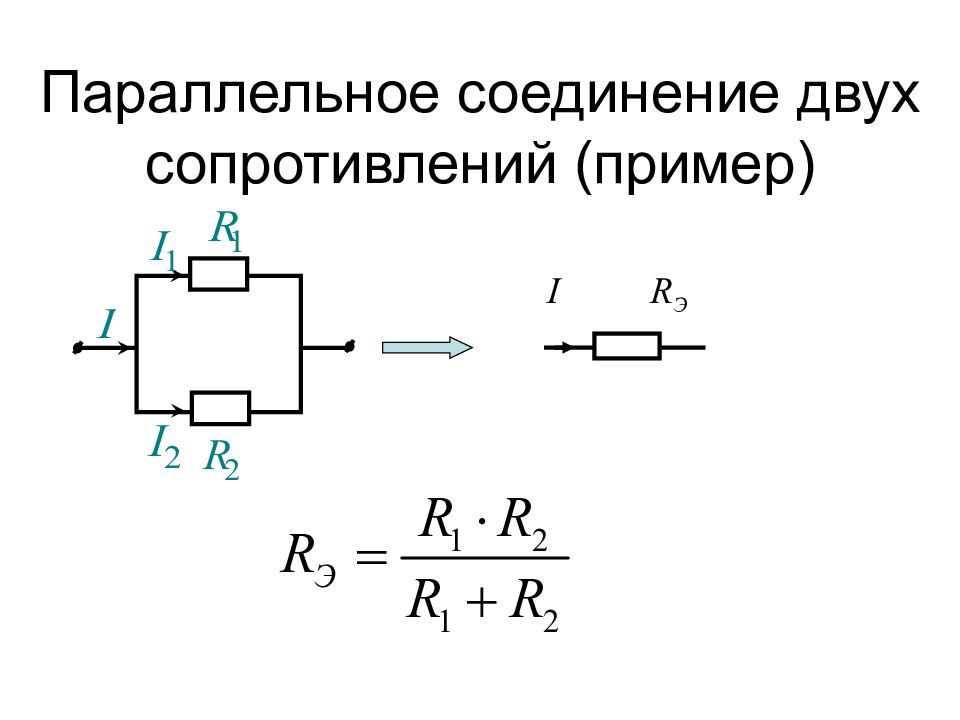
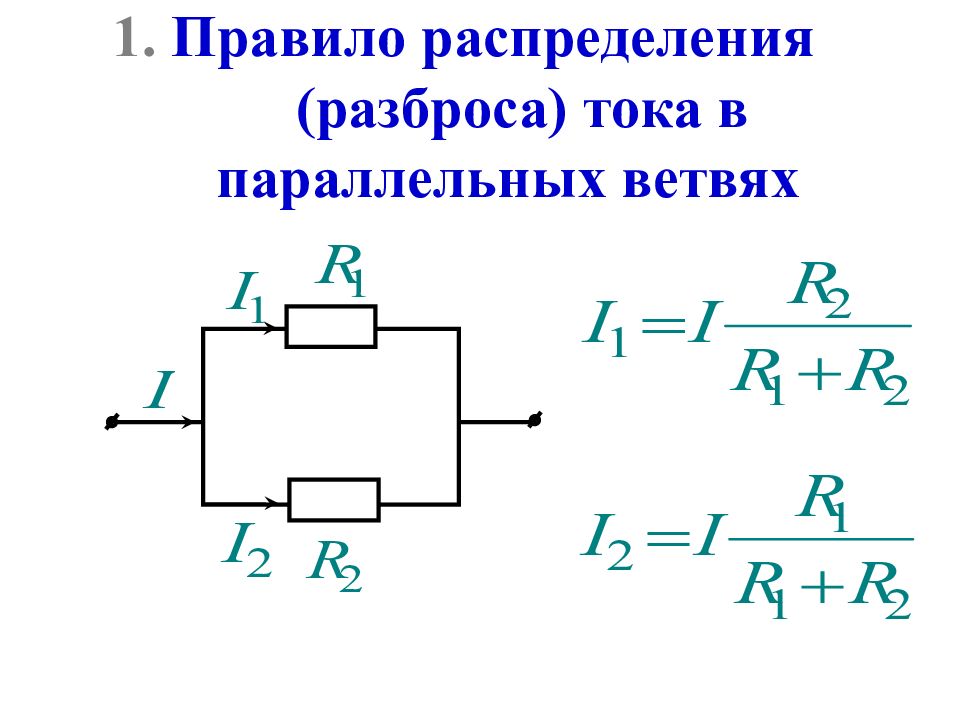
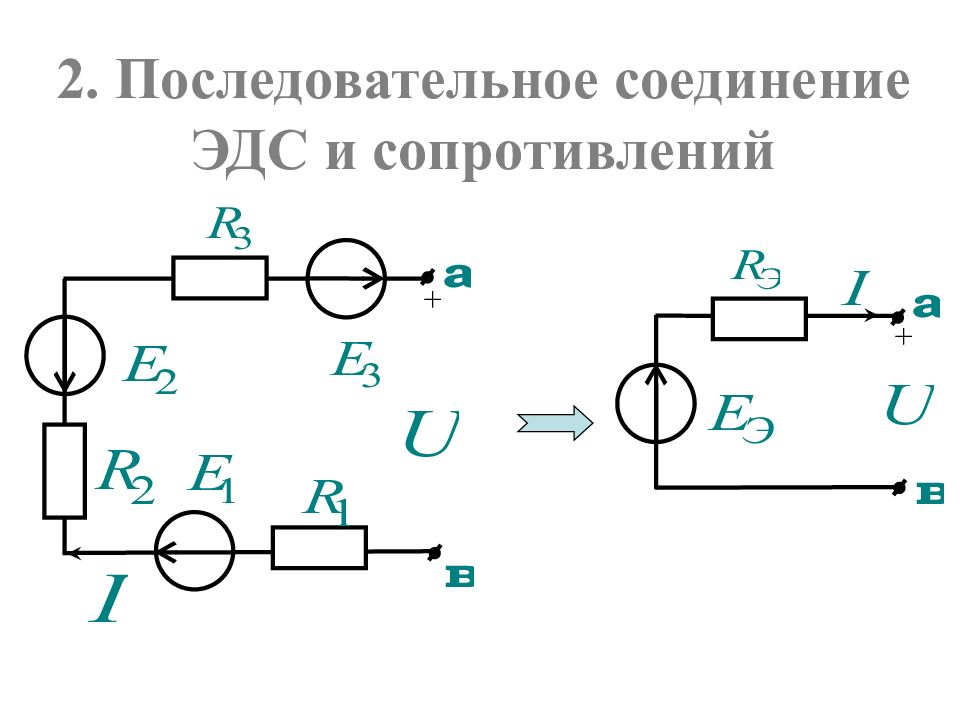
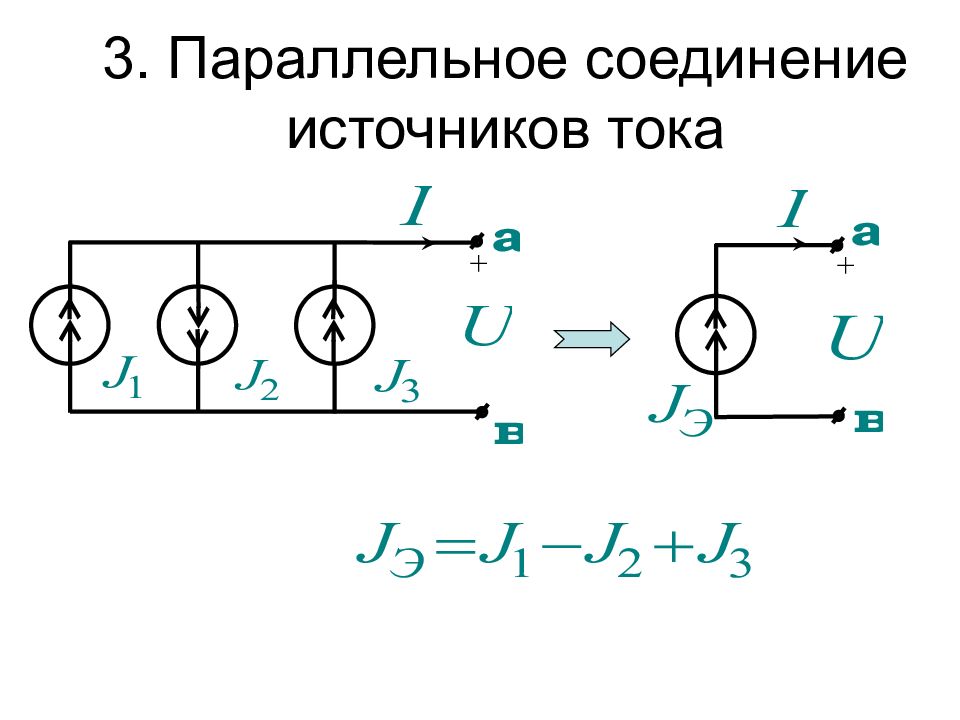
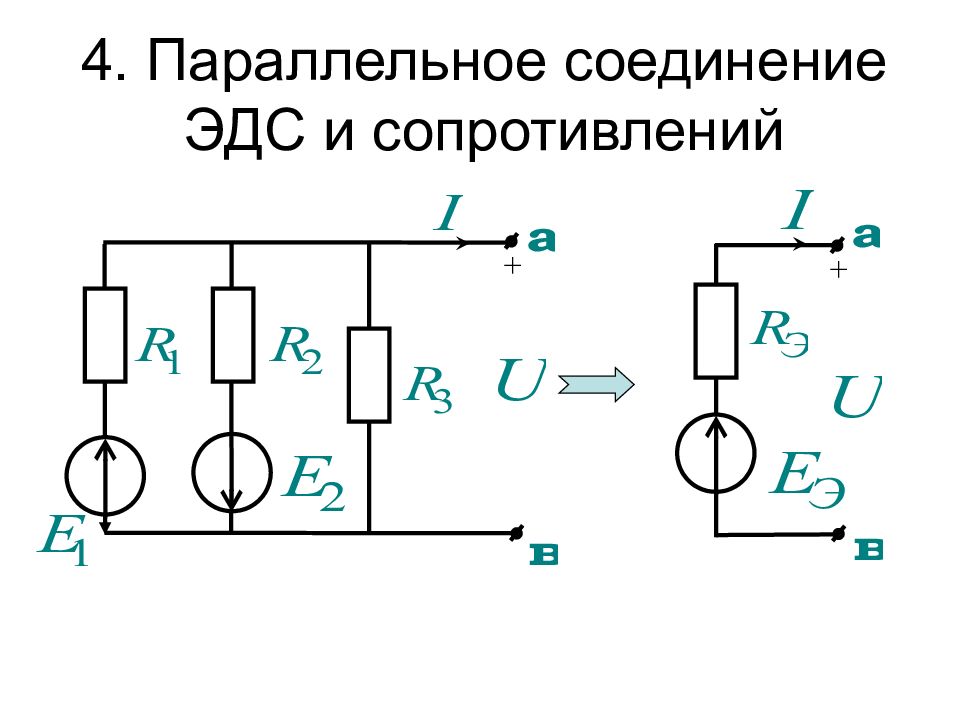
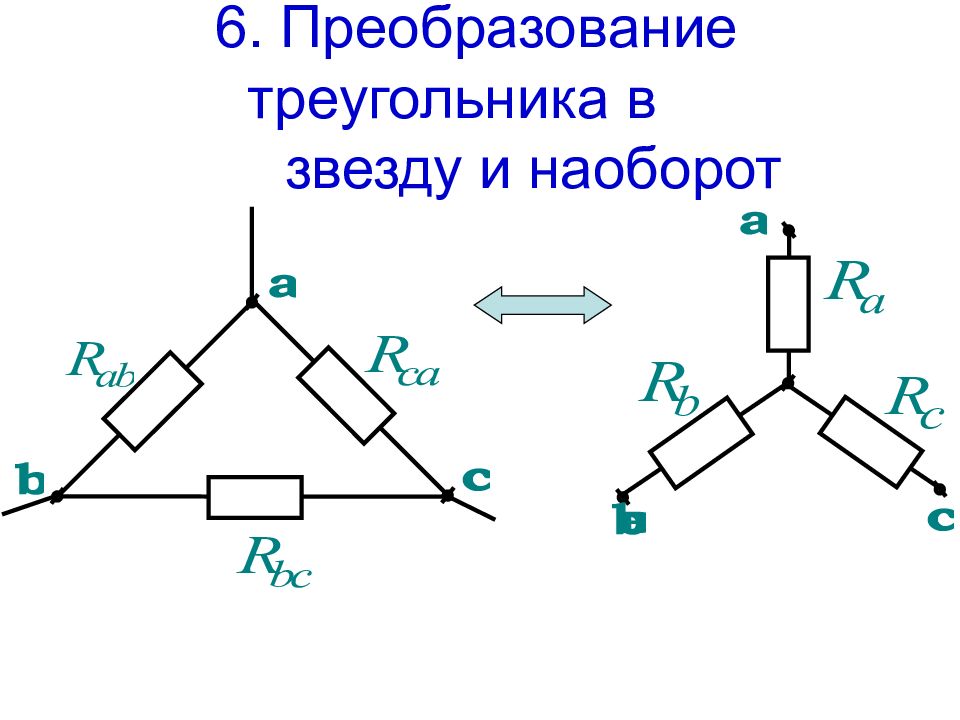
Преобразования схем используются для их упрощения и могут быть доказаны при помощи законов Ома и Кирхгофа. Приведем правила преобразований без доказательства
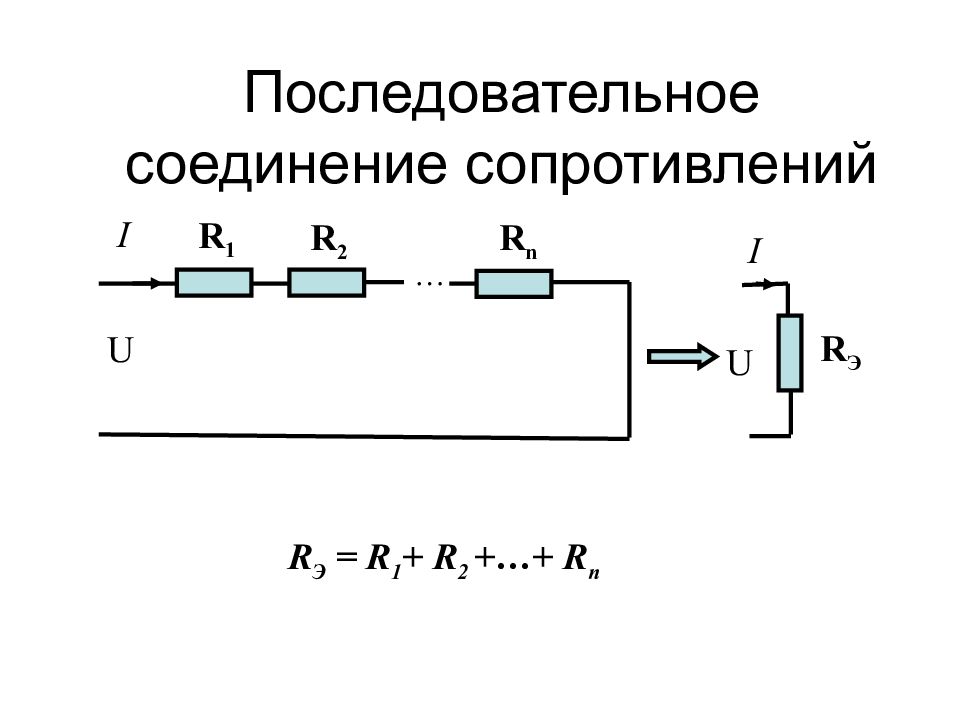
Слайд 3: Последовательное соединение сопротивлений
R Э = R 1 + R 2 +…+ R n R 1 R 2 R n U I U R Э I …
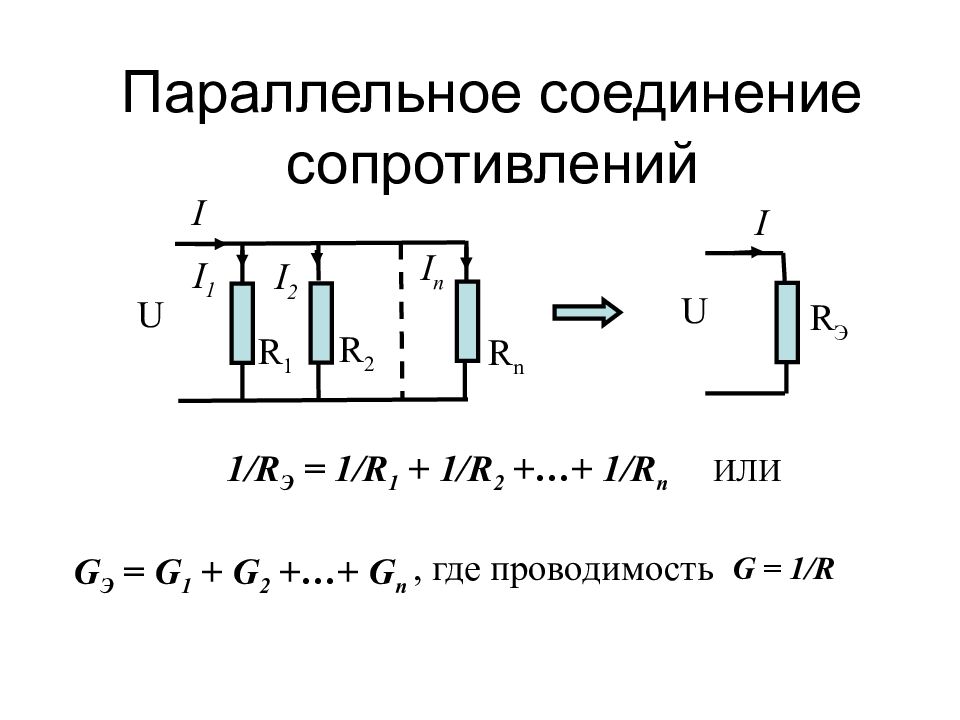
Слайд 4: Параллельное соединение сопротивлений
R n R 2 R 1 R Э I I 1 I 2 I n U U I 1/R Э = 1/ R 1 + 1/R 2 +…+ 1/R n ИЛИ G Э = G 1 + G 2 +…+ G n G = 1/R , где проводимость
Слайд 12: Метод узловых напряжений
Е К = I К R+U AB I K = (E K - U AB )/R K = (E K - U AB )G K
Слайд 20
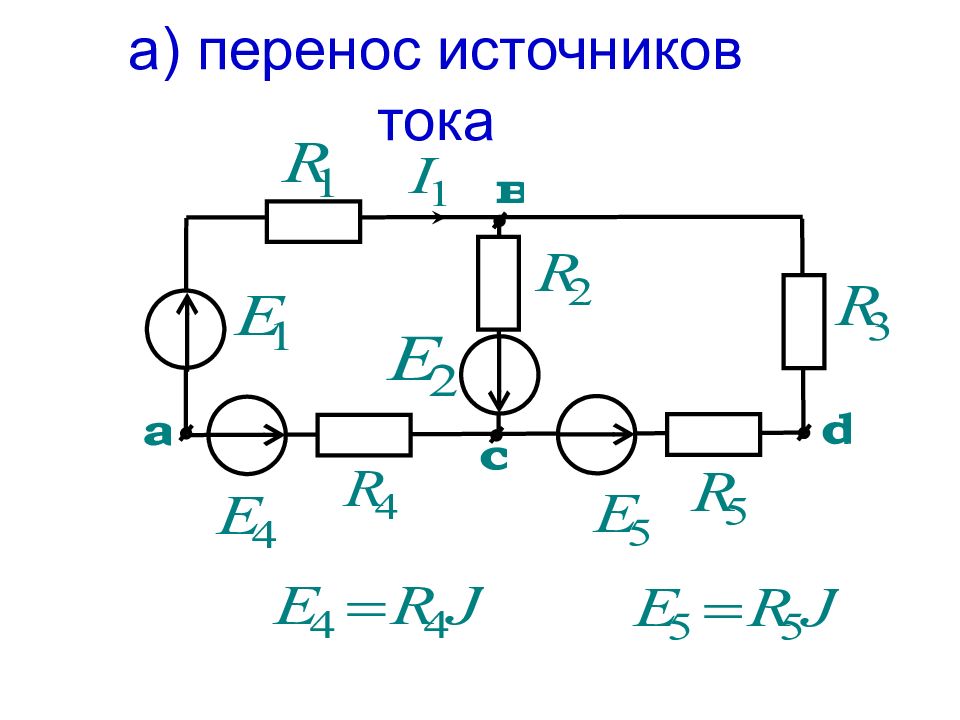
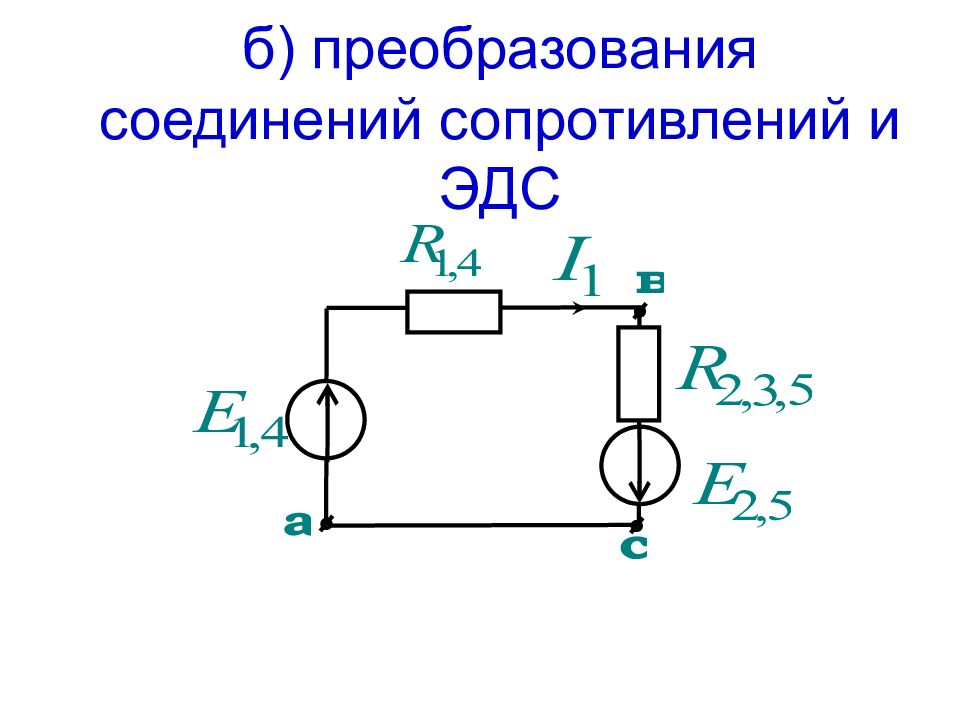
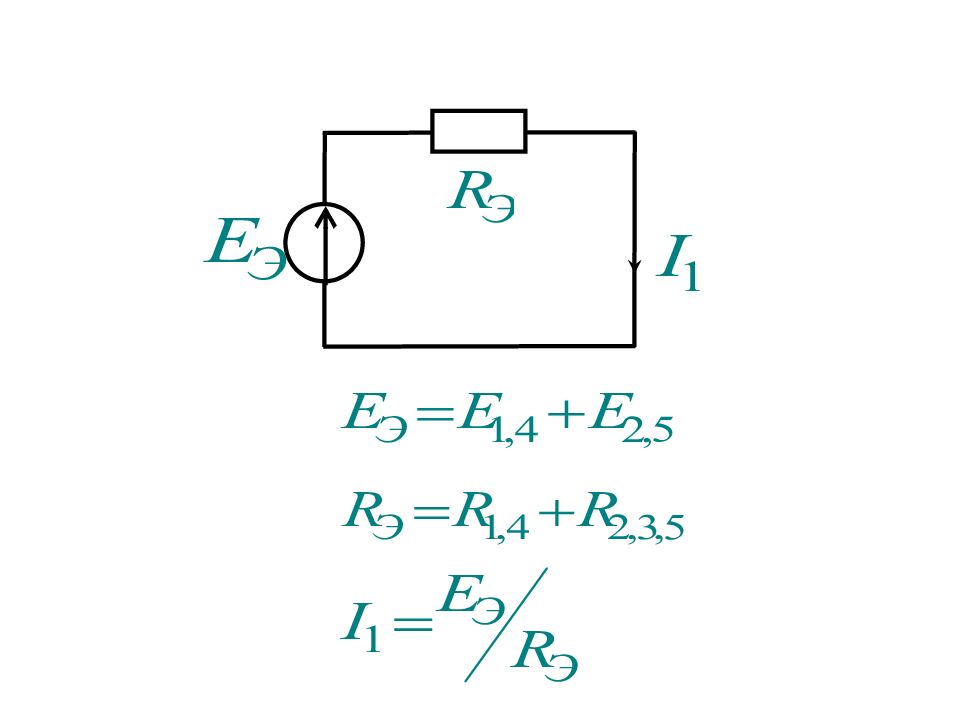
На основе приведенных правил можно реализовать метод преобразований для расчета тока или напряжения в любой ветви схемы. Для этого схема преобразуется до одного контура с искомым током или напряжением, где эти величины легко определяются
Слайд 27
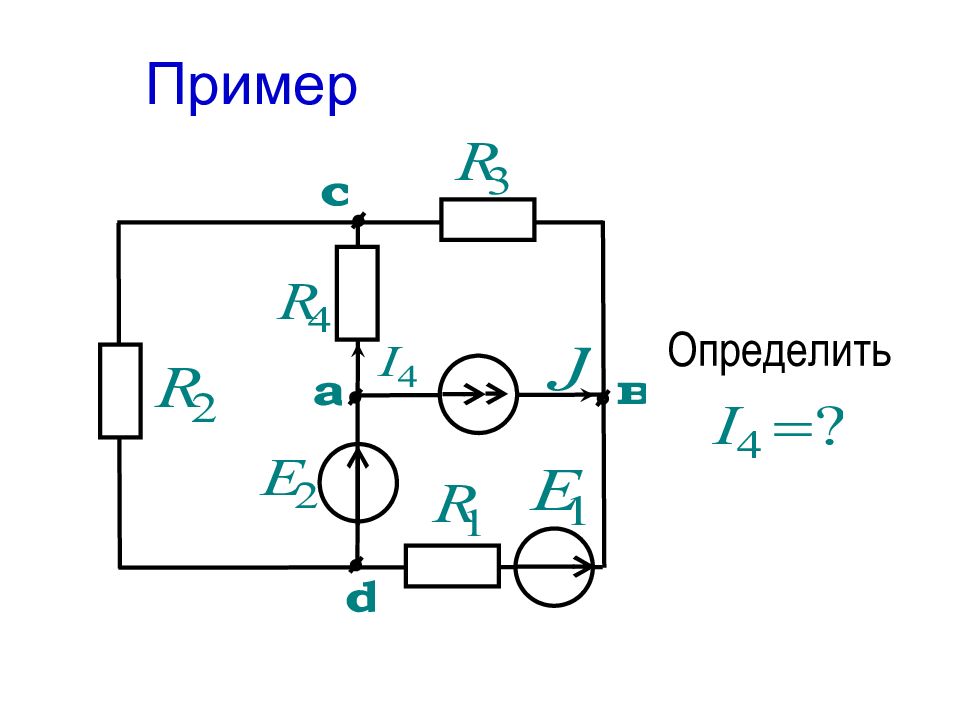
Метод наложения справедлив для линейных цепей и основывается на принципе наложения, когда любой ток (напряжение) равен алгебраической сумме составляющих от действия каждого источника в отдельности
Слайд 29
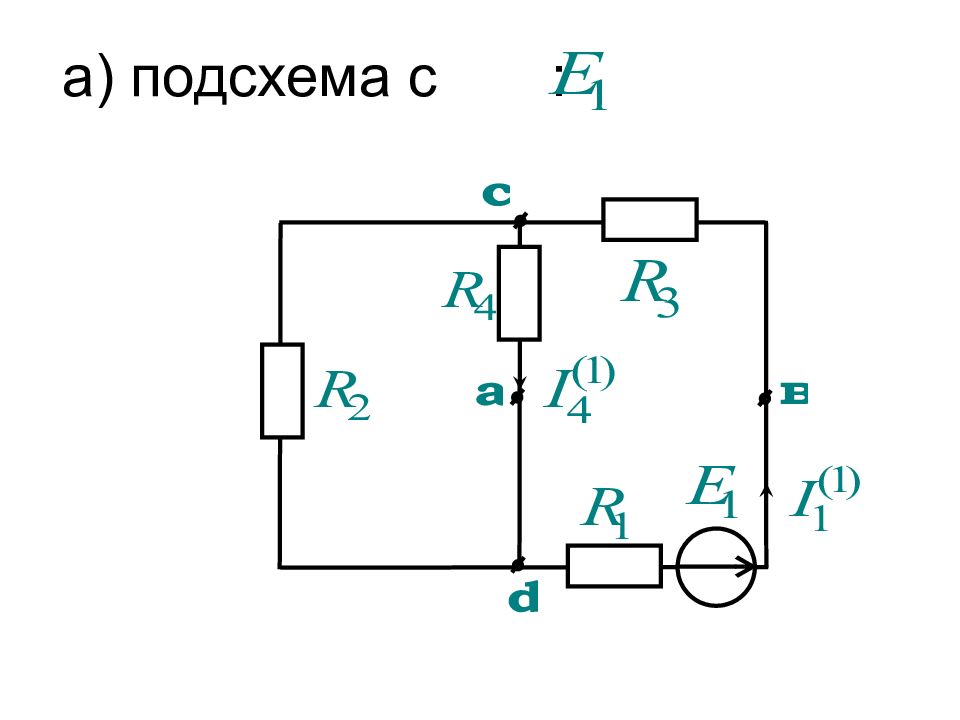
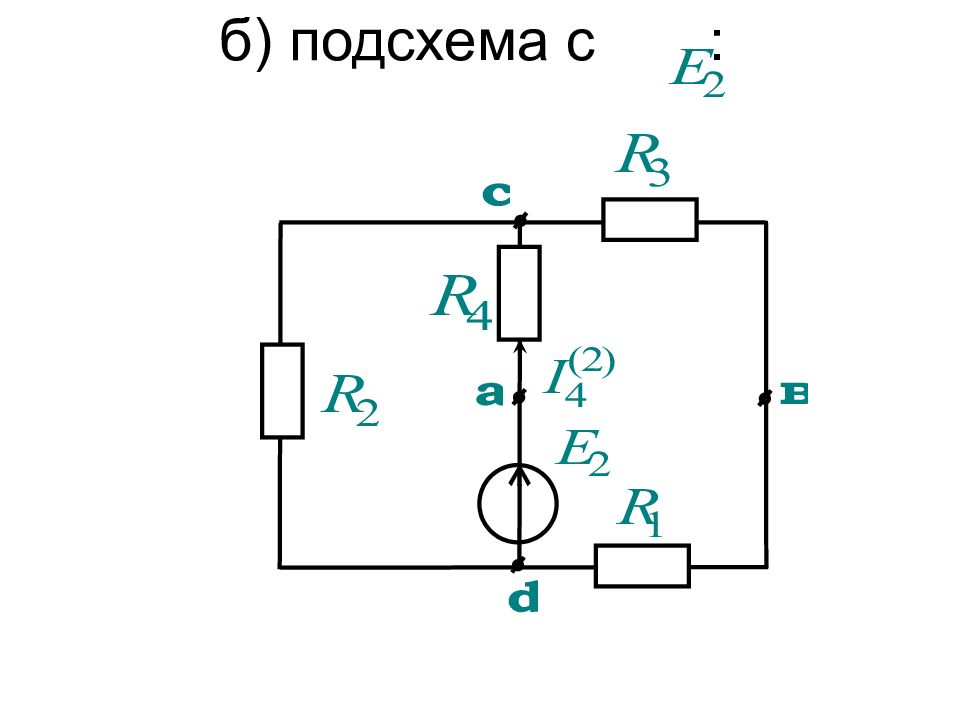
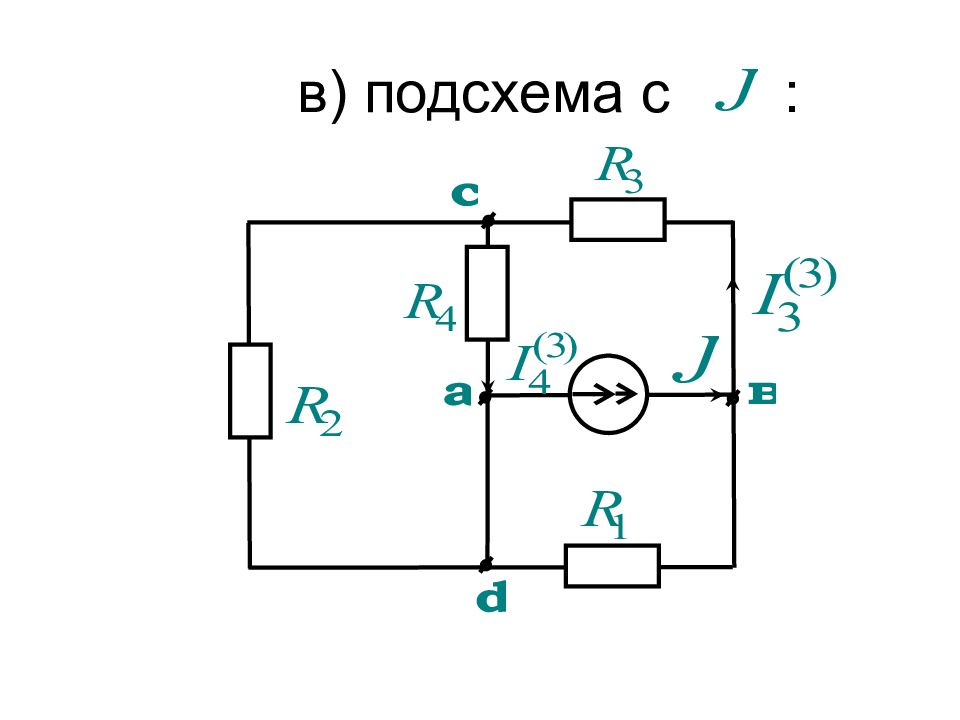
При этом для расчета составляющих токов и напряжений исходная схема разбивается на подсхемы, в каждой из которых действует один источник ЭДС или тока, причем остальные источники ЭДС закорочены, а ветви с остальными источниками тока разорваны
Слайд 39
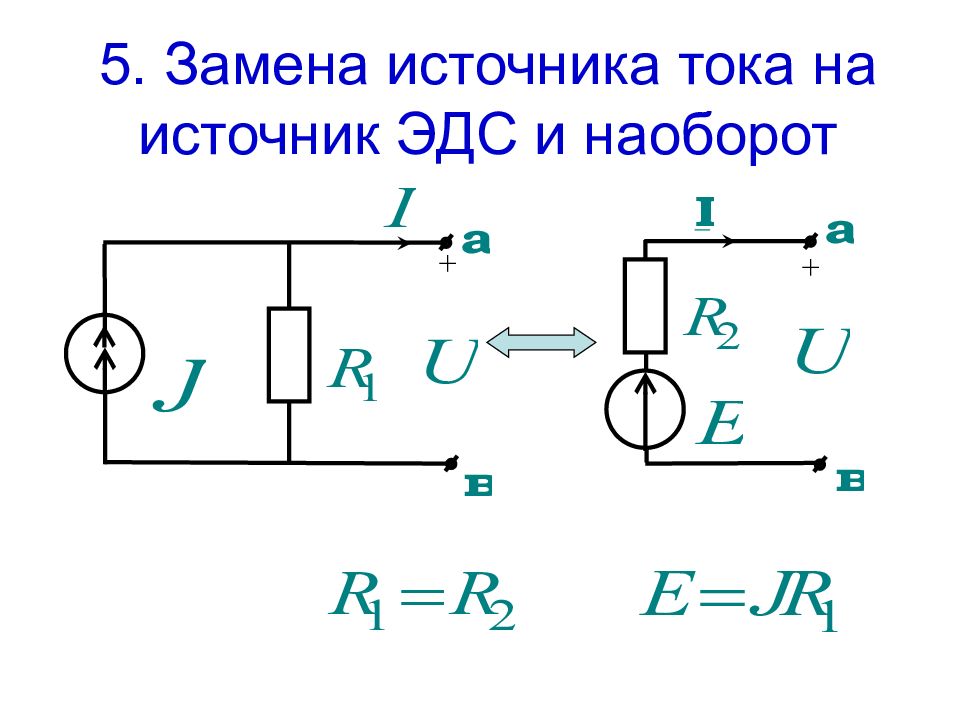
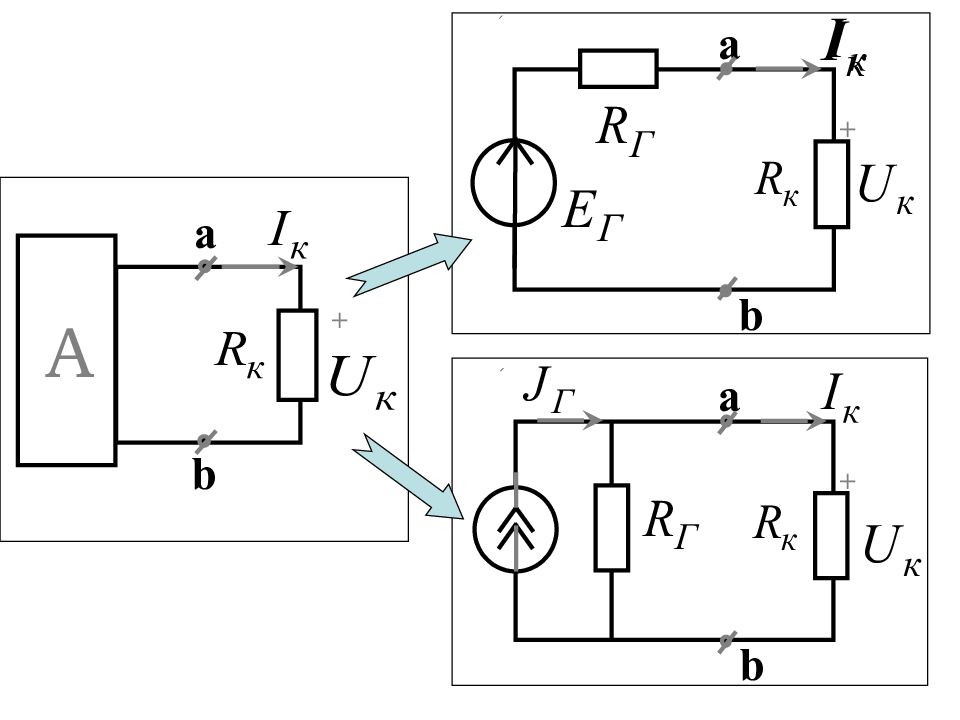
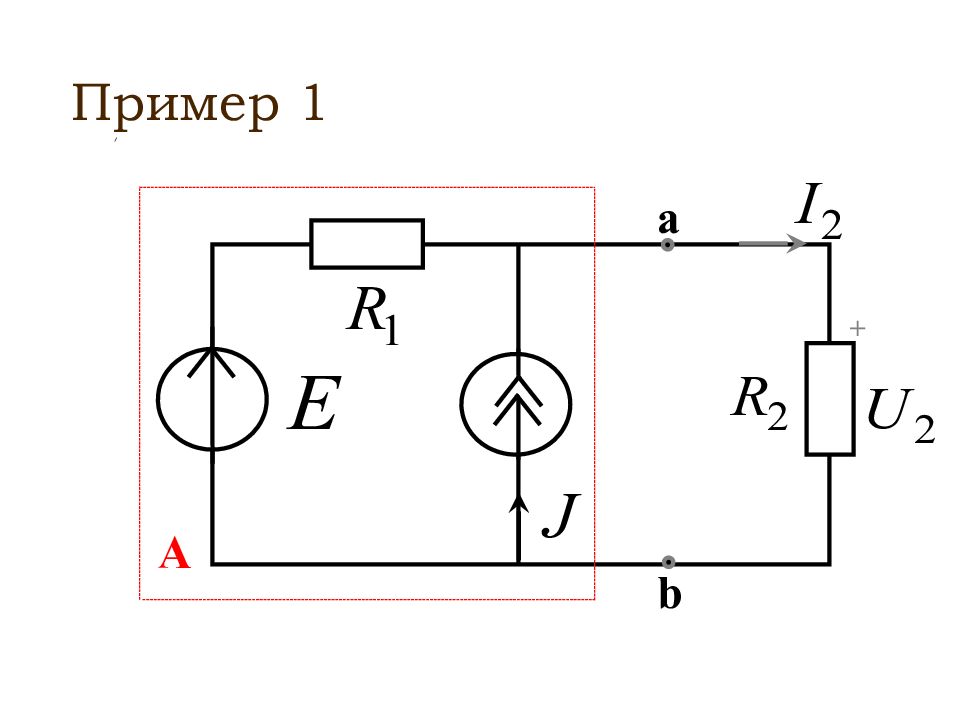
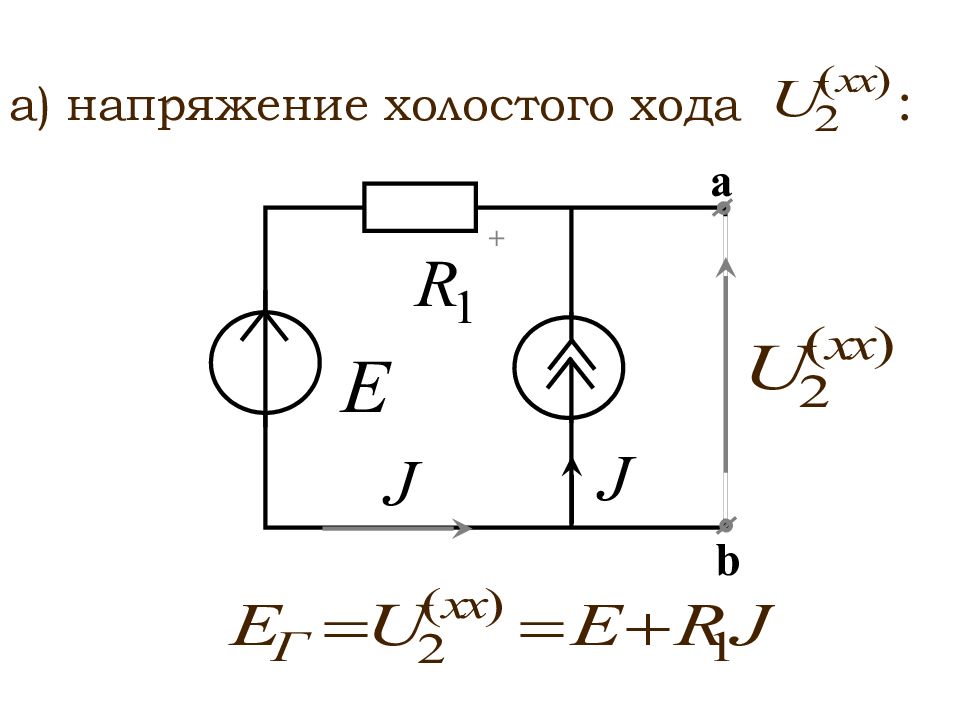
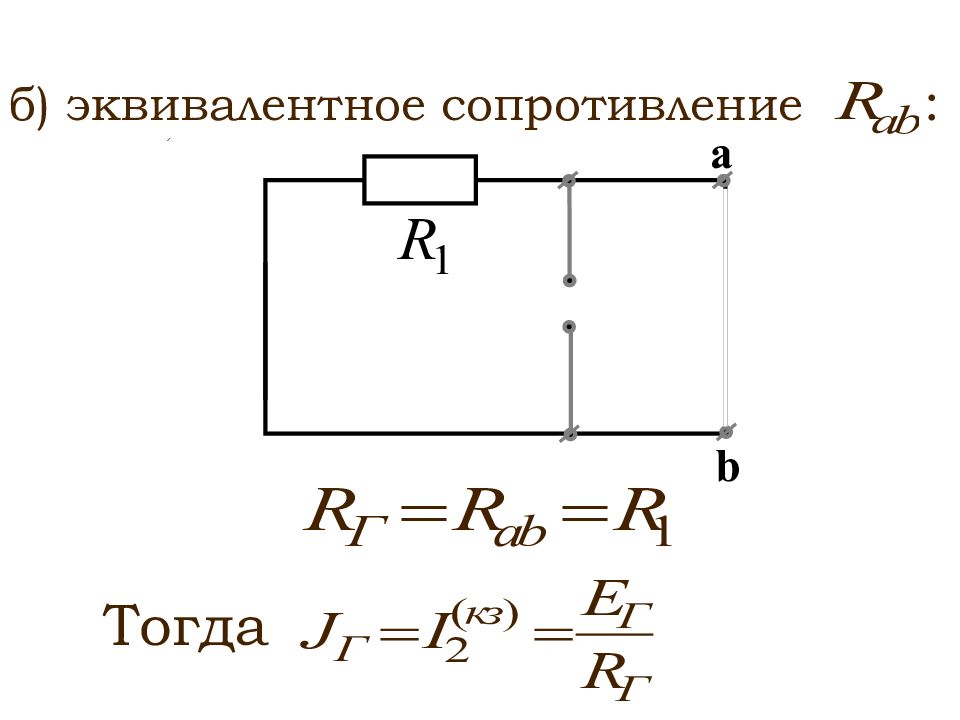
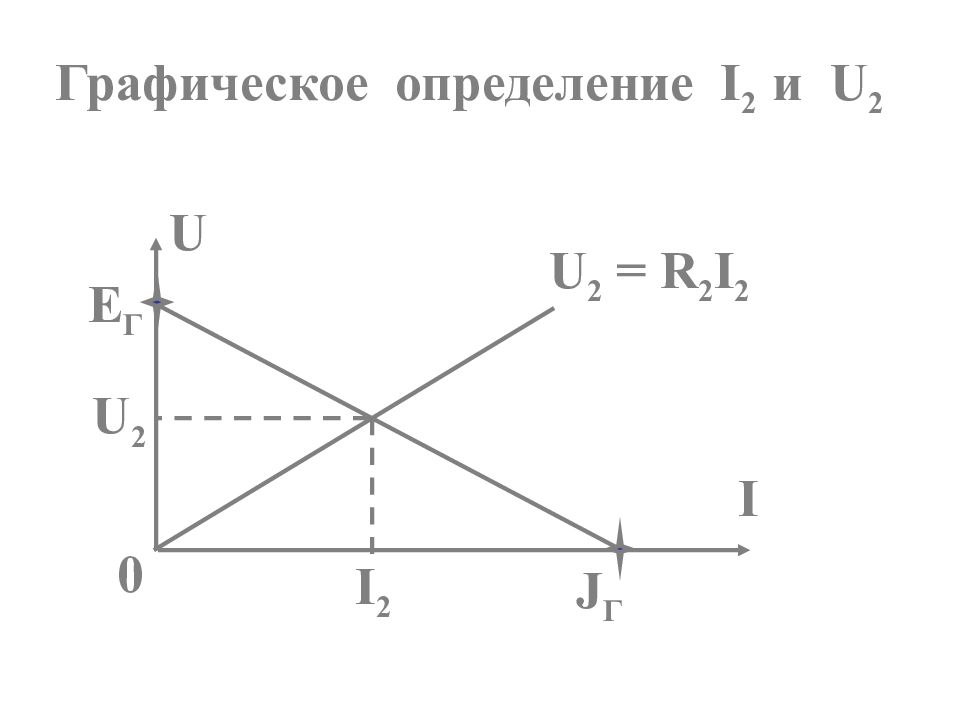
Любой активный двухполюсник, рассматриваемый относительно двух зажимов (выводов), можно представить в виде эквивалентного источника ЭДС или тока, с ЭДС и током равными соответственно напряжению холостого хода или току короткого замыкания относительно этих зажимов
Слайд 40
При этом внутреннее сопротивление этих источников равно эквивалентному сопротивлению активного двухполюсника относительно рассматриваемых зажимов
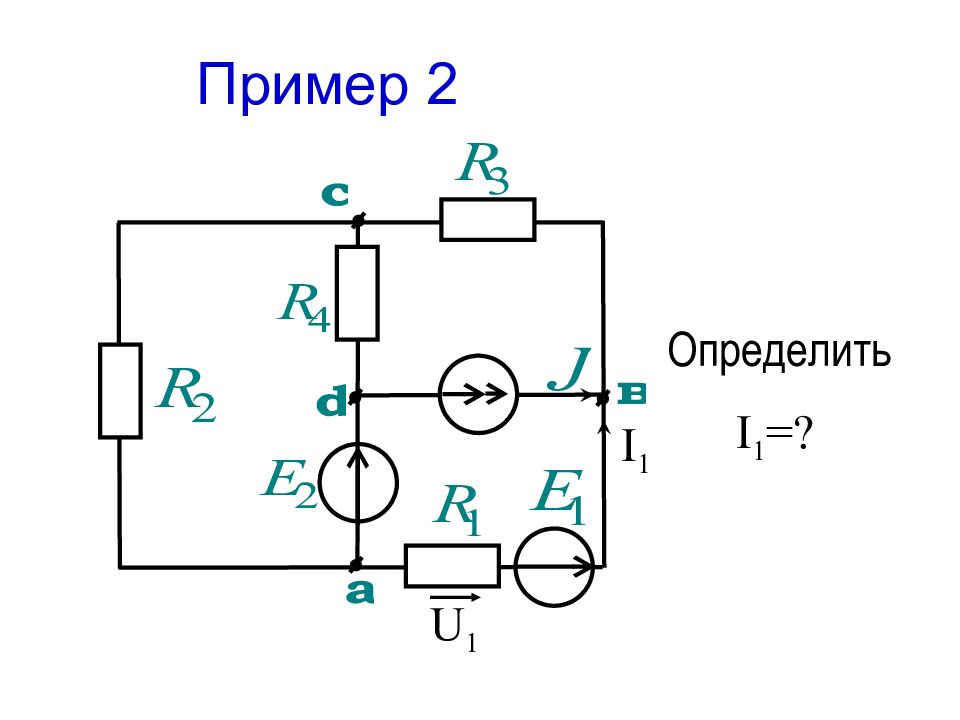
Слайд 52
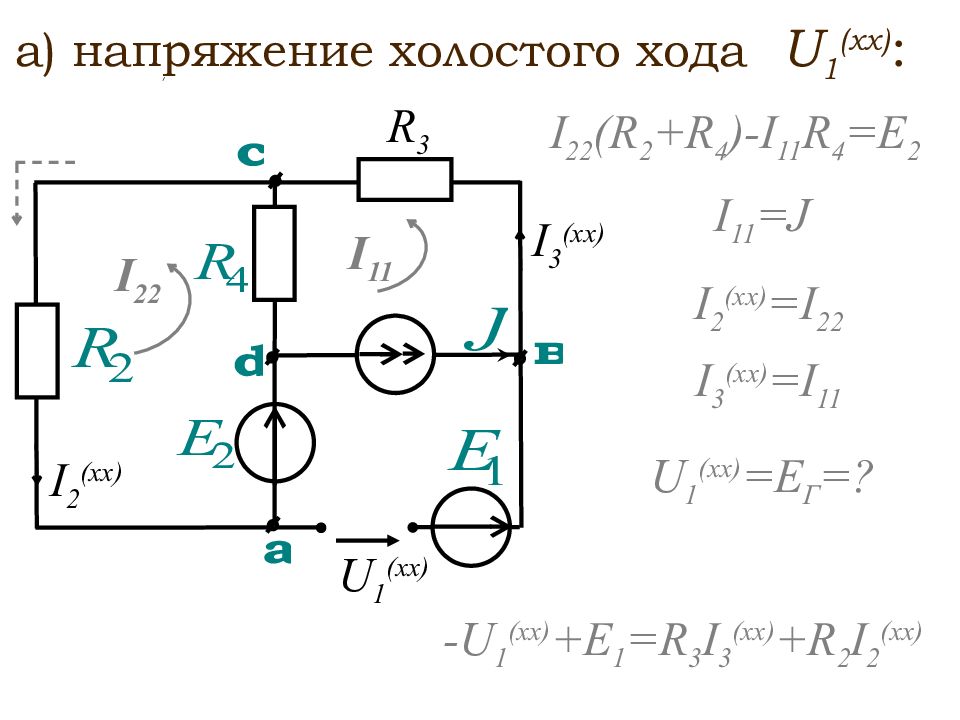
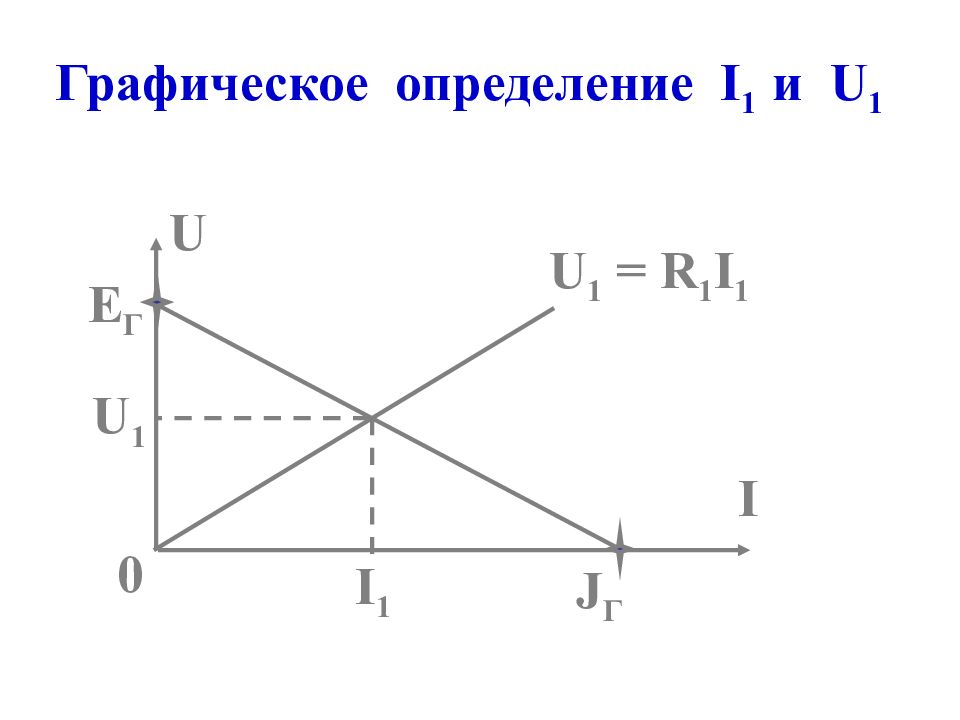
а) напряжение холостого хода U 1 (xx) : : R 3 U 1 (xx) I 11 I 22 I 3 (xx) I 2 (xx) I 11 =J I 22 (R 2 +R 4 )-I 11 R 4 =E 2 I 2 (xx) =I 22 I 3 (xx) =I 11 -U 1 (xx) +E 1 =R 3 I 3 (xx) +R 2 I 2 (xx) U 1 (xx) =E Г =?
Слайд 53
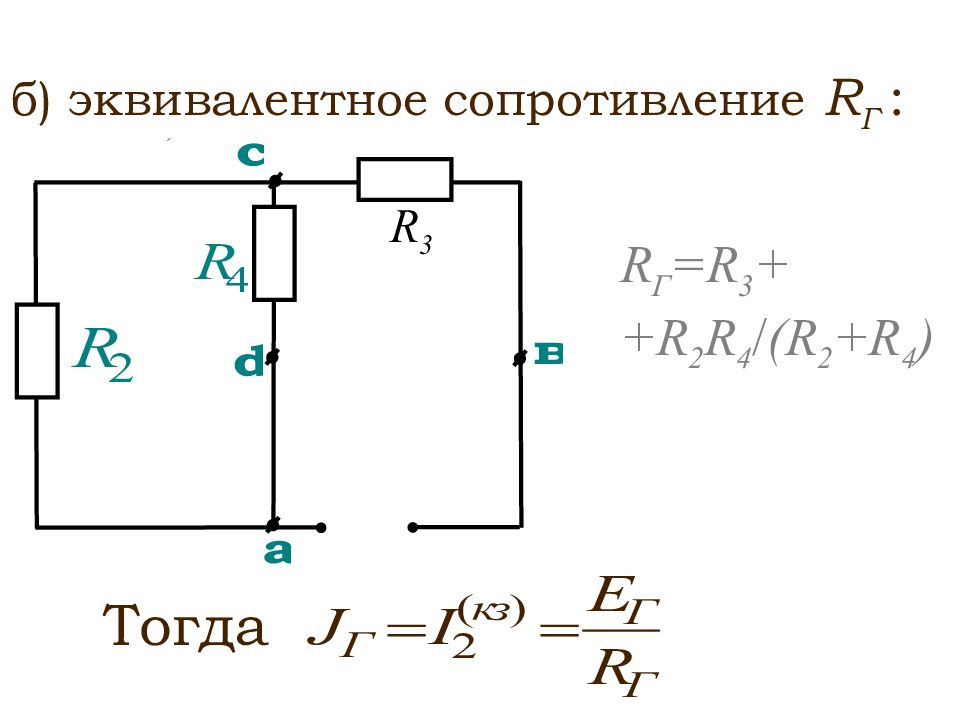
б) эквивалентное сопротивление R Г : : Тогда R 3 R Г =R 3 + + R 2 R 4 / (R 2 +R 4 )