Первый слайд презентации: Теоретические основы электротехники
Последовательность и методика выполнения задачи №1 по курсовой работе http://www.bestreferat.ru/referat-117052.html
Слайд 2: Теоретические основы электротехники
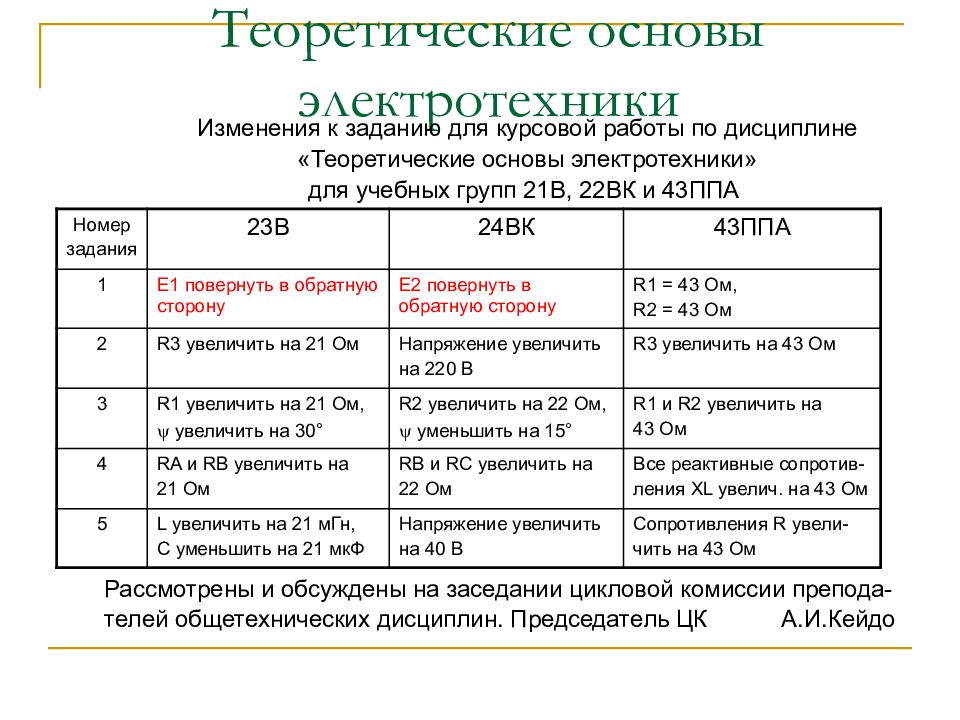
Изменения к заданию для курсовой работы по дисциплине «Теоретические основы электротехники» для учебных групп 21В, 22ВК и 43ППА Рассмотрены и обсуждены на заседании цикловой комиссии препода- телей общетехнических дисциплин. Председатель ЦК А.И.Кейдо Номер задания 23В 24ВК 43ППА 1 Е1 повернуть в обратную сторону Е2 повернуть в обратную сторону R1 = 43 Ом, R2 = 43 Ом 2 R3 увеличить на 21 Ом Напряжение увеличить на 220 В R3 увеличить на 43 Ом 3 R1 увеличить на 21 Ом, увеличить на 30 ° R2 увеличить на 22 Ом, уменьшить на 15 ° R1 и R2 увеличить на 43 Ом 4 RA и RB увеличить на 21 Ом RB и RC увеличить на 22 Ом Все реактивные сопротив- ления Х L увелич. на 43 Ом 5 L увеличить на 21 мГн, C уменьшить на 21 мкФ Напряжение увеличить на 40 В Сопротивления R увели- чить на 43 Ом
Слайд 3: Теоретические основы электротехники
Основные требования к текстовой документации
Слайд 5: Теоретические основы электротехники
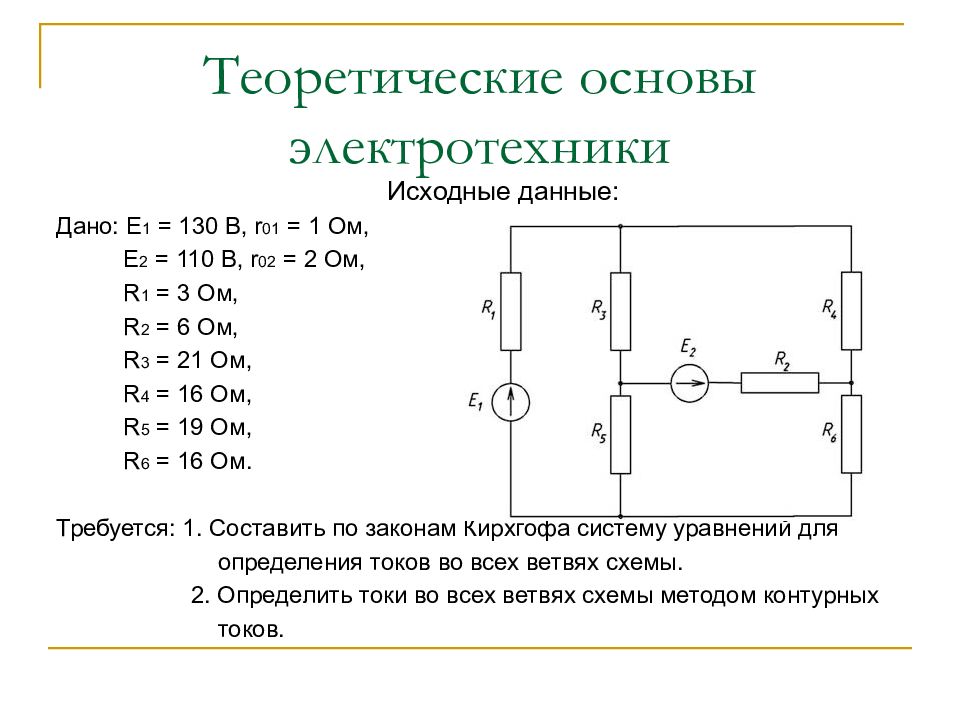
Исходные данные: Дано: Е 1 = 130 В, r 01 = 1 Ом, Е 2 = 110 В, r 02 = 2 Ом, R 1 = 3 Ом, R 2 = 6 Ом, R 3 = 21 Ом, R 4 = 16 Ом, R 5 = 19 Ом, R 6 = 16 Ом. Требуется: 1. Составить по законам Кирхгофа систему уравнений для определения токов во всех ветвях схемы. 2. Определить токи во всех ветвях схемы методом контурных токов.
Слайд 6: Теоретические основы электротехники
Требуется: 3. Составить баланс мощности для заданной схемы. 4. Определить токи во всех ветвях схемы на основании метода наложения. 5. Результаты расчетов токов по пунктам 2 и 4 представить в виде таблицы и сравнить. 6. Определить ток во второй ветви методом эквивалентного генератора. 7. Построить потенциальную диаграмму для любого контура, включающего обе ЭДС.
Слайд 7: Теоретические основы электротехники
Выполнение 1. Составление по законам Кирхгофа системы уравнений для определения токов во всех ветвях схемы Обозначаем токи ветвей и принимаем их направления на схеме, также обозначаем узлы схемы. В приведенной схеме 4 узла, значит по первому закону Кирхгофа нужно составить 3 уравнения: Узел 1: I 1 + I 4 – I 3 = 0. Узел 2: I 3 – I 2 – I 5 = 0. Узел 3: I 5 + I 6 – I 1 = 0. Всего в схеме 6 ветвей и 6 неизвес- тных токов – поэтому необходимо составить шесть уравнений.
Слайд 8: Теоретические основы электротехники
1. Составление по законам Кирхгофа системы уравнений для определения токов во всех ветвях схемы Недостающие 3 уравнения составляем по второму закону Кирхгофа. Для первого контура выберем обход по часовой стрелке: Е 1 = I 1 (R 1 + r 01 ) + I 5 R 5 + I 3 R 3. Для второго контура обход выберем против часовой стрелки: Е 2 = I 2 (R 2 + r 02 ) + I 4 R 4 + I 3 R 3. Для третьего контура направление обхода выберем по часовой стрелке: Е 2 = I 2 (R 2 + r 02 ) – I 5 R 5 +I 6 R 6.
Слайд 9: Теоретические основы электротехники
1. Составление по законам Кирхгофа системы уравнений для определения токов во всех ветвях схемы В результате получили систему из шести уравнений с шестью неизвестными токами: I 1 + I 4 – I 3 = 0 I 3 – I 2 – I 5 = 0 I 5 + I 6 – I 1 = 0 Е 1 = I 1 (R 1 + r 01 ) + I 5 R 5 + I 3 R 3 Е 2 = I 2 (R 2 + r 02 ) + I 4 R 4 + I 3 R 3 Е 2 = I 2 (R 2 + r 02 ) – I 5 R 5 +I 6 R 6 Решив полученную систему уравнений можно определить токи во всех ветвях схемы.
Слайд 10: Теоретические основы электротехники
2. Определить токи во всех ветвях схемы методом контурных токов На схеме выбираем направления контурных токов I 11, I 22, I 33, направ- ления обхода контуров оставляем такими же как и направления токов. Составляем уравнения для контурных токов по второму закону Кирхгофа: -Е 1 = I 11 (R 1 + r 01 + R 3 + R 5 ) -I 22 R 3 - I 33 R 5 E 2 = -I 11 R 3 + I 22 (R 2 + r 02 + R 3 + R 4 ) - I 33 (R 2 + r 02 ) -E 2 = -I 11 R 5 - I 22 (R 2 + r 02 ) + I 33 (R 2 + r 02 + R 5 + R 6 ) В полученную систему уравнений подставляем численные значения ЭДС и сопротивлений.
Слайд 11: Теоретические основы электротехники
2. Определить токи во всех ветвях схемы методом контурных токов -130 = I 11 • (3 +1+21+19) - I 22 • 21 - I 33 • 19 110 = -I 11 • 21 + I 22 • (6+2+21+16) - I 33 • (6+2) -110 = -I 11 • 19 - I 22 • (6+2) + I 33 • (6+2+19+16) Выполнив сложения в скобках получим следующую систему уравнений: - 130 = 44 I 11 – 21I 22 – 19I 33 110 = - 21I 11 + 45I 22 – 8I 33 -110 = -19I 11 – 8I 22 + 43I 33 Решим полученную систему уравнений с помощью определителей.
Слайд 12: Теоретические основы электротехники
2. Определить токи во всех ветвях схемы методом контурных токов Вычисляем главный определитель системы 44 -21 -19 = -21 45 -8 = 44 • 45 • 43 + (-21) • (-8) • (-19) + -19 -8 43 + (-19) • (-8) • (-21) – (-19) • 45 • (-19) – - (-8) • (-8) • 44 – 43 • (-21) • (-21) = 40732 Вычисляем частные определители: -130 -21 -19 11 = 110 45 -8 =(-130) • 45 • 43 + (-21)(-8)(-110)+ -110 -8 43 +(-19)(-8) • 110 – (-110) • 45 • (-19) – - (-8)(-8)(-130) – 43 • 110(-21) = -239710
Слайд 13: Теоретические основы электротехники
2. Определить токи во всех ветвях схемы методом контурных токов Вычисляем частные определители для контурных токов второго и третьего контуров: 44 -130 -19 22 = -21 110 -8 = 44 • 110 • 43 + (-130)(-8)(-19)+ -19 -110 43 + (-19)(-110)(-21) – (-19) • 110 • (-19) - – (-110)(-8) • 44 – 43 • (-21)(-130) = -51390 44 -21 -130 33 = -21 45 110 = 44 • 45 • (-110) + (-21)110(-19) + -19 -8 -110 + (-130)(-8)(-21) – (-19)45(-130) - - (-8)110 • 44 – (-110)(-21)(-21) = - 219670
Слайд 14: Теоретические основы электротехники
2. Определить токи во всех ветвях схемы методом контурных токов Определяем контурные токи: I 11 = 11 / = -239710 / 40732 = -5,885 A, I 22 = 22 / = -51390 / 40732 = -1,262 A, I 33 = 33 / = -219670 / 40732 = -5,393 A. Определяем токи ветвей I 1 = -I 11 = 5,885 A, I 2 = I 22 – I 33 = -1,262 - (-5,393) = 4,131 A, I 3 = I 22 – I 11 = -1,262 - (-5,885) = 4,623 A, I 4 = I 22 = -1,262 A, I 5 = I 33 – I 11 = -5,393 - (-5,885) = 0,493 A, I 6 = -I 33 = 5,393 A.
Слайд 15: Теоретические основы электротехники
3. Составление баланса мощности для заданной схемы C оставим баланс мощности Мощность источников: Р и = Е 1 • I 1 + E 2 • I 2 = 130 • 5,885 + 110 • 4,131 = = 1219,46 Вт. Мощность приемников: Р = I 1 ²(R 1 + r 01 ) + I 2 ²(R 2 + r 02 ) + I 3 ²R 3 + I 4 ² R 4 + I 5 ² R 5 + + I 6 ²R 6 = = 5,885² • (3 + 1) + 4,131² • (6 + 2) + 4,623² • 21 + (-1,262)² • 16 + + 0,493² • 19 + 5,393² • 16 = 1219,32 Вт. Таким образом, Ри = 1219,46 Вт Р = 1219,32 Вт – баланс мощности подтверждается – ошибка в расчетах составляет: (Ри – Р) / Ри = (1219,46 – 1219,32) / 1219,46 = 0,000115 • 100% = 0,0115%.
Слайд 16: Теоретические основы электротехники
4. Определить токи во всех ветвях схемы на основании метода наложения Определим частичные токи ветвей под действием источника Е 1. Для этого исключим из схемы источник Е 2, а вместо его оставим внутреннее сопротивление источника r 02. Нанесем на схеме частичные токи от ЭДС Е 1 и обозначим их с одним штрихом ( I ). Решаем задачу методом «свертывания», но для этого предва- рительно заменим звезду сопротивле- ний R 4 – R 6 – R 202 треугольником. Определим сопротивления сторон треугольника: R 4202 = R 4 + R 202 + R 4 • R 202 / R 6 = = 16 + (6+2) + 16 • (6+2) / 16 = 32 Ом, R 6202 = R 6 + R 202 + R 6 • R 202 / R 4 = = 16 + (6+2) + 16 • (6+2) / 16 = 32 Ом, r 02
Слайд 17: Теоретиче ские основы электротехники
4. Определить токи во всех ветвях схемы на основании метода наложения R46 = R4 + R6 + R4 • R6 / R202 = = 16 + 16 + 16 • 16 / (6+2) = 64 Ом. Определим эквивалентные сопротивле- ния параллельно соединенных резисторов: R 34202 = R 3 • R 4202 / (R 3 + R 4202 ) = = 21 • 32 / (21 + 32) = 12,679 Ом, R 56 202 = R 5 • R 6 202 / (R 5 + R 6 202 ) = = 19 • 32 / (19 + 32) = 11,922 Ом. Определим сопротивление последовательно соединенных резисторов R 3546202 = R 34202 + R 56202 = 12,679 + 11,922 = 24,601 Ом. Определим эквивалентное сопротивление относительно первой ветви R 1-3 = R 3546202 • R 46 / (R 3546202 + R 46 ) = 24,601 • 64 / (24,601 + 64) = 17,77Ом. E 1 R 1 I 1 I 3 I 5 R 3 R 5 R 4202 R 6202 R 46
Слайд 18: Теоретические основы электротехники
4. Определить токи во всех ветвях схемы на основании метода наложения Определим частичный ток в первое ветви I 1 = E 1 / (R 1-3 + R 1 + r 01 ) = 130 / ( 17,77 + 3 + 1) = 5,972 A. Определим ток в последовательном участке I 35-46 = I 1 • R 46 / (R 3546202 + R 46 ) = = 5,972 • 64 / (24,601 + 64) = 4,314 A. Определим частичные токи в третьем и пятом резисторах I 3 =I 35-46 •R 4202 /(R 3 +R 4202 )= 4,314 •32/(21+32)= 2,605 А, I 5 =I 35-46 •R 6 202 /(R 5 +R 6 202 )= 4,314 • 32/(19+32)=2,707 А. Для определения частичных токов в остальных ветвях схемы с источником Е 1 вернемся к исходной схеме с этим источником. E 1 R 1 I 1 I 3 I 5 R 3 R 5 R 4202 R 6202 R 46
Слайд 19: Теоретические основы электротехники
4. Определить токи во всех ветвях схемы на основании метода наложения Определим частичные токи во второй, четвертой и шестой ветвях на основании первого закона Кирхгофа: I 4 = I 1 – I 3 = 5,972 – 2,605 = 3,367 A, I 6 = I 1 – I 5 = 5,972 – 2,707 = 3,265 A, I 2 = I 3 – I 5 = 2,605 – 2,707 = -0, 102 A. Для определения частичных токов от действия источника Е 2 исключаем из схемы источник Е 1, вместо него включаем внутреннее сопротивление и частичные токи обозначаем с двумя штрихами. r 02
Слайд 20: Теоретические основы электротехники
4. Определить токи во всех ветвях схемы на основании метода наложения Частичные токи определяем методом «сворачивания» схемы, но предварительно треугольник сопротивлений ( R1+r01), R3, R5 заменяем эквивалентной звездой. Тогда схема будет иметь вид. Определим сопротивления лучей звезды: R 3101 = R 3 • R 101 / (R 3 + R 101 + R 5 ) = = 21 • (3+1) / (21 + 3 + 1 + 19) = 1,909 Ом, R 5 101 = R 5 • R 101 / (R 3 + R 101 + R 5 ) = = 19 • (3+1) / (21 + 3 + 1 + 19) = 1,727 Ом, R 35 = R 3 • R 5 / (R 3 + R 101 + R 5 ) = = 21 • 19 / (21 + 3 + 1 + 19) = 9,068 Ом. r 01 R 3101 R 35 R 5101 R 2 R 4 R 6 I 2 I 4 I 6 1 2 3 4
Слайд 21: Теоретические основы электротехники
4. Определить токи во всех ветвях схемы на основании метода наложения Определим эквивалентное сопротивление цепи относительно источника Е 2 : R э = (R 3101 + R 4 ) • (R 5101 + R 6 ) / (R 3101 + R 4 + R 5101 + R 6 ) + R 35 + R 2 = = (1,909 + 16) • (1,727 + 16) / (1,909 + 16 + 1,727 + 16) + 9,068 + 6 = 23,977 Ом. Определим ток в ветви с источником I 2 = E 2 / (R э + r 02 ) = 110 / (23,977 + 2) = 4,235 А. Определим токи в четвертой и шестой ветвях I 4 = I 2 • (R 5101 + R 6 ) / (R 3101 + R 4 + R 5101 + R 6 ) = = 4,235 • (1,727 + 16) / (1,909 + 16 + 1,727 + 16) = 2,107 A I 6 = I 2 • (R 3101 + R 4 ) / (R 3101 + R 4 + R 5101 + R 6 ) = = 4,235 • (1,909 + 16) / (1,909 + 16 + 1,727 + 16) = 2,128 A Для определения токов в первой, третьей и пятой ветвях возвращаемся к исходной схеме с источником Е 2. R 3101 R 35 R 5101 R 2 R 4 R 6 I 2 I 4 I 6 1 2 3 4
Слайд 22: Теоретические основы электротехники
4. Определить токи во всех ветвях схемы на основании метода наложения Определим потенциалы первого и третьего узлов, принимая потенциал четвертого узла равным нулю: 1 = - I 4 • R 4 = -2,107 • 16 = -33,712 B, 3 = - I 6 • R 6 = -2,128 • 16 = -34,048 B. Определим напряжение между третьим и первым узлами: U 31 = 3 - 1 = -34,048 – (-33,712) = -0,336 B. Определим частичный ток в первой ветви при действии источника Е 2 I 1 = U 31 / (R 1 + r 01 ) = -0,336 / (3 + 1) = -0,084 A. Для определения токов в третьей и пятой ветвях воспользуемся первым законом Кирхгофа: I 3 = I 1 + I 4 = -0,084 + 2,107 = 2,023 A, I 5 = I 6 - I 1 = 2,128 – (-0,084) = 2,212 A. r 01
Слайд 23: Теоретические основы электротехники
4. Определить токи во всех ветвях схемы на основании метода наложения Определяем токи ветвей: I 1 = I 1 + I 1 = 5,972 – 0,084 = 5,888 А, I 2 = I 2 + I 2 = -0,102 + 4,235 = 4,133 А, I 3 = I 3 + I 3 = 2,605 + 2,023 = 4,628 А, I 4 = I 4 - I 4 = 2,107 – 3,367 = -1,26 А, I 5 = I 5 - I 5 = 2,707 – 2,212 = 0,495 А, I 6 = I 6 + I 6 = 3,265 +2,128 = 5,393 А. r 02 r 01
Слайд 24: Теоретические основы электротехники
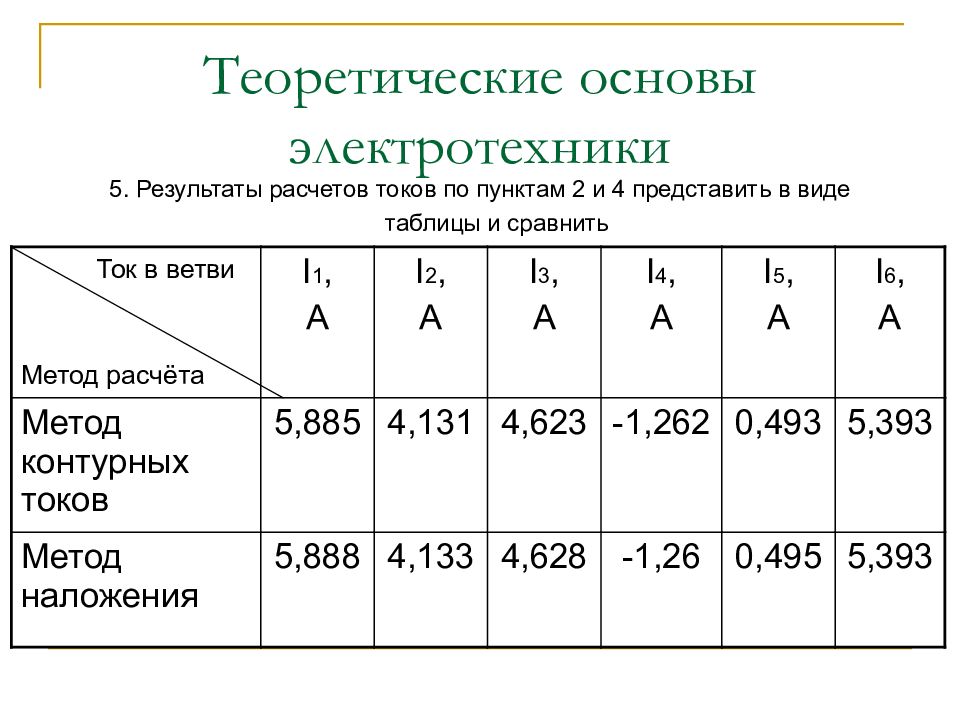
5. Результаты расчетов токов по пунктам 2 и 4 представить в виде таблицы и сравнить I 1, A I 2, A I 3, A I 4, A I 5, A I 6, A Метод контурных токов 5,885 4,131 4,623 -1,262 0,493 5,393 Метод наложения 5,888 4,133 4,628 -1,26 0,495 5,393 Метод расчёта Ток в ветви
Слайд 25: Теоретические основы электротехники
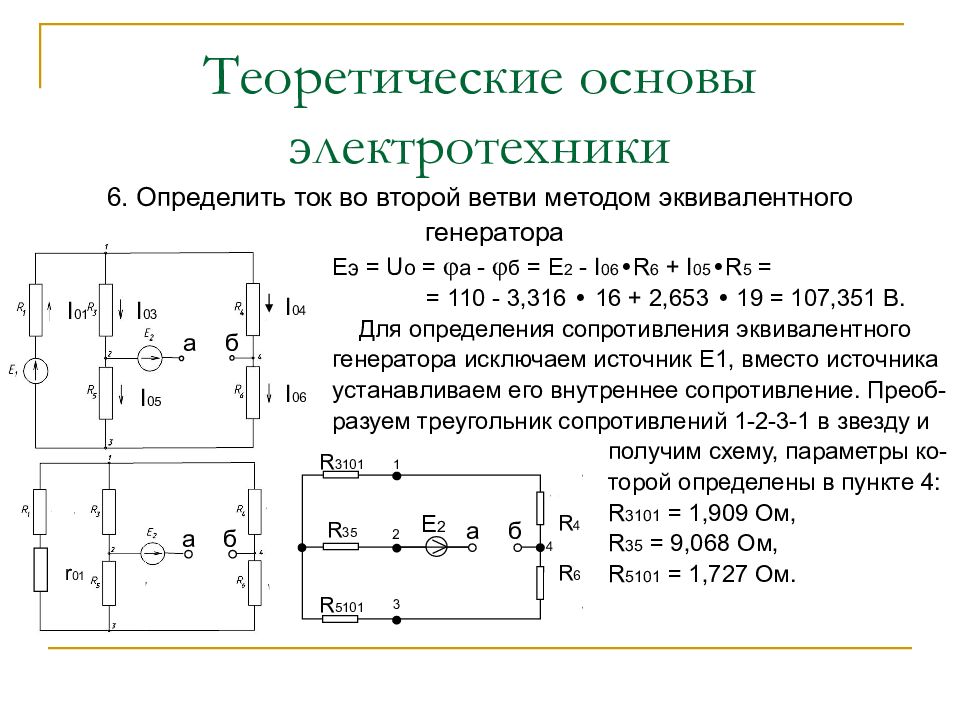
6. Определить ток во второй ветви методом эквивалентного генератора Для определения эквивалентной ЭДС Е э или напряже- ния холостого хода U о исключаем во второй ветви резис- тор R 2, оставляем ветвь разомкнутой с зажимами а и б и определяем напряжение между этими зажимами, которое и называется напряжением холостого хода. Для определения U о рассчитаем токи I 01, I 05 и I 06 R 3546 = (R 3 + R 5 ) • (R 4 + R 6 ) / (R 3 + R 5 + R 4 + R 6 ) = = (21 + 19) • (16 + 16) / (21 + 19 + 16 + 16) = 17,778 Ом, I 01 = Е 1 / ( R 3546 + R 1 +r 01 ) =130/(17,778+3+1)=5,969 A I 05 = I 01 • (R 4 + R 6 ) / (R 3 + R 5 + R 4 + R 6 ) = = 5,969 • (16 + 16) / (21 + 19 + 16 + 16) = 2,653 A, I 06 = I 01 • (R 3 + R 5 ) / (R 3 + R 5 + R 4 + R 6 ) = = 5,969 • (21 + 19) / (21 + 19 + 16 + 16) = 3,316 A. I 01 I 03 I 05 I 04 I 06 a б
Слайд 26: Теоретические основы электротехники
6. Определить ток во второй ветви методом эквивалентного генератора E э = U o = a - б = Е 2 - I 06 • R 6 + I 05 • R 5 = = 110 - 3,316 • 16 + 2,653 • 19 = 1 07,351 B. Для определения сопротивления эквивалентного генератора исключаем источник Е1, вместо источника устанавливаем его внутреннее сопротивление. Преоб- разуем треугольник сопротивлений 1-2-3-1 в звезду и получим схему, параметры ко- торой определены в пункте 4: R 3101 = 1,909 Ом, R 35 = 9,068 Ом, R 5101 = 1,727 Ом. I 01 I 03 I 05 I 04 I 06 a б R 3101 R 35 R 5101 R 2 R 4 R 6 I 2 I 4 I 6 1 2 3 4 а б r 01 а б E 2
Слайд 27: Теоретические основы электротехники
6. Определить ток во второй ветви методом эквивалентного генератора Тогда сопротивление эквивалентного генератора составит: r э = (R 3101 + R 4 ) • (R 5101 + R 6 )/(R 3101 + R 4 + R 5101 + R 6 ) + R 35 + + r 02 = (1,909+16) • (1,727+16)/(1,909+16+1,727+16) + + 9,068 + 2 = 19, 977 Ом. Определяем ток во второй ветви схемы: I 2 = E э / (r э + R 2 ) = 107,351 / (19,977 + 6) = 4,133 А. Таким образом, при расчете методом эквивалентного генератора ток во второй ветви получился таким же, как и при расчете методом контурных токов и методом наложения. R 3101 R 35 R 5101 R 2 R 4 R 6 I 2 I 4 I 6 1 2 3 4 а б E 2
Слайд 28: Теоретические основы электротехники
7. Построить потенциальную диаграмму для любого контура, включающего обе ЭДС Для построения потенциальной диаграммы выбираем контур с двумя источниками питания. Такому условию соответствует контур, отмеченный на ниж- нем рисунке. Выбираем в качестве начального узел 1 и придаем ему потенциал, равный нулю. Для расчета потенциалов осталь- ных точек обходим контур по часовой стрелке. Тогда: 1 = 0, 4 = 1 + I 4 • R 4 = 0 + (-1,262 • 16) = -20,2 B, 5 = 4 + I 2 • R 2 = -20,2 + 4,131 • 6 = 4,6 B, 2 = 5 - E 2 + I 2 • r 02 = 4,6 - 110 + 4,131 • 2 = -97,1 B, 3 = 2 – I 5 • R 5 = -97,1 – 0,493 • 19 = -106,5 B, 6 = 3 + E 1 – I 1 • r 01 = -106,5 + 130 – 5,885 • 1 = 17,6 B, 1 = 6 – I 1 • R 1 = 17,6 – 5,885 • 3 = -0,06 B – проверочная точка. 5 6
Слайд 29: Теоретические основы электротехники
7. Построить потенциальную диаграмму для любого контура, включающего обе ЭДС По полученным данным строим для контура потенциальную диаграмму - зависимость потенциалов точек от сопротивлений участков контура.
Слайд 30: Теоретические основы электротехники
Резисторы Стандартный ряд номинальных мощностей резисторов 0,01; 0,025; 0,05; 0,125; 0,25; 0,5; 1,0; 2,0 Вт Обозначение резисторов
Слайд 31: Теоретические основы электротехники
Последовательность и методика выполнения задачи №2 по курсовой работе
Слайд 32: Теоретические основы электротехники
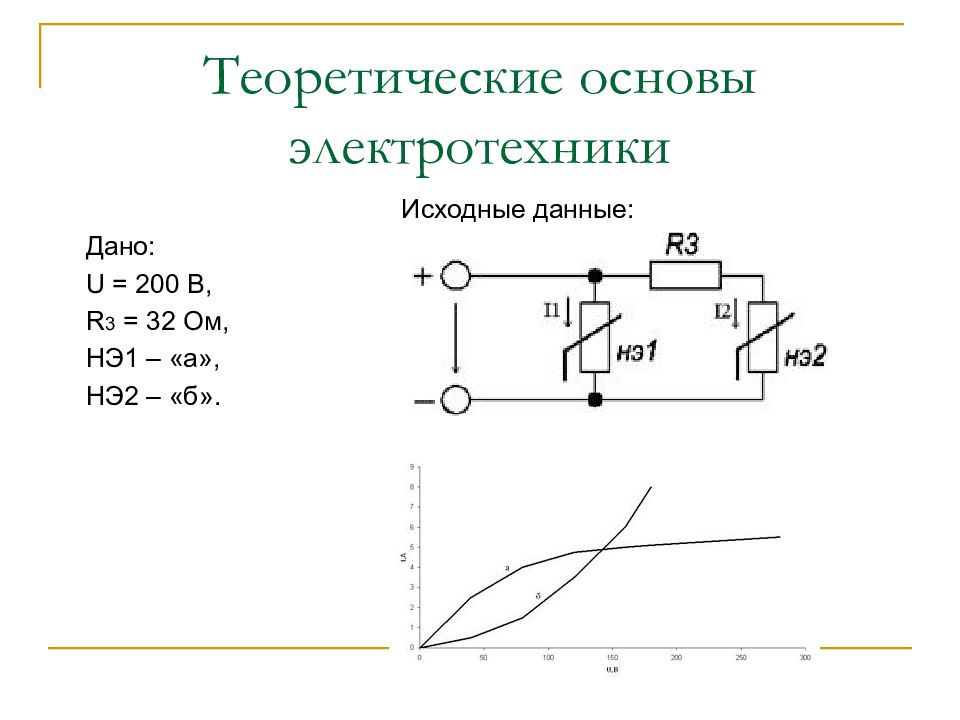
Исходные данные: Дано: U = 200 B, R 3 = 32 Ом, НЭ1 – «а», НЭ2 – «б».
Слайд 33: Теоретические основы электротехники
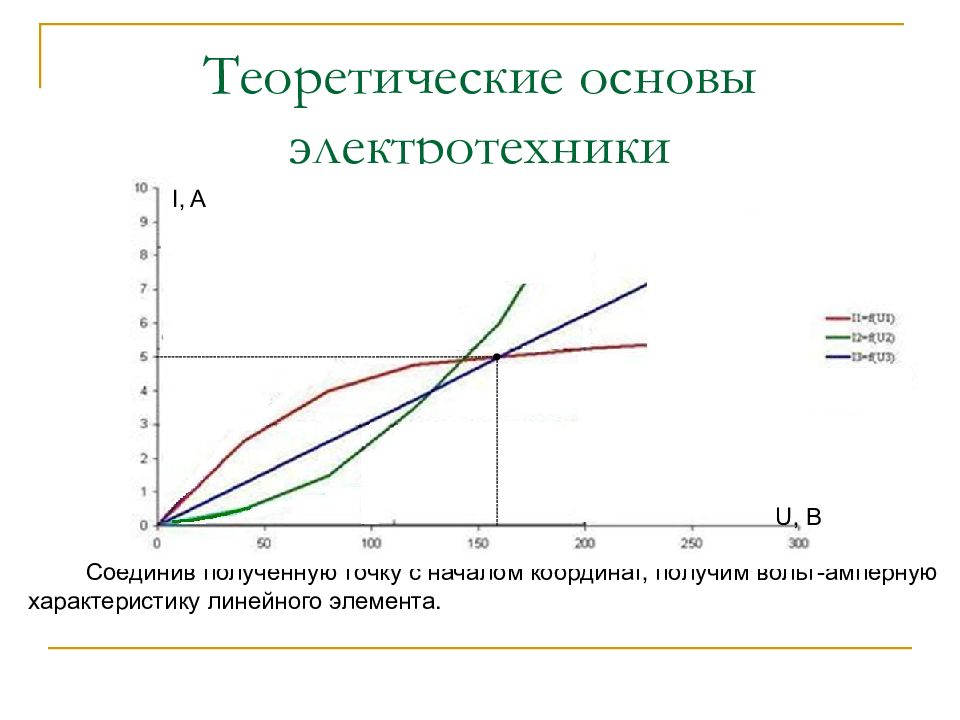
Требуется: 1. Определить графическим методом все токи. 2. Определить напряжения на всех участках цепи. Р е ш е н и е 1. Расчет цепи производим графическим методом. Для этого в общей системе координат ( U,I ) строим заданные вольт-амперные характеристики нелинейных элементов (НЭ1 и НЭ2). Для построения характеристик принимаем масштабы: Для напряжений M u = 25 B/c м. Для токов M I = 1 A/c м. Для построения вольт-амперной характеристики линейного элемента ( R 3 ) определим координаты одной из точек характеристики. Пусть абсциссой этой точки будет U = 160 B. Тогда ордината этой точки составит: I = U / R3 = 160 / 32 = 5 A.
Слайд 34: Теоретические основы электротехники
Р е ш е н и е Соединив полученную точку с началом координат, получим вольт-амперную характеристику линейного элемента. I, A U, B
Слайд 35: Теоретические основы электротехники
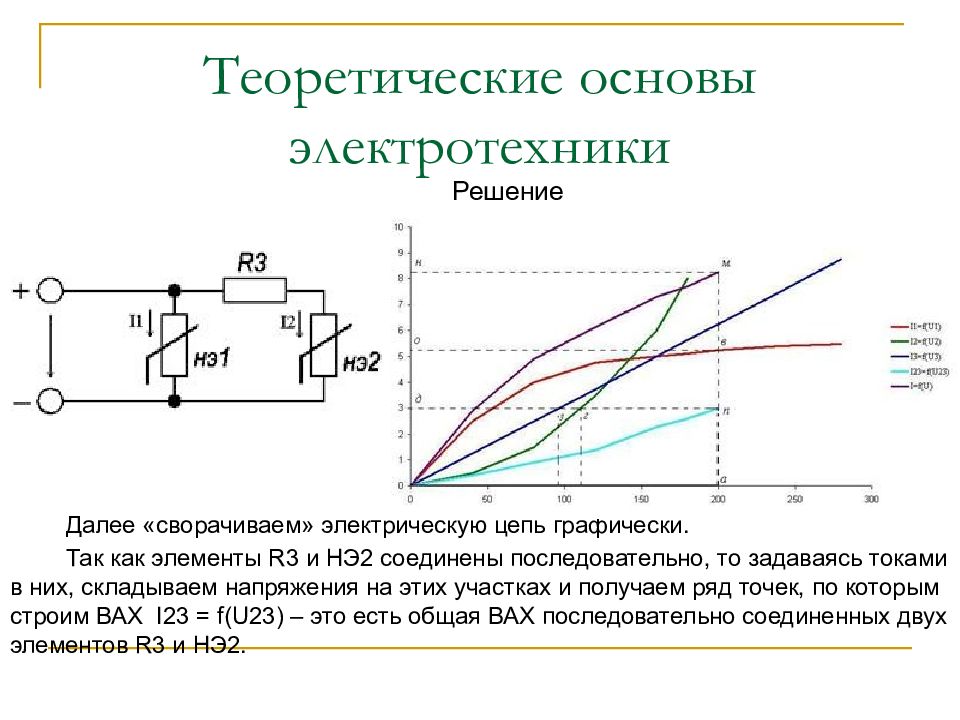
Решение Далее «сворачиваем» электрическую цепь графически. Так как элементы R3 и НЭ2 соединены последовательно, то задаваясь токами в них, складываем напряжения на этих участках и получаем ряд точек, по которым строим ВАХ I23 = f(U23) – это есть общая ВАХ последовательно соединенных двух элементов R3 и НЭ2.
Слайд 36: Теоретические основы электротехники
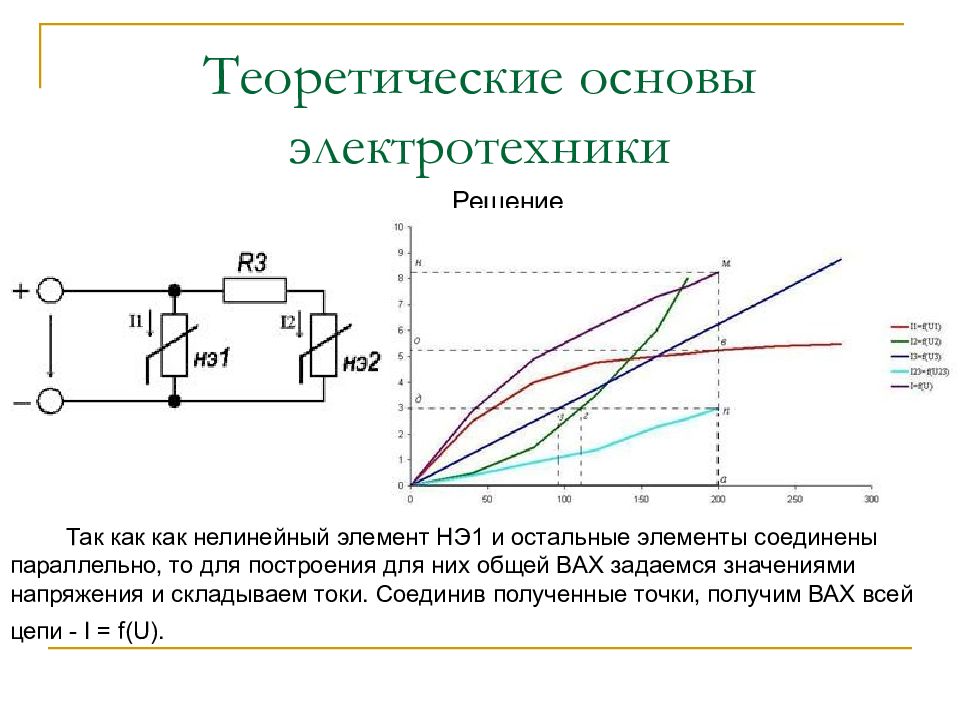
Решение Так как как нелинейный элемент НЭ1 и остальные элементы соединены параллельно, то для построения для них общей ВАХ задаемся значениями напряжения и складываем токи. Соединив полученные точки, получим ВАХ всей цепи - I = f(U).
Слайд 37: Теоретические основы электротехники
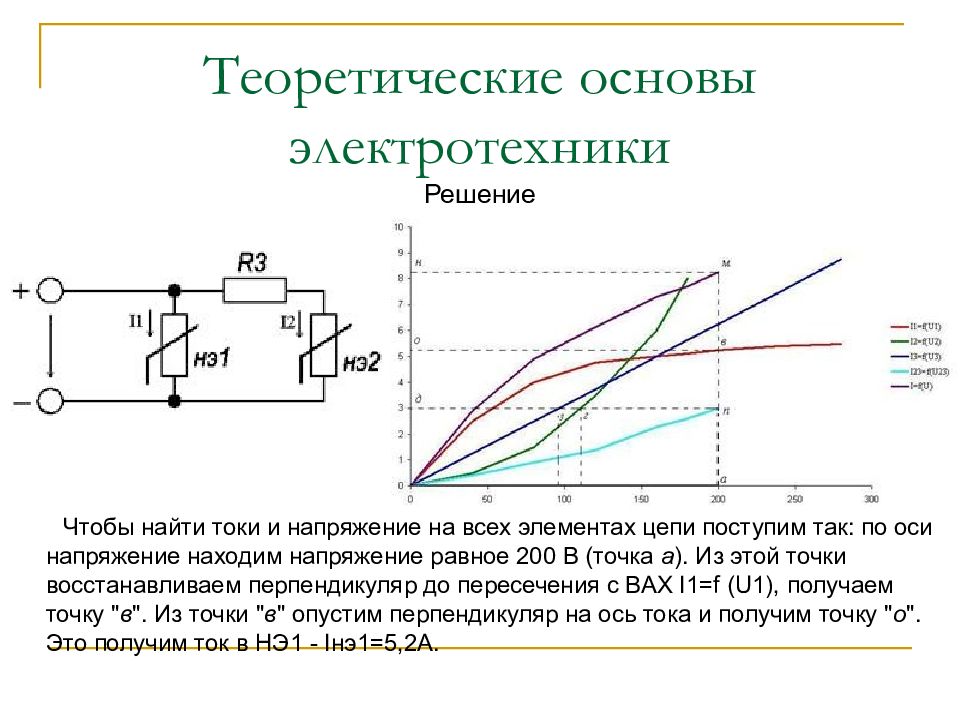
Решение Чтобы найти токи и напряжение на всех элементах цепи поступим так: по оси напряжение находим напряжение равное 200 В (точка а ). Из этой точки восстанавливаем перпендикуляр до пересечения с ВАХ I1=f (U1), получаем точку " в ". Из точки " в " опустим перпендикуляр на ось тока и получим точку " о ". Это получим ток в НЭ1 - Iнэ1=5,2А.
Слайд 38: Теоретические основы электротехники
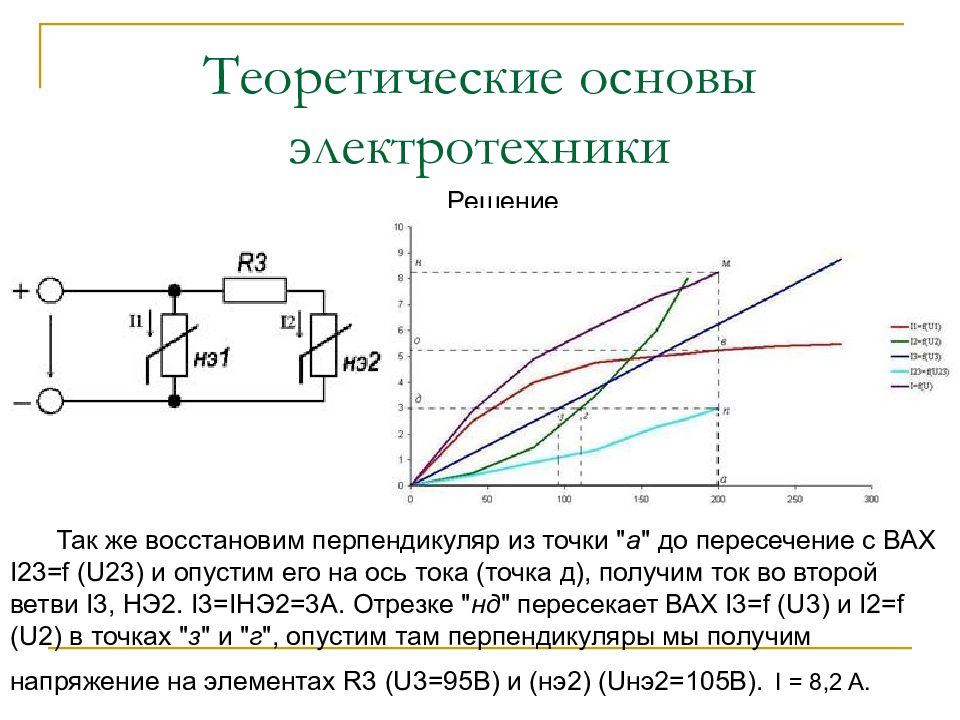
Решение Так же восстановим перпендикуляр из точки " а " до пересечение с ВАХ I23=f (U23) и опустим его на ось тока (точка д), получим ток во второй ветви I3, НЭ2. I3=IНЭ2=3А. Отрезке " нд " пересекает ВАХ I3=f (U3) и I2=f (U2) в точках " з " и " г ", опустим там перпендикуляры мы получим напряжение на элементах R3 (U3=95В) и (нэ2) (Uнэ2=105В). I = 8,2 A.
Слайд 41: Теоретические основы электротехники
Последовательность и методика выполнения задачи №3 по курсовой работе
Слайд 42: Теоретические основы электротехники
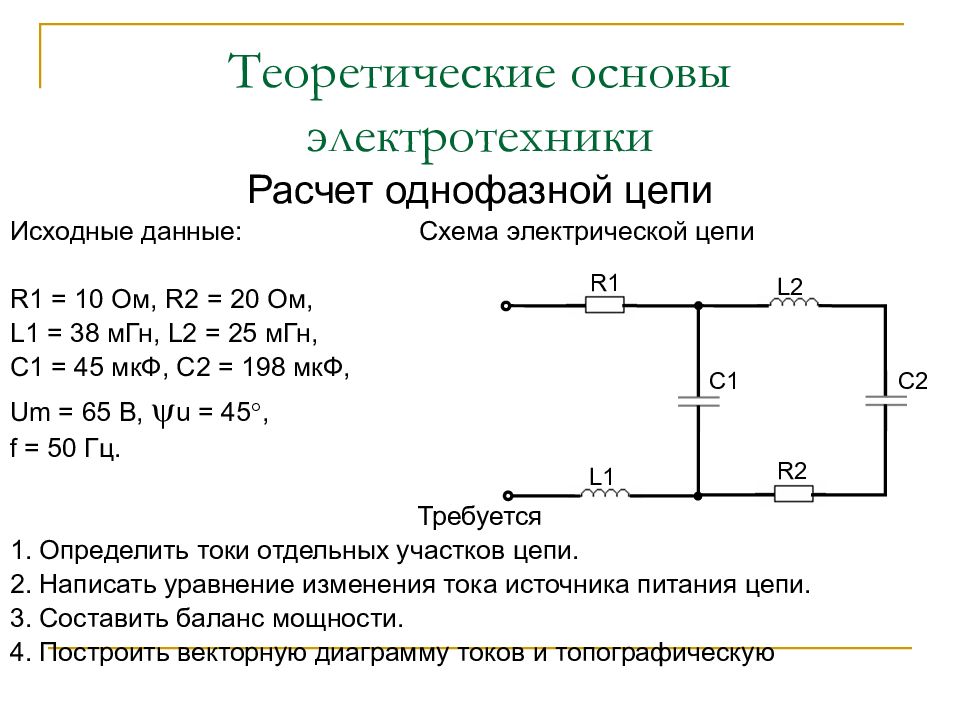
Расчет однофазной цепи Исходные данные: Схема электрической цепи R1 = 10 Ом, R2 = 20 Ом, L1 = 38 мГн, L2 = 25 мГн, C1 = 45 мкФ, C2 = 198 мкФ, Um = 65 B, u = 45, f = 50 Гц. Требуется 1. Определить токи отдельных участков цепи. 2. Написать уравнение изменения тока источника питания цепи. 3. Составить баланс мощности. 4. Построить векторную диаграмму токов и топографическую R1 R2 L1 L2 C1 C2
Слайд 44: Теоретические основы электротехники
Последовательность и методика выполнения задачи №4 по курсовой работе
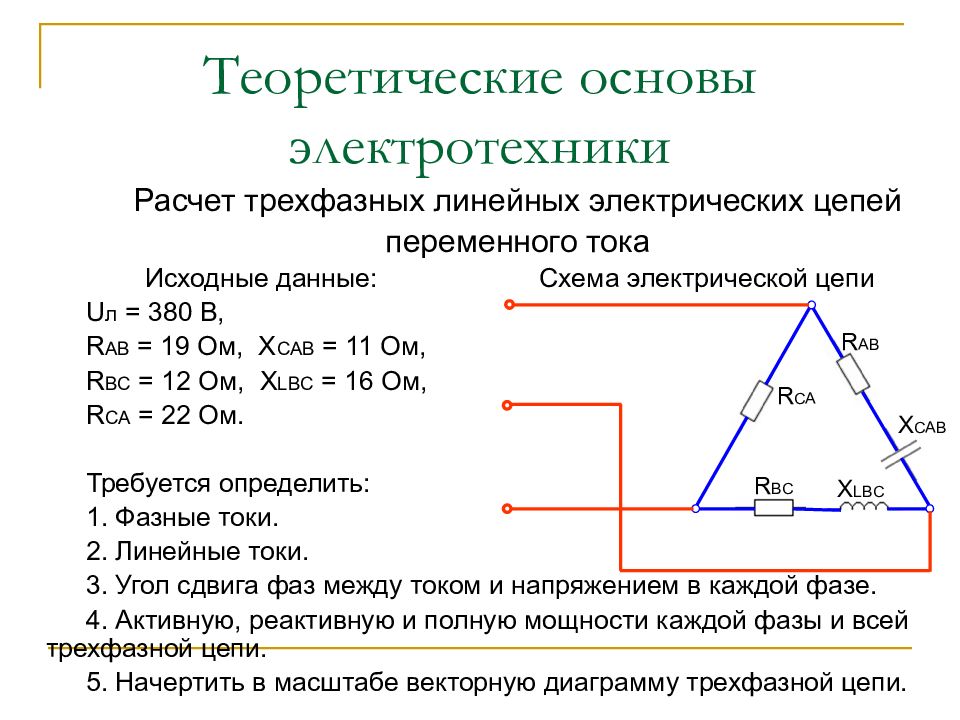
Слайд 45: Теоретические основы электротехники
Расчет трехфазных линейных электрических цепей переменного тока Исходные данные: Схема электрической цепи U л = 380 B, R AB = 19 Ом, X CAB = 11 Ом, R BC = 12 Ом, X LBC = 16 Ом, R CA = 22 Ом. Требуется определить: 1. Фазные токи. 2. Линейные токи. 3. Угол сдвига фаз между током и напряжением в каждой фазе. 4. Активную, реактивную и полную мощности каждой фазы и всей трехфазной цепи. 5. Начертить в масштабе векторную диаграмму трехфазной цепи. R AB X CAB R BC X LBC R CA
Слайд 46: Теоретические основы электротехники
Расчет трехфазных линейных электрических цепей переменного тока Решение Для расчета трехфазной цепи применим символический метод. 1. При соединении нагрузки треугольником модули фазных напряжений равны линейным напряжениям: U ф = U л = 380 B, то есть U AB = U BC = U CA = 380 B. 2. Комплексы данных напряжений запишем из условия, что вектор фазного напряжения U АВ совпадает с действительной осью комплексной плоскости:
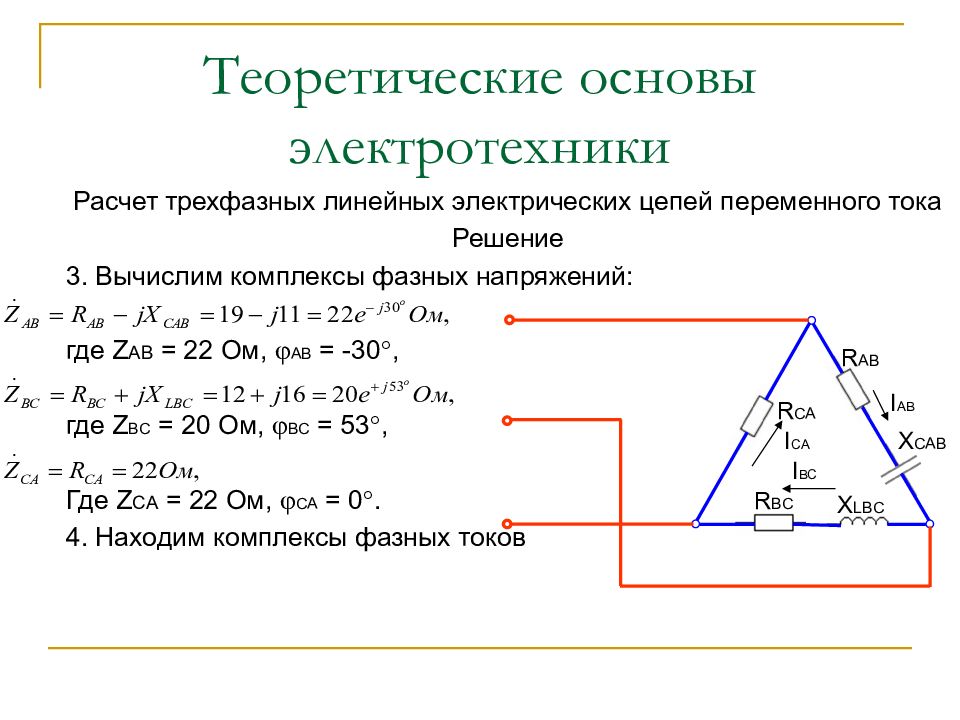
Слайд 47: Теоретические основы электротехники
Расчет трехфазных линейных электрических цепей переменного тока Решение 3. Вычислим комплексы фазных напряжений: где Z AB = 22 Ом, АВ = -30, где Z BC = 20 Ом, ВС = 53, Где Z CA = 22 Ом, СА = 0. 4. Находим комплексы фазных токов R AB X CAB R BC X LBC R CA I AB I BC I CA
Слайд 48: Теоретические основы электротехники
Расчет трехфазных линейных электрических цепей переменного тока Решение 4. Находим комплексы фазных токов модуль I AB = 17,27 A, AB = 30, модуль I ВС = 19 A, BC = -173, модуль I CA = 17,27 A, СА = 120. R AB X CAB R BC X LBC R CA I AB I BC I CA
Слайд 49: Теоретические основы электротехники
Расчет трехфазных линейных электрических цепей переменного тока Решение 5. Находим линейные токи из уравнений, записанных по первому закону Кирхгофа для узлов А, В, С: R AB X CAB R BC X LBC R CA I AB I BC I CA I A I B I C A B C
Слайд 50: Теоретические основы электротехники
Расчет трехфазных линейных электрических цепей переменного тока Решение 6. Вычисляем мощность каждой фазы и всей цепи
Слайд 51: Теоретические основы электротехники
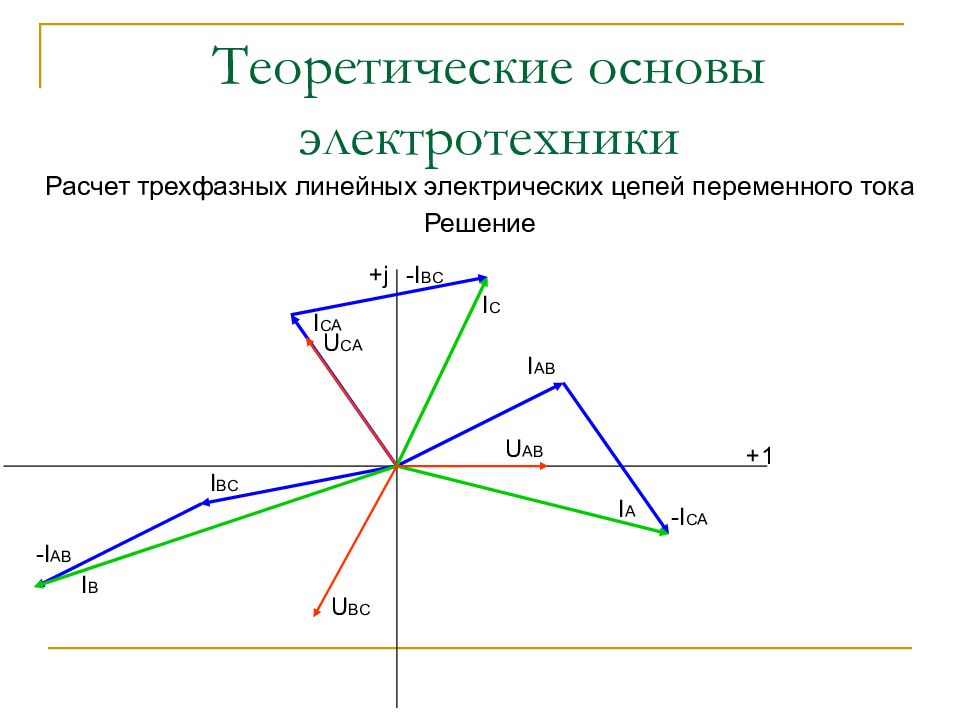
Расчет трехфазных линейных электрических цепей переменного тока Решение 7. Строим в масштабе векторную диаграмму напряжений и токов. Выбираем масштабы напряжений и токов: Mu = 100 B/c м, Mi = 4 A/c м. Векторы фазных токов I AB, I BC, I CA строим под углами АВ, ВС, СА к действительной оси. К концам векторов I AB, I BC, I CA пристраиваем отрицательные фазные токи согласно уравнениям: Замыкающие векторные треугольники векторов I AB, I BC, I CA представляют в выбранном масштабе линейные токи.
Слайд 52: Теоретические основы электротехники
Расчет трехфазных линейных электрических цепей переменного тока Решение +1 + j U AB U BC U CA I AB -I CA I A I BC -I AB I B I CA -I BC I C
Слайд 53: Теоретические основы электротехники
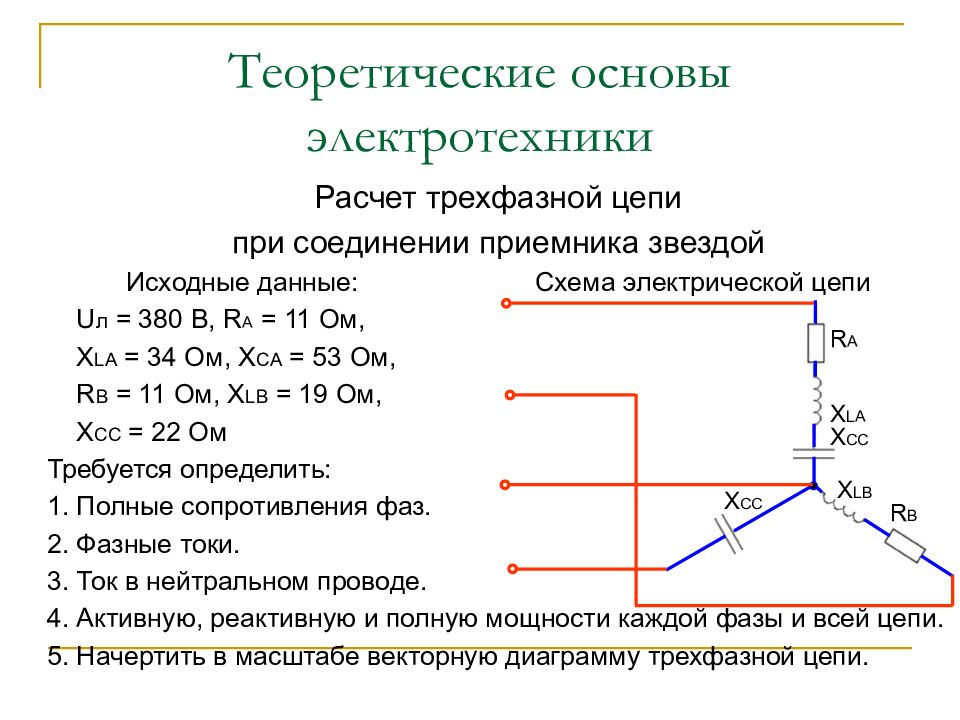
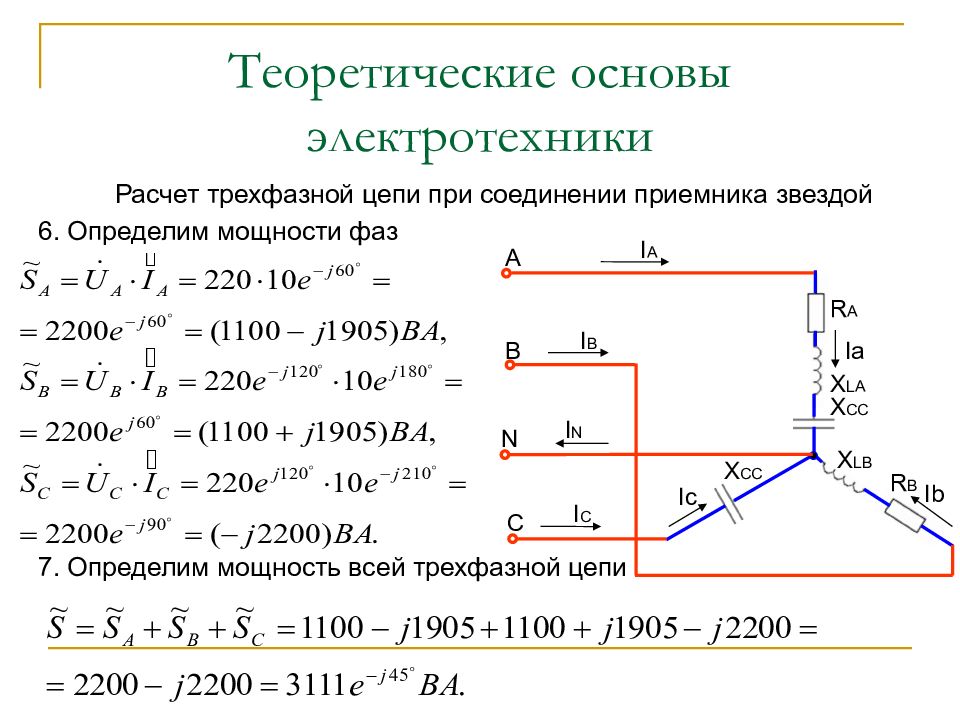
Расчет трехфазной цепи при соединении приемника звездой Исходные данные: Схема электрической цепи U л = 380 B, R A = 11 Ом, X LA = 34 Ом, X CA = 53 Ом, R B = 11 Ом, X LB = 19 Ом, X CC = 22 Ом Требуется определить: 1. Полные сопротивления фаз. 2. Фазные токи. 3. Ток в нейтральном проводе. 4. Активную, реактивную и полную мощности каждой фазы и всей цепи. 5. Начертить в масштабе векторную диаграмму трехфазной цепи. R A X LA X CC X LB R B X CC
Слайд 54: Теоретические основы электротехники
Расчет трехфазной цепи при соединении приемника звездой 1. Определим фазные напряжения трехфазной цепи U А = U В = U С = U ф = U л / 1,73 = 380 / 1,73 = 220 B. 2. Выразим в комплексной форме фазные напряжения 3. Выразим сопротивления фаз в комплексной форме
Слайд 55: Теоретические основы электротехники
Расчет трехфазной цепи при соединении приемника звездой 4. Определим комплексы фазных токов 5. Определим ток в нейтральном проводе R A X LA X CC X LB R B X CC A B C N I N I A I B I C Ia Ib Ic
Слайд 56: Теоретические основы электротехники
Расчет трехфазной цепи при соединении приемника звездой 6. Определим мощности фаз 7. Определим мощность всей трехфазной цепи R A X LA X CC X LB R B X CC A B C N I N I A I B I C Ia Ib Ic
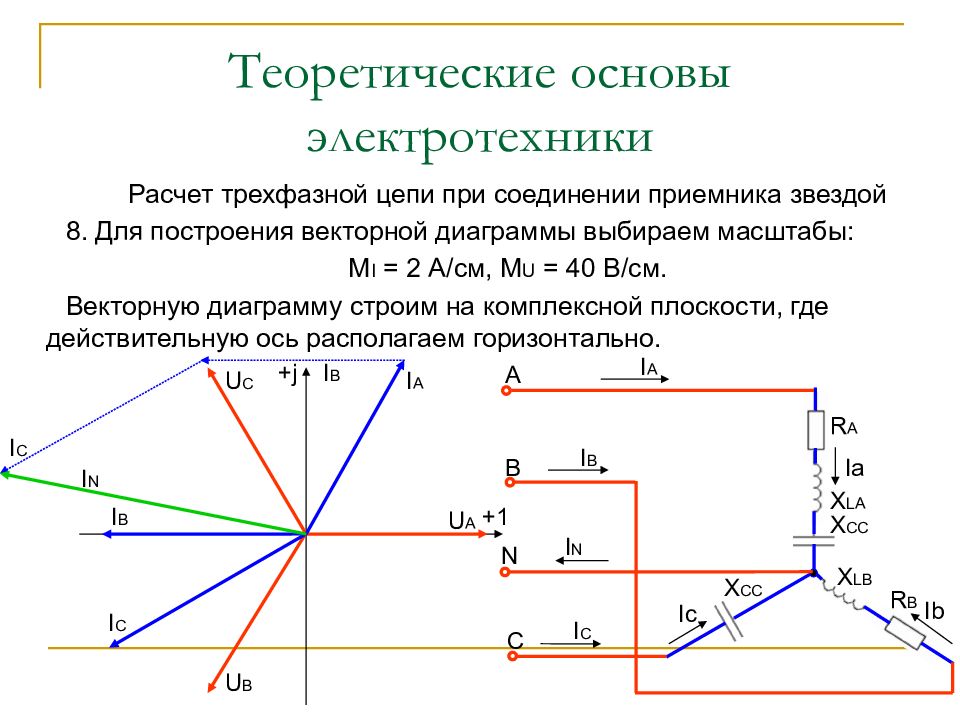
Слайд 57: Теоретические основы электротехники
Расчет трехфазной цепи при соединении приемника звездой 8. Для построения векторной диаграммы выбираем масштабы: М I = 2 А/см, М U = 40 В/см. Векторную диаграмму строим на комплексной плоскости, где действительную ось располагаем горизонтально. R A X LA X CC X LB R B X CC A B C N I N I A I B I C Ia Ib Ic +1 + j U A U B U C I A I B I C I B I C I N
Слайд 58: Теоретические основы электротехники
Последовательность и методика выполнения задачи №5 по курсовой работе
Слайд 59: Теоретические основы электротехники
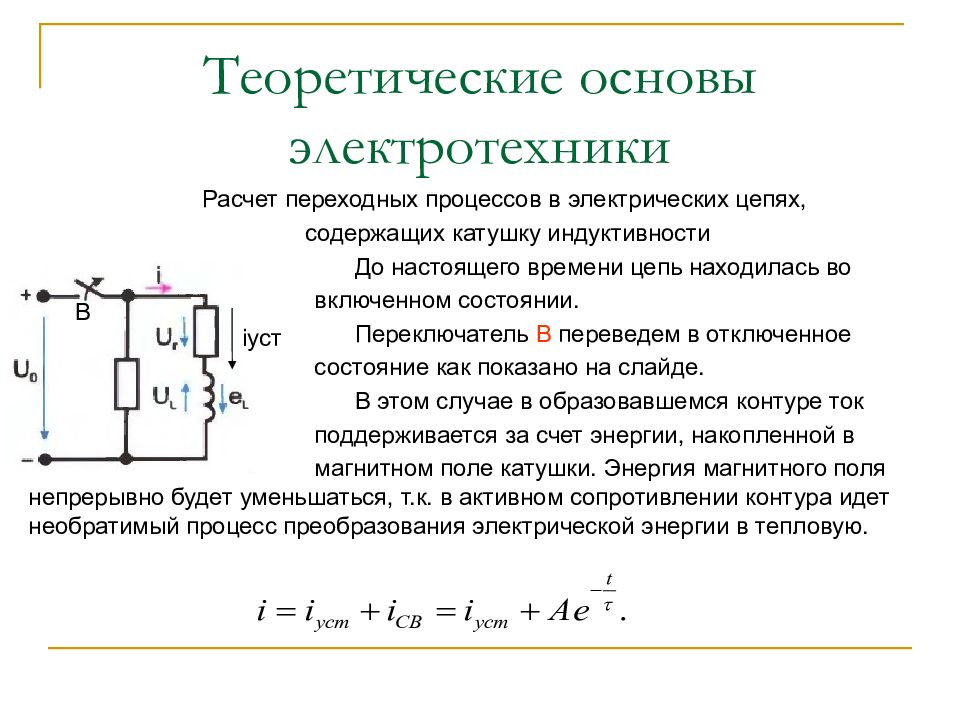
Расчет переходных процессов в электрических цепях, содержащих катушку индуктивности Дано: Электрическая схема U = 60 В, R = 10 Ом, Rp = 10 Ом, L = 200 мГн. Требуется: 1. Определить закон изменения тока и ЭДС самоиндукции в цепи 2. Определить практическую длительность переходного процесса и энергию магнитного поля при t = 3 .
Слайд 60: Теоретические основы электротехники
Расчет переходных процессов в электрических цепях, содержащих катушку индуктивности Решение 1. Определим установившееся значение тока после коммутации (замыкании ключа В) i = I = U / R = 60 / 10 = 10 A. 2. Запишем уравнение изменения тока при включении катушки Для определения постоянной интегрирования полагаем t = 0, тогда уравнение примет вид: i o = i уст + A, значит А = i o – i уст = 0 – I, или A = -I. Подставляя соответствующие значения в исходное уравнение, будем иметь i уст В
Слайд 61: Теоретические основы электротехники
Расчет переходных процессов в электрических цепях, содержащих катушку индуктивности 3. Находим постоянную времени переходного процесса = L / R = 200 / (1000 •10 ) = 0,02 c. 4. Практическая длительность переходного процеса составит t = 5 = 5 •0,02 = 0,1 c. 5. Для построения графика переходного тока задаемся моментами времени: t = 0; t = ; t = 2 ; t = 3 ; t = 4 ; t = 5 . По полученному уравнению для заданных моментов времени рассчитываем значения токов и данные расчета сводим в таблицу 5.1. Пример расчета для t = 3 . i уст В
Слайд 62: Теоретические основы электротехники
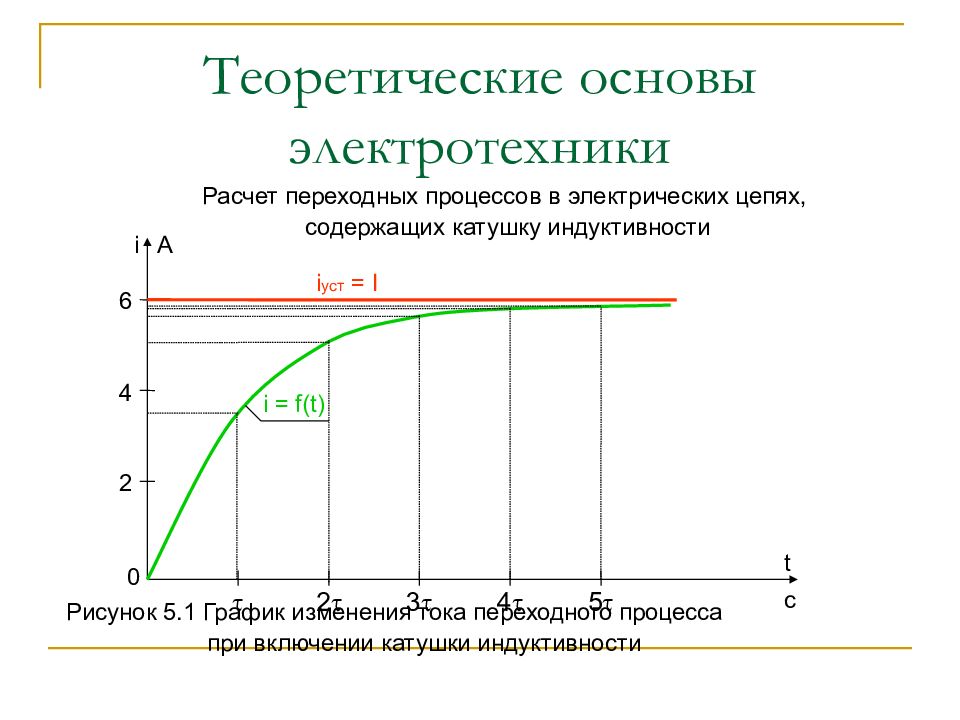
Расчет переходных процессов в электрических цепях, содержащих катушку индуктивности Таблица 5.1 Значения переходных токов в катушке индуктивности Для построения графика изменения тока принимаем масштабы М i = 1 А/см, М t = 0,5 = 0,01 с/см. t,c 0 = 0,02 2 3 4 5 i,A 0 3,79 5,19 5,70 5,89 5,96 t,c 0 = 0,02 2 3 4 5 i,A 0 3,79 5,19 5,70 5,89 5,96
Слайд 63: Теоретические основы электротехники
Расчет переходных процессов в электрических цепях, содержащих катушку индуктивности Рисунок 5.1 График изменения тока переходного процесса при включении катушки индуктивности t c i A 2 4 6 2 3 4 5 i уст = I i = f(t) 0
Слайд 64: Теоретические основы электротехники
Расчет переходных процессов в электрических цепях, содержащих катушку индуктивности Закон изменения ЭДС самоиндукции переходного процесса получим из формулы для ЭДС Для данных нашего примера По полученному уравнению для заданных моментов времени рассчитываем значения ЭДС и данные расчета сводим в таблицу 5.2. Пример расчета для t = 3 .
Слайд 65: Теоретические основы электротехники
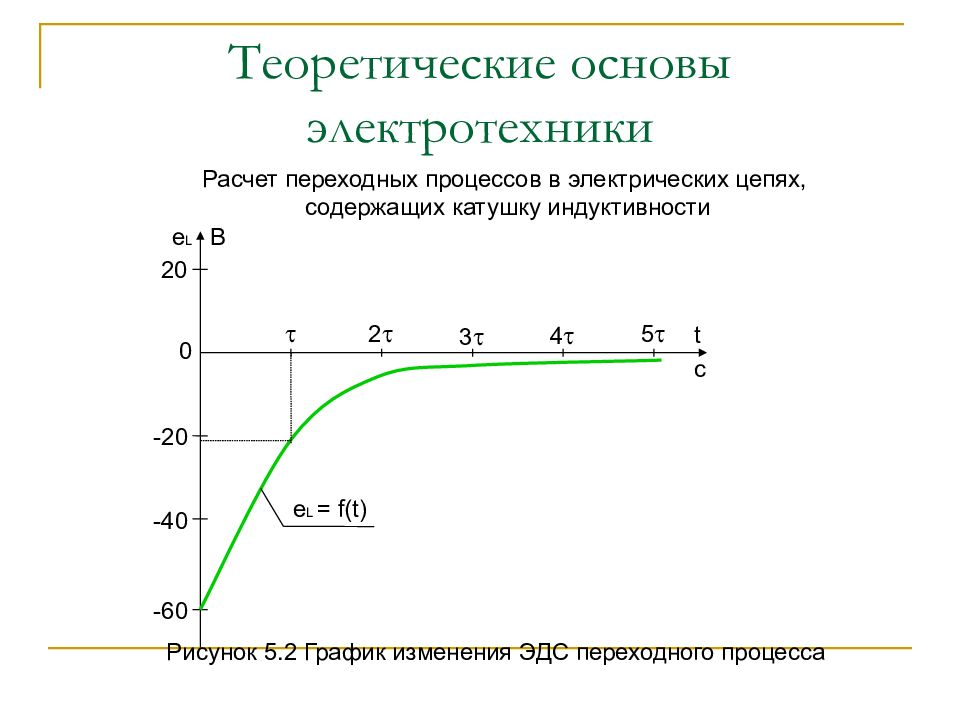
Расчет переходных процессов в электрических цепях, содержащих катушку индуктивности Таблица 5.2 Значения переходных ЭДС в катушке индуктивности Для построения графика изменения тока принимаем масштабы М e = 10 B /см, М t = 0,5 = 0,01 с/см. t,c 0 = 0,02 2 3 4 5 e,B 0 -22,02 -8,1 -2,94 -1,08 -0,42
Слайд 66: Теоретические основы электротехники
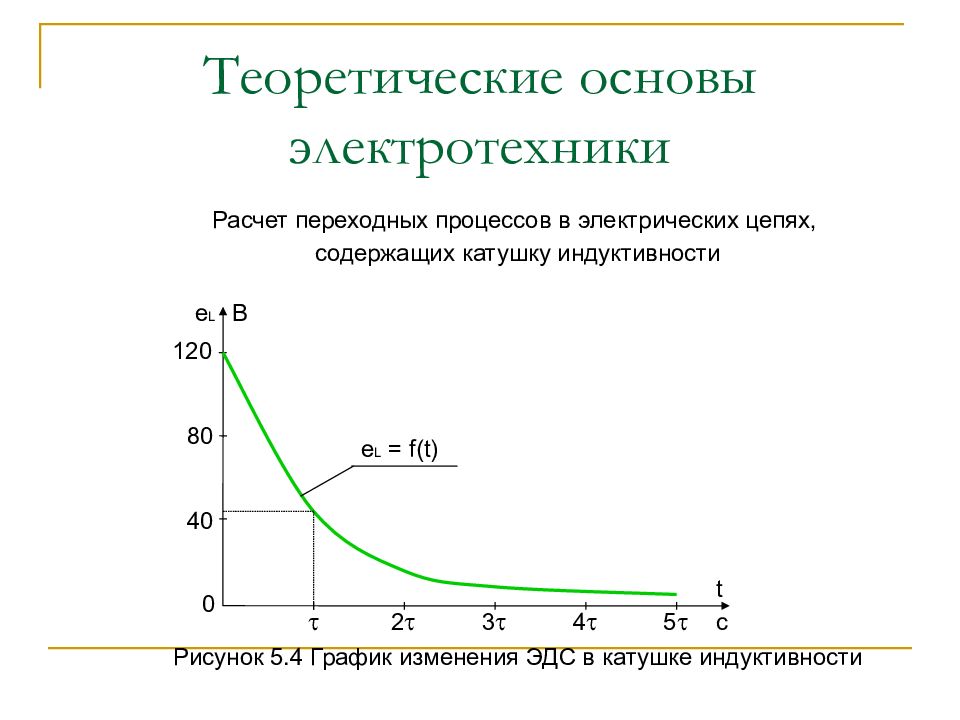
Расчет переходных процессов в электрических цепях, содержащих катушку индуктивности Рисунок 5.2 График изменения ЭДС переходного процесса t c 2 3 4 5 0 e L B 20 -20 -40 -60 e L = f(t)
Слайд 67: Теоретические основы электротехники
Расчет переходных процессов в электрических цепях, содержащих катушку индуктивности Энергию магнитного поля катушки индуктивности при t = 3 определим в соответствии со следующей формулой
Слайд 68: Теоретические основы электротехники
Расчет переходных процессов в электрических цепях, содержащих катушку индуктивности До настоящего времени цепь находилась во включенном состоянии. Переключатель В переведем в отключенное состояние как показано на слайде. В этом случае в образовавшемся контуре ток поддерживается за счет энергии, накопленной в магнитном поле катушки. Энергия магнитного поля непрерывно будет уменьшаться, т.к. в активном сопротивлении контура идет необратимый процесс преобразования электрической энергии в тепловую. i уст В
Слайд 69: Теоретические основы электротехники
Расчет переходных процессов в электрических цепях, содержащих катушку индуктивности Так как при отключении цепи от источника ток в цепи будет равен нулю, значит в последнем уравнении можно записать i уст = 0. Тогда уравнение будет иметь вид где = L / (R+R p ) = 0,2 / (10+10) = 0,01 c – постоянная времени переходного процесса. Определим постоянную интегрирования, полагая t = 0 и учитывая, что согласно первому закону коммутации ток в первый момент коммутации будет таким, каким он был в последний момент до коммутации i o = A •e = A = 6 A.
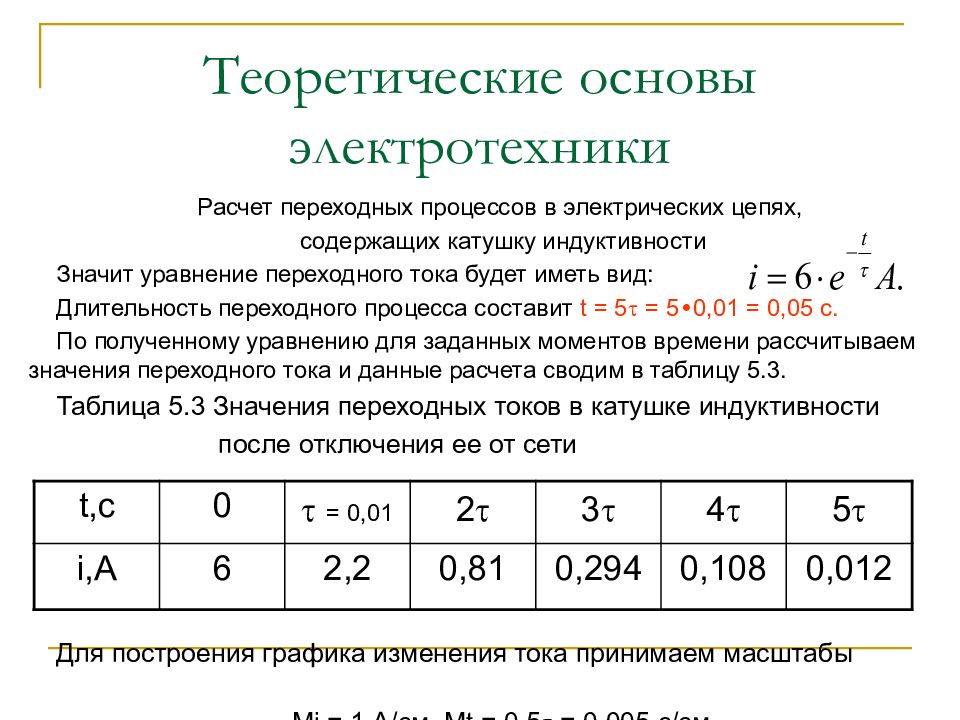
Слайд 70: Теоретические основы электротехники
Расчет переходных процессов в электрических цепях, содержащих катушку индуктивности Значит уравнение переходного тока будет иметь вид: Длительность переходного процесса составит t = 5 = 5 • 0,01 = 0,05 c. По полученному уравнению для заданных моментов времени рассчитываем значения переходного тока и данные расчета сводим в таблицу 5.3. Таблица 5.3 Значения переходных токов в катушке индуктивности после отключения ее от сети Для построения графика изменения тока принимаем масштабы М i = 1 А/см, М t = 0,5 = 0,0 05 с/см. t,c 0 = 0,0 1 2 3 4 5 i,A 6 2,2 0,81 0,294 0,108 0,012
Слайд 71: Теоретические основы электротехники
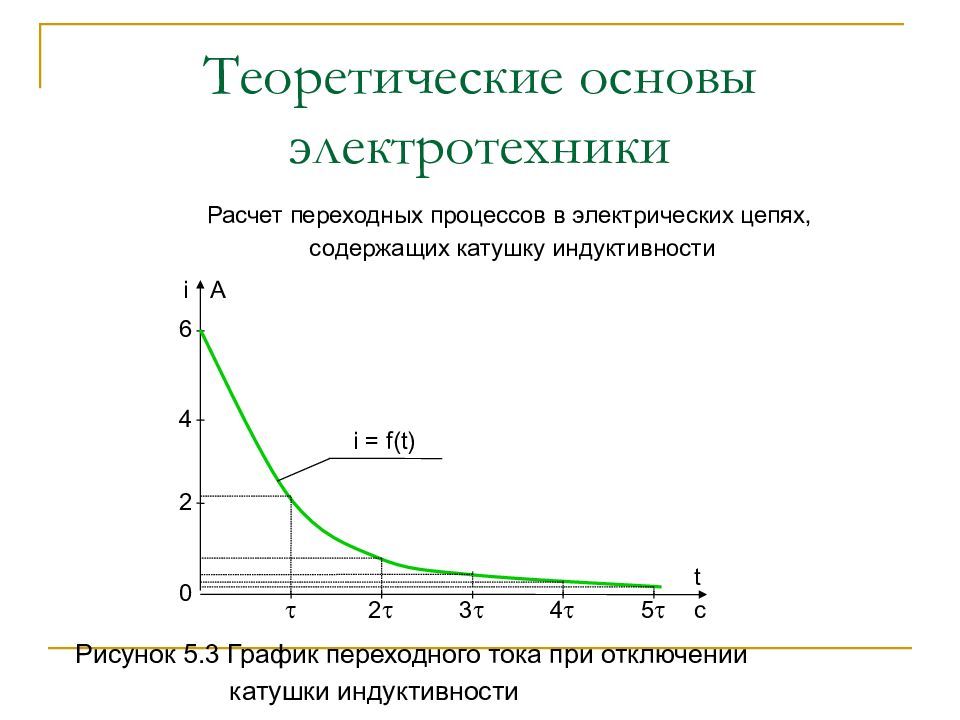
Расчет переходных процессов в электрических цепях, содержащих катушку индуктивности Рисунок 5.3 График переходного тока при отключении катушки индуктивности t c 2 3 4 5 0 2 4 6 i A i = f(t)
Слайд 72: Теоретические основы электротехники
Расчет переходных процессов в электрических цепях, содержащих катушку индуктивности В соответствии с законом изменения ЭДС самоиндукции будем иметь В рассматриваемом случае По полученному уравнению для заданных моментов времени рассчитываем значения переходной ЭДС и данные расчета сводим в таблицу 5.4
Слайд 73: Теоретические основы электротехники
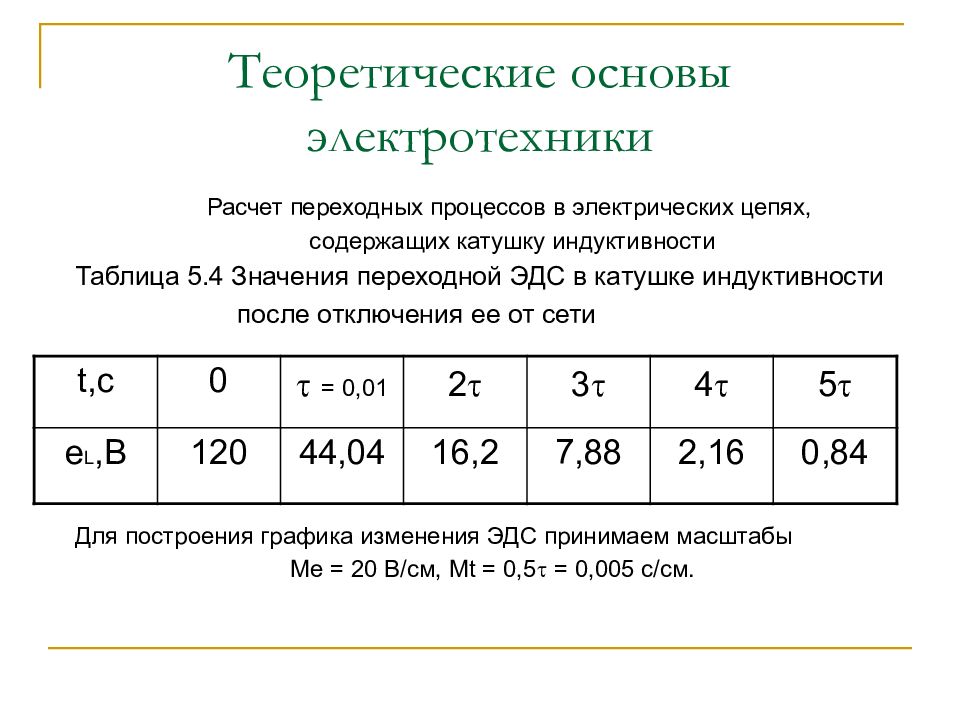
Расчет переходных процессов в электрических цепях, содержащих катушку индуктивности Таблица 5.4 Значения переходной ЭДС в катушке индуктивности после отключения ее от сети Для построения графика изменения ЭДС принимаем масштабы Ме = 20 В/см, М t = 0,5 = 0,0 05 с/см. t,c 0 = 0,0 1 2 3 4 5 е L, В 120 44,04 16,2 7,88 2,16 0,84
Слайд 74: Теоретические основы электротехники
Расчет переходных процессов в электрических цепях, содержащих катушку индуктивности Рисунок 5.4 График изменения ЭДС в катушке индуктивности t c 2 3 4 5 0 40 80 120 e L B e L = f(t)
Слайд 75: Теоретические основы электротехники
Расчет переходных процессов в электрических цепях, содержащих конденсатор Дано: Электрическая схема R = 2 Ом, C = 10 мкФ, Rp = 8 Ом, U = 50 B. Требуется: 1. Определить законы изменения переходных напряжений и тока при заряде конденсатора и построить их графики. 2. Определить законы изменения переходных напряжений и тока при разряде конденсатора и построить их графики. 3. Определить практическую длительность заряда и разряда конденсатора и энергию электрического поля при t = 3 . + - 1 2 В R C U i з ip u c
Слайд 76: Теоретические основы электротехники
Расчет переходных процессов в электрических цепях, содержащих конденсатор При переводе выключателя В в положение 1 происходит заряд конденсатора С через сопротивление R. Постоянная времени заряда конденсатора составит: На основании второго закона коммутации получены уравнения, характеризующие напряжение и ток при заряде конденсатора где U – напряжение источника, u уст = U – напряжение на конденса- торе после зарядки, u св – свободная составляющая напряжения на конденсаторе. + - 1 2 В R C U i з ip u c
Слайд 77: Теоретические основы электротехники
Расчет переходных процессов в электрических цепях, содержащих конденсатор Вычисляем значения напряжения на конденсаторе при его заряде для значений времени: t = 0, , 2, 3, 4, 5. Определим значение напряжения для t = 3. Для остальных значений времени рассчитываем напряжение аналогично и данные сводим в таблицу 5,5. Таблица 5.5 Значения переходного напряжения на емкости t,c 0 = 20 2 3 4 5 Uc,B 0 31,6 43,23 47,51 49,08 49,66
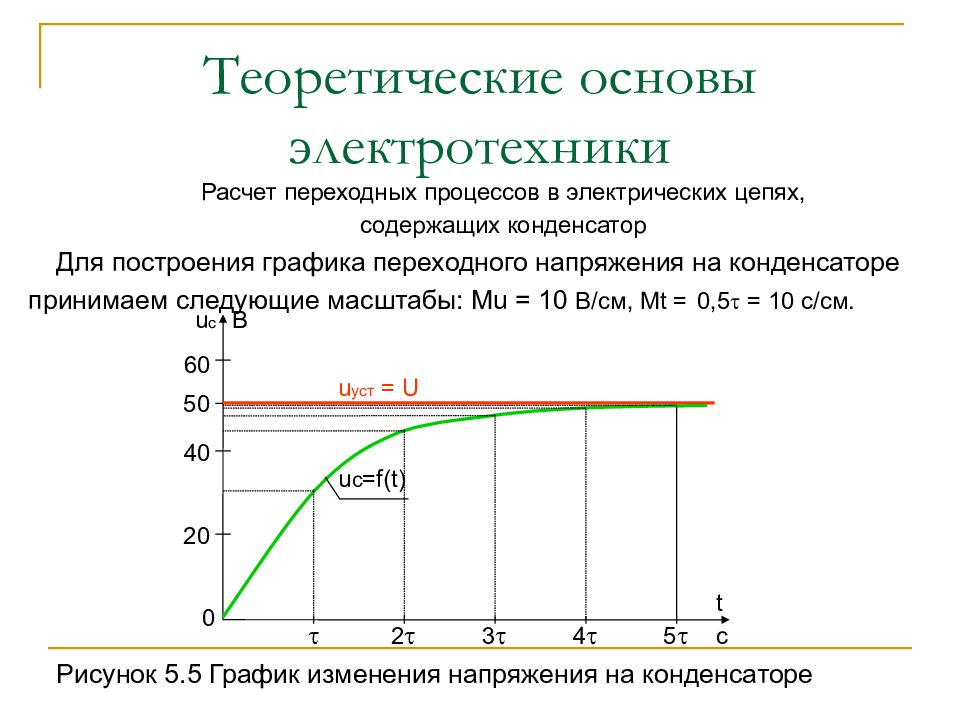
Слайд 78: Теоретические основы электротехники
Расчет переходных процессов в электрических цепях, содержащих конденсатор Для построения графика переходного напряжения на конденсаторе принимаем следующие масштабы: М u = 10 В/см, М t = 0,5 = 10 с/см. Рисунок 5.5 График изменения напряжения на конденсаторе t c 2 3 4 5 0 20 40 60 u c B 50 u уст = U u c =f(t)
Слайд 79: Теоретические основы электротехники
Расчет переходных процессов в электрических цепях, содержащих конденсатор Аналогично вычисляем значения зарядного тока согласно закону изменения переходного тока при заряде конденсатора для значений времени: t = 0, , 2, 3, 4, 5. Результаты расчетов сводим в таблицу 5,6. Таблица 5.6 Значения переходного тока в конденсаторе t,c 0 = 20 2 3 4 5 i, мкА 25 9,19 3,38 1,24 0,46 0,17
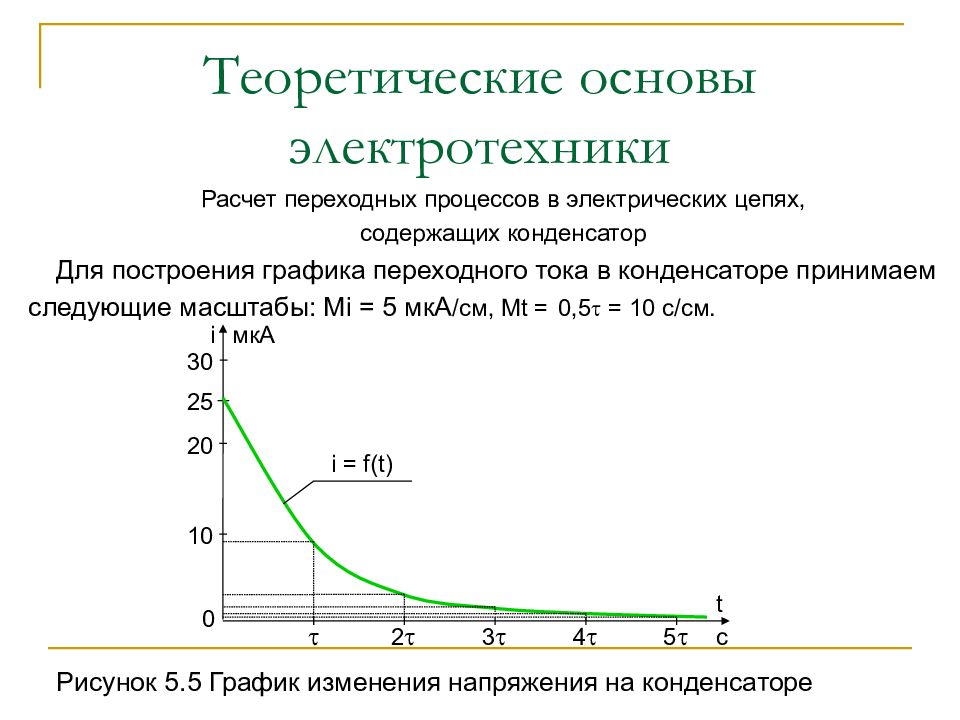
Слайд 80: Теоретические основы электротехники
Расчет переходных процессов в электрических цепях, содержащих конденсатор Для построения графика переходного тока в конденсаторе принимаем следующие масштабы: М i = 5 мкА /см, М t = 0,5 = 10 с/см. Рисунок 5.5 График изменения напряжения на конденсаторе t c 2 3 4 5 0 10 20 30 25 i мкА i = f(t)
Слайд 81: Теоретические основы электротехники
Расчет переходных процессов в электрических цепях, содержащих конденсатор
Слайд 82: Теоретические основы электротехники
Расчет переходных процессов в электрических цепях, содержащих конденсатор