Волновая функция и ее физический смысл. Уравнение Шредингера – основное уравнение квантовой механики. Соотношение неопределенностей Гейзенберга.
Представление Бора об определенных орбитах, по которым движутся электроны в атоме, оказалось весьма условным. На самом деле движение электрона в атоме очень мало похоже на движение планет или спутников. Классическая механика не могла правильно описать поведение микрочастиц. Необходимо было создать механику микрочастиц, которая учитывала бы их волновые свойства.
Новая механика получила название квантовой механики. Ее основы были заложены Шредингером, Гейзенбергом, Дираком и др. Необходимость вероятностного подхода к описанию микрообъектов является важнейшей особенностью квантовой теории. В квантовой механике для характеристики состояний объектов в микромире вводится понятие волновой функции Ψ (пси-функции). Она является функцией координат и времени. ( х, у, z, t )
Физический смысл волновой функции сформулировал Борн в 1926 году. Согласно Борну: квадрат модуля волновой функции |Ψ| 2 определяет вероятность dP нахождения микрочастицы в пределах объема dV пространства: (1) где A – коэффициент пропорциональности, Ψ - функция, комплексно сопряженная с Ψ.
Таким образом, величина |Ψ| 2 имеет смысл плотности вероятности нахождения частицы в соответствующем месте пространства. Иными словами она определяет интенсивность волн де Бройля.
Из определения волновой функции следует, что она должна удовлетворять условию нормировки вероятностей: Это означает, что пребывание частицы где-либо в пространстве есть достоверное событие и его вероятность должна быть равна единице. (2)
Свойства волновой функции: 1. Ψ – функцию можно умножить на произвольное комплексное число C, тогда функции Ψ и C Ψ определяют одно и тоже состояние квантовой частицы. 2. Волновая функция подчиняется принципу суперпозиции. Суть этого принципа заключается в следующем. Пусть волновая функция 1 описывает одно состояние квантовомеханической системы (частицы), а функция 2 – второе состояние. Тогда всегда существует состояние системы, описываемое функцией: = С 1 1 + С 2 2 где С 1 и С 2 произвольные комплексные числа.
Принцип суперпозиции в квантовой механике существенно отличается от суперпозиции в классической физике. Например, суперпозиция двух волн в классической физике дает новую волну, которая имеет конкретные характеристики (амплитуда, фаза и т.д.), в квантовой механике суперпозиция характеризуется неопределенностью результатов измерений.
Рассмотрим например, совокупность собственных значений некоторой физической величины q i и соответствующих им собственных функций i. В каждом состоянии величина q имеет определенное значение: в состоянии 1 – значение q 1, в состоянии 2 – значение q 2 и т.д. Согласно принципу суперпозиции возможное состояние описывается функцией: = С 1 1 + С 2 2
В этом состоянии величина q не будет иметь определенного значения. Она может принимать значения либо q 1, либо q 2. Вероятности получения этих значений равны квадратам модулей коэффициентов С - С 1 2 и С 2 2.
3. Согласно пункту 2 пси-функцию любого состояния можно разложить по собственным функциям, т.е. представить в виде: (3)
Для состояния, изменяющегося со временем, коэффициент С n зависит от времени t. Квадраты модулей коэффициентов С n дают вероятность того, что при измерениях, производимых над системой, находящейся в состоянии , будут получены соответствующие значения некоторой величины q. Поскольку сумма всех таких вероятностей должна быть равна единице, коэффициенты С n должны удовлетворять условию:
Это условие всегда выполняется для нормированной волновой функции. Таким образом, волновая функция является одной из основных величин, описывающей поведение квантовой частицы, которое имеет вероятностный характер. Волновая функция Ψ является решением основного уравнения квантовой механики – уравнения Шредингера.
Подобно тому, как уравнения динамики Ньютона не могут быть получены теоретически, а являются обобщением большого числа экспериментальных данных, уравнение Шредингера также нельзя вывести из каких-либо известных ранее соотношений. Его следует рассматривать как исходное основное предположение, справедливость которого доказывается тем, что вытекающие из него следствия согласуются с опытными фактами.
Основное уравнение нерелятивистской ( υ << c ) квантовой механики было получено Шредингером в 1926 году: (4) где Ψ = Ψ( x, y, z, t ) – искомая волновая функция, ħ = h /2π – постоянная Планка, i – мнимая единица, m – масса частицы, U – потенциальная энергия частицы в силовом поле, где частица движется.
2 – оператор Лапласа, действие которого на волновую функцию представляет собой сумму вторых частных производных по координатам: Уравнение (4) называется временным уравнением Шредингера.
Вид волновой функции Ψ, как следует из (4), определяется потенциальной энергией частицы U, т.е. характером тех сил, которые действуют на частицу. Потенциальная энергия частицы есть функция координат и времени, т.е. U = U ( x, y, z, t ). Если U не зависит от времени, т.е. U = U ( x, y, z ) (стационарное поле), то волновая функция Ψ может быть представлена в виде произведения: (5)
В (5) волновая функция Ψ зависит только от координат Ψ = Ψ( x, y, z ), а второй сомножитель зависит только от времени t, E – полная энергия частицы, которая в случае стационарного поля остается постоянной ( E = const ). Подставим (5) в (4): Сокращая на общий множитель, получим:
Раскроем скобки: или
Последнее уравнение обычно записывают в виде: (6) (6) – уравнение Шредингера для стационарных состояний ( стационарное уравнение Шредингера ). Стационарные состояния – это такие состояния, в которых все наблюдаемые физические параметры не меняются с течением времени.
Конкретный вид волновой функции Ψ определяется внешними условиями, в которых находится микрочастица. Математический аппарат квантовой механики позволяет находить волновую функцию частицы, находящейся в заданных силовых полях.
Уравнение Шредингера дополняется важными условиями, которые накладываются на волновую функцию: 1. Функция Ψ должна быть непрерывной, конечной и однозначной. 2. Производные Ψ – функции по координатам и времени должны быть непрерывны. 3. Функция |Ψ| 2 должна быть интегрируема. Решение уравнения Шредингера для электрона в атоме водорода (или в водородоподобной системе) позволило получить важные результаты.
Оказалось, что состояние электрона в атоме характеризуется целым набором квантовых чисел. Главное квантовое число n определяет квантование энергии атома. Для квантования момента импульса электрона в атоме вводится так называемое орбитальное квантовое число l. Проекция момента импульса на любое выделенное в пространстве направление (например, направление вектора индукции магнитного поля) также принимает дискретный ряд значений. Для квантования проекции момента импульса вводится магнитное квантовое число m (не путать с массой ).
Квантовые числа n, l, m связаны определенными правилами квантования. Например, орбитальное квантовое число l может принимать целочисленные значения от 0 до ( n – 1). Магнитное квантовое число m может принимать любые целочисленные значения в интервале ± l. Таким образом, каждому значению главного квантового числа n, определяющему энергетическое состояние атома, соответствует целый ряд комбинаций квантовых чисел l и m. Каждой такой комбинации соответствует определенное распределение вероятности |Ψ| 2 обнаружения электрона в различных точках пространства.
Поэтому в квантовой физике электрон рассматривается не как «шарик», а как какое-то «электронное облако», плотность которого определяет вероятность нахождения электрона в том или ином месте объема атома. Состояния, в которых орбитальное квантовое число l =0, описываются сферически симметричными распределениями вероятности. Они называются s -состояниями (1 s, 2 s,..., ns,...). При значениях l > 0 сферическая симметрия электронного облака нарушается. Состояния с l =1 называются p -состояниями, с l =2 – d -состояниями и т. д.
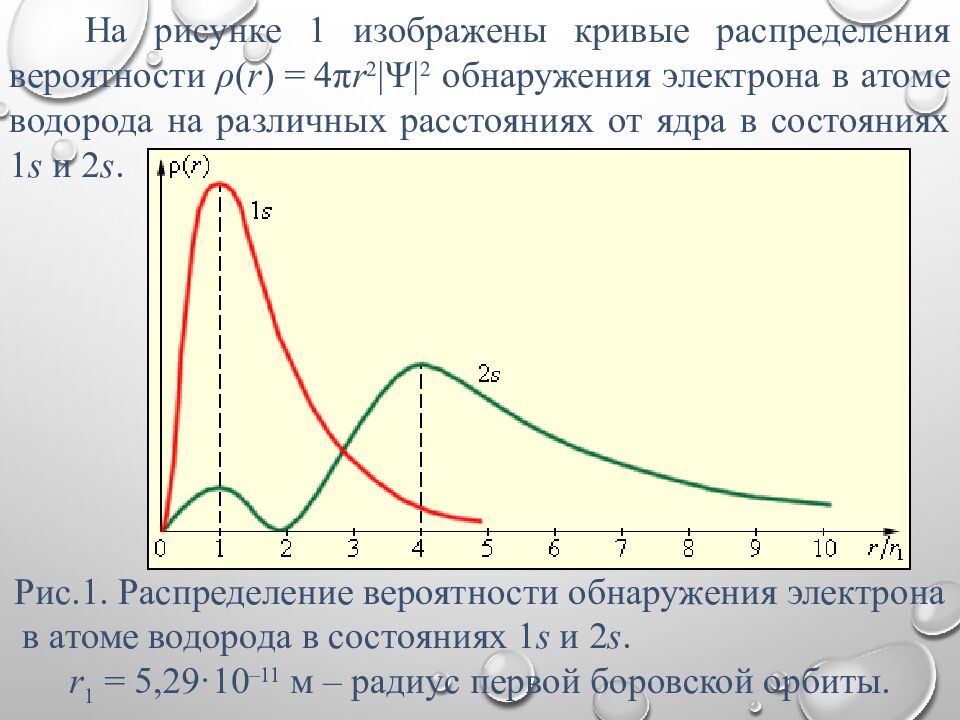
На рисунке 1 изображены кривые распределения вероятности ρ ( r ) = 4π r 2 |Ψ| 2 обнаружения электрона в атоме водорода на различных расстояниях от ядра в состояниях 1 s и 2 s. Рис.1. Распределение вероятности обнаружения электрона в атоме водорода в состояниях 1 s и 2 s. r 1 = 5,29·10 –11 м – радиус первой боровской орбиты.
Как видно из рисунка 1, электрон в состоянии 1 s (основное состояние атома водорода) может быть обнаружен на различных расстояниях от ядра. С наибольшей вероятностью его можно обнаружить на расстоянии, равном радиусу r 1 первой боровской орбиты. Вероятность обнаружения электрона в состоянии 2 s максимальна на расстоянии r = 4 r 1 от ядра. В обоих случаях атом водорода можно представить в виде сферически симметричного электронного облака, в центре которого находится ядро.
В классической механике состояние материальной точки (частицы) в каждый момент времени характеризуется ее положением (координатами) и импульсом (скоростью). Реальные микрочастицы – электроны, протоны, атомы и др. – более сложные объекты. Нельзя характеризовать мгновенное состояние микрочастицы точными значениями ее координат и импульса. Причина этого в том, что всякая микрочастица проявляет и корпускулярные и волновые свойства.
Таким образом, на законы классической механики наложены определенные ограничения при описании движения микрочастиц. Одним из таких ограничений является соотношение неопределенностей Гейзенберга. Его можно получить рассмотрев дифракцию электронов на щели.
С точки зрения волновой теории, максимумы в картине дифракции электронов соответствуют наибольшей интенсивности волн де Бройля. В области максимумов, зарегистрированных на фотопластинке, попадает большое число электронов. Но процесс попадания электронов в различные места на фотопластинке не индивидуален. Принципиально невозможно предсказать, куда попадет очередной электрон после рассеяния, существует лишь определенная вероятность попадания электрона в то или иное место.
Дифракционные явления проявляются наиболее отчетливо, когда размеры препятствия, на котором происходит дифракция волн, соизмеримы с длиной волны. Это относится к волнам любой физической природы. Для волн де Бройля естественной дифракционной решеткой является упорядоченная структура кристалла с пространственным периодом порядка размеров атома ( 0,1 нм). Препятствие таких размеров (например, отверстие в непрозрачном экране) невозможно создать искусственно, но для уяснения природы волн де Бройля можно ставить мысленные эксперименты.
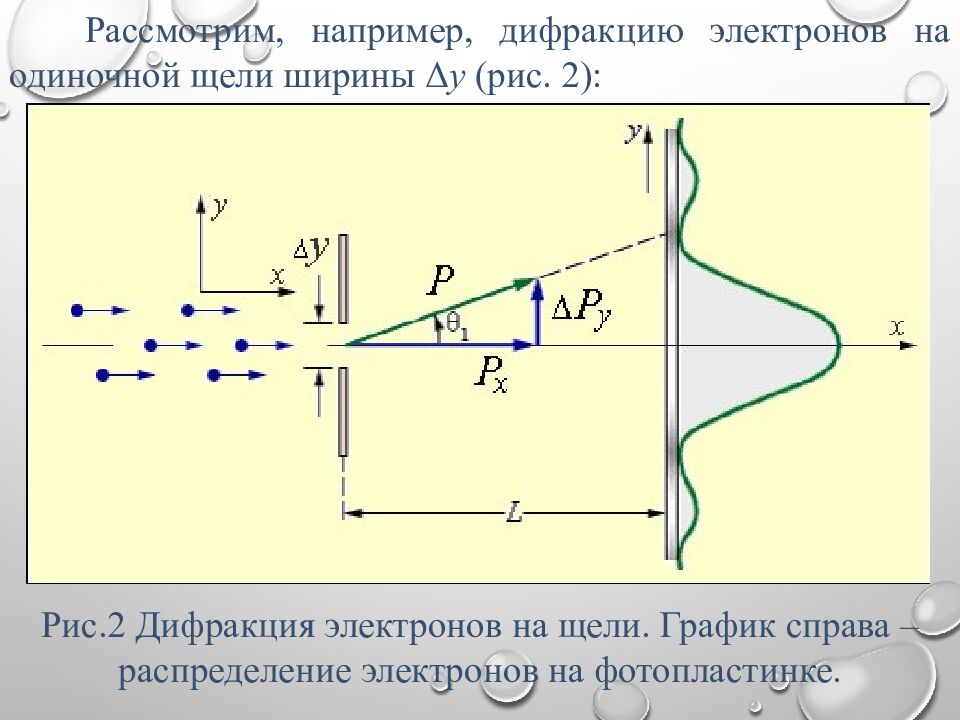
Рассмотрим, например, дифракцию электронов на одиночной щели ширины Δ y (рис. 2): Рис.2 Дифракция электронов на щели. График справа – распределение электронов на фотопластинке.
Более 85% всех электронов, прошедших через щель, попадут в центральный дифракционный максимум. Угловая полуширина θ 1 этого максимума находится из условия минимума при дифракции на щели: Δ y sin θ 1 = kλ k = 1 – первый минимум. Тогда: Δ y sin θ 1 = λ Или: Это формула волновой теории.
С корпускулярной точки зрения можно считать, что при пролете через щель электрон приобретает дополнительный импульс в перпендикулярном направлении. Пренебрегая 15 % электронов, которые попадают на фотопластинку за пределами центрального максимума, можно считать, что максимальное значение Δ P y поперечного импульса равно: где P = h / λ – модуль полного импульса электрона, согласно де Бройлю, h – постоянная Планка, λ – длина волны де Бройля. Величина P при прохождении электрона через щель не меняется, т. к. остается неизменной длина волны λ.
Из этих соотношений следует: Квантовая механика вкладывает в это простое на вид соотношение, являющееся следствием волновых свойств микрочастицы, чрезвычайно глубокий смысл. Прохождение электронов через щель является экспериментом, в котором y – координата электрона – определяется с точностью Δ y. Величину Δ y называют неопределенностью измерения координаты.
В то же время точность определения y – составляющей импульса электрона в момент прохождения через щель – равна Δ P y или даже больше, если учесть побочные максимумы дифракционной картины. Эту величину называют неопределенностью проекции импульса. Таким образом, величины Δ y и Δ P y связаны соотношением: Δ y Δ P y ≥ h
Такие же соотношения можно записать и для координат x и z : (7) Соотношение (7) называется соотношением (принципом) неопределенностей Гейзенберга для координат и импульса.
Величины Δ y и Δ P y нужно понимать в том смысле, что микрочастицы в принципе не имеют одновременно точного значения координаты и соответствующей проекции импульса. Соотношение неопределенностей не связано с несовершенством применяемых приборов для одновременного измерения координаты и импульса микрочастицы. Оно является проявлением двойственной корпускулярно-волновой природы материальных микрообъектов.
Используя связь между импульсом и энергией частицы ( E = P c ) можно показать, что: (8) Соотношение (8) называется соотношением неопределенностей Гейзенберга для энергии и времени.
Соотношение (8) означает, что чем короче время существования какого-то состояния или время, отведенное для его наблюдения, тем с меньшей определенностью можно говорить об энергии этого состояния. И наоборот, чем больше это время, тем с большей точностью определена энергия состояния. Если состояние стационарно, то оно может существовать бесконечно долго. Именно по этой причине энергия стационарного состояния имеет вполне определенное значение.
Соотношение неопределенностей (7) позволяет оценить, в какой мере можно применять к микрочастицам понятия классической механики. Оно показывает, в частности, что к микрообъектам неприменимо классическое понятие траектории, так как движение по траектории характеризуется в любой момент времени определенными значениями координат и скорости. Принципиально невозможно указать траекторию, по которой двигался какой-то конкретный электрон после прохождения щели до фотопластинки в рассмотренном мысленном эксперименте.
Однако, при определенных условиях соотношение неопределенностей не противоречит классическому описанию движения тел, в том числе и микрочастиц. Например, электронный пучок в кинескопе телевизора при вылете из электронной пушки имеет диаметр Δ y порядка 10 –3 см. В современном телевизоре ускоряющее напряжение U ≈ 15 кВ. Легко подсчитать импульс электрона: P = 6,6 10 -23 кг м/с. Этот импульс направлен вдоль оси трубки.
Из соотношения неопределенностей следует, что электронам при формировании пучка сообщается неконтролируемый импульс Δ P y, перпендикулярный оси пучка: Δ P y ≈ h / Δ y ≈ 6,6 10 –29 кг м/с. Пусть до экрана кинескопа электроны пролетают расстояние L ≈ 0,5 м. Тогда размытие Δ l пятна на экране, обусловленное волновыми свойствами электрона, составит (рис.2):
Поскольку Δ l << Δ y, движение электронов в кинескопе телевизора можно рассматривать с помощью законов классической механики. Таким образом, с помощью соотношения неопределенностей можно выяснить, справедливы или нет законы классической физики в тех или иных случаях.
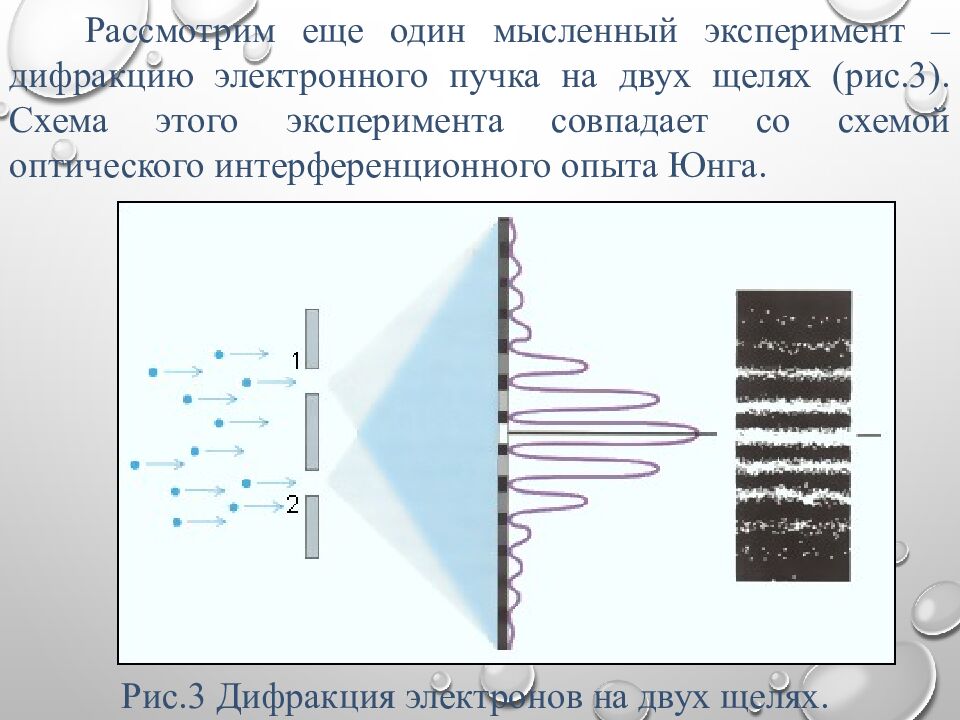
Рассмотрим еще один мысленный эксперимент – дифракцию электронного пучка на двух щелях (рис.3). Схема этого эксперимента совпадает со схемой оптического интерференционного опыта Юнга. Рис.3 Дифракция электронов на двух щелях.
Анализ этого эксперимента позволяет проиллюстрировать логические трудности, возникающие в квантовой теории. Те же проблемы возникают при объяснении оптического опыта Юнга, исходя из концепции фотонов.
Если в опыте по наблюдению дифракции электронов на двух щелях закрыть одну из щелей, то интерференционные полосы исчезнут, и фотопластинка зарегистрирует распределение электронов, продифрагировавших на одной щели (рис.2). В этом случае все электроны, долетающие до фотопластинки, проходят через единственную открытую щель. Если же открыты обе щели, то появляются интерференционные полосы, и тогда возникает вопрос, через какую из щелей пролетает тот или иной электрон ?
Психологически очень трудно смириться с тем, что ответ на этот вопрос может быть только один: электрон пролетает через обе щели. Мы интуитивно представляем себе поток микрочастиц как направленное движение маленьких шариков и применяем для описания этого движения законы классической физики. Но электрон (и любая другая микрочастица) обладает не только корпускулярными, но и волновыми свойствами.
Легко представить, как электромагнитная световая волна проходит через две щели в оптическом опыте Юнга, т. к. волна не локализована в пространстве. Но если принять концепцию фотонов, то мы должны признать, что каждый фотон тоже не локализован. Невозможно указать, через какую из щелей пролетел фотон, как невозможно проследить за траекторией движения фотона до фотопластинки и указать точку, в которую он попадет.
Опыт показывает, что даже в том случае, когда фотоны пролетают через интерферометр поштучно, интерференционная картина после пролета многих независимых фотонов все равно возникает. Поэтому в квантовой физике делается вывод: фотон интерферирует сам с собой.
Все вышесказанное относится и к опыту по дифракции электронов на двух щелях. Вся совокупность известных экспериментальных фактов может найти объяснение, если принять, что дебройлевская волна каждого отдельного электрона проходит одновременно через оба отверстия, в результате чего и возникает интерференция. Поштучный поток электронов тоже дает интерференцию при длительной экспозиции, то есть электрон, как и фотон, интерферирует сам с собой.
