Первый слайд презентации: Квантовая механика
Курс лекций по общей физики Доцент Петренко Л.Г. Кафедра общей и экспериментальной физики НТУ «ХПИ» Харьков - 2012 год Раздел 6 Основные представления квантовой физики
Представления об атомном строении вещества, возникли ещё в античные времена: 6.2.1. Трудности классической физики при объяснении строения и стабильности атома. Модели атома Томсона, Резерфорда. Демокрит 460-370 гг. до н.э. Эпикур 341-270 гг. до н.э. Лукреций Кар 99-55 гг. до н.э.
Слайд 3: В начале 18 века атомные представления постепенно стали складываться в научную теорию
Реальность существования атомов подтверждалась опытами : французского химика А.Лавуазье (1743-1794) английского химика и физика Д.Дальтона (1766-1844) российского физика, химика и философа М.В.Ломоносова (1711-1765).
Слайд 4: До конца 19 века атомы рассматривались как электрически нейтральные, неделимые частицы вещества, имеющие размеры ~10 -10 м
Эксперименты по ионизации, термоэлектронной эмиссии, фотоэффекту, по изучению спектров излучения нагретых тел показали, что атом не является неделимым, а в его состав входят заряженные частицы. В 1897 году английский физик Дж.Дж.Томсон открыл электрон. атом - непрерывно положительно заряженный шар, внутри которого около положения равновесия колеблются отрицательно заряженные электроны, образующие группы, конфигурация которых определяет периодичность свойств химических элементов. Построение модели атома в начале 20 века стало одной из важнейших научных проблем. Дж.Дж.Томсон, предложил модель «кекса» :
Слайд 5: Модель Дж.Дж.Томсона и все другие модели были опровергнуты опытами Э.Резерфорда по рассеянию веществом - частиц
Резерфорд исследовал рассеяние - частиц очень тонкой (0,1 1,0мкм) золотой фольгой. Оказалось, что подавляющее большинство - частиц практически не испытывают отклонение, и только небольшое их количество (примерно одна из 20000) отклоняется на очень большие углы - до 150 0. Многочисленные опыты показали, что такие отклонения не случайны, а закономерны.
Слайд 6: Атом содержит очень плотное ядро размером ~10 -15 м, в котором сосредоточена практически вся масса атома. Ядро имеет положительный заряд, равный +Zе ( Z – порядковый номер элемента в периодической системе). Вокруг ядра внутри области размером ~10 -10 м
Теоретический расчёт, проведенный Резерфордом на основе анализа экспериментальных данных, позволил ему в 1911 году построить планетарную модель атома : Электроны образуют электронную оболочку. по замкнутым орбитам движутся Z электронов с суммарным зарядом – Ze.
Центростремительное ускорение электронов обеспечивается кулоновскими силами ( F кул = m ое a ц ): В соответствии с моделью Резерфорда, радиус орбиты электрона r и его скорость v могут принимать непрерывный ряд значений ( r < 10 -10 м; v > 1,6. 10 6 м/с).
Слайд 8: Планетарная модель атома Резерфорда содержит два существенных противоречия :
1-е противоречие – поскольку радиус орбиты электрона r и его скорость v в модели Резерфорда могут принимать непрерывный ряд значений, то и энергия электронов в атоме должна была бы иметь непрерывный спектр, а значит, спектр излучения атомов должен был бы быть сплошным. 2-е противоречие – поскольку э лектрон в атоме, в соответствии с моделью Резерфорда, имеет центростремительное ускорение ( 2,6. 10 22 м/с 2 ), то согласно классической электродинамике должен был бы излучать электромагнитные волны, а значит, терять энергию и падать на ядро. На опыте же наблюдаются линейчатые спектры излучения атомов. Понятно, что на опыте это не наблюдается.
Слайд 9: 6.2.2. Линейчатые спектры водородоподобных атомов. Спектральные серии в спектре излучения атомов водорода
Каждому элементу периодической системы соответствует определённый набор спектральных линий, соответствующих набору длин волн излучаемого света. Швейцарский физик И.Бальмер в 1885 году подобрал эмпирическую формулу, описывающую все известные в то время спектральные линии атома водорода в видимой области спектра. В дальнейшем (в начале 20 века) были открыты спектральные серии Вся совокупность спектральных линий разбивается на отдельные группы - серии, в которых расположение линий подчиняется определённым закономерностям. в ультрафиолетовой и инфракрасной областях спектра.
Слайд 10: Обобщённая формула Бальмера, определяющая длину волны излучаемого света:
где m =1,2,3,4,5,6 - номера шести известных в настоящее время серий ; n = m +1, m +2, m +3,...- номера линий каждой из серий; Z - порядковый номер элемента в периодической системе; R =1,097. 10 7 м -1 - постоянная Ридберга. Приведенные формулы подтверждены экспериментально с большой точностью, но теоретического обоснования они долгое время не имели - до тех пор, пока не пришлось отказаться от привычных представлений классической физики. (здесь УФ – ультрафиолетовая область, ИК – инфракрасная область).
Слайд 11: 6.2.3. Дискретность энергетических уровней атомов. Важнейшие представления теории Бора. Правило частот Бора. Стационарные квантовые состояния. Потенциалы возбуждения и ионизации атомов
Первая попытка построить качественно новую – квантовую теорию планетарной модели атома была предпринята в 1913 году датским физиком Нильсом Бором (Нобелевская премия 1922 года). Основная цель Бора состояла в том, чтобы связать в единое целое эмпирические закономерности линейчатых спектров, ядерную модель атома Резерфорда и квантовый характер излучения и поглощения света. В основу теории Бор положил два постулата.
Слайд 12: Первый постулат (постулат стационарных состояний)
Существуют стационарные состояния атома, в которых он не излучает энергию. Стационарным состояниям соответствуют стационарные орбиты электронов, двигаясь по которым, они не излучают энергию. В стационарном состоянии электрон имеет квантованные значения момента импульса : где n =1,2,3,... - номер орбиты, =1,05. 10 -34 Дж. с - постоянная Планка m oe - масса электрона, r n - радиус n -ой орбиты, v n - скорость электрона на n -ой орбите.
Слайд 13: Второй постулат (правило частот Бора)
При переходе атома из одного стационарного состояния в другое (а значит, при переходе электрона с одной стационарной орбиты на другую) испускается или поглощается один фотон с энергией, равной разности энергий соответствующих стационарных состояний: Если W n > W m, энергия излучается. Если W n < W m, энергия поглощается. W=h n=1 n=2 n=3 где и - линейная и циклическая частоты фотона соответственно. W n - W m = h = .
Слайд 14
Совместное решение динамического уравнения и уравнения, выражающего 1-ый постулат Бора позволяет получить формулы для : В модели Бора электрон движется вокруг ядра по круговой стационарной орбите. Центростремительное ускорение создаёт кулоновская сила, действующая со стороны ядра (заряд ядра + Ze ). - периодов обращения электрона на каждой из этих орбит: - скоростей: - радиусов боровских орбит электрона:
Слайд 15
Число n в формулах определяет номер энергетического уровня и называется главным квантовым числом. Полная энергия W n электрона на n -ой орбите в водородоподобном атоме складывается из его кинетической W n кин и потенциальной W n пот энергий: Полная энергия электрона отрицательна, так как внутри атома он находится в связанном состоянии.
Слайд 16
С увеличением номера уровня n энергия водородоподобного атома возрастает ( модуль её уменьшается ), и энергетические уровни сближаются. При n энергия атома W 0. Энергетическое состояние с n =1 называется основным состоянием, а соответствующий энергетический уровень - основным уровнем. Энергетические состояния с n >1 называются возбуждёнными, а соответствующий энергетический уровень - возбуждённым уровнем. В основном состоянии ( n = 1) атом водорода обладает минимальной энергией, равной W 1 = -13,55 эВ. W n, эВ n При переходе электрона с одного энергетического уровня на другой излучается или поглощается фотон, частота которого определяется формулой:
Слайд 17
где с = 3. 10 8 м/с - скорость света в вакууме. Формула для частоты позволяет получить обобщённую формулу Бальмера : . Рассчитанное по этой формуле значение постоянной Ридберга полностью соответствует экспериментальному : Таким образом, согласно теории Бора спектральные линии соответствуют излучению, возникающему в результате перехода атома из возбуждённого состояния, имеющего большую энергию, в состояние с меньшей энергией. Каждой спектральной серии соответствуют переходы на определённый энергетический уровень.
Слайд 18
Энергия, необходимая для удаления электрона из атома, называется энергией ионизации атома и численно равна энергии основного состояния W ион = - W 1. Наименьшая разность потенциалов, которую должен пройти электрон в ускоряющем электрическом поле, чтобы ионизировать невозбуждённый атом электронным ударом, называется потенциалом ионизации : Энергия, необходимая для перехода электрона с низшего энергетического состояния m в высшее n, называется энергией возбуждения атома W возб = W n - W m. Наименьшая разность потенциалов, которую должен пройти электрон в ускоряющем электрическом поле, для возбуждения атома электронным ударом, называется потенциалом возбуждения :
Слайд 19
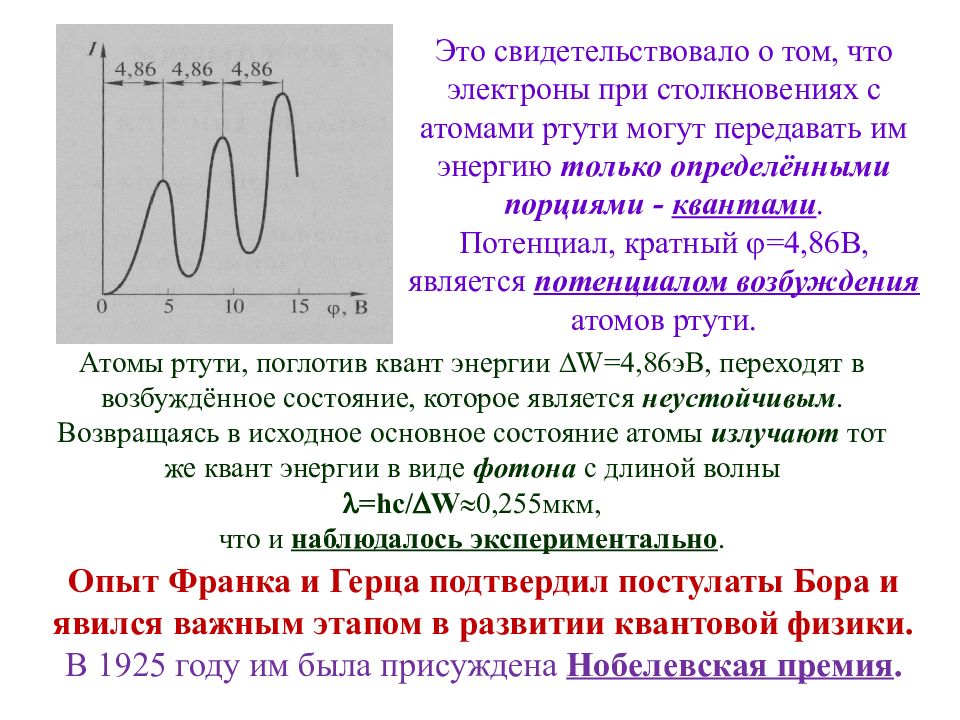
подтвердили опыты, осуществлённые в 1914 году немецкими физиками Джеймсом Франком и Густавом Герцем. 6.2.4. Экспериментальное обоснование идеи квантования (дискретности) состояний атома (опыт Франка и Герца).. Существование дискретных энергетических уровней атома Пропуская электрический ток через вакуумную трубку, наполненную парами ртути при низком давлении ( 13 Па), они обнаружили на анодно-сеточной характеристике ряд равноотстоящих друг от друга пиков:
Слайд 20
Опыт Франка и Герца подтвердил постулаты Бора и явился важным этапом в развитии квантовой физики. В 1925 году им была присуждена Нобелевская премия. Это свидетельствовало о том, что электроны при столкновениях с атомами ртути могут передавать им энергию только определёнными порциями - квантами. Потенциал, кратный =4,86В, является потенциалом возбуждения атомов ртути. Атомы ртути, поглотив квант энергии W =4,86эВ, переходят в возбуждённое состояние, которое является неустойчивым. Возвращаясь в исходное основное состояние атомы излучают тот же квант энергии в виде фотона с длиной волны = hc / W 0,255мкм, что и наблюдалось экспериментально.
Слайд 21: 6.2.5. Принцип соответствия. Затруднения теории Бора
Квантовая физика строилась по новому принципу - она не отвергала классическую физику, а лишь устанавливала пределы её применения и делала новые открытия за этими пределами. Такой подход был чётко сформулирован Нильсом Бором в 1923 году в принципе соответствия : любая новая теория, претендующая на более глубокое описание физической реальности и на более широкую применимость, чем старая, должна включать последнюю как предельный случай. Теория Бора представляла собой переходный этап от классической физики к квантовой (волновой) механике. Принцип соответствия имеет общефизический и философский характер. 6.2.5. Принцип соответствия. Затруднения теории Бора. Теория Бора объяснила спектры излучения водородоподобных систем, но не могла объяснить : 1)интенсивность спектральных линий, 2)причину тех или иных квантовых переходов атомов, 3)особенности спектра излучения атомов гелия.
Важнейший вывод де Бройля – корпускулярно-волновой дуализм универсален, присущ любым видам материи - и полю, и веществу. любые микрочастицы вещества, наряду с корпускулярными свойствами, обладают также и волновыми. 6.3. КВАНТОВАЯ МЕХАНИКА И КОРПУСКУЛЯРНО-ВОЛНОВОЙ ДУАЛИЗМ МАТЕРИИ Любой частице, обладающей импульсом, сопоставляется волновой процесс с длиной волны, 6.3.1. Гипотеза де Бройля. Экспериментальное подтверждение волновых свойств частиц вещества. Дифракция электронов (опыты Дэвиссона и Джермера, Томсона и Тартаковского, Бибермана, Сушкина и Фабриканта). Дифракция нейтронов, атомов и молекул. Электронография, нейтронография. Понятие об электронной оптике. В 1923 году французский физик Луи де Бройль выдвинул гипотезу: определяемой по формуле де Бройля :
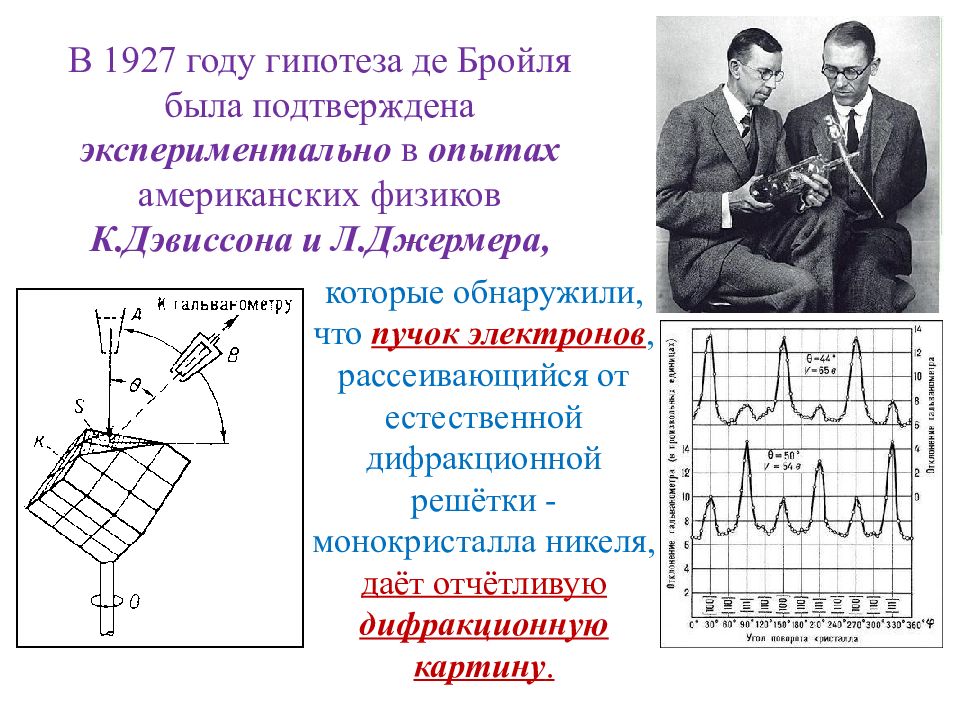
Слайд 23: В 1927 году гипотеза де Бройля была подтверждена экспериментально в опытах американских физиков К.Дэвиссона и Л.Джермера,
к оторые обнаружили, что пучок электронов, рассеивающийся от естественной дифракционной решётки - монокристалла никеля, даёт отчётливую дифракционную картину.
Слайд 24: В 1928 году волновые свойства электронов были обнаружены экспериментально Дж.П.Томсоном (Абердинский университет, Шотландия) и П.С.Тартаковским (Ленинградский университет)
На фотопластинке отчетливо наблюдались концентрические светлые и темные кольца, радиусы которых изменялись с изменением скорости электронов (то есть длины волны) согласно де Бройлю. Полученная дифракционная картина была подобна рентгенограммам, то есть электронная дифракция оказалась подобной рентгеновской дифракции. Они наблюдали дифракцию электронного пучка (энергия электронов ~50кэВ) при прохождении его через тонкие (0,1 1,0мкм) плёнки меди, золота и никеля, имеющие поликристаллическую структуру.
Слайд 25: В 1949 году советские физики Л.М.Биберман, Н.Г.Сушкин и В.А. Фабрикант осуществили дифракцию электронных пучков очень малой интенсивности (время прохождения отдельного электрона через фольгу было в 30000 раз меньше промежутка времени между двумя последовательными попаданиями электронов на фольгу)
Оказалось, что характер дифракционной картины не зависит от интенсивности электронного пучка. Это свидетельствует о том, что волновые свойства присущи каждому электрону в отдельности, а не только их большому потоку. Дифракционные явления наблюдаются не только у электронных, но и у нейтронных, протонных, атомных и молекулярных пучков. Открытие волновых свойств микрочастиц привело к появлению и развитию новых методов исследования структуры веществ - электронографии и нейтронографии, а также к возникновению новой отрасли науки - электронной оптики.
Слайд 26: 6.3.2. Соотношения неопределённостей Гейзенберга. Соотношения неопределённостей как проявление корпускулярно-волнового дуализма частиц. Наборы одновременно измеряемых величин. Философский анализ соотношений неопределённостей и ограниченность механического детерминизма
Немецкий физик В.Гейзенберг, анализируя возможность одновременного измерения координат и импульса микрочастицы, пришёл к выводу, что условия, благоприятные для измерения координат, затрудняют измерение импульса, и наоборот. То есть, координаты и импульс являются дополнительными друг другу и для них выполняются соотношения: или Эти неравенства - соотношения неопределённостей Гейзенберга для координат и импульса микрочастицы.
Слайд 27: В природе объективно не существует состояний микрочастиц с точно определёнными значениями дополнительных друг к другу величин
Практически одновременно с Гейзенбергом Нильс Бор получил соотношение неопределённостей для энергии микрочастицы и времени её взаимодействия с измерительным прибором ( соотношение неопределённостей Бора ) : Соотношения неопределённостей - частный случай и конкретное выражение общего принципа дополнительности, сформулированного Бором в 1927 году - получение экспериментальной информации об одних физических величинах, описывающих микрообъект, неизбежно связано с потерей информации о некоторых других величинах, дополнительных к первым. Главное открытие квантовой механики – вероятностный характер законов микромира.
Слайд 28: 6.4.1. Задание состояния микрочастиц. Волновая функция и её статистический смысл. Амплитуда вероятностей. Суперпозиция состояний в квантовой теории. Объяснение поведения микрочастиц в двущелевом интерферометре. Вероятность в квантовой теории. Диалектика случайного и необходимого в физике. Принцип причинности в квантовой механике
Согласно гипотезе де Бройля микрочастицу можно представлять как волну, а состояние описывать волновой функцией координат и времени – -функцией. Интерпретацию волновой функции дал в 1926 году немецкий физик Макс Борн – квадрат модуля волновой функции определяет вероятность нахождения микрочастицы в единице объёма в окрестности точки с координатами х, у, z в момент времени t. 6.4. КВАНТОВОЕ СОСТОЯНИЕ Основной задачей квантовой механики является нахождение вида волновой функции (х,у, z, t ) и связанных с нею физических следствий в разных условиях.
Слайд 29: Таким образом, согласно М.Борну квадрат модуля волновой функции представляет собой плотность вероятности состояния микрочастицы:
Физический смысл имеет не сама волновая функция, а квадрат её модуля, которым задаётся интенсивность волн де Бройля. Сама же волновая функция играет роль амплитуды вероятности. Волновая функция должна удовлетворять ряду ограничительных условий ( условий регулярности ) – конечность, однозначность, непрерывность. Вероятность нахождения микрочастицы в момент времени t в объёме V : Волновая функция должна быть нормированной - Принцип суперпозиции позволяет объяснить интерференцию микрочастиц. -функция удовлетворяет принципу суперпозиции : где с n ( n = 1,2,3,...) - произвольные, в общем случае комплексные, числа.
Слайд 30: В применении к микрочастицам понятие определённой точки местонахождения и траектории не имеет смысла. Поведение отдельной микрочастицы имеет случайный (вероятностный) характер
В квантовой механике, зная начальное состояние 0 ( причину события) и решая уравнение Шрёдингера, определяют следствие - состояние в последующий момент. Однако никакого нарушения принципа причинности нет, поскольку в квантовой механике понятие состояния микрообъекта приобретает совершенно иной смысл, чем в классической механике. Из соотношений неопределённостей некоторые учёные сделали ошибочный вывод о нарушении принципа причинности в микромире. Состояние системы микрочастиц, определенное в квантовой механике, однозначно вытекает из предшествующего состояния, как того требует принцип причинности. Однако объединение большого числа случайных событий приводит как необходимость к проявлению квантовых закономерностей.
Слайд 31: 6.4.2. Временное уравнение Шрёдингера. Стационарные состояния. Уравнение Шрёдингера для стационарных состояний. Естественные условия
Для решения основной задачи квантовой механики - определения волновой функции микрочастицы, необходимо знать и решить уравнение её движения, то есть волновое уравнение. Основное уравнение нерелятивистской квантовой механики ( v << c ) было записано впервые в 1926 году австрийским физиком Э.Шрёдингером. Это уравнение не выводится, а постулируется. Его справедливость подтверждается его согласием с опытом получаемых с его помощью результатов.
Слайд 32: Уравнение (6) является общим или временным уравнение Шрёдингера
Это уравнение может иметь решение, если выполняются такие условия: 1) волновая функция должна быть конечной, однозначной, непрерывной ; 2) производные / х, / y, / z, / t должны быть непрерывными ; 3) функция | | 2 должна быть интегрируемой (должно выполняться условие нормировки ). функция U = U ( x, y, z ) не зависит от времени и имеет смысл потенциальной энергии, а волновая функция представляется в виде произведения двух функций: ( x, y, z, t )= ( x, y, z ). ( t ) или сокращённо = . . Уравнение Шрёдингера для стационарного поля принимает вид: и решается путём разделения переменных: Здесь W играет роль полной энергии частицы, движущейся в потенциальном поле и обладающей потенциальной энергией U. Для стационарного силового поля
Слайд 33: Нужно отметить, что представление полной энергии частицы W в виде суммы кинетической и потенциальной в квантовой механике имеет ограничения
Координатная часть уравнения Шрёдингера может быть представлена в виде: Решение стационарного уравнения существует лишь при определённом наборе значений энергии, составляющем либо непрерывный, либо дискретный ряд. Эти значения энергии называются собственными. В первом случае частица имеет непрерывный или сплошной энергетический спектр, во втором - дискретный спектр. Решения, которые соответствуют собственным значениям энергии, называются собственными функциями. Таким образом, состояние микрочастицы описывается периодической функцией времени с циклической частотой : и называется стационарным уравнением Шрёдингера. Решение для временной части уравнения Шрёдингера имеет вид: (1)
Слайд 34: 6.4.3. Свободная частица
Для свободной частицы U ( x, y, z ) = 0, а полная её энергия W равна кинетической. Для микрочастицы, движущейся вдоль оси Х со скоростью v x = v, v y = v z = 0, стационарное уравнение Шрёдингера имеет вид: и является дифференциальным уравнением гармонического колебания. С учётом временной части волновой функции полное решение уравнения Шрёдингера для свободной частицы имеет вид: Его решение в экспоненциальной форме имеет вид: Это уравнение плоской монохроматической волны де Бройля, где частота определяется уравнением (1), а волновое число - уравнением (2). Энергетический спектр свободной частицы является непрерывным. (2)
Слайд 35: 6.4.4. Частица в одномерной прямоугольной потенциальной яме (квантование энергии и импульса частицы)
частица движется в потенциальном поле вдоль оси Х, причём её потенциальная энергия в области 0 х равна нулю - U =0, а в областях х 0 и х бесконечно велика - U = . Для нахождения волновой функции необходимо при заданных граничных условиях: (0)= ( )=0 Рассматривается задача нахождения волновой функции частицы, находящейся в одномерной бесконечно глубокой прямоугольной потенциальной «яме» - решить стационарное уравнение Шрёдингера : учитывая, что в пределах потенциальной ямы ( 0 х ) потенциальная энергия частицы равна нулю U =0.
Слайд 36
В пределах потенциальной ямы (0 х ) уравнение Шрёдингера имеет вид: или где Это дифференциальное уравнение гармонического колебания. Его решение в тригонометрической форме имеет вид: где 0 и А - константы, значения которых находятся из первого граничного условия (0) = 0 0 = 0 и из условия нормировки волновой функции. Второе граничное условие ( ) = 0 может быть выполнено только при sink = 0 или k = n, где n =1,2,3,... Это соответствует тому, что волновое число k квантуется, то есть принимает ряд дискретных значений k n, а на ширине потенциальной ямы укладывается целое число полуволн де Б ройля :
Слайд 37: Таким образом, полное решение уравнения Шрёдингера имеет вид:
Из этих уравнений следует, что и импульс, и энергия частицы в потенциальной яме квантуются : Квантованные значения энергии называются энергетическими уровнями, а число n, определяющее номер энергетического уровня, называется главным квантовым числом. Из условия нормировки : определяется значение второй константы в уравнении ( х ) : Таким образом, полное решение уравнения Шрёдингера имеет вид:
Слайд 38
Как видно на графике | n ( х )| 2, внутри потенциальной ямы представление о траектории частицы не применимо. Расстояние между соседними энергетическими уровнями равно: Координатные зависимости собственных функций n (х) и плотности Дискретность энергетических уровней заметна для электрона в атоме ( ~10 -10 м) и практически не заметна для электрона в металле ( ~10 -1 м). вероятности | n (х)| 2 обнаружения частицы внутри потенциальной ямы имеют вид Чем больше n, тем быстрее происходит относительное сближение уровней и их дискретность становится всё менее заметной : В этом состоит принцип соответствия Бора - при больших квантовых числах n квантово-механические закономерности переходят в классические.
Слайд 39: 6.4.5. Туннельный эффект. Прохождение частицы над и под барьером. Непротиворечивость туннельного эффекта закону сохранения энергии. Объяснение туннельного эффекта с помощью соотношений неопределённостей
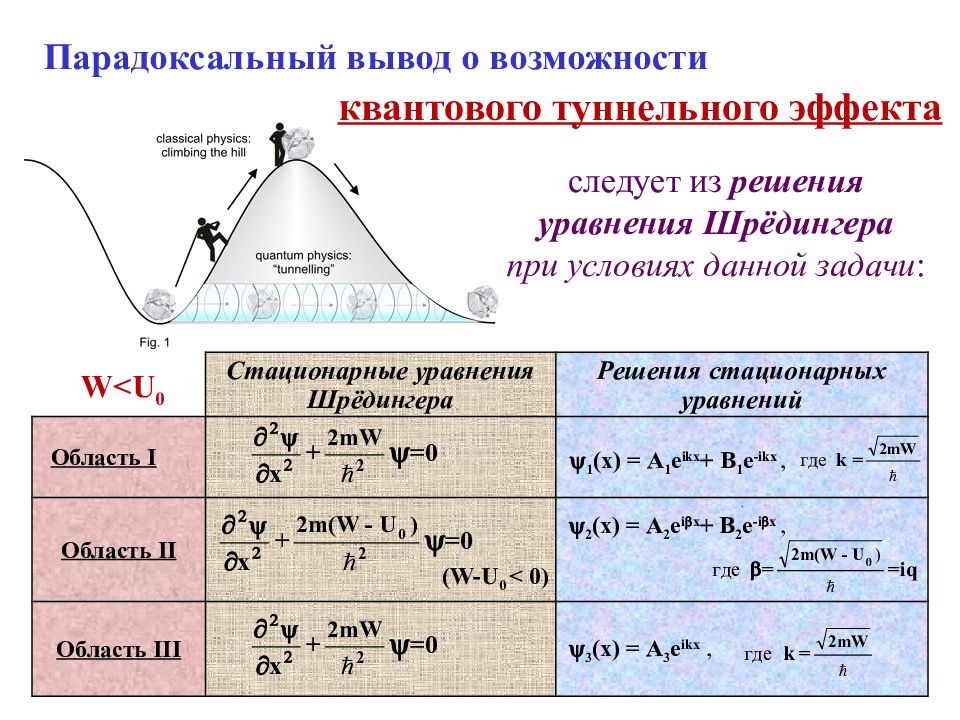
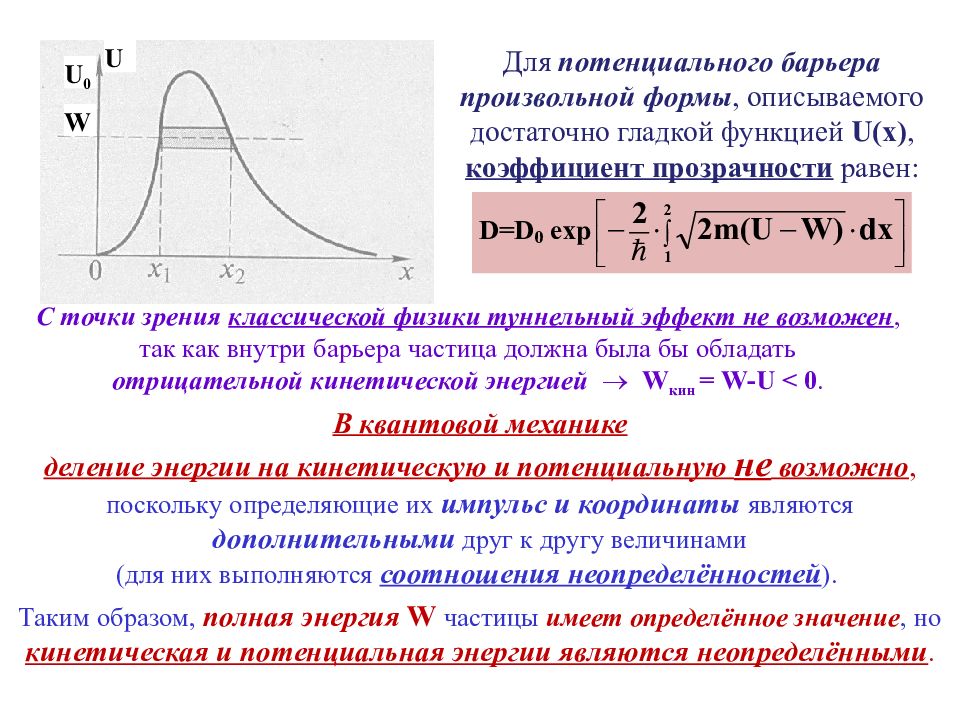
Например, прямоугольный потенциальный барьер : U ( x ) = 0 при х<0 - область I, U ( x ) = U 0 при 0 x - область II, U ( x ) = 0 при х> - область III. Различие в поведении классической и квантовой частиц отчётливо проявляется, когда на пути частицы встречается потенциальный барьер. . Классическая механика Квантовая механика Энергия частицы больше высоты барьера W > U 0 Частица проходит над барьером Существует отличная от нуля вероятность отражения частицы от барьера Энергия частицы меньше высоты барьера W < U 0 Частица отражается от барьера Существует отличная от нуля вероятность прохождения частицы через барьер. Происходит туннелирование. Частица движется с постоянной скоростью вдоль оси Х вблизи прямоугольного потенциального барьера.
Слайд 40: Парадоксальный вывод о возможности
Стационарные уравнения Шрёдингера Решения стационарных уравнений Область I . 1 ( х ) = А 1 е ikx + B 1 е - ikx, Область II ( W - U 0 < 0) . 2 ( х ) = А 2 е i x + B 2 е - i x, Область III 3 ( х ) = А 3 е ikx, Парадоксальный вывод о возможности следует из решения уравнения Шрёдингера при условиях данной задачи : квантового туннельного эффекта W < U 0
Слайд 41: С учётом временных составляющих волновые функции имеют вид:
Область I - волновая функция описывает плоские прямую и отражённую волны де Бройля. Область II - волновая функция содержит экспоненту с действительным показателем и не описывает плоскую волну де Бройля. Область III - волновая функция описывает плоскую прямую волну де Бройля (отражённой волны нет). Область I Область II Область III Таким образом, вероятность нахождения частицы внутри барьера не равна нулю.
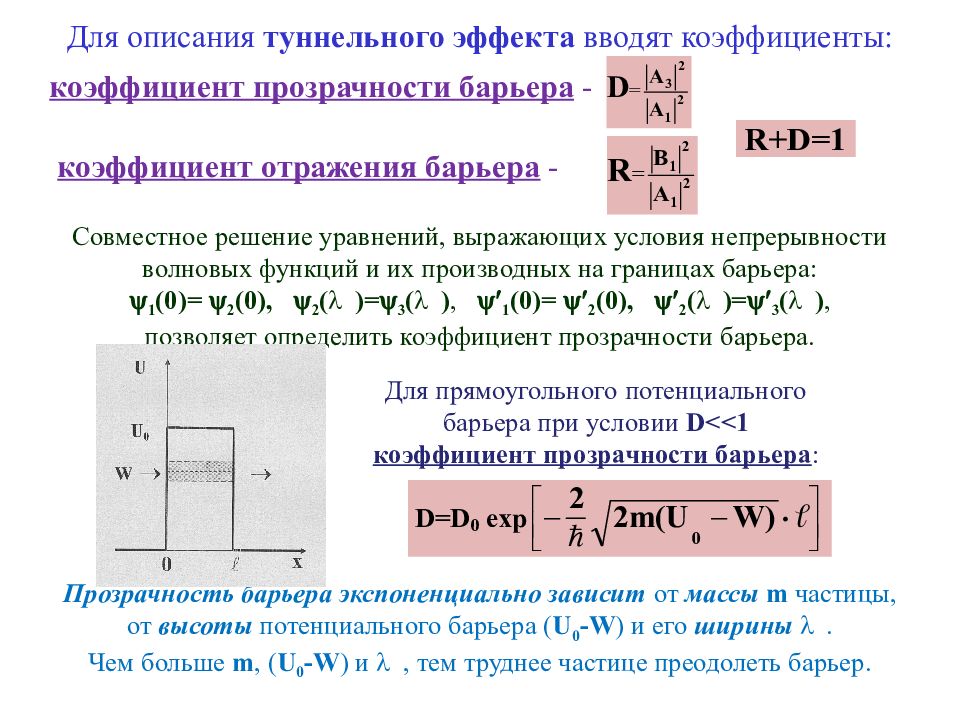
Слайд 42: Для описания туннельного эффекта вводят коэффициенты:
коэффициент прозрачности барьера - коэффициент отражения барьера - Совместное решение уравнений, выражающих условия непрерывности волновых функций и их производных на границах барьера: 1 (0)= 2 (0), 2 ( )= 3 ( ), 1 (0)= 2 (0), 2 ( )= 3 ( ), позволяет определить коэффициент прозрачности барьера. Для прямоугольного потенциального барьера при условии D <<1 коэффициент прозрачности барьера : Прозрачность барьера экспоненциально зависит от массы m частицы, от высоты потенциального барьера ( U 0 - W ) и его ширины . Чем больше m, ( U 0 - W ) и , тем труднее частице преодолеть барьер.
Слайд 43
U 0 U W В квантовой механике деление энергии на кинетическую и потенциальную не возможно, поскольку определяющие их импульс и координаты являются дополнительными друг к другу величинами (для них выполняются соотношения неопределённостей ). С точки зрения классической физики туннельный эффект не возможен, так как внутри барьера частица должна была бы обладать отрицательной кинетической энергией W кин = W - U < 0. Для потенциального барьера произвольной формы, описываемого достаточно гладкой функцией U ( x ), коэффициент прозрачности равен: Таким образом, полная энергия W частицы имеет определённое значение, но кинетическая и потенциальная энергии являются неопределёнными.
Слайд 44
эффект Джозефсона, заключающийся в прохождение сверхпроводящего тока через тонкие диэлектрические прослойки; Основы теории туннельного эффекта были заложены в 1928 году трудами советских физиков Л.И.Мандельштама и М.А Леонтовича. Экспериментальным подтверждением является автоэлектронная эмиссия в металлах, происходящая при напряжённостях полей, в сотни раз меньших по сравнению с классическими оценками. Туннельный эффект лежит в основе многих физических явлений: контактные явления в полупроводниковых туннельных диодах, используемых в генераторах и высокочастотных усилителях; в атомной и ядерной физике: -распад ядер (теория Г.А.Гамова ). туннелирование ядер сквозь кулоновский барьер при термоядерных реакциях;
Слайд 45: 6.4.6. Влияние формы потенциальной ямы на квантование энергии частиц. Гармонический осциллятор. Нулевые колебания
Модель гармонического осциллятора, имеющего параболическую зависимость потенциальной энергии от координаты, широко используется и в классической, и в квантовой физике. Например, она применяется к атомам кристаллической решётки, совершающим тепловые колебания. Свободная частица имеет непрерывный энергетический спектр. В бесконечно глубокой прямоугольной потенциальной яме спектр её становятся квантованным. Возникает вопрос – как влияет форма потенциальной ямы на квантование её энергии ? Например, как квантуется энергия гармонического осциллятора ? С классической точки зрения при Т 0 К тепловые колебания атомов прекращаются, и рассеяние света не должно наблюдаться. Эксперименты по изучению рассеяния света атомами кристаллов при сверхнизких темп ературах показали, что при Т 0 К интенсивность рассеянного света стремится к некоторому предельному, не равному нулю значению.
Слайд 46
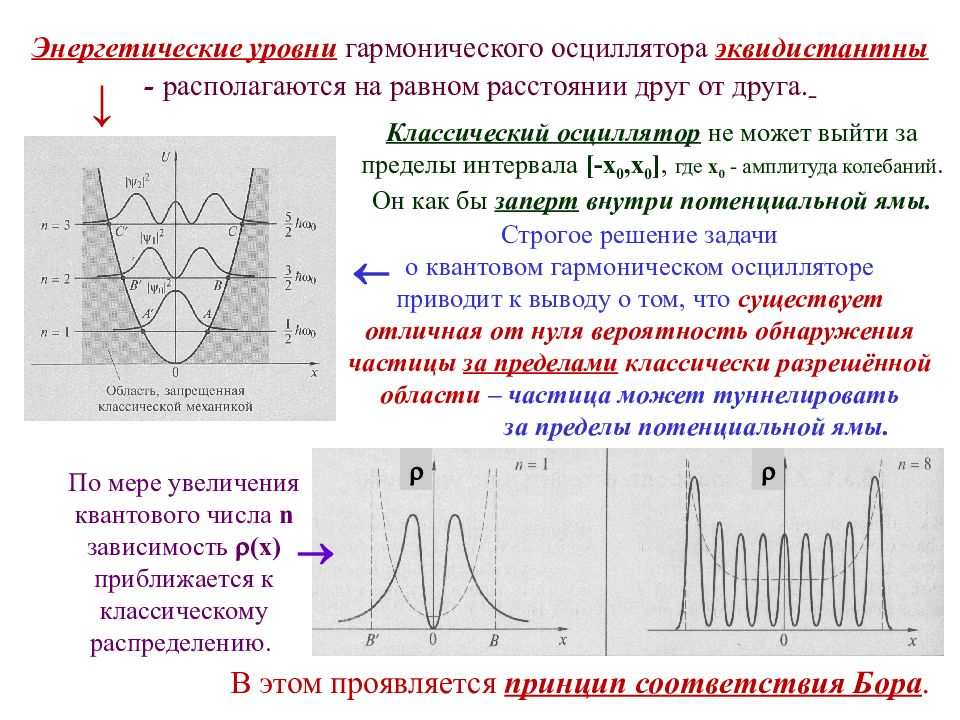
описывается уравнением Шрёдингера Решение уравнения при заданных граничных условиях возможно только при Квантовый гармонический осциллятор квантованных значениях энергии осциллятора: Выводы квантовой теории о существовании нулевых колебаний гармонического осциллятора подтверждают эксперименты по изучению рассеяния света при сверхнизких температурах. Энергетические уровни гармонического осциллятора эквидистантны. В квантовой механике из соотношений неопределённостей следует, что полная энергия квантового гармонического осциллятора и амплитуда его колебаний не могут быть равны нулю. Существует минимальное значение энергии, называемое нулевой энергией гармонического осциллятора :
Слайд 47
По мере увеличения квантового числа n зависимость ( х ) приближается к классическому распределению. Строгое решение задачи о квантовом гармоническом осцилляторе приводит к выводу о том, что существует отличная от нуля вероятность обнаружения частицы за пределами классически разрешённой области – частица может туннелировать за пределы потенциальной ямы. Энергетические уровни гармонического осциллятора эквидистантны - располагаются на равном расстоянии друг от друга. Классический осциллятор не может выйти за пределы интервала [- x 0, x 0 ], где x 0 - амплитуда колебаний. Он как бы заперт внутри потенциальной ямы. В этом проявляется принцип соответствия Бора. ↓