В процессе движения частицы на неё могут действовать два вида сил: консервативные и неконсервативные. В качестве неконсервативных сил могут выступать силы трения , возникающие при скольжении тела по некоторой поверхности и пропорциональные силам, прижимающим тело к поверхности. Коэффициент пропорциональности называется коэффициентом трения. Работа этих сил не может быть равной нулю по замкнутой траекториии всегда отрицательна.
Слайд 3: Работа консервативных и неконсервативных сил
Кроме того, неконсервативными силами являются также т.н. силы тяги, превращающие немеханические виды энергии в механические. Их работа на замкнутом контуре также не равна в общем случае нулю. С использованием разделения сил на консервативные и неконсервативные закон изменения кинетической энергии можно записать в следующем виде .
Слайд 4: З.И.К.Э. с использованием потенциальной энергии
Первое слагаемое справа от равенства представляет собой работу консервативных сил, а второе – неконсервативных сил. Работу консервативных сил можно представить, как убыль потенциальной энергии, тогда З.И.К.Э. запишется так:
Слайд 5: Полная энергия
Перенесём первое слагаемое справа в левую часть и объединим его с правым членом. Выражение, стоящее в скобках, называется полной механической энергией материальной точки и обозначается E. Определение.Сумма кинетической и потенциальной энергии называется полной энергией.
Слайд 6: Закон изменения полной энергии материальной точки
С учётом полной энергии закон изменения кинетической энергии запишется так: . Это утверждение носит название закона изменения полной энергии материальной точки. Оно гласит: «Изменение полной энергии материальной точки за некоторый промежуток времени равно работе всех неконсервативных сил, действующих на материальную точку». Таким образом, изменить полную энергию материальной точки могут только неконсервативные силы.
Слайд 7: ЗИПЭ с учётом сил трения и тяги
Если имеются как силы рения, так и силы тяги, то ЗИПЭ будет выглядеть так: Поскольку работа сил трения всегда отрицательна, а работа сил тяги может быть как положительной, так и отрицательной, то полная энергия может как убывать, так и возрастать.
Слайд 8: Следствия из закона И.П.Э
1. 2. 3. Это ЗСПЭ: если работа всех неконсервативных сил равна нулю, то полная энергия не меняется.
Слайд 9: Замечания
1. Если полная энергия меняется, то это не означает, что она исчезает в никуда или берётся ни откуда. Просто происходить превращение механической энергии в другие виды (в частности а тело) и обратно. 2. Если полная энергия сохранятся, то это не значит, что не меняется кинетическая и потенциальная энергии по отдельности. Они могут меняться, но так, что полная не меняется.
Слайд 10: 4. Колебания
4.1. Силы упругости. Вторым примером потенциального поля может служить поле упругих сил. Силы упругости прямо пропорционально зависят от смещения . Коэффициент пропорциональности называется коэффициентом упругости, а сам закон носит название закона Гука.
Слайд 11: Работа сил упругости
Найдём работу силы упругости . Подставим силу упругости и проинтегрируем
Слайд 12: Потенциальная энергия упругих сил
Отсюда видно, что работа зависит лишь от начального и конечного состояний, поэтому поле сил упругости является потенциальным. Его работу можно представить, как убыль потенциальной энергии . Сравнивая это с работой упругих сил, находим: .
Слайд 13: 4.2. Уравнение упругих колебаний
Пусть на материальную точку действует сила упругости. Такая материальная точка называется пружинным маятником. Согласно закону Ньютона , заменив ускорение второй производной от координаты по времени, получим уравнение , которое называется уравнением упругих колебаний, т.к. ему удовлетворяет функция гармонических колебаний :
Слайд 15: Гармонические колебания
Чтобы это доказать, что уравнение гармонических колебаний удовлетворяет уравнению упругих колебаний, найдем вторую производную от функции и подставим её в уравнение движения пружинного маятника Подставим это в формулу закона движения пружинного маятника, получим
Слайд 16: Частота упругих колебаний
Из этого равенства видно, что уравнение действительно удовлетворяется, если выполняется условие, откуда находим частоту упругих колебаний: . Так определяется частота упругих колебаний. Она прямо зависит от коэффициента упругости и обратно от массы материальной точки.
Слайд 18: Затухающие колебания. progr
Если на маятник действует сила трения, его энергия колебания уменьшается. Вместе с этим уменьшается амплитуда по закону: Progr D: Progr E: Progr F: Progr G : – коэффициент затухания.
Слайд 19: 4. 3. Вынужденные колебания
Допустим, что кроме упругой силы на материальную точку действует ещё одна сила, меняющаяся по гармоническому закону. . Тогда уравнение второго закона Ньютона будет выглядеть следующим образом ,
Слайд 20: Обозначения
Разделим уравнение на массу тела и введём обозначения. Величина носит название собственной частоты в отличие от частоты колебания вынуждающей силы. Это величина вынуждающей силы, действующая на единицу массы материальной точки.
Слайд 21: Уравнение вынужденных колебаний
В новых обозначениях уравнение вынужденных колебаний будет иметь вид: Это равенство называется уравнением вынужденных колебаний.
Слайд 22: Решение уравнения вынужденных колебаний
Ищем решение этого уравнения в виде . Подставим производную второго порядка в уравнение вынужденных колебаний . Это уравнение позволяет найти амплитуду вынужденных колебаний .
Слайд 24: Немонотонность зависимости амплитуды
Как видно из этого равенства, амплитуда вынужденных колебаний зависит от частоты. Характерным в этой зависимости является немонотонность. Если частота вынуждающей силы далека от собственной частоты колебания маятника, его амплитуда мала. По мере приближения частоты вынуждающей силы к собственной амплитуда нарастает.
Слайд 25: Амплитуда вынужденных колебаний при наличии трения
Если на маятник кроме сил у пругости и вынуждающей силы действует ещё сила трения, она вызывает затухание, характеризующееся коэффициентом затухания. В этом случае амплитуда вынужденных колебаний рассчитывается по формуле:
Слайд 26: Резонанс
Когда частоты равны амплитуда неограниченно возрастает. Это явление называется резонансом. На практике амплитуда в резонансе не возрастает до бесконечности, потому что препятствует сила трения, которую мы в нашем случае не учитывали.
Слайд 28: 4.4. Волны. Понятие волны, типы волн
Если частицы некоторой материальной среды упруго связаны, среде называется упругой средой. Колебание одной из частиц упругой среды приводит к возникновению колебаний по всей среде. Колебания как бы распространяются от одной частицы к другой.
Слайд 29: Типы волн
Определение. Явление распространения колебаний в упругой среде называется волной. Частица, с которой начинается колебание, называется источником волн. Волны, колебания частиц среды в которой параллельны направлению распространения волны, называются продольными. Волны, колебания частиц в которых перпендикулярны направлению распространения волны, называются поперечными волнами.
Слайд 31: Волновая функция
Обозначим смещение частиц упругой среды от положения равновесия через. Поскольку разные частицы отклонены по-разному, их смещение зависит от координат. Поскольку частицы колеблются, их смещение зависит от времени. Так что в общем случае смещение частиц среды есть функция двух переменных: . Эта функция носит название волновой функции.
Слайд 32: Запаздывание волны
Пусть источник волн колеблется по закону: Тогда до точки, находящейся на расстоянии от источника волн волна дойдёт через промежуток времени, равный: Где скорость распространения волны.
Слайд 33: Уравнение волны
Тогда закон колебания этой точки будет иметь вид: Это и есть уравнение плоской волны. Если волна распространяется вдоль оси, то уравнение волны принимает вид:
Слайд 34: Длина волны
Определение. Длиной волны называется наименьшее расстояние в пространстве вдоль направления распространения волны, которое волна проходит за один период, Из этой формулы следуют другие формулы:
Слайд 35: Уравнение волны с помощью понятия длины волны
С помощью длины волны уравнение волны можно записать так: называется волновым числом. С его помощью
Слайд 36: 4.5. Интенсивность волн
Поскольку волна представляет собой колебания частиц, она обладает, как потенциальной, так и кинетической энергией, а, значит, и полной энергией. Эта энергия переносится волной, что создаёт поток энергии. Определение. Потоком энергии называется величина, равная энергии, переносимой волной через некоторую площадку за единицу времени. . Так что.
Слайд 37: Плотность потока
Плотностью потока энергии называется величина, равная потоку через единицу площадки, перпендикулярной распространения волны: Размерность
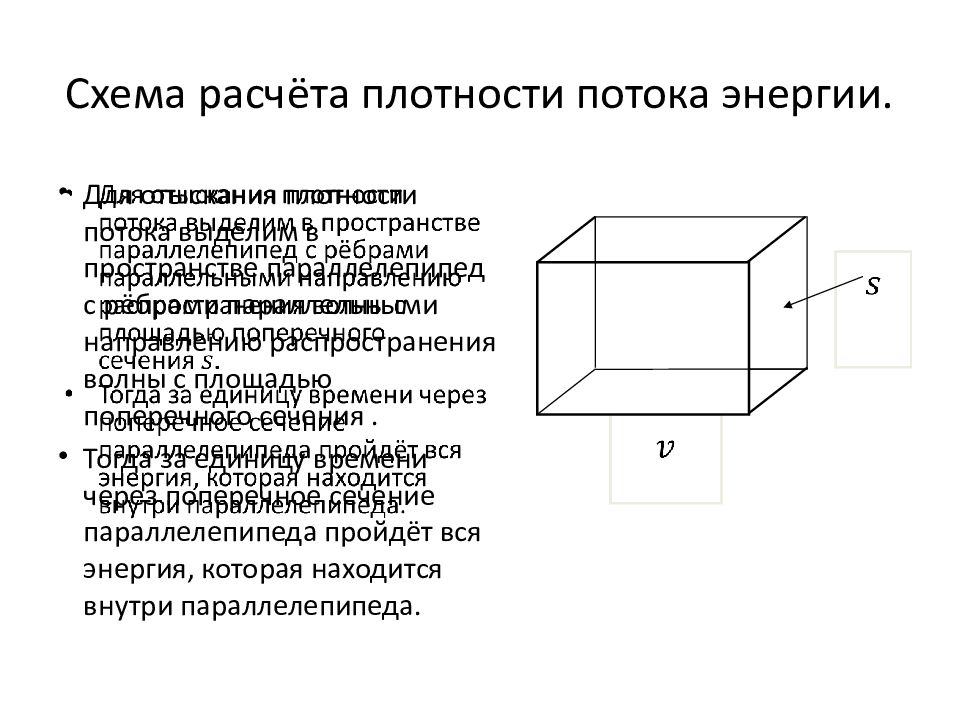
Слайд 38: Схема расчёта плотности потока энергии
Для отыскания плотности потока выделим в пространстве параллелепипед с рёбрами параллельными направлению распространения волны с площадью поперечного сечения. Тогда за единицу времени через поперечное сечение параллелепипеда пройдёт вся эн е ргия, которая находится внутри параллелепипеда.
Слайд 39: Формула вектора Умова
То есть – плотность энергии. Отсюда можно найти плотность потока энергии: Или в векторном виде: В этом виде плотность потока энергии называется вектором Умова.
Слайд 40: 4.6. Интерференция волн, стоячие волны
Интенсивностью волн называется среднее за достаточно большой промежуток времени значение плотности потока энергии волны. Если в некоторой точке пространства встречаются две волны, частицы в этой точке участвуют в двух колебаниях. Если частота волн разная, волны называются некогерентными, а результирующая интенсивность будет просто равна сумме интенсивностей складываемых волн.
Слайд 41: Разность фаз
Если частоты волн одинаковые, волны называются когерентными. В этом случае они могут усиливать друг друга, а могут ослаблять. Это зависит от разности фаз колебаний, приходящих от разных волн. Если разность фаз рана чётному числу, волны усиливают друг друга, если разность фаз равна нечётному числу, волны ослабляют друг друга.
Слайд 42: Разность хода волн
Разность фаз в свою очередь зависит от так называемой разности хода волн, т.е. от разности расстояний, которые прошли волны до встречи. Если эта разность равно чётному числу длин полуволн, разность фаз равна чётному числу, и волны усиливают друг друга. Если разность хода равна нечётному числу длин полуволн, волны ослабляют друг друга.
Слайд 43: Условия максимума и минимума. progr
Таким образом, при наложении двух волн, в некоторых точках пространства волны усиливают друг друга, в других точка ослабляют. Такое взаимодействие волн называется интерференцией. Условие максимума: Условие минимума: Progr D: Progr E: Progr F: Progr G:
Слайд 44: Стоячие волны. progr
Частным случаем интерференции являются стоячие волны. Они характерны тем, что все частицы в них колеблются в одной фазе, но с разными амплитудами: Progr D: Progr E: Progr F: Progr G:
Слайд 45: Узлы и пучности
Точки стоячей волны, в которых наблюдается максимум амплитуды, называются пучностями, эти точки соответствуют координатам. Точки, в которых наблюдаются нулевые амплитуды, называются узлами. Они соответствуют координатам
Слайд 46: 4.7. Эффект Доплера
Когда автомобиль приближается, а затем, пройдя мимо, начинает удаляться, высота звука его двигателя резко понижается. Это значит, что частота, которую принимает источник, зависит не только от того, какую частоту испускает источник, но и от того как он движется. Если источник звука приближается, частота волны, воспринимаемая приёмником, больше, чем частота волны, излучаемой источником.
Слайд 47: Определение эффекта Доплера
Опыт также показывает, что частота волны, воспринимаемой приёмником, зависит также и от движения приёмника. Определение. Явление зависимости частоты волны, воспринимаемой приёмником от скорости движения приёмника и источника волн, называется эффектом Доплера.
Слайд 48: Длина волны в неподвижной системе
Пусть источник волн испускает волну с частотой. Скорость распространения волны в данной среде обозначим. Если источник покоится относительно среды, то длина волны, которую он испускает, будет равна :
Слайд 49: Длина волны в подвижной системе
Если же источник движется в сторону испускания волны, то длина волны уменьшится из-за того, что за время одного периода источник сместится на расстояние Именно на такую величину уменьшится длина волны, т.е.
Слайд 50: Соотношение между частотами
Имея в виду: для частоты получим соотношение: Выразим отсюда новую частоту:
Слайд 51: Удаление источника
Если же источник удаляется, т.е. движется в сторону, противоположную испусканию волны, то длина волны, наоборот, увеличивается, а частота уменьшается, т.е.
Слайд 52: Общая формула
Откуда Таким образом, в общем случае подвижного источника:
Слайд 53: Скорость звука в подвижной системе
Пусть теперь движется приёмник и навстречу волне. Тогда скорость волны относительно приёмника будет больше скорости волны, как раз на скорость приёмника, т.е. А длина волны при этом будет прежней.
Слайд 54: Движение приёмника на встречу волне
Тогда новый период волны можно будет найти по формуле: Совершенно аналогично можно показать, что для удаляющегося приёмника
Слайд 55: Общая формула эффекта Доплера
Так что в общем случае движения приёмника: И, наконец, если движутся оба устройства: