Слайд 2: 1. ВИДЫ ВОЛН
Волнами называется процесс распространения колебаний в пространстве с течением времени. Характерное свойство волн состоит в том, что перенос энергии волной происходит без переноса вещества. Основными видами волн являются механические (упругие ) волны: в частности звуковые и сейсмические волны, волны на поверхности вод ы; и электромагнитные волны: в частности световые волны и радиоволны.
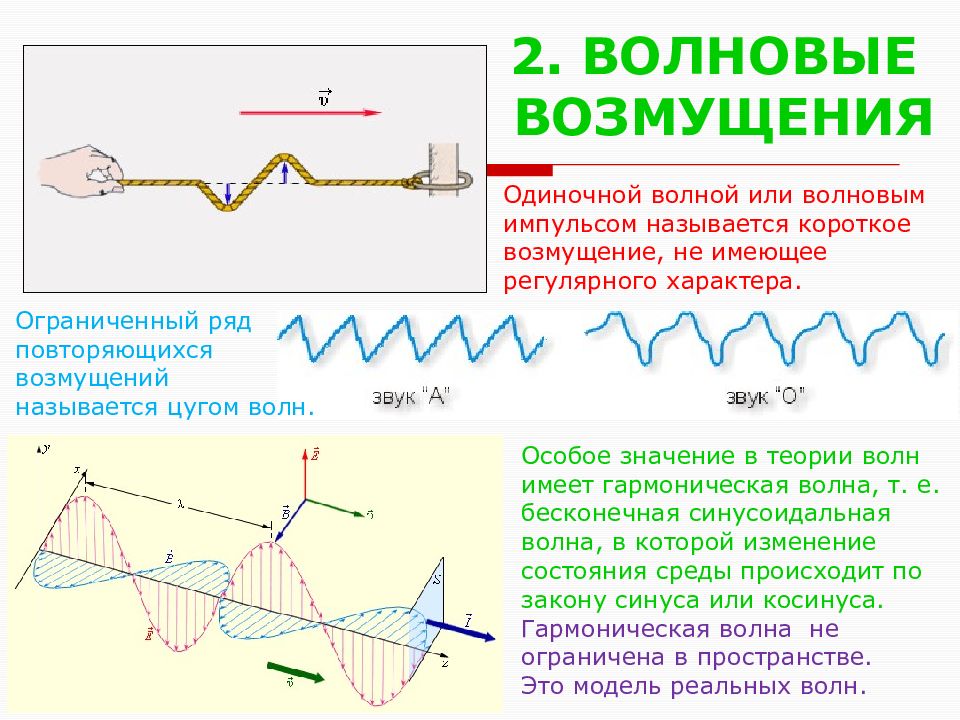
Слайд 3: 2. ВОЛНОВЫЕ ВОЗМУЩЕНИЯ
Одиночной волной или волновым импульсом называется короткое возмущение, не имеющее регулярного характера. Ограниченный ряд повторяющихся возмущений называется цугом волн. Особое значение в теории волн имеет гармоническая волна, т. е. бесконечная синусоидальная волна, в которой изменение состояния среды происходит по закону синуса или косинуса. Гармоническая волна не ограничена в пространстве. Это модель реальных волн.
Слайд 4: 3. ВОЗНИКНОВЕНИЕ ВОЛНЫ
Если в каком-либо месте упругой среды (твердой, жидкой, газообразной) возбудить колебания ее частиц, то вследствие взаимодействия между частицами это колебание будет распространяться в среде от частицы к частице с некоторой скоростью – в среде возникнет волна. Частицы среды, в которой распространяется волна, не вовлекаются в поступательное движение, они лишь совершают колебания около своих положений равновесия.
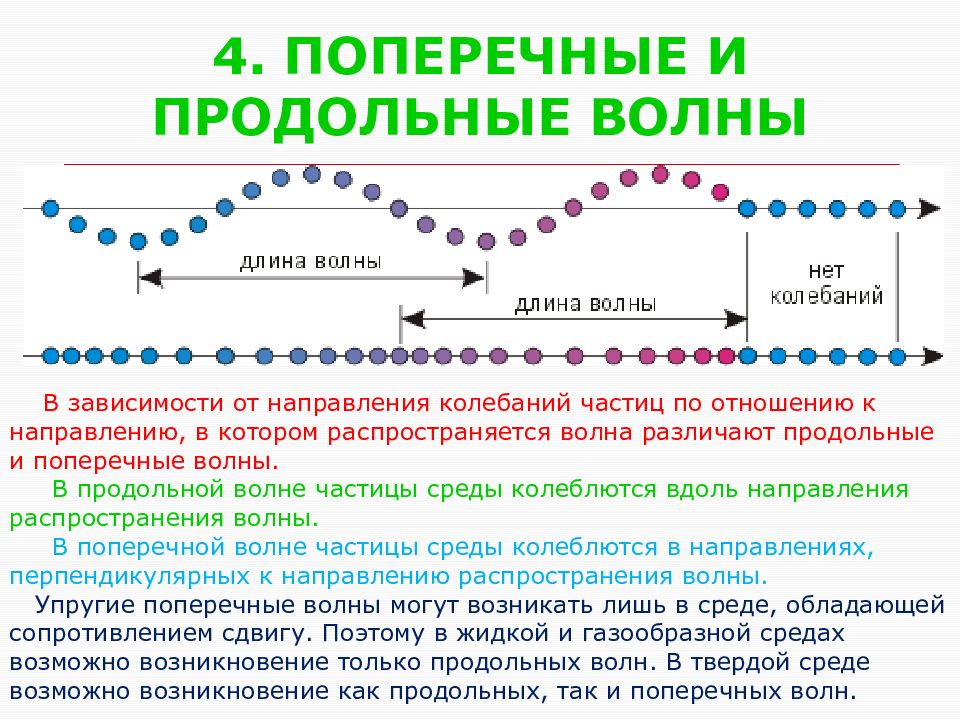
Слайд 5: 4. ПОПЕРЕЧНЫЕ И ПРОДОЛЬНЫЕ ВОЛНЫ
В зависимости от направления колебаний частиц по отношению к направлению, в котором распространяется волна различают продольные и поперечные волны. В продольной волне частицы среды колеблются вдоль направления распространения волны. В поперечной волне частицы среды колеблются в направлениях, перпендикулярных к направлению распространения волны. Упругие поперечные волны могут возникать лишь в среде, обладающей сопротивлением сдвигу. Поэтому в жидкой и газообразной средах возможно возникновение только продольных волн. В твердой среде возможно возникновение как продольных, так и поперечных волн.
Слайд 6: 5. ВОЛНОВОЙ ФРОНТ. ВОЛНОВАЯ ПОВЕРХНОСТЬ
Распространяясь от источника колебаний, волновой процесс охватывает все новые и новые области пространства. Геометрическое место точек, до которых доходят колебания к данному моменту времени, называется фронтом волны или волновым фронтом. Фронт волны отделяет часть пространства, уже вовлеченную в волновой процесс, от области, в которой колебания еще не возникли. Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью. Волновую поверхность можно провести через любую точку пространства, охваченного волновым процессом. Следовательно волновых поверхностей существует бесконечно много.
Слайд 7: 6. ВОЛНЫ ПЛОССКАЯ И СФЕРИЧЕСКАЯ
Волновые поверхности могут быть любой формы. В простейших случаях они имеют форму плоскости (плоская волна) или сферы (сферическая волна). В плоской волне волновые поверхности представляют собой множество параллельных плоскостей, в сферической волне – концентрических сфер.
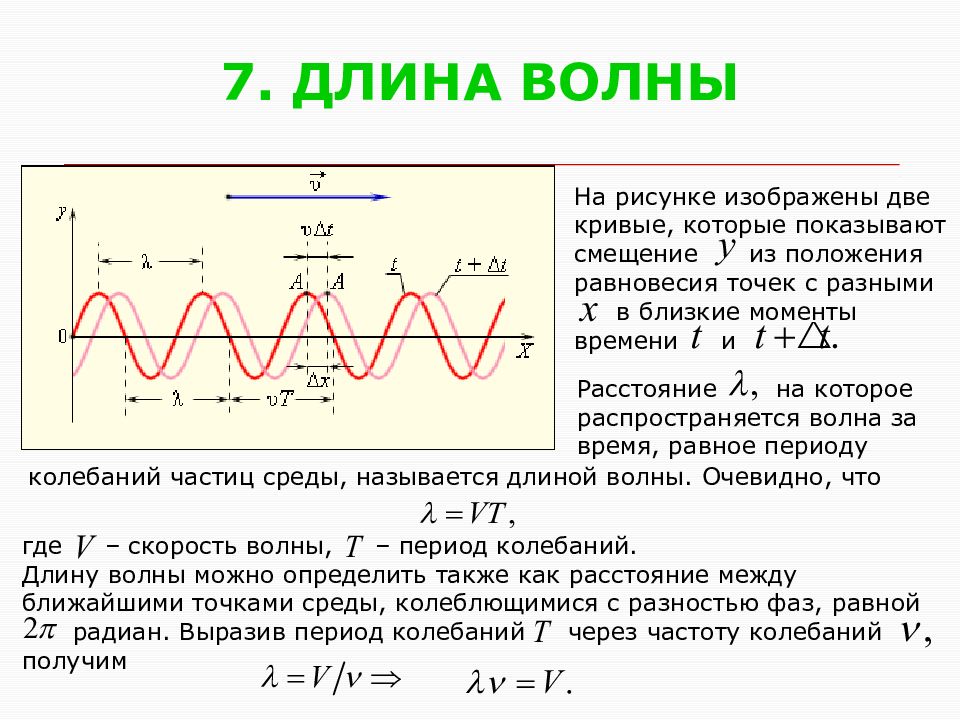
Слайд 8: 7. ДЛИНА ВОЛНЫ
На рисунке изображены две кривые, которые показывают смещение из положения равновесия точек с разными в близкие моменты времени и Расстояние на которое распространяется волна за время, равное периоду колебаний частиц среды, называется длиной волны. Очевидно, что где – скорость волны, – период колебаний. Длину волны можно определить также как расстояние между ближайшими точками среды, колеблющимися с разностью фаз, равной радиан. Выразив период колебаний через частоту колебаний получим
Слайд 10: 9. УРАВНЕНИЕ СФЕРИЧЕСКОЙ ВОЛНЫ
Всякий реальный источник волн обладает некоторой протяженностью. Однако если ограничиться рассмотрением волны на расстояниях от источника значительно превышающих его размеры, то источник можно считать точечным (волновая зона). В изотропной и однородной среде волна, порождаемая точечным источником будет сферической. Допустим, что фаза колебаний источника равна Тогда точки, лежащие на волновой поверхности радиуса будут совершать колебания с запаздыванием по времени на Даже если волна не поглощается средой, ее амплитуда уменьшается с удалением от источника по закону т.к. энергия распределяется по поверхности все большего радиуса. Тогда ( – амплитуда на единичном радиусе ).
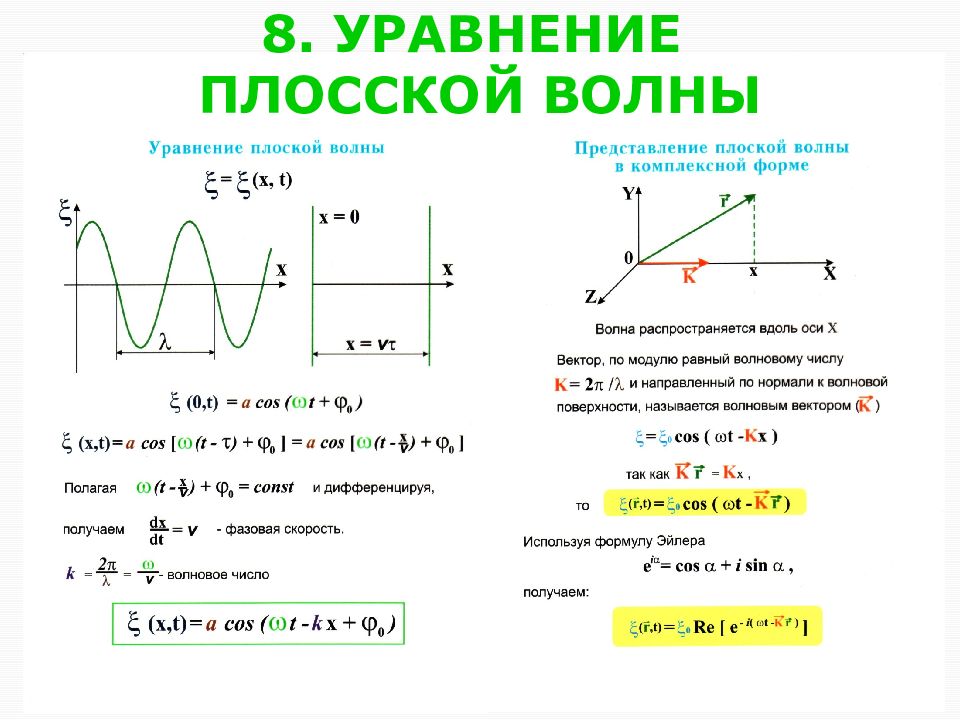
Слайд 11: 10. ВОЛНОВОЕ УРАВНЕНИЕ
Уравнение любой волны является решением дифференциального уравнения, называемого волновым. Чтобы установить вид волнового уравнения, сопоставим вторые частные производные по времени и координатам от уравнения для плоской волны: Сложим производные по координатам
Слайд 12: 11. СКОРОСТЬ УПРУГИХ ВОЛН ( I)
Пусть в направлении оси рас-пространяется продольная плоская волна. Выделим в среде цилиндрический объем с площадью основания и высотой Основание цилиндра с координатой имеет в данный момент времени некоторое смещение а основание с координатой имеет другое смещение Т. е. рассматриваемый объем дефор- мируется – он получает удлинение Величина задает среднюю относительную деформацию цилиндра. Чтобы получить точную относительную деформацию в сечении нужно устремить к нулю. Таким образом,
Слайд 13: 1 2. СКОРОСТЬ УПРУГИХ ВОЛН ( II)
Наличие деформации растяжения- сжатия свидетельствует о существовании нормального напряжения которое по закону Гука пропорционального величине относительной деформации. То есть – модуль Юнга. Там, где отклонения частиц от по- ложения равновесия максимальны, деформация и напряжение равны нулю. В местах, где частицы прохо- дят через положение равновесия, деформация и напряжение дости- гают максимального значения, при- чем положительные (растяжение) и отрицательные (сжатие) деформа- ции чередуются друг с другом.
Слайд 14: 11. СКОРОСТЬ УПРУГИХ ВОЛН ( III)
Напишем уравнение движения для выделенного цилиндрического объема. Полагая, что мы можем считать проекцию ускорения одинаковой для всех точек внутри выделенного цилиндра, то есть – масса выделенного объема. Проекция на ось силы упругости, действующей на цилиндр, равна произведению площади основания цилиндра на разность нормальных напряжений на основаниях цилиндра В результате получаем уравнение движения ( II закон Ньютона) для случая малых деформаций
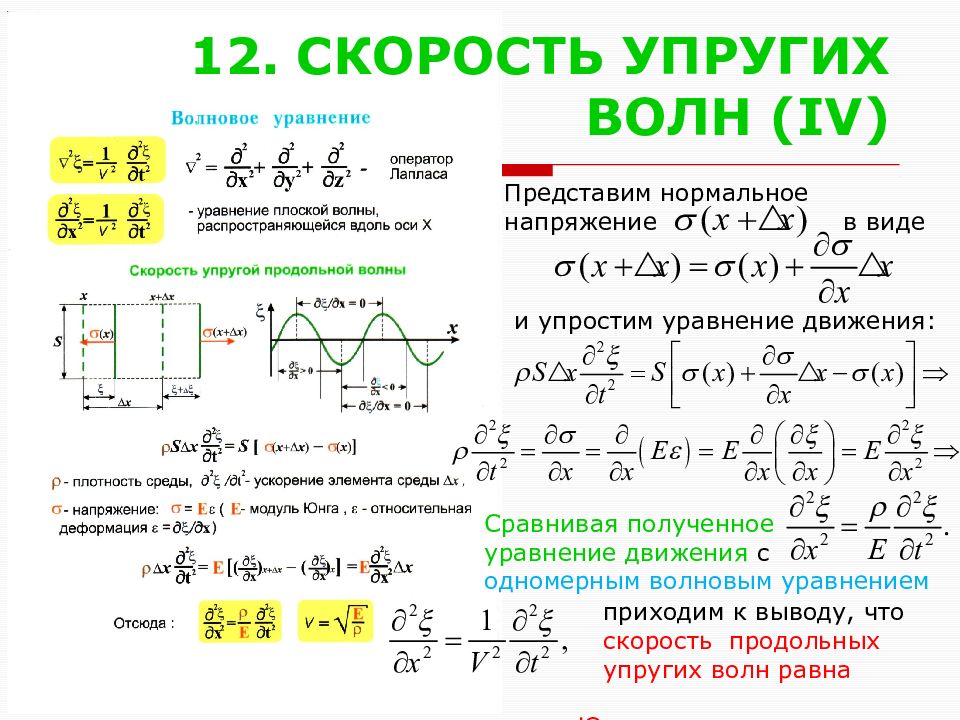
Слайд 15: 1 2. СКОРОСТЬ УПРУГИХ ВОЛН ( IV)
Представим нормальное напряжение в виде и упростим уравнение движения: Сравнивая полученное уравнение движения с одномерным волновым уравнением приходим к выводу, что скорость продольных упругих волн равна корню квадратному из отношения модуля Юнга среды к ее плотности.
Слайд 16: 15. ЭНЕРГИЯ УПРУГОЙ ВОЛНЫ ( I)
Пусть в некоторой среде распространяется вдоль оси плоская продольная волна Выделим в среде элементарный объем настолько малый, чтобы скорость и деформацию во всех точках этого объема можно считать одинаковыми и равными соответственно и Выделенный нами объем обладает кинетической энергией, а также потенциальной энергией упругой деформации: Модуль Юнга среды и фазовая скорость волны связаны по формуле
Слайд 17: 16. ЭНЕРГИЯ УПРУГОЙ ВОЛНЫ (II)
C умма кинетической и потенциальной энергии выделенного объема дает его полную механическую энергию, то есть Дифференцирование уравнения плоской волны по t и по x дает Полученное выражение означает, что объемная плотность энергии волны в каждый момент времени в разных точках пространства различна. В данной точке плотность энергии изменяется со временем по закону квадрата синуса. Этот результат справедлив для всех механических волн.
Слайд 18: 17. ПОТОК ЭНЕРГИИ ВОЛНЫ
Среда, в которой распространяется волна, обладает дополнительным запасом энергии. Эта энергия доставляется от источника колебаний в различные точки среды самой волной; следовательно, волна переносит с собой энергию. Количество энергии, переносимое волной через некоторую поверхность в единицу времени, называется потоком энергии. Если через данную за время переносится энергия то поток энергии равен
Слайд 19: 18. ПЛОТНОСТЬ ПОТОКА ЭНЕРГИИ
Поток энергии в разных точках среды может быть различным. Для характеристики течения энергии в разных точках введена векторная физическая величина – плотность потока энергии. Плотность потока энергии численно равна потоку энергии через единичную площадку, помещенную в данной точке перпендикулярно к направлению, в котором переносится энергия. Направление вектора плотности потока энергии совпадает с направлением переноса энергии. Зная вектор плотности потока энергии во всех точках произвольной поверхности можно вычислить поток энергии через эту поверхность:
Слайд 20: 19. ИНТЕНСИВНОСТЬ ВОЛНЫ
Плотность потока энергии как и объемная плотность энергии различна в разных точках пространства, а в данной точке изменяется со временем по закону квадрата синуса. Среднее значение квадрата синуса за период равно поэтому для среднего по времени значение плотности потока энергии справедливо Эта величина называется интенсивностью волны Таким образом, интенсивность волны в данной точке это среднее по времени значение плотности потока энергии волны в этой точке пространства. Полученные выражения для интенсивности и объемной плотности энергии справедливы для всех механических волн.
Слайд 21: 20. АМПЛИТУДА СФЕРИЧЕСКОЙ ВОЛНЫ
Вычислим среднее по времени значение потока энергии через некоторую волновую поверхность незатухающей сферической волны. В каждой точке сферической волновой поверхности векторы и совпадают по направлению. Кроме того, модуль вектора для всех точек поверхности сферы одинаков ( r = const). Следовательно Если энергия волны не поглощается средой, то среднее значение потока энергии через сферу любого радиуса должно оставаться постоянным, т.е.
Слайд 22: 21. ПРИНЦИП СУПЕРПОЗИЦИИ ВОЛН
Если в среде распространяется одновременно несколько волн, то колебания частиц среды оказываются суммой колебаний, которые совершали бы частицы при распространении каждой из волн в отдельности. Следовательно, волны просто накладываются одна на другую, не возмущая друг друга. Это утверждение называется принципом суперпозиции волн. В случае, когда колебания, обусловленные отдельными волнами, обладают в каждой из точек среды постоянной разностью фаз, волны называются когерентными. При сложении когерентных волн возникает явление интерференции, заключающееся в том, что колебания в одних точках усиливают, а в других ослабевают друг друга.
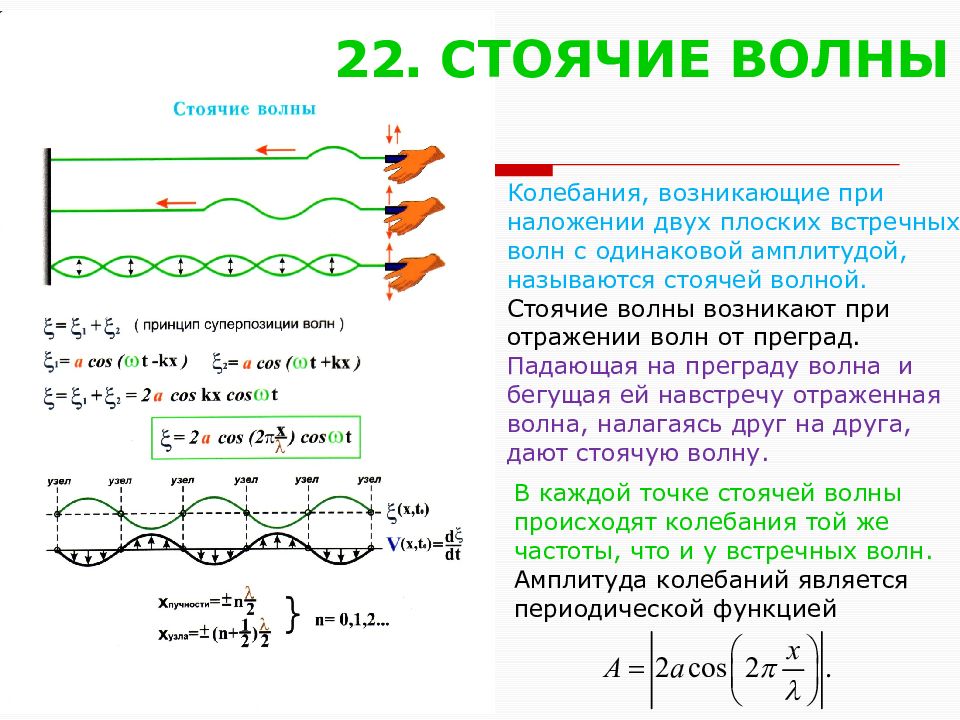
Слайд 23: 22. СТОЯЧИЕ ВОЛНЫ
Колебания, возникающие при наложении двух плоских встречных волн с одинаковой амплитудой, называются стоячей волной. Стоячие волны возникают при отражении волн от преград. Падающая на преграду волна и бегущая ей навстречу отраженная волна, налагаясь друг на друга, дают стоячую волну. В каждой точке стоячей волны происходят колебания той же частоты, что и у встречных волн. Амплитуда колебаний является периодической функцией
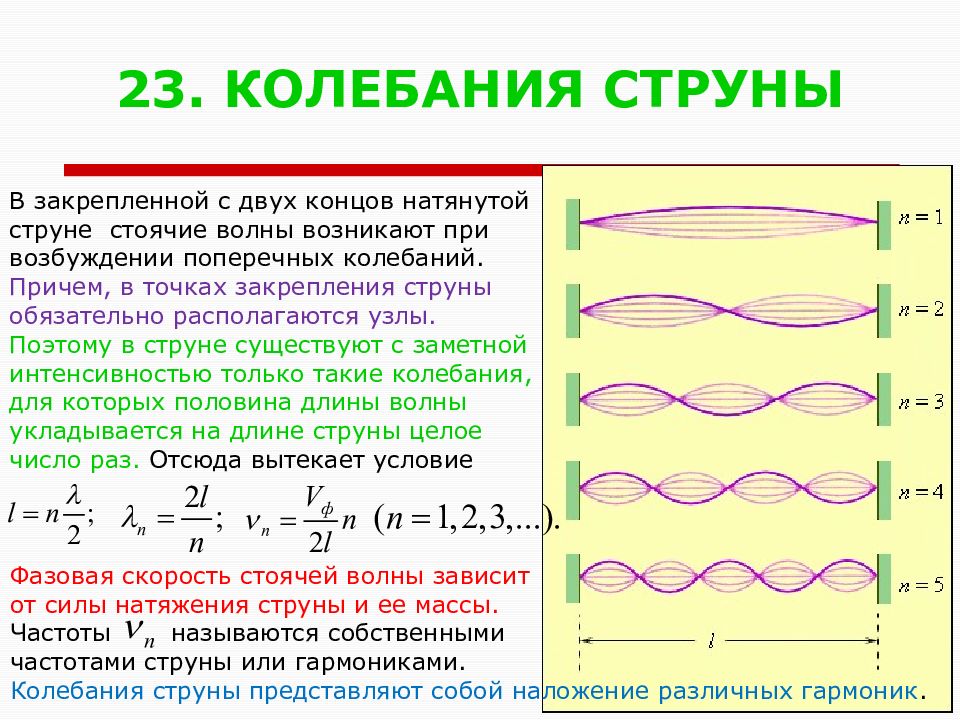
Слайд 24: 23. КОЛЕБАНИЯ СТРУНЫ
В закрепленной с двух концов натянутой струне стоячие волны возникают при возбуждении поперечных колебаний. Причем, в точках закрепления струны обязательно располагаются узлы. Поэтому в струне существуют с заметной интенсивностью только такие колебания, для которых половина длины волны укладывается на длине струны целое число раз. Отсюда вытекает условие Фазовая скорость стоячей волны зависит от силы натяжения струны и ее массы. Частоты называются собственными частотами струны или гармониками. Колебания струны представляют собой наложение различных гармоник.
Слайд 25: 24. ЗВУК
Упругие волны в воздухе, имеющие частоту в пределах от 16 Гц до 20 кГц вызывают в ушах человека ощущение звука. Поэтому упругие волны в любой среде, имеющие частоту в этом диапазоне, называют звуковыми волнами или просто звуком. Упругие волны с частотами, меньшими 16 Гц, называют инфразвуком; волны с частотами больше 20 кГц, называют ультразвуком. Воспринимаемые звуки люди различают по высоте (частоте), тембру (акустическому спектру) и громкости (интенсивности волны).
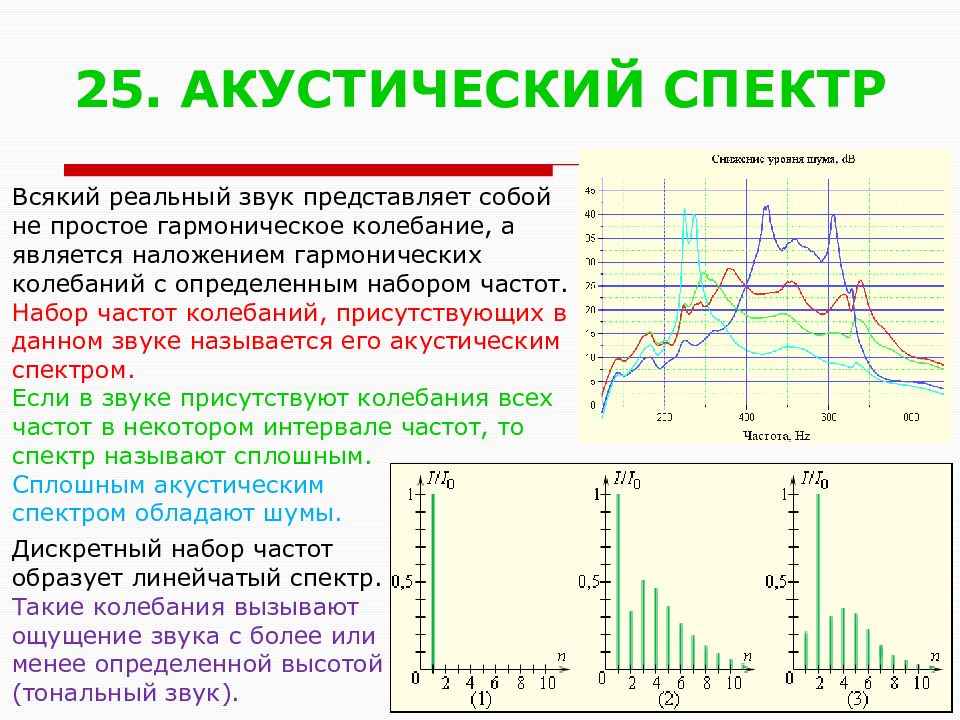
Слайд 26: 25. АКУСТИЧЕСКИЙ СПЕКТР
Всякий реальный звук представляет собой не простое гармоническое колебание, а является наложением гармонических колебаний с определенным набором частот. Набор частот колебаний, присутствующих в данном звуке называется его акустическим спектром. Если в звуке присутствуют колебания всех частот в некотором интервале частот, то спектр называют сплошным. Сплошным акустическим спектром обладают шумы. Дискретный набор частот образует линейчатый спектр. Такие колебания вызывают ощущение звука с более или менее определенной высотой (тональный звук).
Слайд 27: 26. ТЕМБР ЗВУКА
Высота тонального звука зависит от основной (наименьшей) частоты в акустическом спектре. Относительная интенсивность обертонов, то есть колебаний с более высокими частотами, определяет окраску или тембр звукового сигнала. Различный спектральный состав звуков, возбуждаемых разными музыкальными инструментами, позволяет отличить на слух, например, гитару от скрипки или рояля.
Слайд 28: 27. ГРОМКОСТЬ ЗВУКА
Уровень громкости определяется как десятичный логарифм отношения интенсивности данного звука к ин- тенсивности на пороге слышимости.
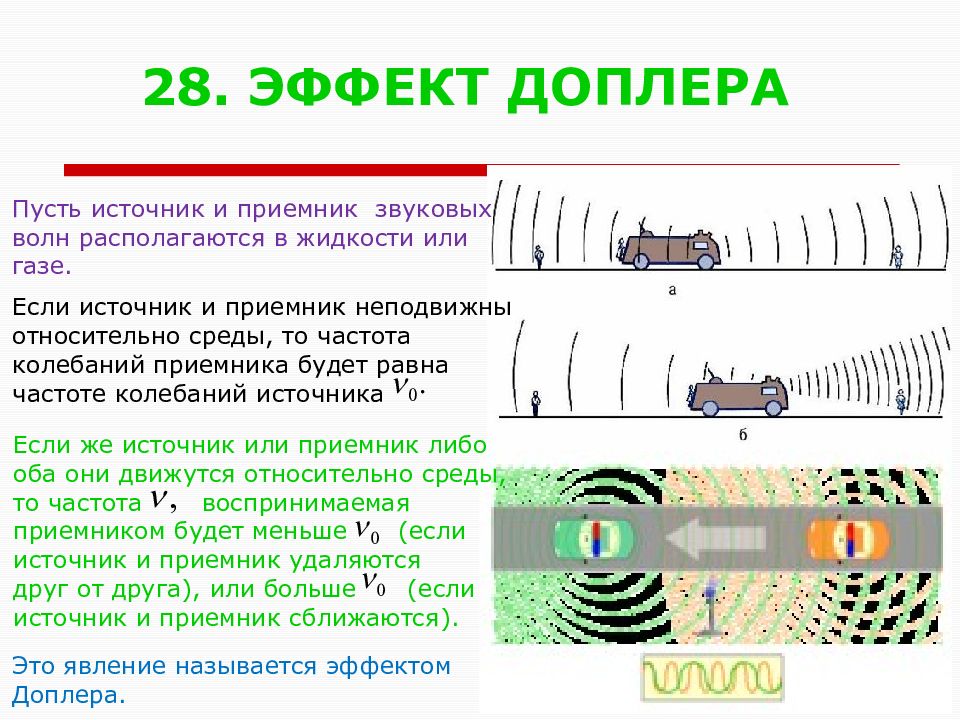
Слайд 29: 28. ЭФФЕКТ ДОПЛЕРА
Пусть источник и приемник звуковых волн располагаются в жидкости или газе. Если источник и приемник неподвижны относительно среды, то частота колебаний приемника будет равна частоте колебаний источника Если же источник или приемник либо оба они движутся относительно среды, то частота воспринимаемая приемником будет меньше (если источник и приемник удаляются друг от друга), или больше (если источник и приемник сближаются). Это явление называется эффектом Доплера.
Слайд 30: 29. ДВИЖЕНИЕ ИСТОЧНИКА
Если источник неподвижен и колеблется с частотой то через одну секунду, когда источник будет совершать -е колебание, порожденный первым колебанием «гребень» волны успеет пройти в среде путь, численно равный фазовой скорости волны Пусть теперь источник движется относительно среды со скоростью Скорость источника будем считать положительной, если источник движется по направлению к приемнику (наблюдателю), и отрицательной, если источник движется в направлении от источника (наблюдателя). Когда источник будет завершать -е колебание (через одну секунду), «гребень», порождаемый первым колебанием будет находиться на расстоянии численно равном Следовательно, «гребней» и «впадин» волны должны уместиться на длине так что длина волны, воспринимаемой наблюдателем, будет
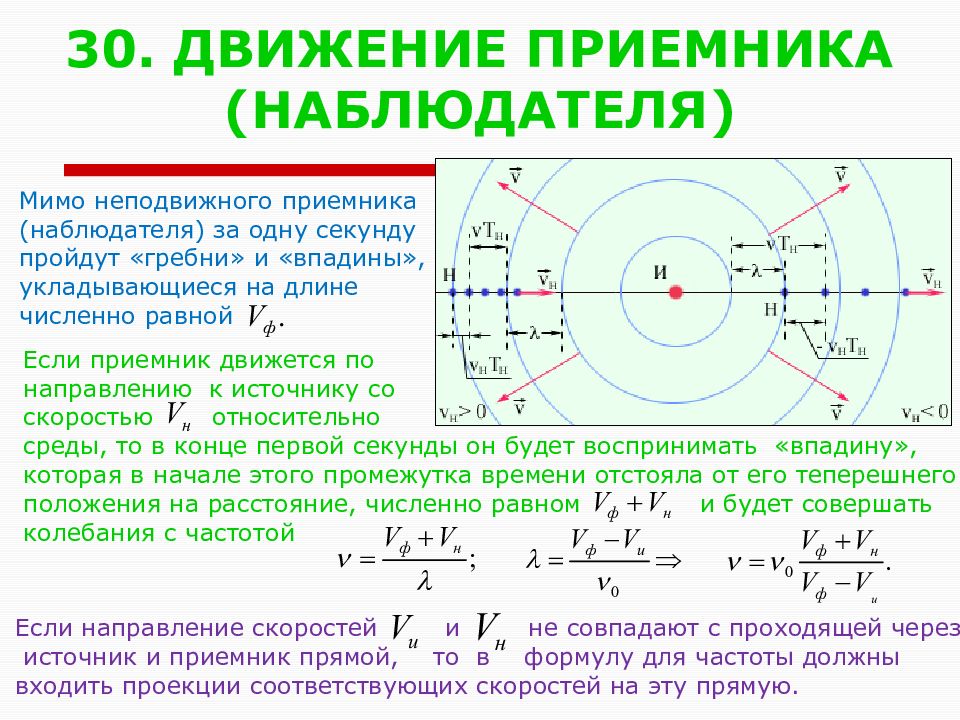
Слайд 31: 30. ДВИЖЕНИЕ ПРИЕМНИКА (НАБЛЮДАТЕЛЯ)
Мимо неподвижного приемника (наблюдателя) за одну секунду пройдут «гребни» и «впадины», укладывающиеся на длине численно равной Если приемник движется по направлению к источнику со скоростью относительно среды, то в конце первой секунды он будет воспринимать «впадину», которая в начале этого промежутка времени отстояла от его теперешнего положения на расстояние, численно равном и будет совершать колебания с частотой Если направление скоростей и не совпадают с проходящей через источник и приемник прямой, то в формулу для частоты должны входить проекции соответствующих скоростей на эту прямую.
Слайд 33: 1. УРАВНЕНИЯ МАКСВЕЛЛА
Перепишем уравнения Максвелла с учетом материальных уравнений: В случае однородной нейтральной непроводящей среды уравнения примут вид:
Слайд 34: 2. ВОЛНОВОЕ УРАВНЕНИЕ
Для однородной нейтральной непроводящей среды система уравнений Максвелла имеет вид Возьмем ротор от обеих частей уравнения (1): Воспользуемся выражением для ротора из уравнения (3): Раскроем двойное векторное произведение с учетом уравнения (4):
Слайд 35: 3. СКОРОСТЬ ЭМВ
Для однородной нейтральной непроводящей среды получено волновое уравнение Электрическая и магнитная постоянные связаны простым соотношением со скоростью света в вакууме При этом волновое уравнения для напряженности электрического поля и аналогичное для напряженности магнитного поля принимают вид: Полученные волновые уравнения неразрывно связаны между собой, т.к. они получены из уравнений Максвелла, которые одновременно содержат напряженности и электрического и магнитного полей. Из этих волновых уравнений следует, что электромагнитные поля могут существовать в виде электромагнитных волн, фазовая скорость которых равна
Слайд 36: 4. УРАВНЕНИЯ МАКСВЕЛЛА ДЛЯ ПЛОСКОЙ ЭМВ (I)
Перепишем уравнения Максвелла для однородной нейтральной непроводящей среды в координатной форме: Направим ось x перпендикулярно волновым поверхностям плоской ЭМВ. Тогда векторы и а значит, и их проекции на координатные оси не будут зависеть от координат y и z. То есть и
Слайд 37: 4. УРАВНЕНИЯ МАКСВЕЛЛА ДЛЯ ПЛОСКОЙ ЭМВ (II)
Упростим систему уравнения Максвелла для однородной нейтральной диэлектрической (непроводящей) среды для случая плоской волны распространяющей вдоль оси x. При этом пропадает зависимость всех компонент поля от поперечных координат y и z. Поэтому система уравнений упрощается к виду:
Слайд 38: 4. УРАВНЕНИЯ МАКСВЕЛЛА ДЛЯ ПЛОСКОЙ ЭМВ (III)
Выпишем в координатной форме систему уравнений Максвелла для плоской волны, распространяющейся вдоль оси x в однородной нейтральной диэлектрической (непроводящей) среде Уравнение (4) и первое из уравнений (3) показывают, что не может зависеть ни от x, ни от t. Уравнение (2) и первое из уравнений (1) дают такой же результат для Следовательно, отличные от нуля и могут быть обусловлены лишь постоянными однородными полями, накладывающимися на электромагнитные волны. Само поле волны не имеет составляющих вдоль оси x. Отсюда вытекает, что векторы и перпендикулярны к направлению распространения волны, то есть что электромагнитные волны в однородном диэлектрике поперечны.
Слайд 39: 7. УРАВНЕНИЯ МАКСВЕЛЛА ДЛЯ ПЛОСКОЙ ЭМВ (IV)
Предполагая отсутствие постоянных (стационарных) полей запишем упрощенную систему уравнений Максвелла для плоской ЭМВ, распространяющейся вдоль оси x однородной нейтральной непроводящей (диэлектрической) среды: Можно заметить, что оставшиеся 4 уравнения объединяются в две независимые группы: Первая группа уравнений связывает компоненты и а вторая – компоненты и Если в пространстве было создано переменное электрическое поле то оно будет порождать переменное магнитное поле которое в свою очередь создаст переменное электрическое поле Поля и при этом не возникают.
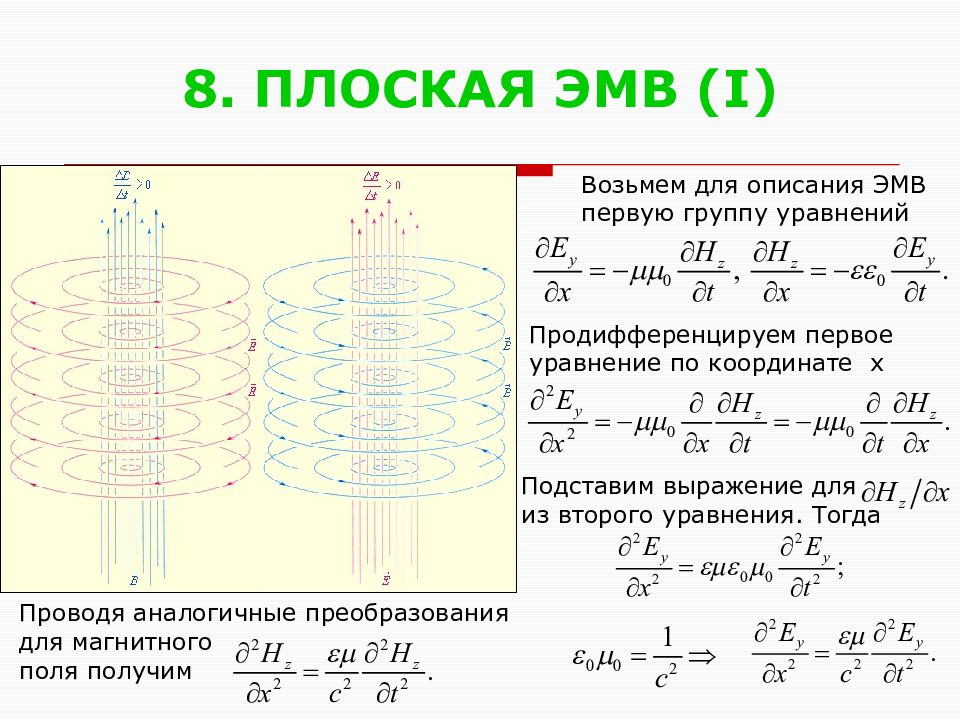
Слайд 40: 8. ПЛОСКАЯ ЭМВ ( I)
Возьмем для описания ЭМВ первую группу уравнений Продифференцируем первое уравнение по координате x Подставим выражение для из второго уравнения. Тогда Проводя аналогичные преобразования для магнитного поля получим
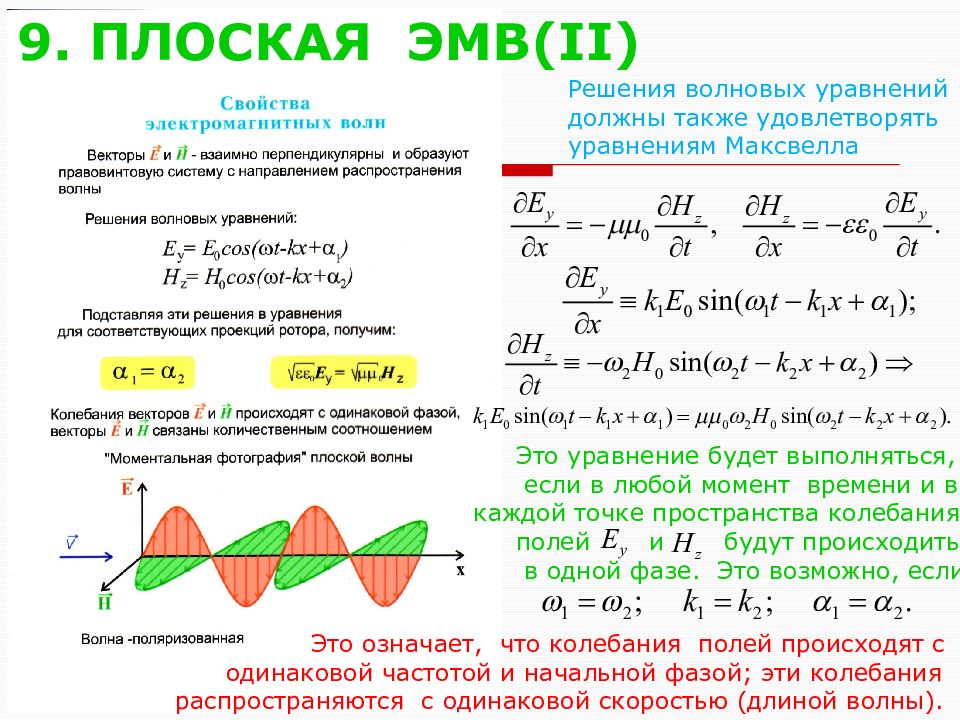
Слайд 41: 9. ПЛОСКАЯ ЭМВ( II)
Решения волновых уравнений должны также удовлетворять уравнениям Максвелла Это уравнение будет выполняться, если в любой момент времени и в каждой точке пространства колебания полей и будут происходить в одной фазе. Это возможно, если Это означает, что колебания полей происходят с одинаковой частотой и начальной фазой; эти колебания распространяются с одинаковой скоростью (длиной волны).
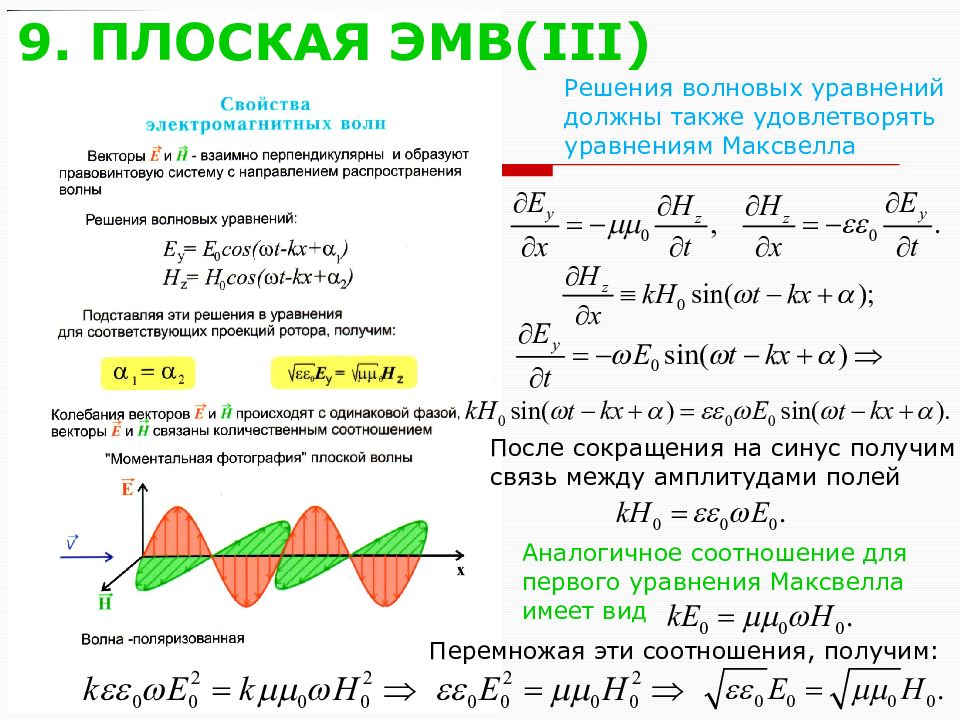
Слайд 42: 9. ПЛОСКАЯ ЭМВ( III)
Решения волновых уравнений должны также удовлетворять уравнениям Максвелла После сокращения на синус получим связь между амплитудами полей Аналогичное соотношение для первого уравнения Максвелла имеет вид Перемножая эти соотношения, получим:
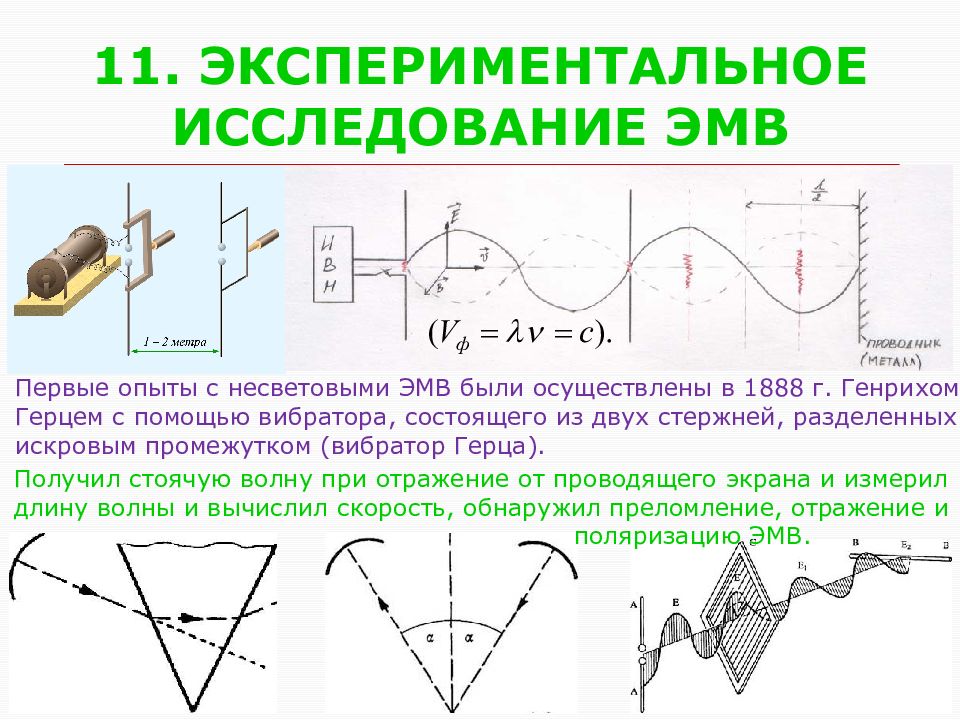
Слайд 43: 11. ЭКСПЕРИМЕНТАЛЬНОЕ ИССЛЕДОВАНИЕ ЭМВ
Первые опыты с несветовыми ЭМВ были осуществлены в 1888 г. Генрихом Герцем с помощью вибратора, состоящего из двух стержней, разделенных искровым промежутком (вибратор Герца). Получил стоячую волну при отражение от проводящего экрана и измерил длину волны и вычислил скорость, обнаружил преломление, отражение и поляризацию ЭМВ.
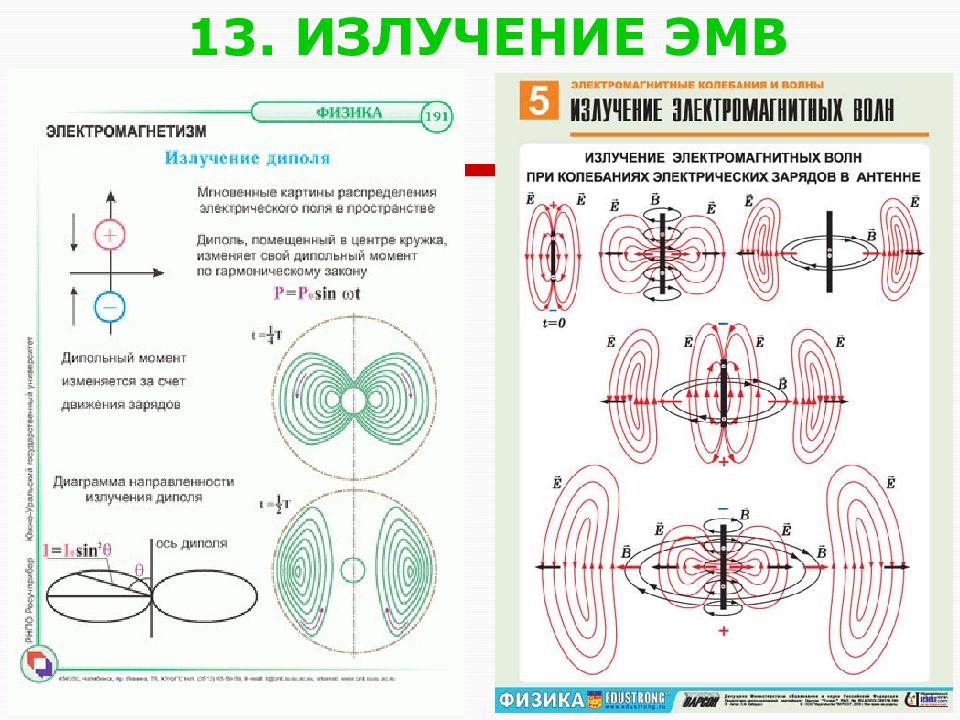
Слайд 44: 12. ЭНЕРГИЯ ЭМВ
Электромагнитные волны переносят энергию. Плотность потока энергии волны можно получить, умножив ее объемную плотность энергии на фазовую скорость. Плотность энергии ЭМВ слагается из плотности энергии электрического и магнитного поля: Вектор Пойнтинга является аналогом вектора Умова для механических волн.