Подготовила Жураева Вазира
Критерий Колмогорова-Смирнова – непараметрический критерий согласия, в классическом понимании предназначен для проверки простых гипотез о принадлежности анализируемой выборки некоторому известному закону распределения. Наиболее известно применение данного критерия для проверки исследуемых совокупностей на нормальность распределения.
Критерий Колмогорова-Смирнова был разработан советскими математиками Андреем Николаевичем Колмогоровым и Николаем Васильевичем Смирновым. Колмогоров А.Н. (1903-1987) - Герой Социалистического Труда, профессор Московского государственного университета, академик АН СССР - крупнейший математик XX века, является одним из основоположников современной теории вероятности. Смирнов Н.В. (1900-1966)- член-корреспондент АН СССР, один из создателей непараметрических методов математической статистики и теории предельных распределений порядковых статистик. Впоследствии критерий согласия Колмогорова-Смирнова был доработан с целью применения для проверки совокупностей на нормальность распределения американским статистиком, профессором Университета Джорджа Вашингтона Хьюбертом Лиллиефорсом ( Hubert Whitman Lilliefors, 1928-2008). Профессор Лиллиефорс являлся одним из пионеров применения компьютерной техники в статистических расчётах.
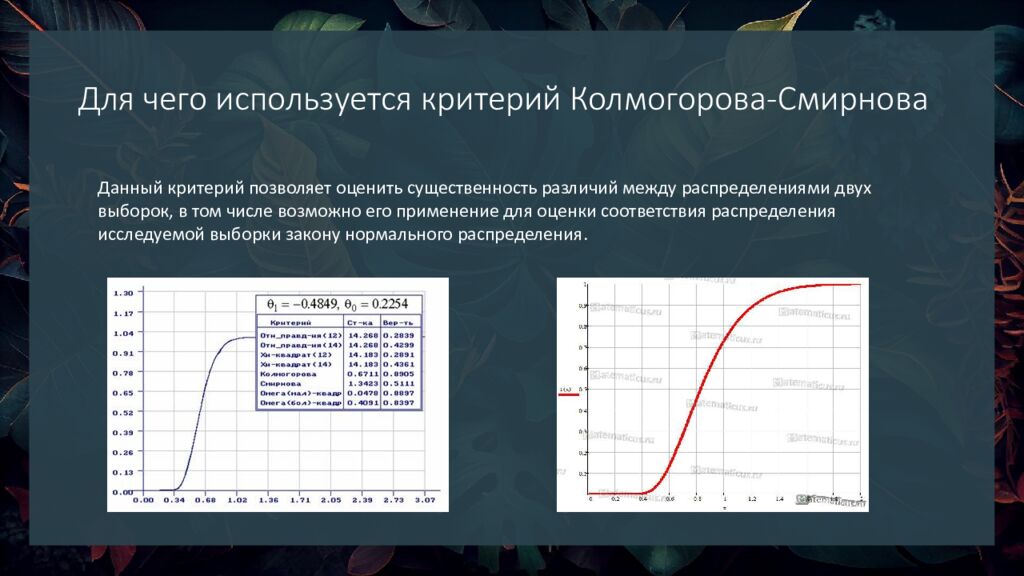
Данный критерий позволяет оценить существенность различий между распределениями двух выборок, в том числе возможно его применение для оценки соответствия распределения исследуемой выборки закону нормального распределения.
Критерий Колмогорова-Смирнова предназначен для проверки на нормальность распределения совокупностей количественных данных. Для большей достоверности полученных данных объемы рассматриваемых выборок должен быть достаточно большими: n ≥ 50. При размерах оцениваемой совокупности от 25 до 50 элементов, целесообразно применение поправки Большева.
Критерий Колмогорова-Смирнова рассчитывается при помощи специальных статистических программ. В основе лежит статистика вида: где sup S - точная верхняя грань множества S, Fn - функция распределения исследуемой совокупности, F(x) - функция нормального распределения Выводимые значения вероятности основаны на предположении, что среднее и стандартное отклонение нормального распределения известны априори и не оцениваются из данных. Однако на практике обычно параметры вычисляются непосредственно из данных. В этом случае критерий нормальности включает сложную гипотезу ("насколько вероятно получить D статистику данной или большей значимости, зависящей от среднего и стандартного отклонения, вычисленных из данных"), и приводятся вероятности Лиллиефорса (Lilliefors, 1967).
Если D статистика Колмогорова-Смирнова значима (p<0,05), то гипотеза о том, что соответствующее распределение нормально, должна быть отвергнута.
