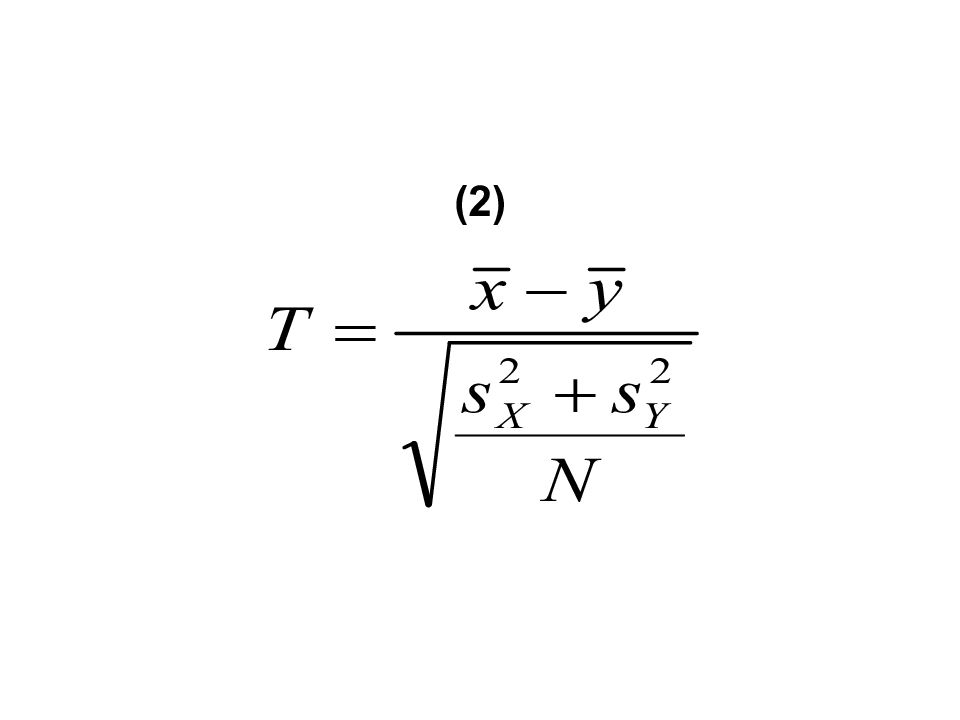ПРОВЕРКА ГИПОТЕЗ
Выборки из генеральной совокупности делаются случайным образом. – Они могут быть разных объемов, различного состава, с разными значениями параметров. Наиболее важные общие вопросы : КАКОМУ ТЕОРЕТИЧЕСКОМУ РАСПРЕДЕЛЕНИЮ СООТВЕТСТВУЮТ ВЫБОРКИ ? СЛУЧАЙНО ЛИ РАСХОЖДЕНИЕ ПАРАМЕТРОВ ?
Вопрос можно поставить так, что он будет допускать один из двух противоположных ответов. Например: Является ли нормальным распределение? – Либо является, либо нет. Ответ важен, так как многие формулы и закономерности выведены именно для нормального распределения.
При исследовании двух выборок выяснилось, что их средние отличаются. Является ли это различие существенным или оно случайно? – Один вариант - является, тогда выборки сделаны из разных генеральных совокупностей. Второй - не является, тогда различие случайно, и выборки на самом деле сделаны из одной и той же генеральной совокуп- ности. Ответ важен, так как часто это вопрос об эффективности лечения.
Выдвижение нулевой гипотезы, то есть исходного предположения. Построение критерия его проверки. КРИТЕРИЙ – случайная величина, значения которой зависят от значений сравниваемых параметров.
Вычисление двух значений критерия : наблюдаемого и критического. Наблюдаемое значение вычисляется по резуль- татам исследования выборки. Критическое значение определяется по надежности (иногда учитывается еще какой-то параметр выборки).
Сравнение наблюдаемого и критического значений. По результатам сравнения – нулевая гипотеза принимается или отвергается. Это решение принимается с данной надежностью (из которой исходили при определении критического значения).
Выбор критерия определяется конкретной задачей. Так, для решения вопроса о нормальности распределения можно использовать критерий χ 2 ( хи-квадрат), или критерий согласия Пирсона. Существует большая группа критериев согласия. Они называются так потому, что позволяют решить, согласуется ли выдвинутая гипотеза с экспериментальными данными.
Мы рассмотрим подробно уже упоминавшуюся задачу оценки достоверности различия выборочных средних.
Пусть X и Y – однотипные признаки. (Например, артериальное давление у группы пациентов до и после лечения.) Средние выборочные этих величин оказались различны : x ≠ y. Вопрос : достоверно или нет это различие ? Иными словами : различны или равны их теоретические средние μ X и μ Y ?
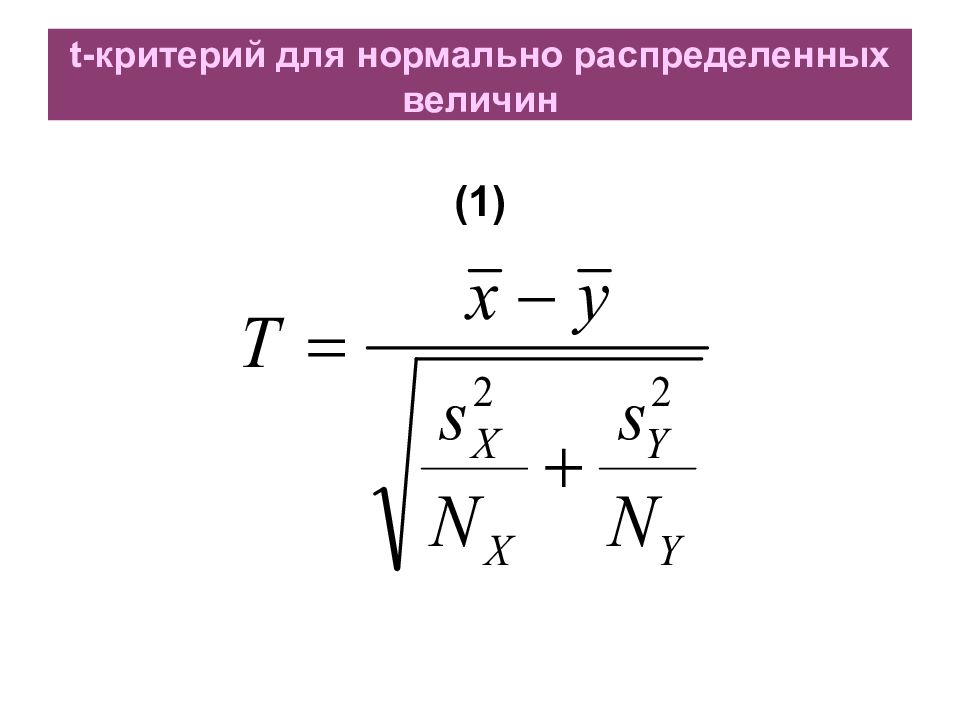
Этот вопрос может иметь в медицине принципиальное значение. Так, в примере с артери-альным давлением ответ « μ X ≠ μ Y » означает эффектив- ность проведенного лечения. Если же μ X = μ Y, то лечение было неэффективно. Нулевая гипотеза : теоретические средние величин X и Y равны, μ X = μ Y. Критерий : в случае нормального распределения X и Y - t- критерий следующего вида :
(1)
Здесь x, s 2 X, y, s 2 Y – средние значения и исправленные дисперсии выборок для двух исследуемых величин, N X и N Y – объемы этих выборок. Если объемы двух выборок равны, N X = N Y = N, формула упрощается :
(2)
Подставляя в форму- лу (1) или (2) значения параметров выборок, находим наблюдаемое значение случайной величины T. Оно тем меньше, чем меньше различаются средние выборочные. Очевидно, чем меньше различие средних выборочных, тем меньше и различие средних теоретических. t- критерий характеризу- ет близость математи- ческих ожиданий двух случайных величин.
При больших объемах выборок можно считать распределение Т (как и величин Х и Y ) нормальным. Тогда по заданной надежности находим Φ ( t кр ) : 1 + γ Φ ( t кр ) = 2 и далее само критическое значение Т – по таблице нормального распределения. Теперь сравниваем модуль наблюдаемого значения величины Т и ее критическое значение.
Если ׀ t набл ׀ < t кр, гипотезу о равенстве теоретических сред- них принимают, и делают вывод, что различие средних выборочных случайно. Если же ׀ t набл ׀ > t кр, то нулевую гипотезу отвергают, и делают вывод, что различие средних выборочных значимо, существенно.
В первые сутки болезни гриппом заме- рена температура Х у 60 больных, прошедших предварительную вакцинацию, и температура Y у 60 больных, не прошедших вакцинации. Обработка статистических рядов дала результаты : x = 38,3; y = 38,9; s 2 X = 0,33; s 2 Y = 0,29. Проверить достоверность различия выборочных средних на уровне значимости 0,05.
Используем t -критерий. Ищем наблюдаемое значение T: 38,3 – 38,9 t набл = √ (0,33 + 0,29) / 60 - 0,6 = √ 0,012 Ищем критическое значение Т : γ = 1 – β = 1 – 0,05 = 0,95 ; Φ ( t кр ) = 0,975 ; t кр ≈ 2. Сравниваем : ׀ t набл ׀ ≈ 5,45 > 2. Вывод : различие средних температур существенно (с надежностью 95%). ≈ - 5,45
