Метрологические характеристики СИ
Метрологические характеристики СИ (МХ СИ) - характеристики свойств СИ, оказывающих влияние на результаты и погрешности измерений, предназначенные для оценки технического уровня и качества СИ, для определения результатов измерений и расчетной оценки характеристик инструментальной составляющей погрешности измерений. Нормирование МХ - количественное задание определенных значений характеристик и допустимых отклонений от этих значений. Нормируемые МХ указывают в нормативно-технической документации (НТД) на СИ
А. Характеристики, предназначенные для определения результатов измерений (номинальные МХ) Под термином «номинальный» понимают определенное значение чего-либо, не учитывающее влияние внешних факторов Номинальная МХ СИ - значение, задаваемое изготовителем для определенных условий работы СИ
А1. Номинальные МХ однозначных и многозначных мер - значения мер, представляемые именованными числами Для пипеток с одной меткой и градуированных - номинальная вместимость
А2. МХ аналоговых приборов и многозначных мер
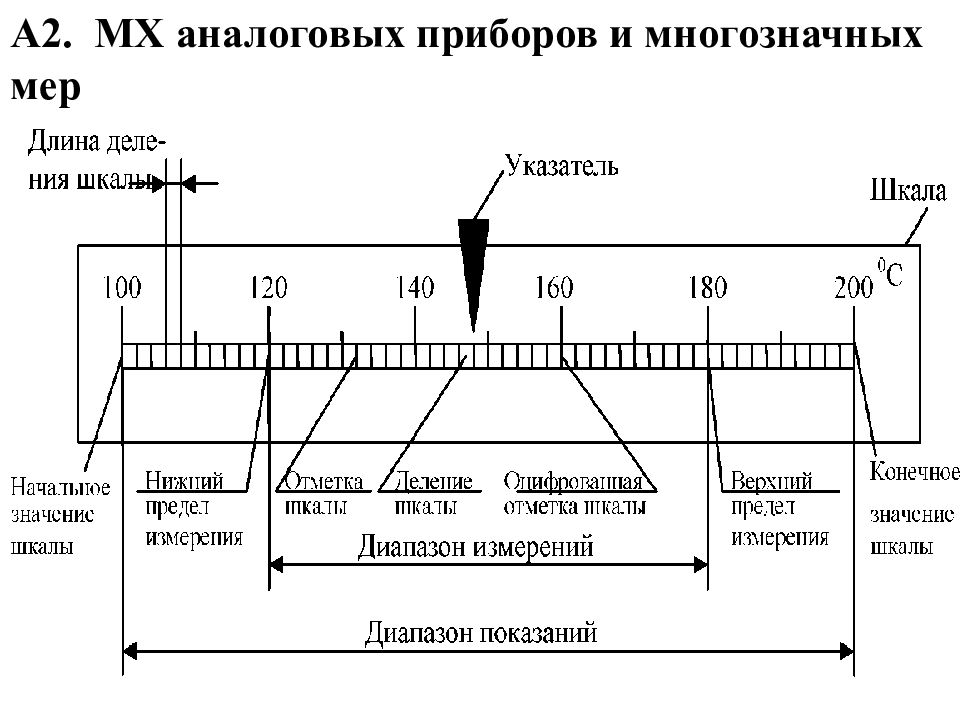
•• Цена деления шкалы – разность значений величины, соответствующих двум соседним отметкам шкалы •• Диапазон показаний – область значений шкалы, ограниченная конечным (наибольшим) и начальным (наименьшим) значениями ФВ, указанными на шкале. •• Диапазон измерений – область значений измеряемой величины, для которой нормирована погрешность средства измерений. •• Предел измерений – наибольшее или наименьшее значение диапазона измерений.
А 3. МХ цифровых приборов •• Вид выходного кода (десятичный) •• Число разрядов кода - предельное число знаков на табло •• Наличие разделительной десятичной запятой (точки), минуса и др. •• Цена единицы наименьшего разряда цифровых СИ
А4. Функция преобразования СИ ( ИзУ ) или градуировочная характеристика Градуировочная характеристика СИ – зависимость между значениями входной и выходной величин СИ Y = kX, где X - значение величины входного сигнала, Y - значение величины выходного сигнала, k - коэффициент пропорциональности.
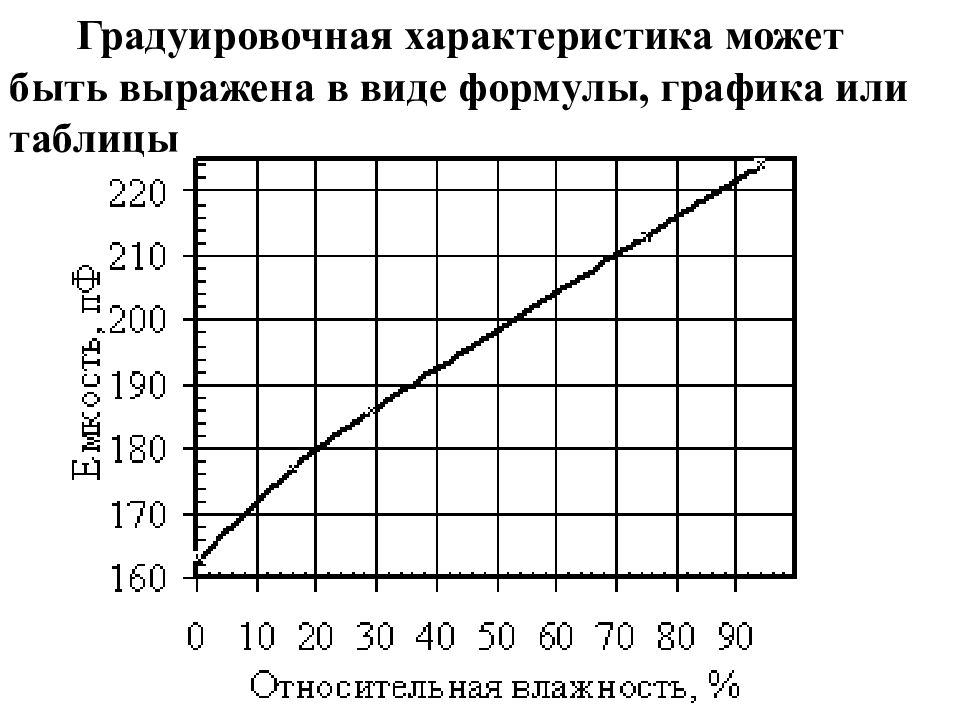
Градуировочная характеристика может быть выражена в виде формулы, графика или таблицы
А5. Характеристики чувствительности ИзУ ‒ Чувствительность ИзУ - отношение изменения выходной величины к вызывающему его изменению входной величины. Чувствительность S представляет собой способность ИзУ реагировать на изменение входного сигнала :
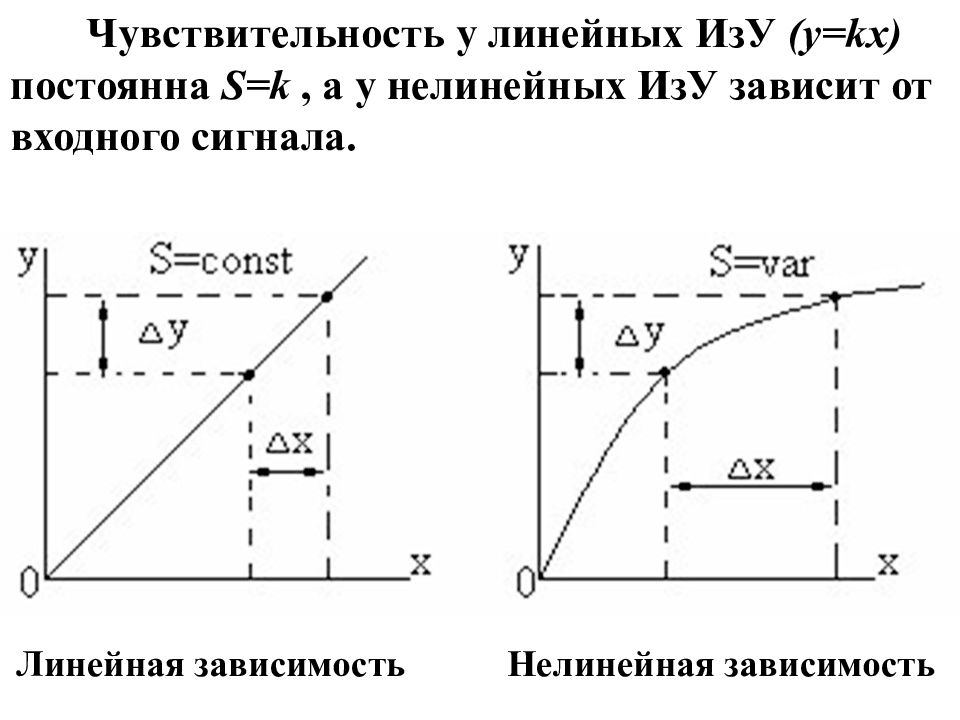
Чувствительность у линейных ИзУ ( y = kх ) постоянна S=k, а у нелинейных ИзУ зависит от входного сигнала. Линейная зависимость Нелинейная зависимость
‒ Порог чувствительности - наименьшее значение входной величины, которое можно обнаружить с помощью данного ИзУ. ‒ Разрешающая способность ИзУ - наименьшее различаемое с помощью данного ИзУ изменение измеряемой величины
Влияющие величины ‒ внешние физические воздействия, оказывающие влияние на МХ СИ: Температура и влажность воздуха, Атмосферное давление, Частота и напряжение питания и пр. Нормальные условия, при которых влияющие на результаты измерения величины находятся в установленных пределах Нормальные условия эксплуатации указывают в НТД, регламентирующих правила испытания и эксплуатации данного СИ В. Характеристики чувствительности СИ к условий применения
В паспортах или технических условиях (ТУ) на СИ обычно указывают области значений влияющих величин, например: температура воздуха от 15 до 25 °С, о тносительная влажность воздуха от 45 до 75 %, атмосферное давление от 740 до 760 мм рт. ст.
С. Динамические характеристики СИ Динамические МХ СИ возникают при динамическом режиме его работы, при котором СИ воспринимает изменение входной величины и размеры измеряемой величины изменяются во времени. Динамические характеристики СИ описывают инерционные свойства СИ и определяют время установления показаний прибора от момента скачкообразного изменения измеряемой величины до момента установления показания, соответствующего новому значению измеряемой величины.
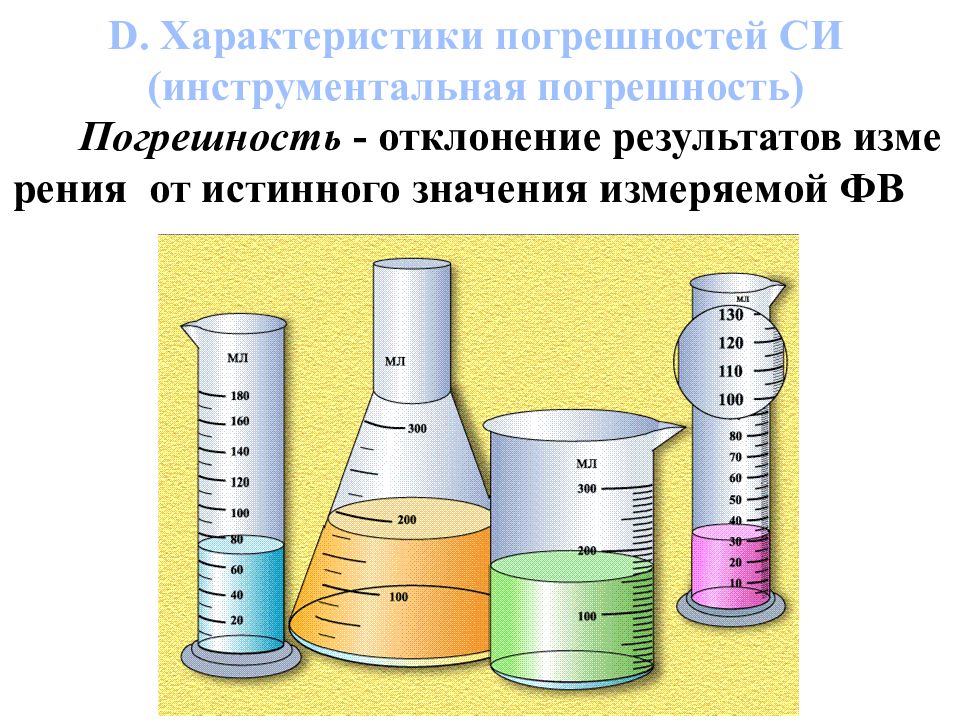
D. Характеристики погрешностей СИ (инструментальная погрешность) Погрешность - отклонение результатов измерения от истинного значения измеряемой ФВ
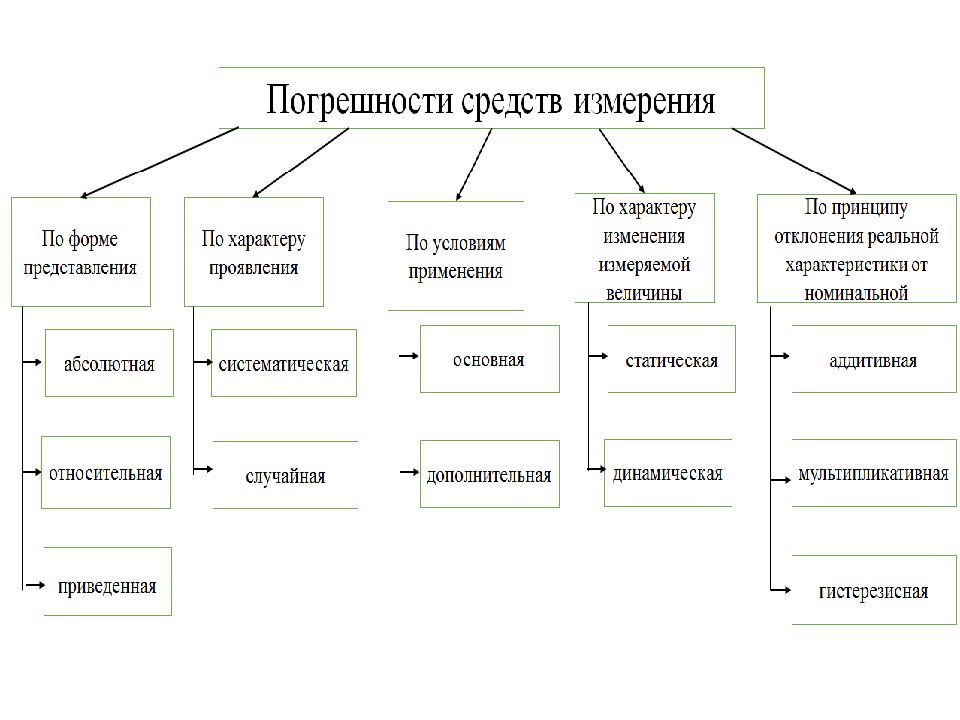
D1. По форме представления погрешности Абсолютная погрешность СИ (∆) - разность между измеренным Х и (показания СИ) и истинным (действительным) Х д значениями измеряемой величины ∆ = Х и – Х Д, Абсолютная погрешность СИ выражается как где ∆ - предел допустимой абсолютной погрешности, выраженной в единицах величины; а- именованное положительное число, выраженное в тех же единицах.
Относительная погрешность СИ (δ) – отношение абсолютной погрешности прибора к истинному значению измеряемой величины: Приведенная погрешность СИ (γ ) – это отношение абсолютной погрешности к нормирующему значению: γ – предел допустимой приведенной погрешности, %;
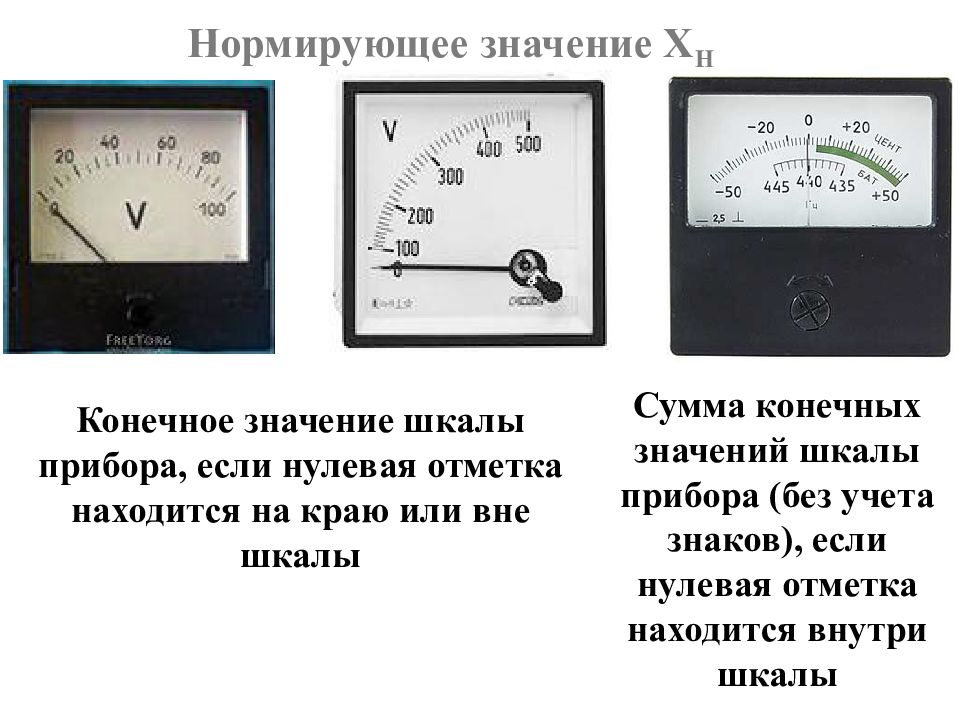
Нормирующее значение Х Н Конечное значение шкалы прибора, если нулевая отметка находится на краю или вне шкалы Сумма конечных значений шкалы прибора (без учета знаков), если нулевая отметка находится внутри шкалы
D2. По характеру проявления систематическая погрешность измерения -составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при измерении одной и той же величины случайная погрешность измерения - составляющая погрешности измерения, изменяющаяся случайным образом при повторном измерении одной и той же величины
основная погрешность СИ - погрешность, которая получается при использовании его в нормальных условиях дополнительная погрешность СИ - погрешность, вызванная отклонением одной из влияющих величин от ее нормативного значения D3. По условиям применения
D 4. По характеру измерения измеряемой величины статическая погрешность – это погрешность СИ, возникающие при измерении неизменных во времени величин; динамическая погрешность – это погрешность СИ, возникающие при измерении изменяющихся во времени величин.
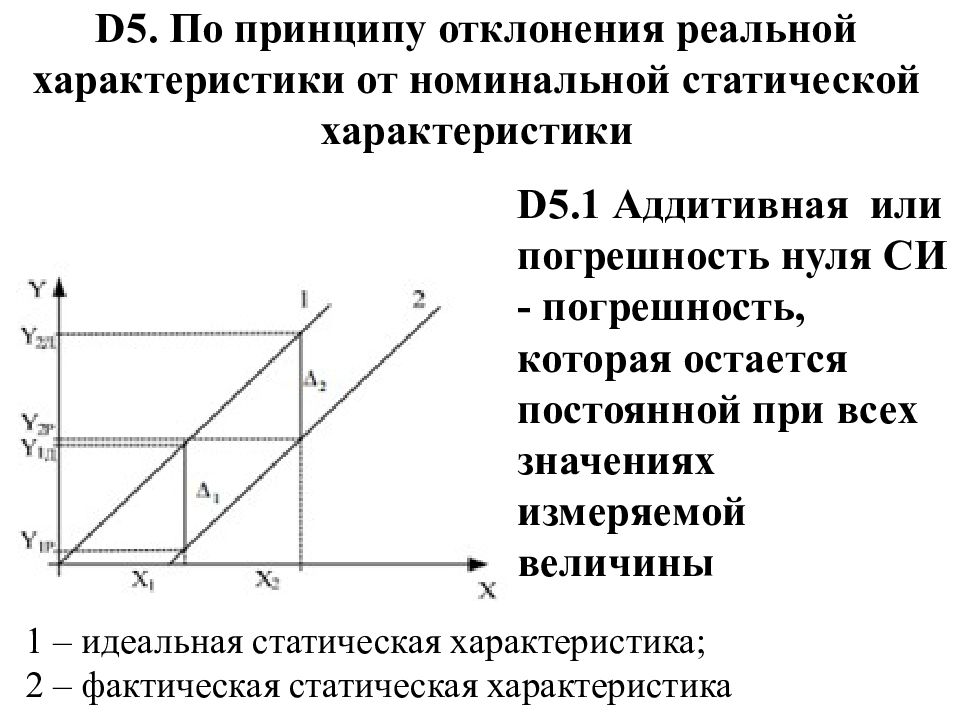
D 5. По принципу отклонения реальной характеристики от номинальной статической характеристики D5.1 Аддитивная или погрешность нуля СИ - погрешность, которая остается постоянной при всех значениях измеряемой величины 1 – идеальная статическая характеристика; 2 – фактическая статическая характеристика
D5/2. Мультипликативная или погрешность чувствительности СИ -погрешность, которая линейно возрастает (или убывает) с увеличением измеряемой величины D5.3. Погрешность гистерезиса или погрешность обратного хода, выражающаяся в несовпадении реальной функции преобразования СИ при увеличении (прямой ход) или уменьшении (обратный ход) измеряемой величины 1 – идеальная статическая характеристика; 2,3,4 – фактическая статическая характеристика
КЛАССЫ ТОЧНОСТИ СРЕДСТВ ИЗМЕРЕНИЙ
Класс точности СИ - обобщенная характеристика СИ, определяемая пределами допускаемых основных и дополнительных погрешностей, а также другими свойствами СИ, влияющими на точность осуществляемых с их помощью измерений.
СПОСОБЫ ЗАДАНИЯ КЛАССА ТОЧНОСТИ СИ
1-й способ ( используется для мер). Указывается порядковый номер класса точности меры. У станавливаются пределы допускаемых погрешностей в абсолютной форме (в единицах измеряемой величины). Предел допускаемой погрешности СИ- это наибольшая, без учета знака, погрешность СИ, при котором оно может быть признано и допущено к применению. Определение применимо к основной и дополнительной погрешности средств измерений. П огрешность определяют по технической документации (ГОСТ, ТУ).
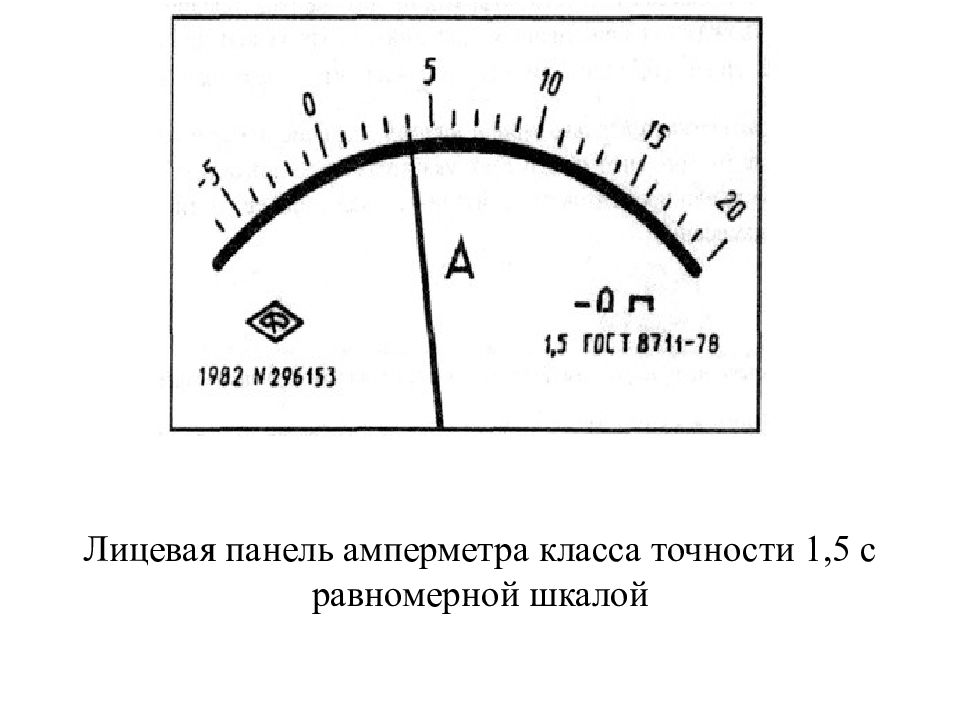
2-й способ (задание класса точности для СИ с преобладающими аддитивными погрешностями. Класс точности задаётся в виде числа К (без кружочка ). Нормируется основная приведённая погрешность γ х прибора, выраженная в процентах, которая во всех точках шкалы не должна превышать по модулю числа К, т.е. | γ х | ≤ К, %. Число К выбирается из ряда значений (1,0; 1,5; 2; 2,5; 4,0; 5,0; 6,0)⋅10 n, где n = 1, 0, –1, –2, ….
Лицевая панель амперметра класса точности 1,5 с равномерной шкалой
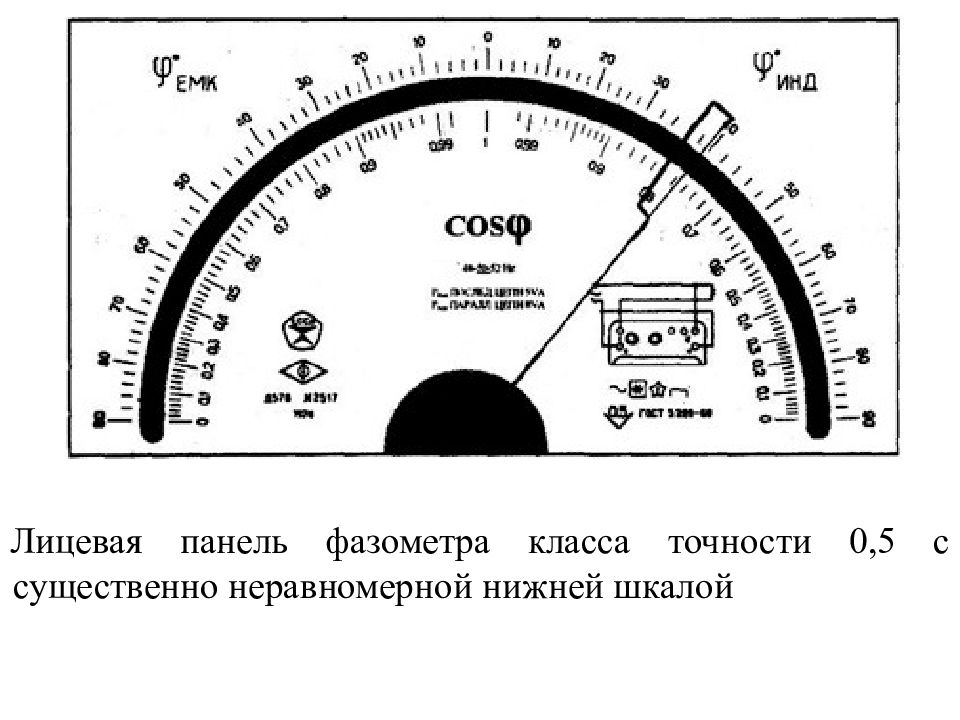
Для приборов с существенно неравномерной шкалой нормирующее значение Хн принимают равным всей длине шкалы или ее части, соответствующей диапазону измерении. Пределы приведенной погрешности выражают, как и длину шкалы, в единицах длины, а на средстве измерений класс точности условно обозначают в виде значка
Лицевая панель фазометра класса точности 0,5 с существенно неравномерной нижней шкалой
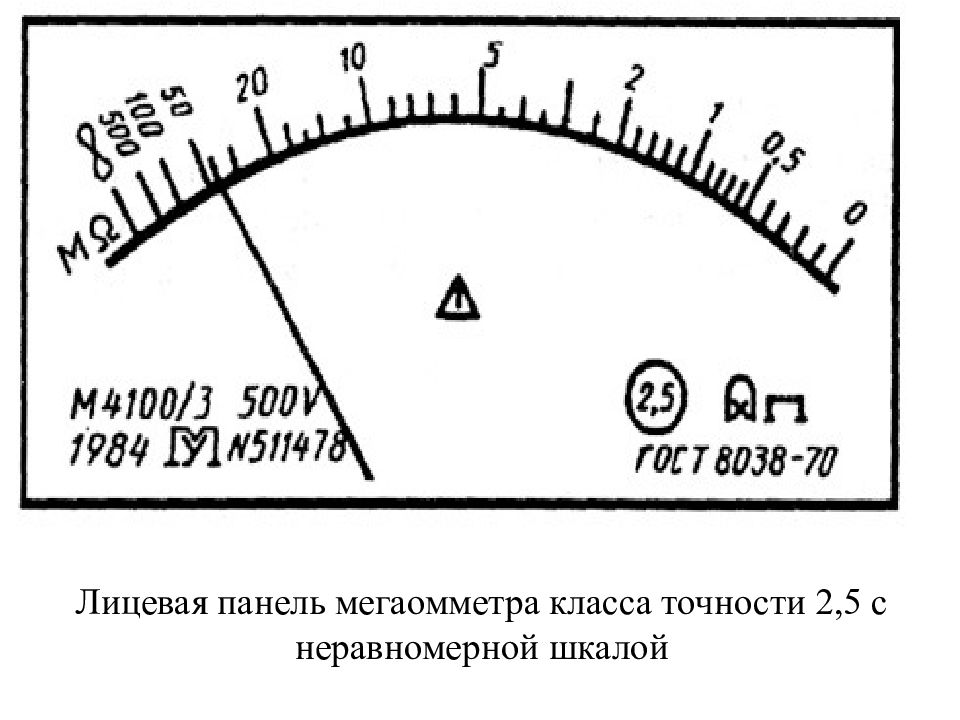
3-й способ (задание класса точности для ИП с преобладающими мультипликативными погрешностями). Нормируется основная относительная погрешность, выраженная в процентах, так что | δ X | ≤ К, %. Класс точности задаётся в виде числа К в кружочке К. Число К выбирается из приведённого выше ряда
Лицевая панель мегаомметра класса точности 2,5 с неравномерной шкалой
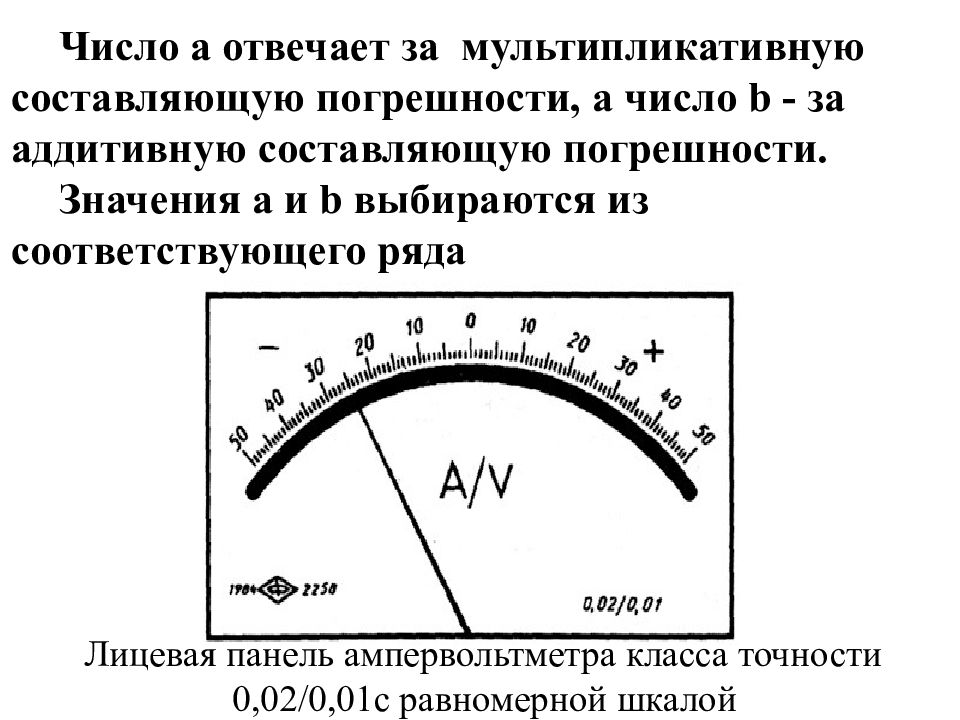
4-й способ (задание класса точности для приборов с соизмеримыми аддитивными и мультипликативными погрешностями). Класс точности задаётся двумя числами a / b, разделёнными косой чертой, причём a > b. Нормируется основная относительная погрешность, вычисляемая по формуле: где Xк - максимальное конечное значение пределов измерений; Х – показания прибора.
Число a отвечает за мультипликативную составляющую погрешности, а число b - за аддитивную составляющую погрешности. З начения a и b выбираются из соответствующего ряда Лицевая панель ампервольтметра класса точности 0,02/0,01с равномерной шкалой
