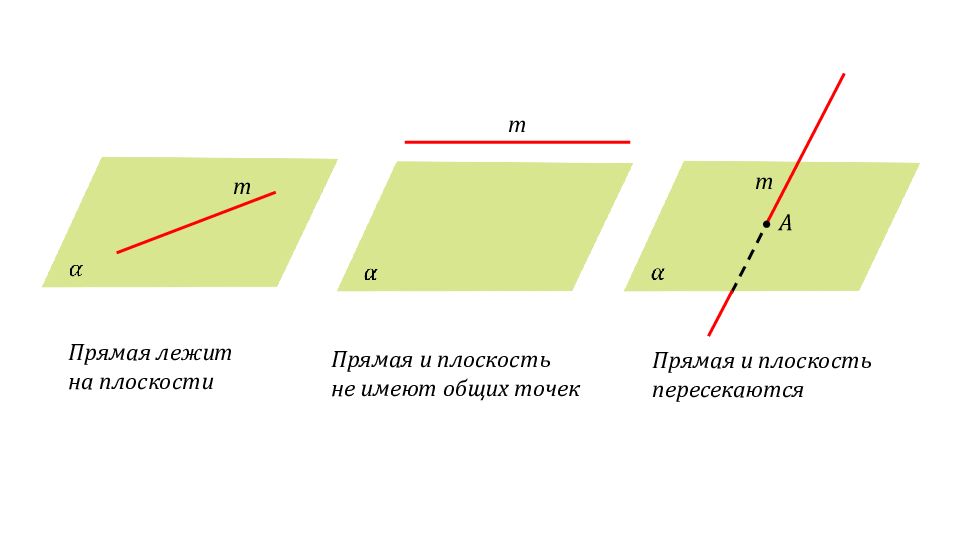
m m m A Прямая лежит на плоскости Прямая и плоскость не имеют общих точек Прямая и плоскость пересекаются
Прямая и плоскость называются параллельными, если они не имеют общих точек. Определение
Теорема 1 Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости. d Дано: Доказать: Доказательство. c
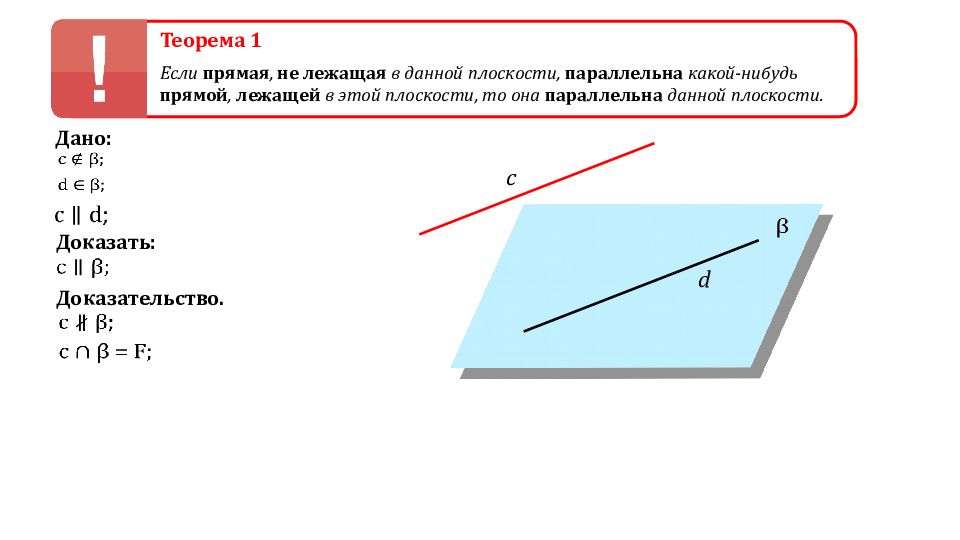
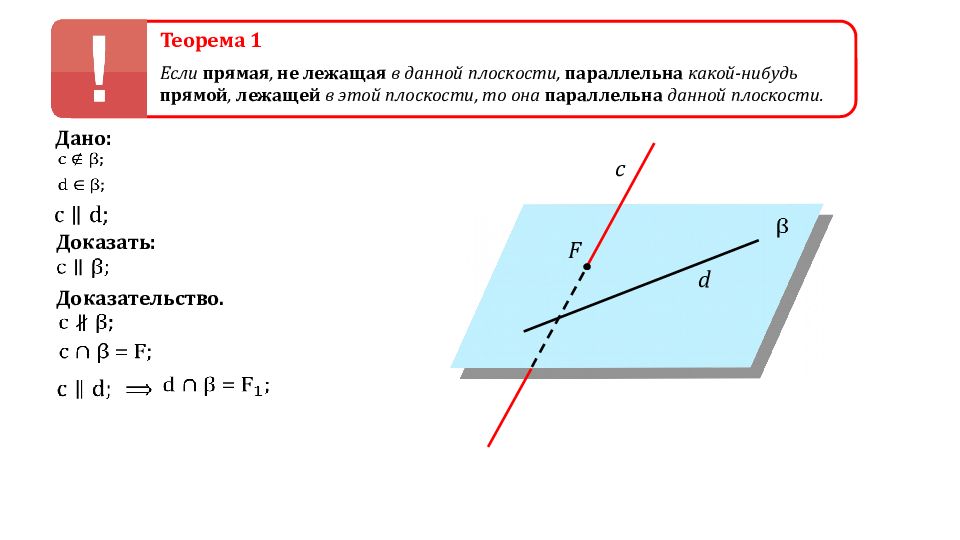
Теорема 1 Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости. d Дано: Доказать: Доказательство. c F
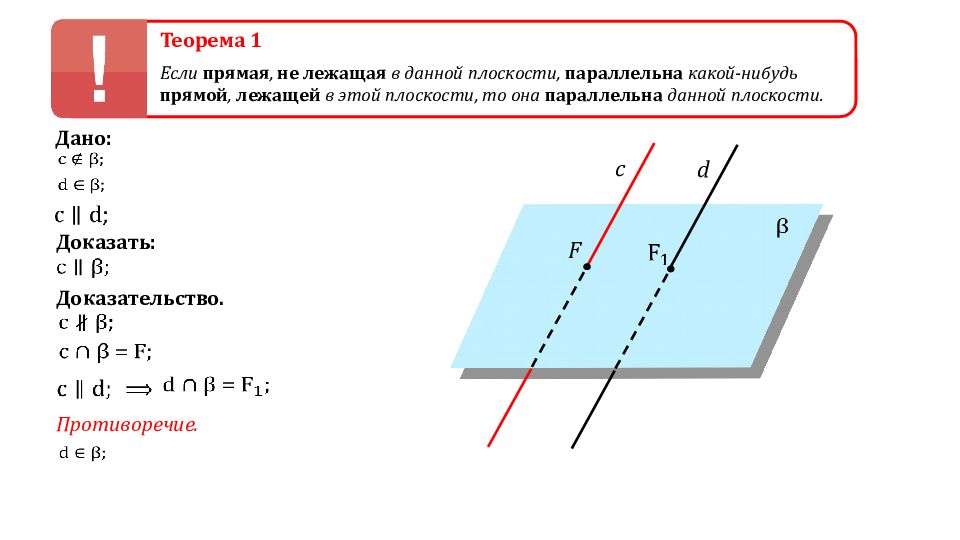
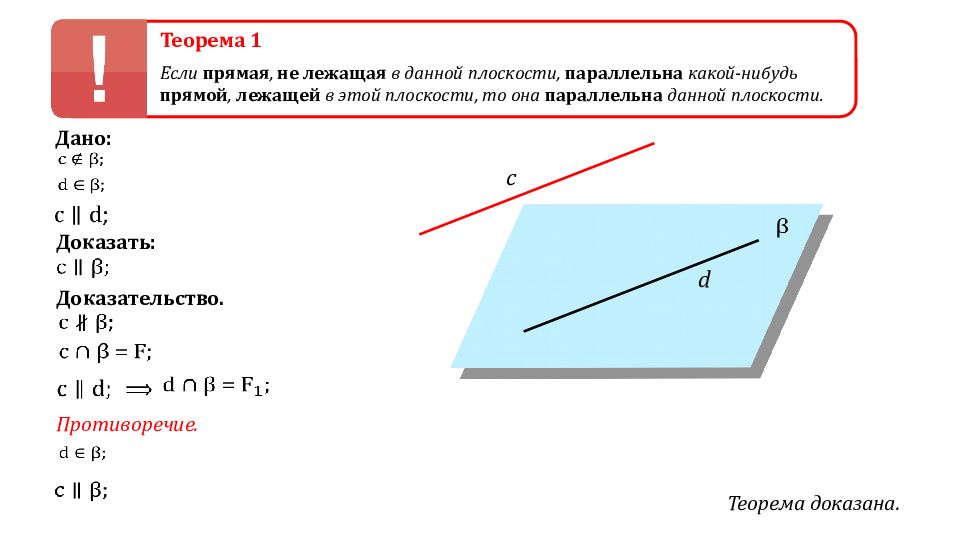
Теорема 1 Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости. d Дано: Доказать: Доказательство. c F Противоречие.
Теорема 1 Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости. Дано: Доказать: Доказательство. Противоречие. d c Теорема доказана.
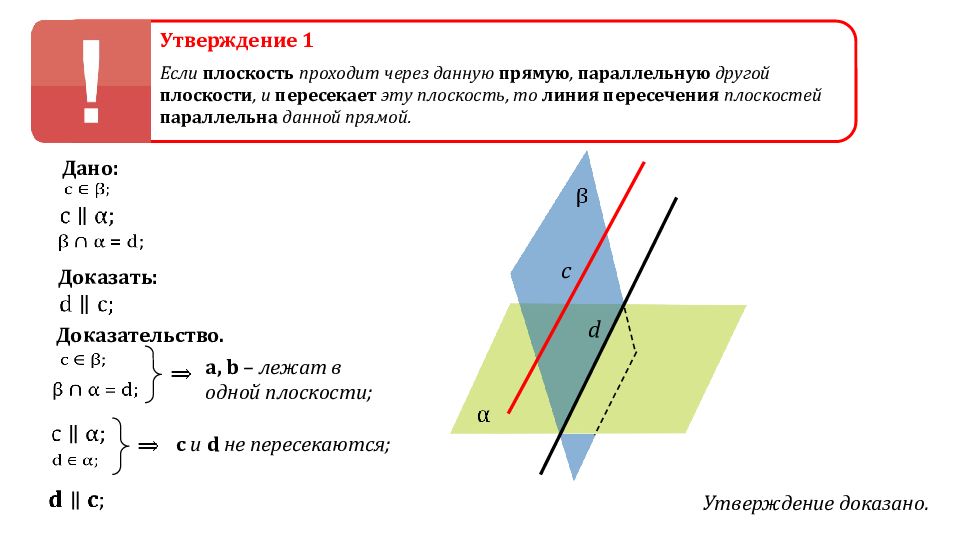
Утверждение 1 Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой. Дано: Доказать: Доказательство. a, b – лежат в одной плоскости; c и d не пересекаются; Утверждение доказано. с d
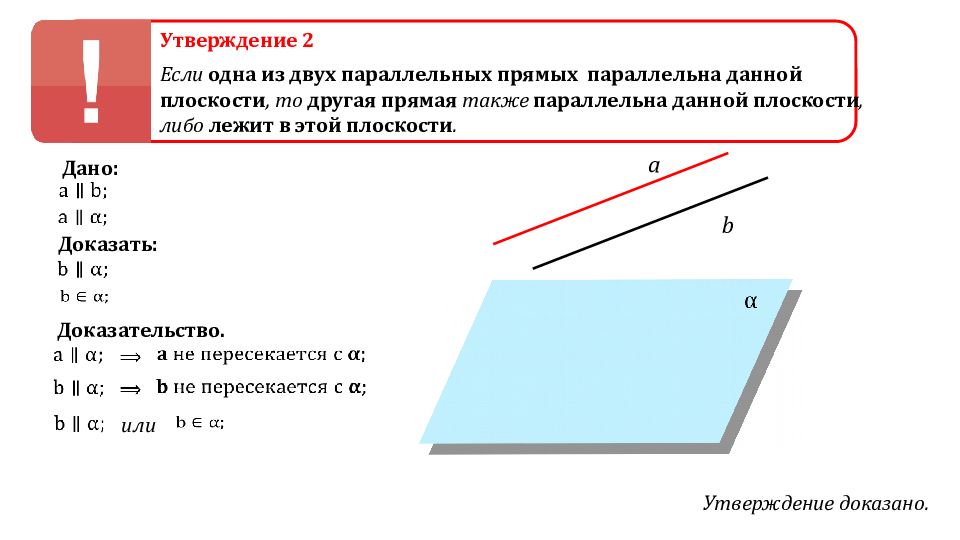
Утверждение 2 Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая также параллельна данной плоскости, либо лежит в этой плоскости. Дано: Доказать: Доказательство. Утверждение доказано. или b a
Задача 1. Дано: Найти: Решение: C – середина AB; A B C
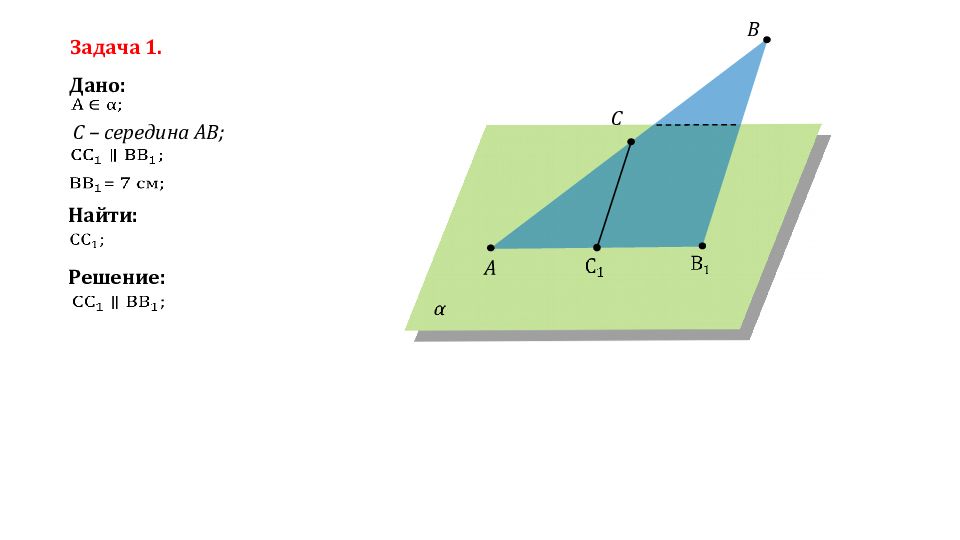
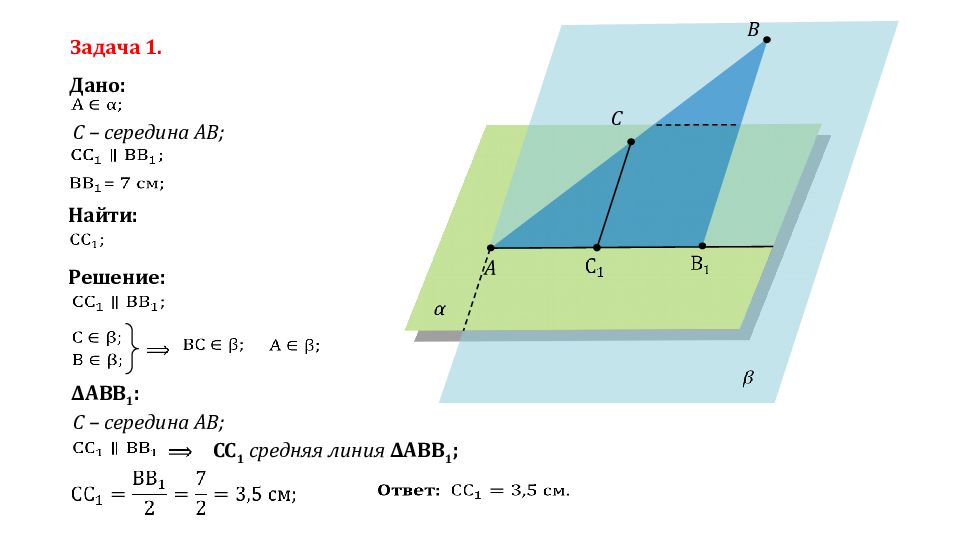
Задача 1. Дано: Найти: Решение: C – середина AB; A B C C – середина AB; Δ ABB 1 : CC 1 средняя линия Δ ABB 1 ;
Задача 2. Дано: Найти: Решение: Ответ: Нет. ABCD – трапеция ; KL – ср. линия трапеции ; Пересекают ли прямые BC и AD плоскость ? B C L K D A
