Первый слайд презентации: Перпендикулярные прямые в пространстве»
«Параллельные прямые, перпендикулярные к плоскости». «Перпендикулярность прямой и плоскости» Тема урока:
Слайд 2: Цели урока:
Ввести понятие перпендикулярных прямых в пространстве; Доказать лемму о перпендикулярности двух параллельных прямых к третьей прямой; Дать определение перпендикулярности прямой и плоскости; Доказать теоремы, в которых устанавливается связь между параллельностью прямых и их перпендикулярности к плоскости.
Слайд 3: ВСПОМНИМ ПЛАНИМЕТРИЮ
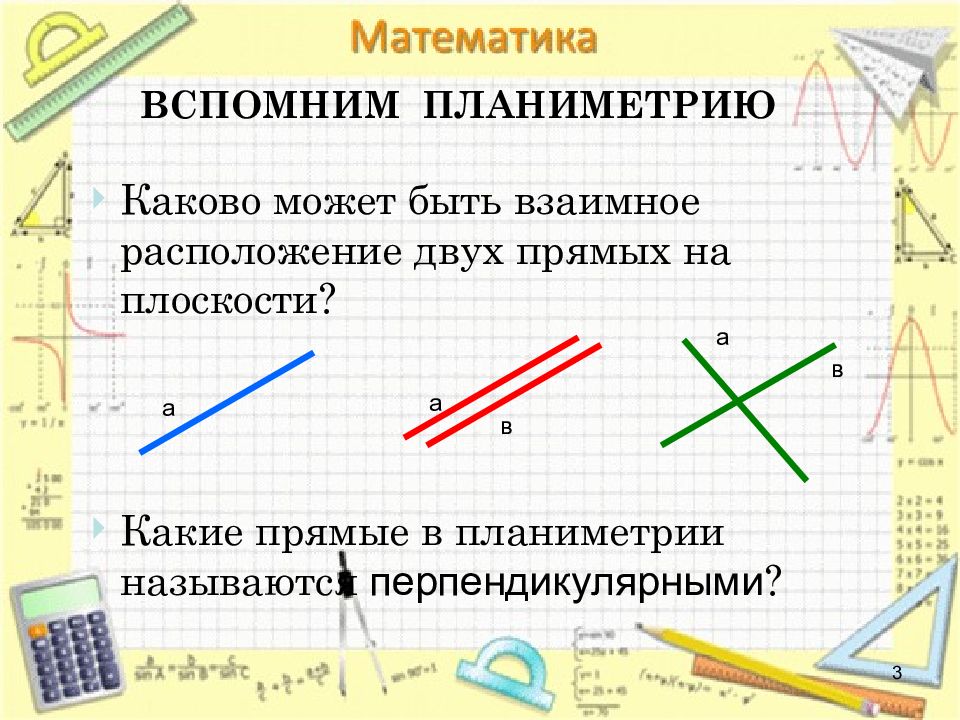
3 ВСПОМНИМ ПЛАНИМЕТРИЮ Каково может быть взаимное расположение двух прямых на плоскости? Какие прямые в планиметрии называются перпендикулярными ? а а в а в
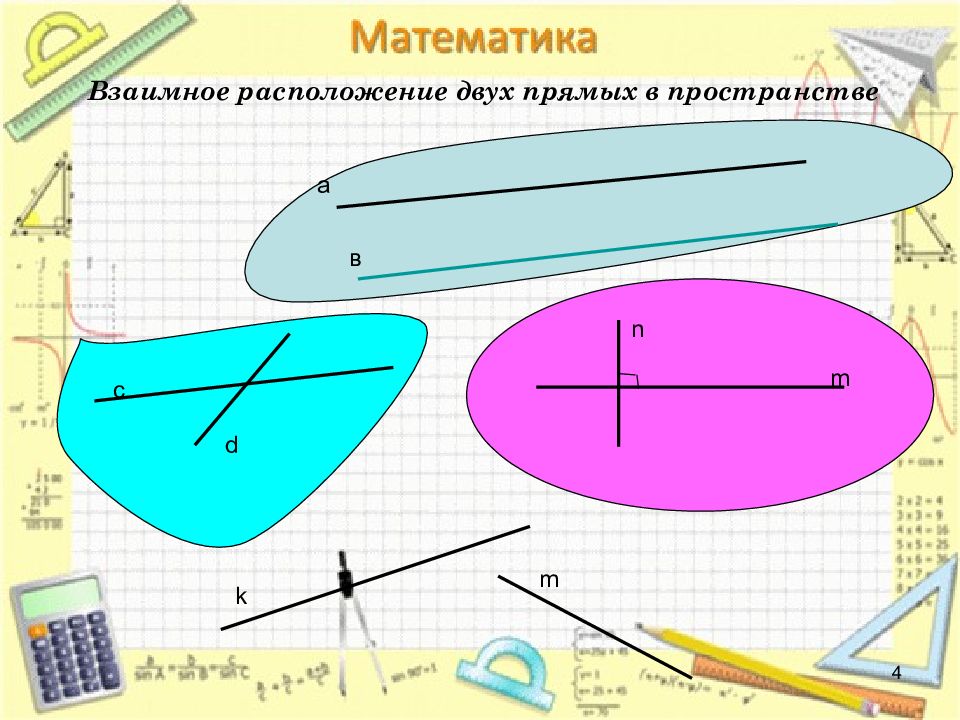
4 Взаимное расположение двух прямых в пространстве а в с d m n k m
Слайд 5
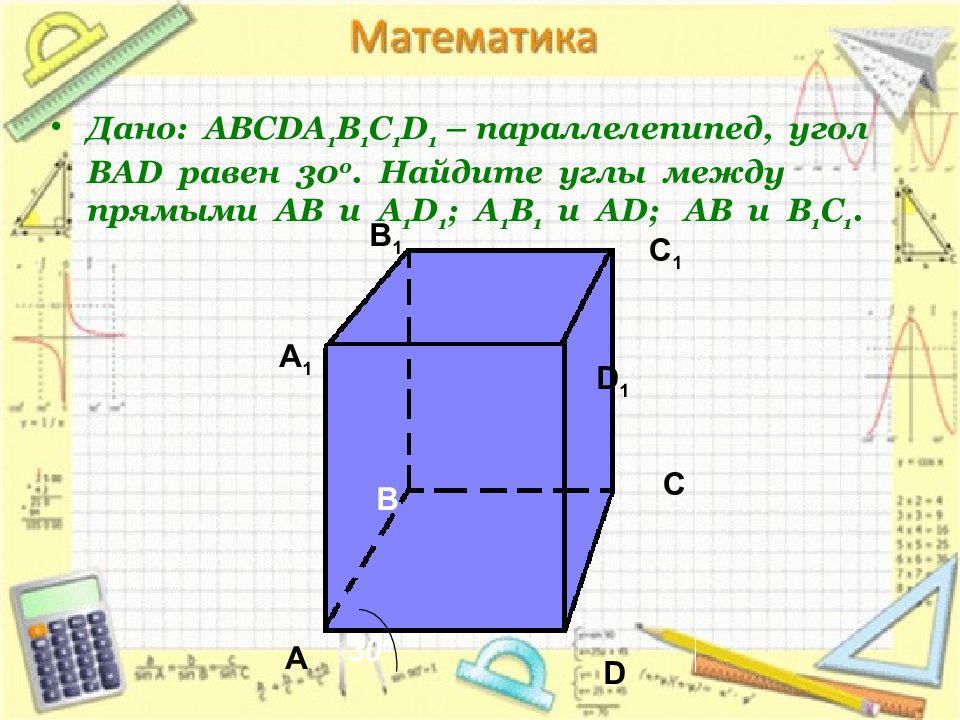
Дано: АВС DA 1 B 1 C 1 D 1 – параллелепипед, угол ВА D равен 30 0. Найдите углы между прямыми АВ и А 1 D 1 ; А 1 В 1 и А D ; АВ и В 1 С 1. А А 1 В В 1 С С 1 D D 1 30 0
Слайд 6: Модель куба
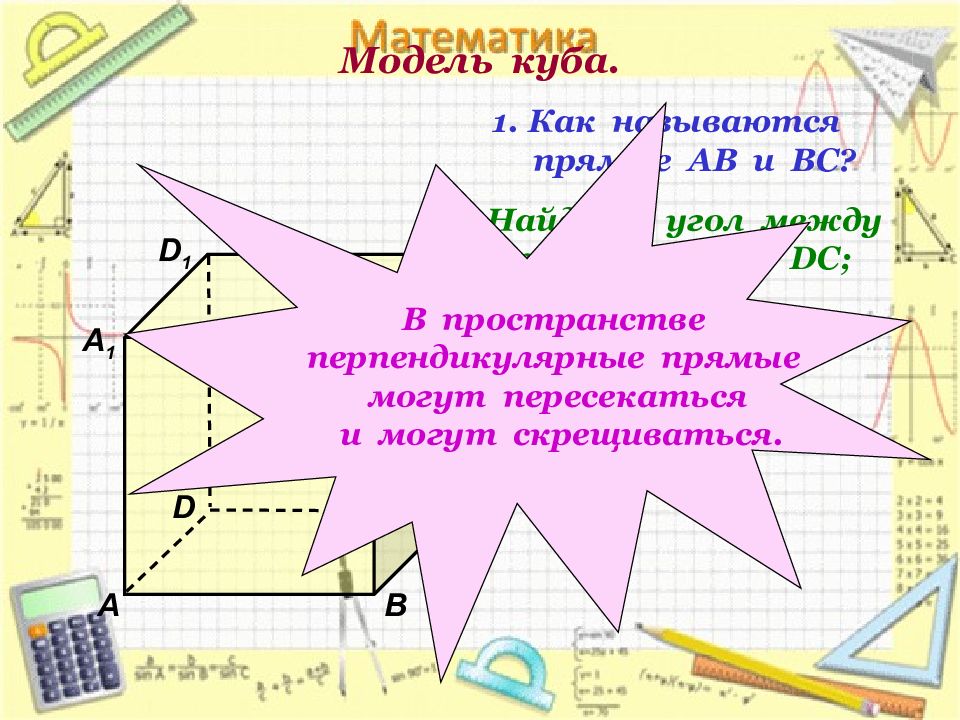
D 1 В А 1 А D С 1 С В 1 Как называются прямые АВ и ВС? Найдите угол между прямыми АА 1 и DC ; ВВ 1 и А D. В пространстве перпендикулярные прямые могут пересекаться и могут скрещиваться.
Две прямые в пространстве называются перпендикулярными ( взаимно перпендикулярными ), если угол между ними равен 90 °. Обозначается a ┴ b Перпендикулярные прямые могут пересекаться и могут быть скрещивающимися. а b c
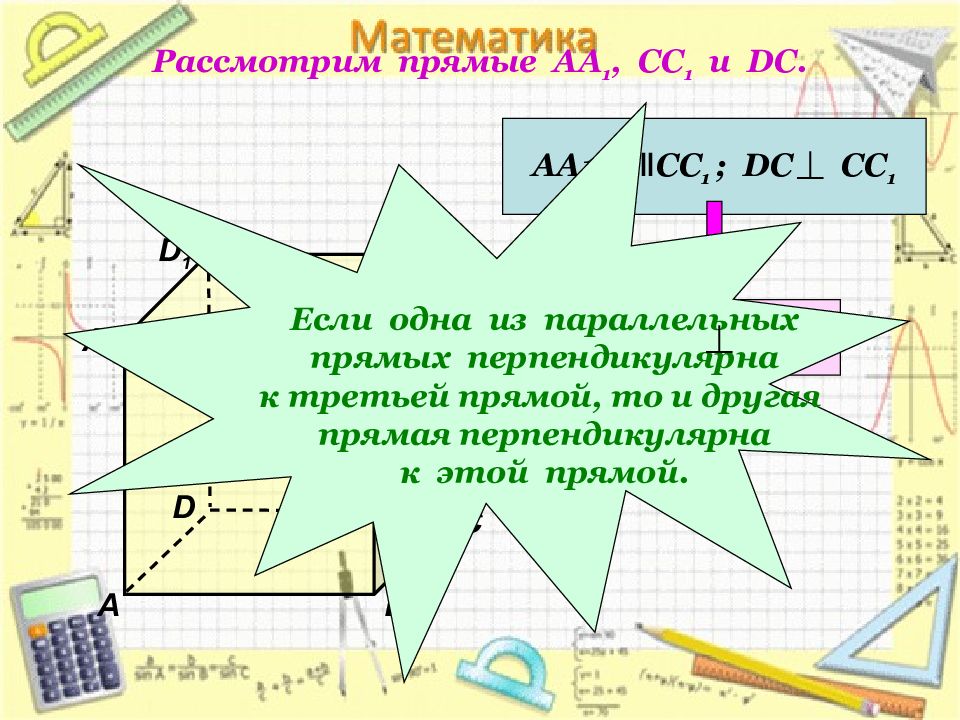
Слайд 8: Рассмотрим прямые АА 1, СС 1 и DC
D 1 В А 1 А D С 1 С В 1 АА1 ǁ СС 1 ; DC СС 1 АА 1 DC Если одна из параллельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к этой прямой.
Слайд 9: Свойства :
1. Если плоскость перпендикулярна одной из двух параллельных прямых, то она перпендикулярна другой прямой. ( a ⊥ α b и a II b = > b ⊥ α ) 2. Если две прямые перпендикулярны одной и той же плоскости, то они параллельны. (a ⊥ α и b ⊥ α => a II b) 3. Если прямая перпендикулярна одной из двух параллельных плоскостей, то она перпендикулярна и другой плоскости. ( α II β и a ⊥ α => a ⊥ β )
Слайд 10: Свойства :
4. Если две различные плоскости перпендикулярны одной и той же прямой, то эти плоскости параллельны. (a ⊥ α и a ⊥ β => a II β ) 5. Через любую точку пространства можно провести прямую, перпендикулярную данной плоскости, и притом только одну. 6. Через любую точку прямой можно провести плоскость, перпендикулярную ей и притом только одну.
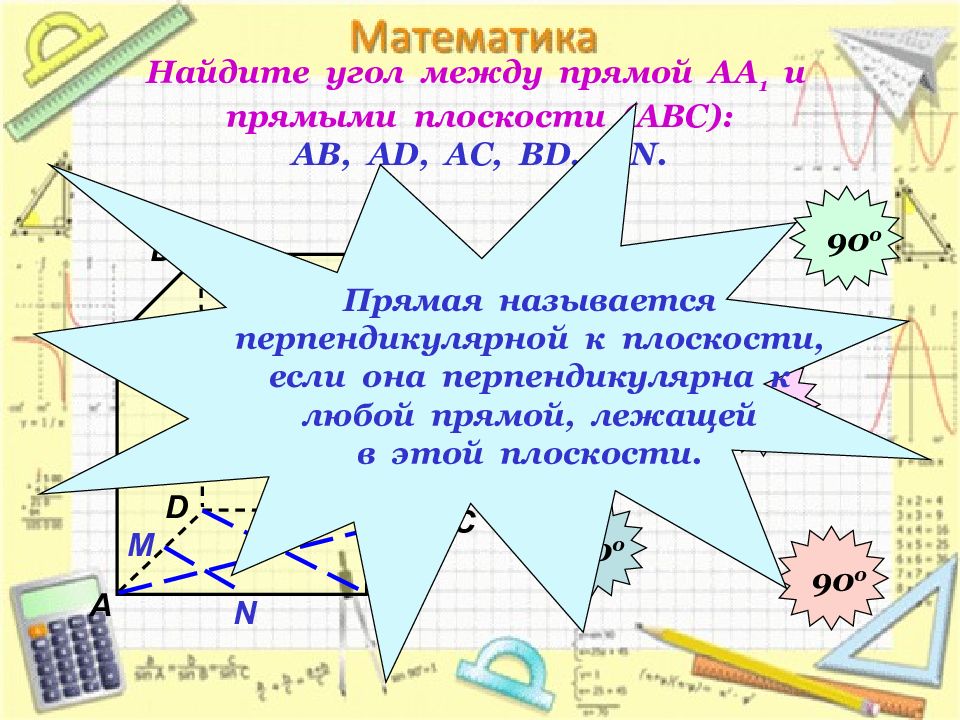
Слайд 11: Найдите угол между прямой АА 1 и прямыми плоскости (АВС): АВ, А D, АС, В D, М N
D 1 В А 1 А D С 1 С В 1 N М 90 0 90 0 90 0 90 0 90 0 Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости.
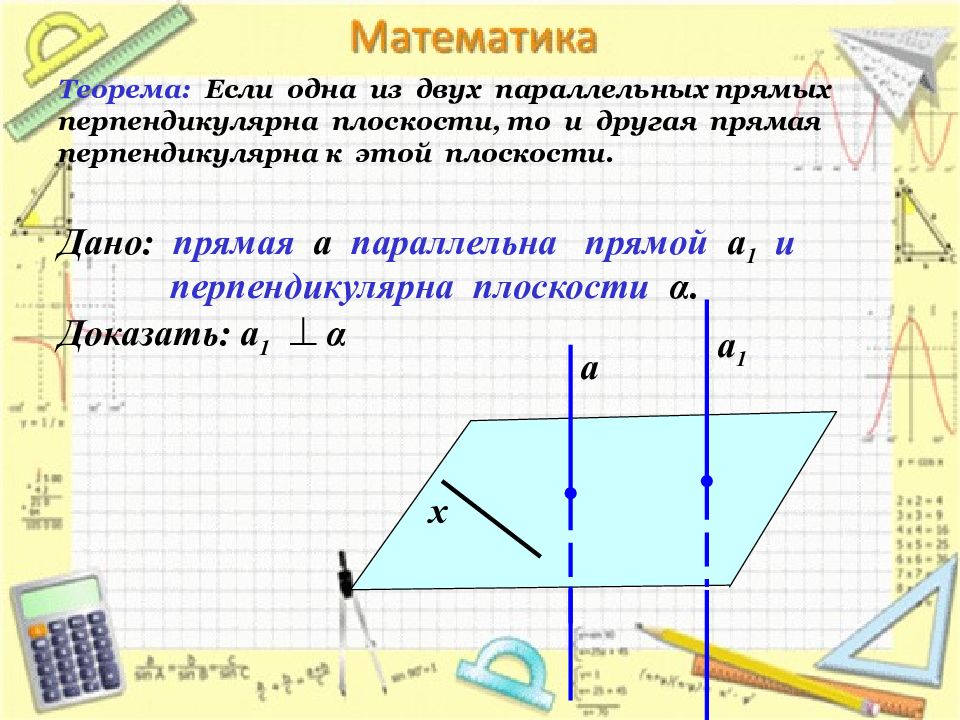
Слайд 13: Теорема: Если одна из двух параллельных прямых перпендикулярна плоскости, то и другая прямая перпендикулярна к этой плоскости
Дано: прямая а параллельна прямой а 1 и перпендикулярна плоскости α. Доказать: а 1 α а а 1 х
Слайд 14
Проведем прямую х в плоскости . Так как а, то ах. По лемме о перпендикулярности двух параллельных прямых к третьей а х. Т.о., прямая а1 перпендикулярна к любой прямой, лежащей в плоскости , т.е. а . 1 1
Слайд 15
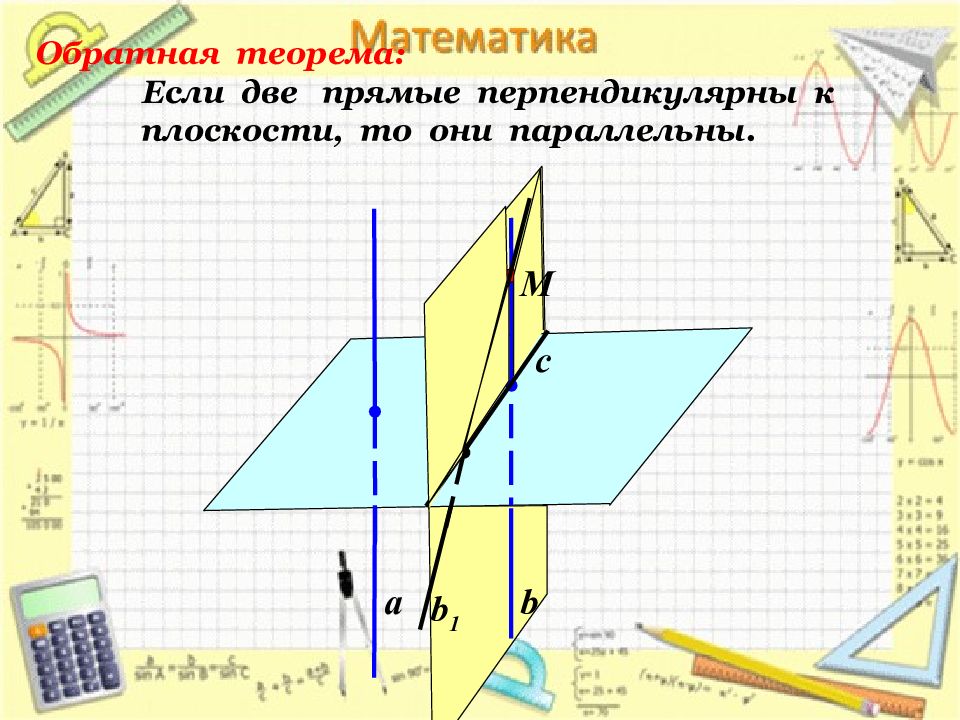
а b b 1 Обратная теорема: Если две прямые перпендикулярны к плоскости, то они параллельны. M c
Слайд 16: Признак перпендикулярности прямой и плоскости
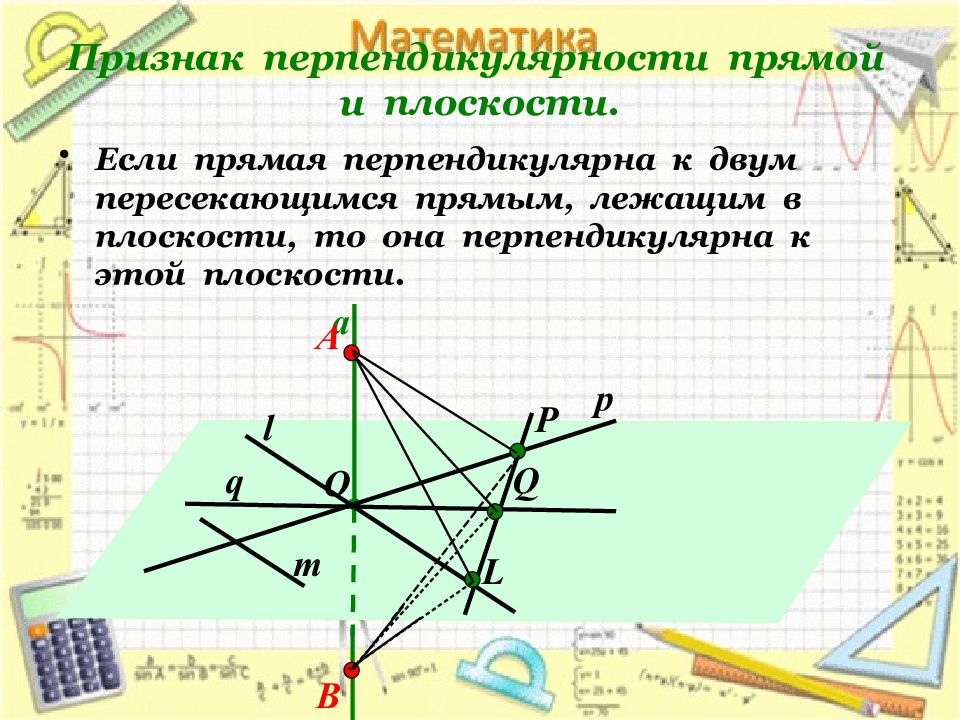
Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости. а р q O m l А B Q Р L
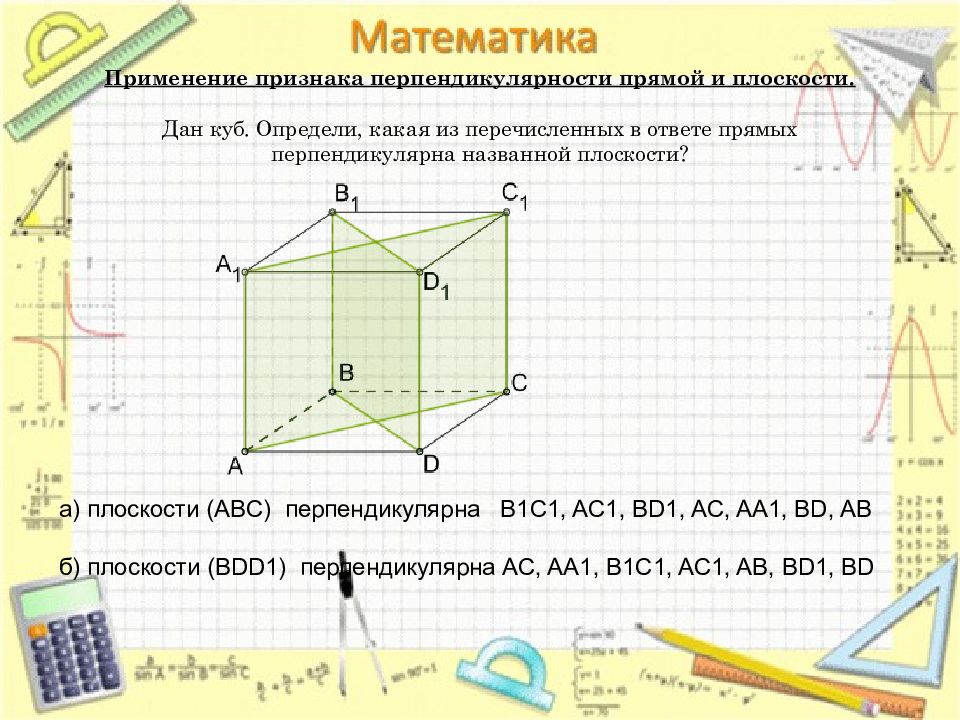
Слайд 17: Применение признака перпендикулярности прямой и плоскости. Дан куб. Определи, какая из перечисленных в ответе прямых перпендикулярна названной плоскости?
а) плоскости (ABC) перпендикулярна B1C1, AC1, BD1, AC, AA1, BD, AB б) плоскости (BDD1) перпендикулярна AC, AA1, B1C1, AC1, AB, BD1, BD
Слайд 18: Две прямые, перпендикулярные одной плоскости
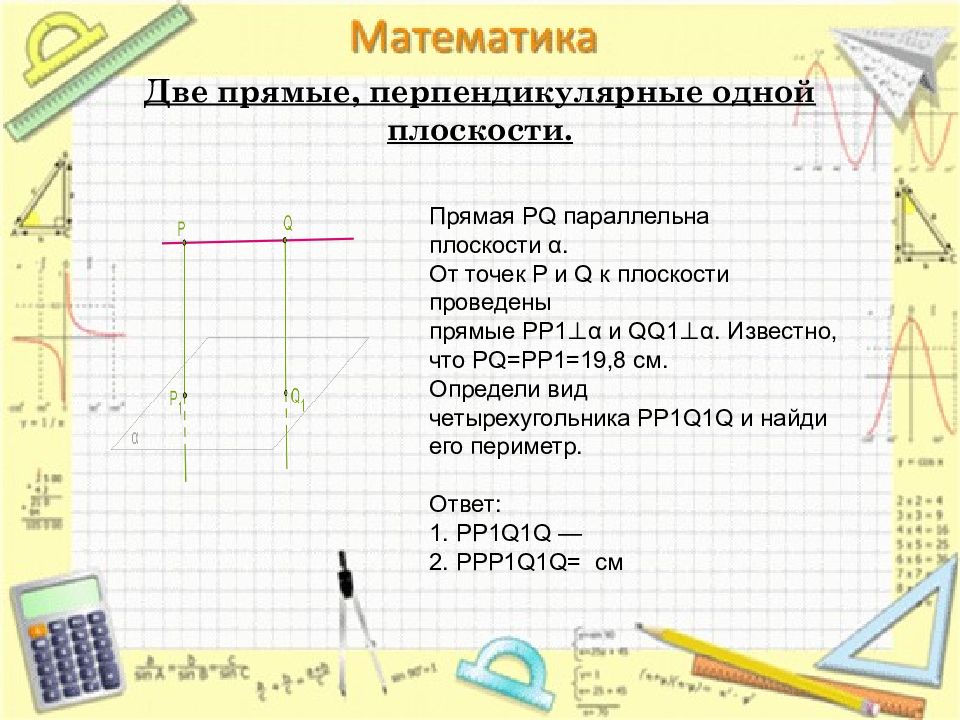
Прямая PQ параллельна плоскости α. От точек P и Q к плоскости проведены прямые PP1⊥α и QQ1⊥α. Известно, что PQ=PP1=19,8 см. Определи вид четырехугольника PP1Q1Q и найди его периметр. Ответ: 1. PP1Q1Q — 2. PPP1Q1Q= см
Слайд 19: Перпендикулярность прямой к плоскости
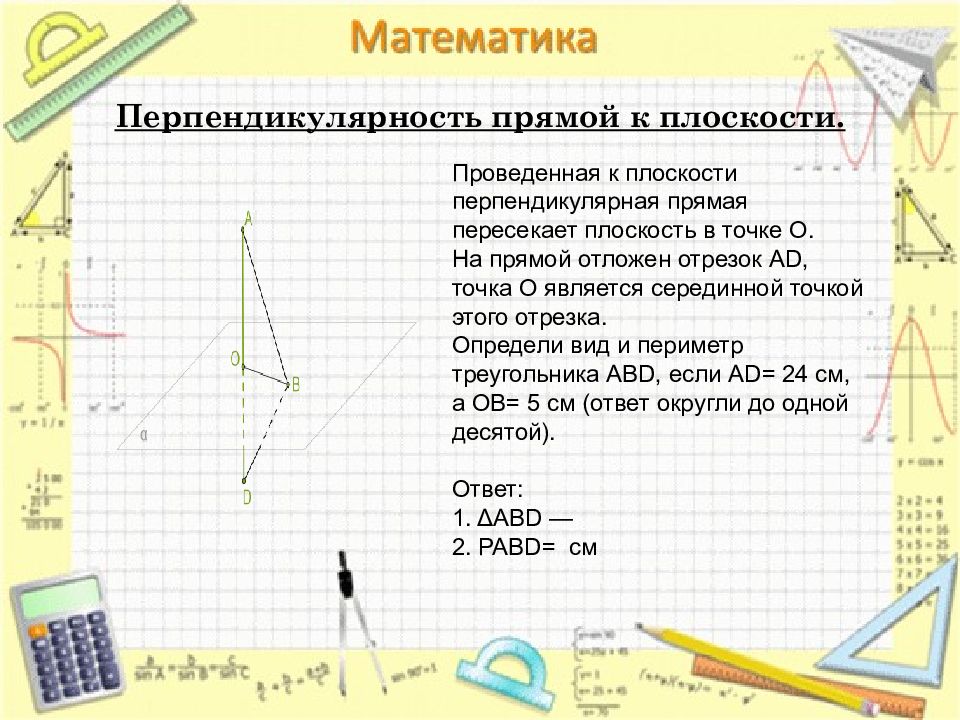
Проведенная к плоскости перпендикулярная прямая пересекает плоскость в точке O. На прямой отложен отрезок AD, точка O является серединной точкой этого отрезка. Определи вид и периметр треугольника ABD, если AD= 24 см, а OB= 5 см (ответ округли до одной десятой). Ответ: 1. ΔABD — 2. PABD= см
Слайд 20: Прямые, перпендикулярные к плоскости
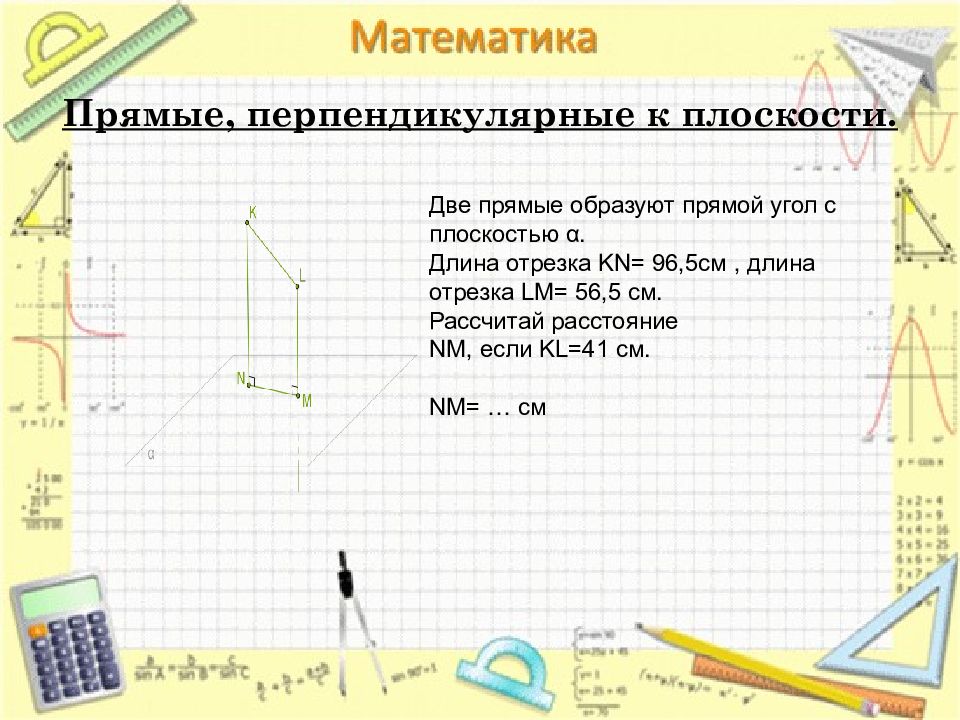
Две прямые образуют прямой угол с плоскостью α. Длина отрезка KN= 96,5cм, длина отрезка LM= 56,5 см. Рассчитай расстояние NM, если KL=41 см. NM= … см
Слайд 21: Перпендикуляр к плоскости квадрата
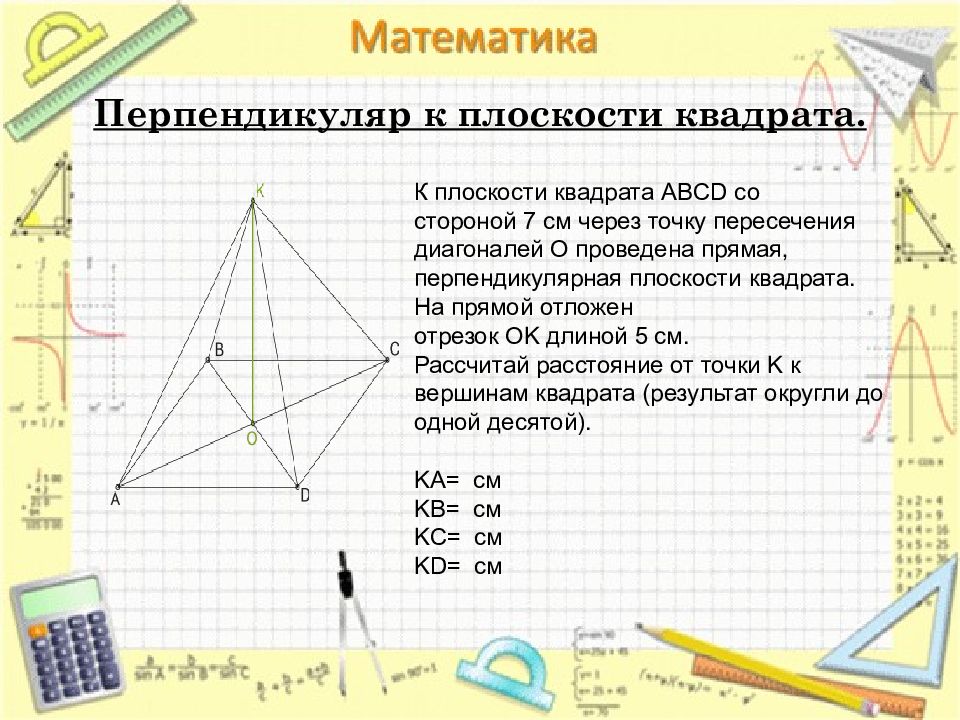
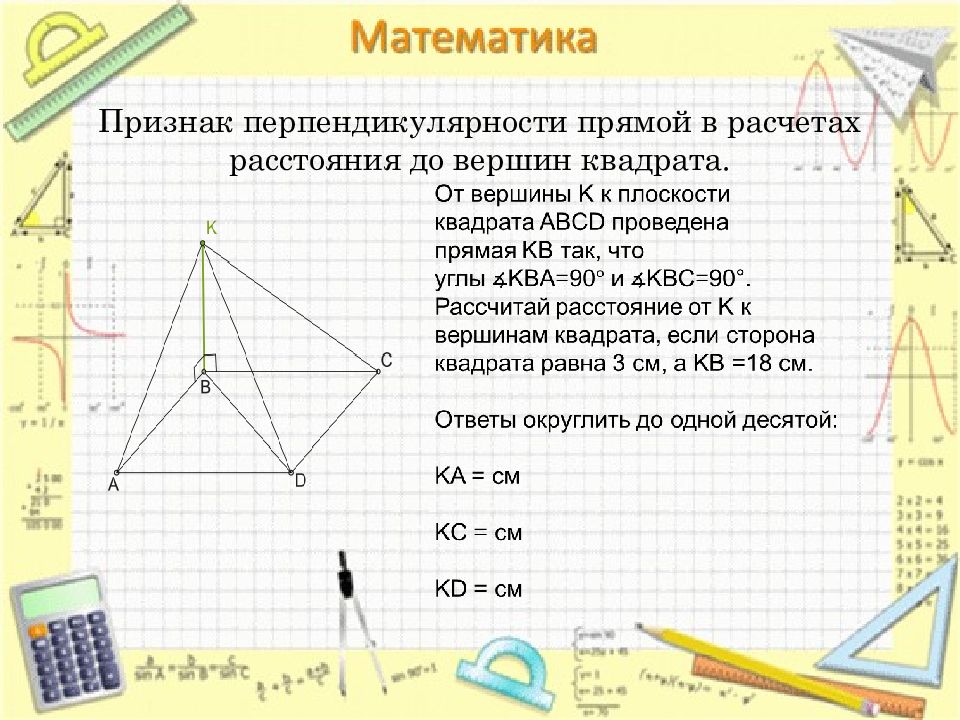
К плоскости квадрата ABCD со стороной 7 см через точку пересечения диагоналей O проведена прямая, перпендикулярная плоскости квадрата. На прямой отложен отрезок OK длиной 5 см. Рассчитай расстояние от точки K к вершинам квадрата (результат округли до одной десятой). KA= см KB= см KC= см KD= см
Слайд 22: Доказательство перпендикулярности скрещивающихся прямых
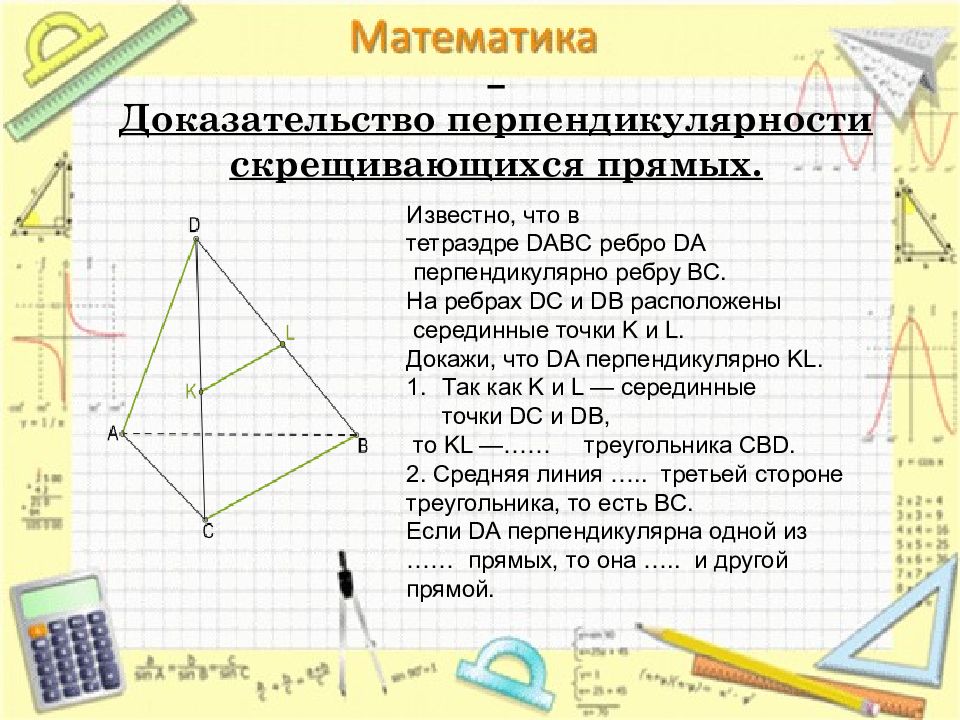
Известно, что в тетраэдре DABC ребро DA перпендикулярно ребру BC. На ребрах DC и DB расположены серединные точки K и L. Докажи, что DA перпендикулярно KL. Так как K и L — серединные точки DC и DB, то KL —…… треугольника CBD. 2. Средняя линия ….. третьей стороне треугольника, то есть BC. Если DA перпендикулярна одной из …… прямых, то она ….. и другой прямой.
Слайд 23: Признак перпендикулярности прямой к плоскости
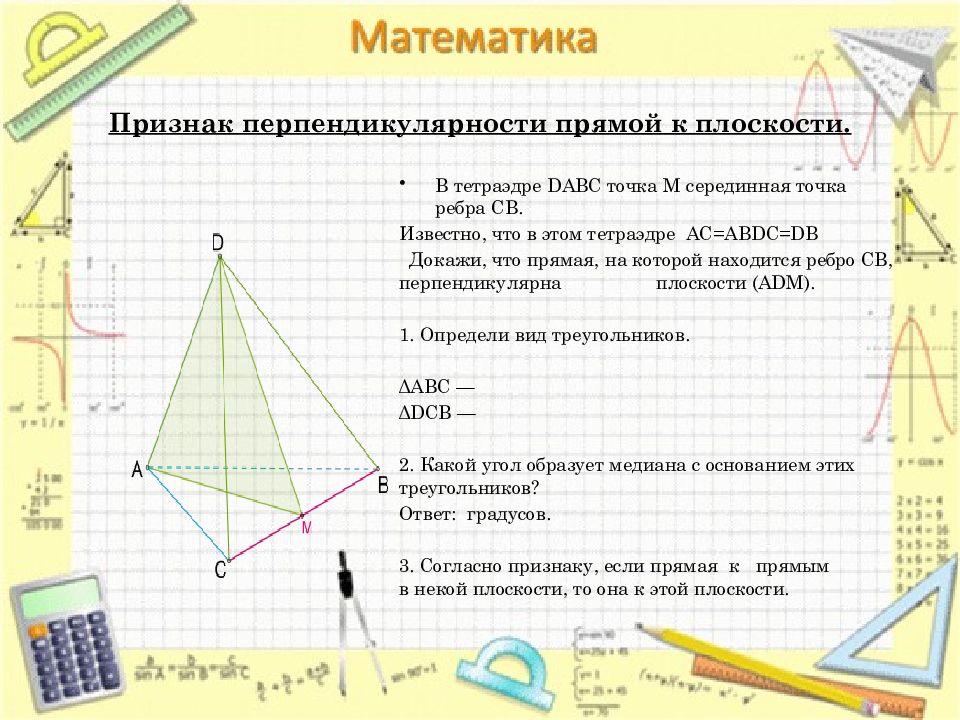
В тетраэдре DABC точка M серединная точка ребра CB. Известно, что в этом тетраэдре AC=ABDC=DB Докажи, что прямая, на которой находится ребро CB, перпендикулярна плоскости (ADM). 1. Определи вид треугольников. ΔABC — ΔDCB — 2. Какой угол образует медиана с основанием этих треугольников? Ответ: градусов. 3. Согласно признаку, если прямая к прямым в некой плоскости, то она к этой плоскости.
Слайд 24: Свойство прямой перпендикулярной к плоскости
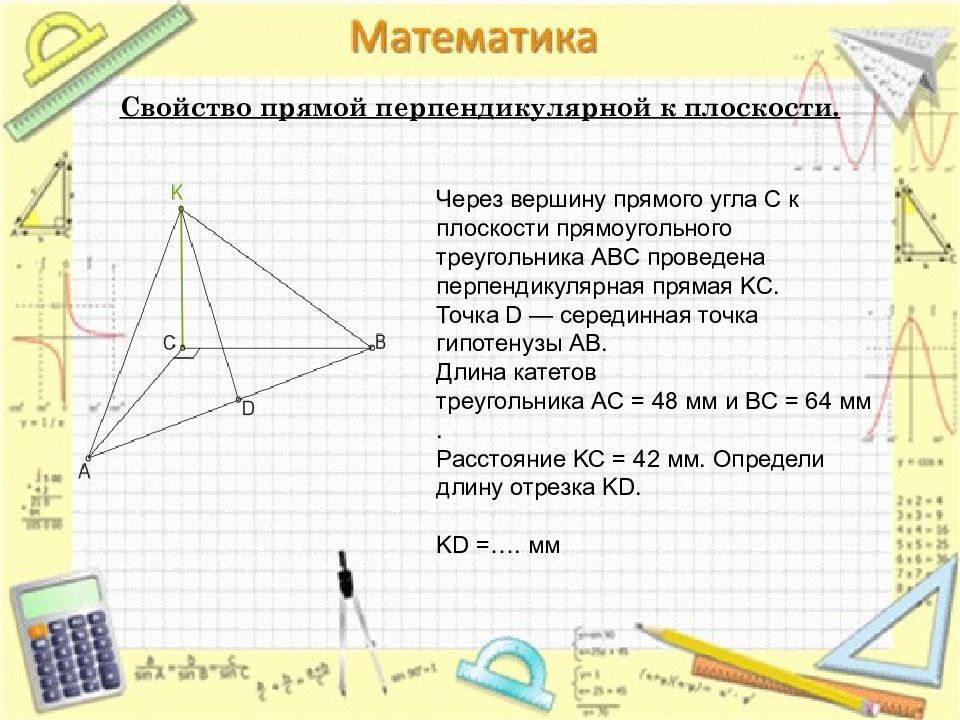
Через вершину прямого угла C к плоскости прямоугольного треугольника ABC проведена перпендикулярная прямая KC. Точка D — серединная точка гипотенузы AB. Длина катетов треугольника AC = 48 мм и BC = 64 мм. Расстояние KC = 42 мм. Определи длину отрезка KD. KD =…. мм
Слайд 25: (сложное) Доказательство от противного
Прямая d перпендикулярна плоскости α и прямой m, которая не лежит в плоскости α. Докажи, что прямая m параллельна плоскости α. 1. Согласно данной информации, если прямая не лежит в плоскости, она может или быть …плоскости, или … плоскость. 2. Допустим, что прямая m не ….., а …..плоскость α. 3. Если прямая d по данной информации перпендикулярна плоскости α, то она …… каждой прямой в этой плоскости, в том числе и прямой, которая проведена через точки, в которых плоскость пересекает прямые d и m. 4. Мы имеем ситуацию, когда через одну точку к прямой d проведены две …… прямые. 5. Это противоречие, из чего следует, что прямая m….. плоскости α, что и требовалось доказать.