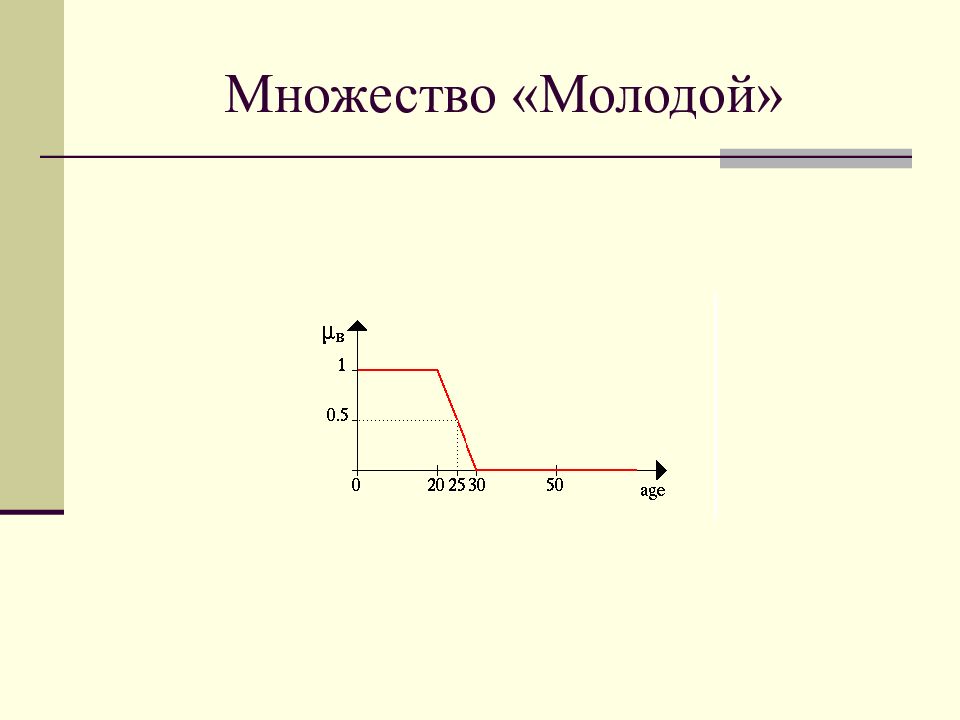
Слайд 2
Лютфи Аскер Заде (англ. Lotfi Asker Zadeh, р. 4 февраля 1921) — математик, основатель теории нечётких множеств и нечёткой логики. Родился в Баку, с 1932 года жил в Иране, учился в Alborz High School и Тегеранском университете; с 1944 в Соединенных Штатах; с 1959 работает в Калифорнийском университете (Беркли). В 1965 опубликовал основополагающую работу по теории нечётких множеств, в которой изложил математический аппарат теории нечётких множеств; в 1973 предложил теорию нечёткой логики; позднее — теорию мягких вычислений (soft computing); а также — теорию вербальных вычислений и представлений (computing with words and perceptions).
Пусть Е есть множество, счетное или нет, и x — элемент Е. Тогда нечетким подмножеством А множества Е называется множество упорядоченных пар {( x | A ( x ))}, x Е, где A ( x ) — степень принадлежности x в А. Таким образом, если A ( x ) принимает свои значения во множестве М значений функции принадлежности или, короче, во множестве принадлежностей, то можно сказать, что x принимает значение в М посредством функции A ( x ). Эта функция также называется функцией принадлежности. (Определение Л. Заде)
Слайд 4: Определение А. Кофмана
Пусть Е есть множество, счетное или нет, и x — элемент Е. Тогда нечеткое подмножество А множества Е определяется как множество упорядоченных пар {( x | A ( x ))}, x Е, где A ( x ) — характеристическая функция принадлежности x в А, принимающая свои значения во вполне упорядоченном множестве М, которая указывает степень или уровень принадлежности элемента x подмножеству А. Множество М будет называться множеством принадлежностей.
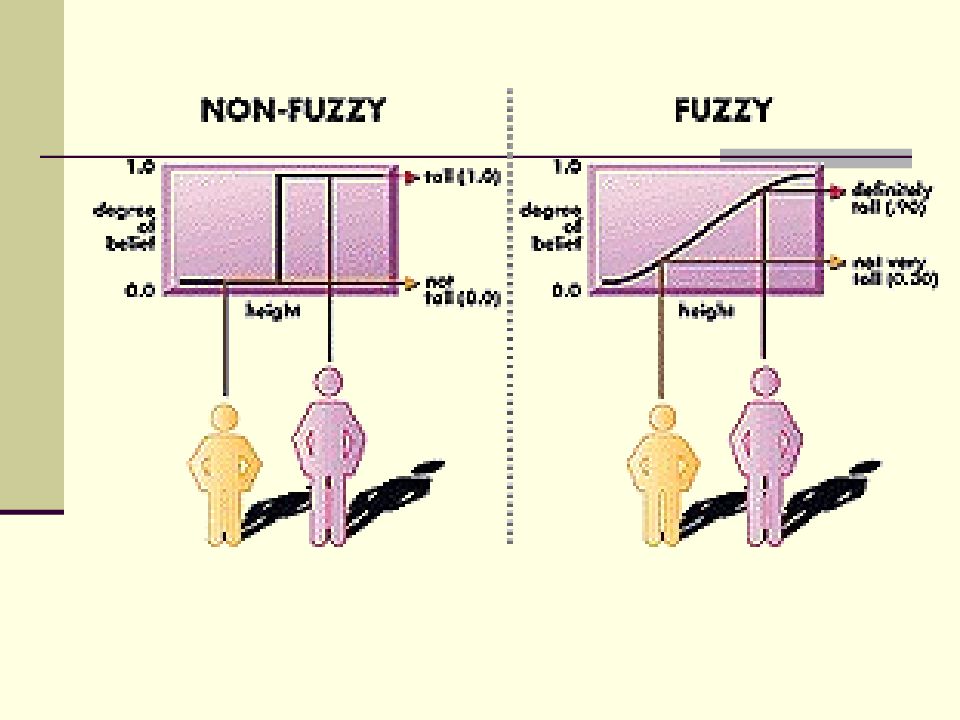
Слайд 6: Что означает степень принадлежности?
В работе Заде «Fuzzy sets» предполагается, что функция принадлежности — это некоторое «невероятностное субъективное измерение неточности», и что она отлична от плотности вероятности и от функции распределения вероятности. В работе Заде «Понятие лингвистической переменной и его применение к принятию приближенных решений» под значением функции принадлежности µ А ( u ) нечеткого множества А для любого u U понимается вероятность того, что ЛПР отнесет элемент u к множеству А. В случае, когда А – некоторое понятие естественного языка, а U – множество объектов, обозначаемых этим понятием А, µ А ( u ) – есть вероятность того, что лицо, принимающее решение, использует А в качестве имени объекта. Такая интерпретация функции принадлежности называется вероятностной и не исключает существование других интерпретаций. Однако − элемент u, как следует из определения, уже предъявлен ЛПР, а последний и решает задачу отнесения элемента к нечеткому множеству А ; − в приведенной интерпретации µ А ( u ) не является ни функцией распределения вероятности, ни плотностью распределения вероятности
Слайд 7: Что означает степень принадлежности?
степень соответствия понятию А, вероятность, возможность, полезность, истинность, правдоподобность, значение функции и др.
Слайд 8: Методы построения функции принадлежности
частотный ( вероятностная интерпретация) метод парных соотношений: есть n экспертов, каждый определяет парные соотношения, из них определяется экспертная оценка степени принадлежности, оценки усредняются по экспертам на основе стандартного набора графиков, выбранный график ЛПР корректирует
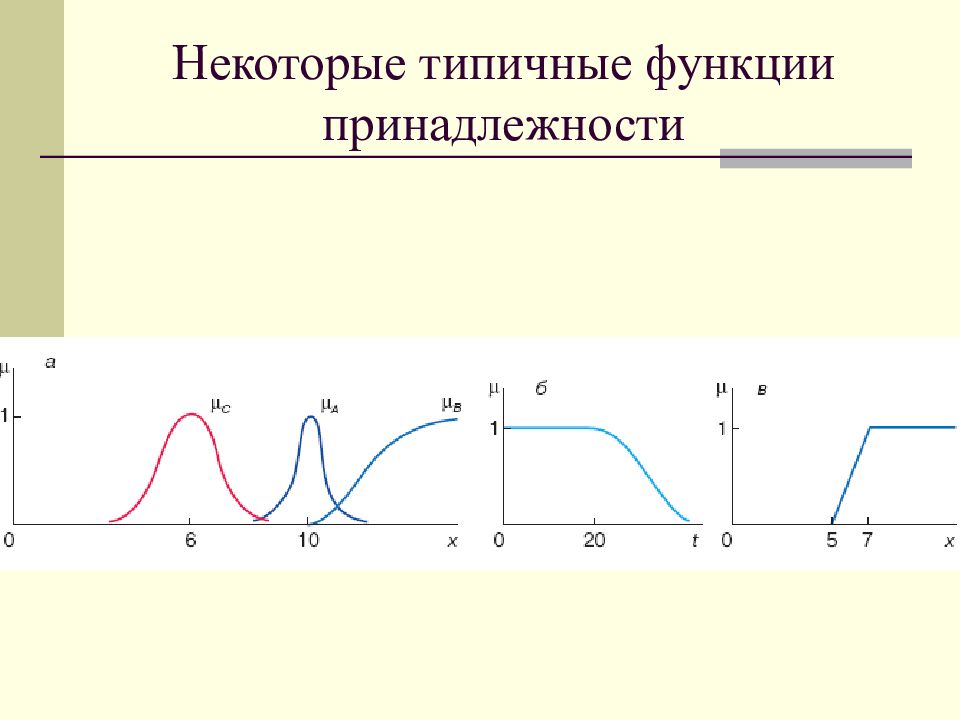
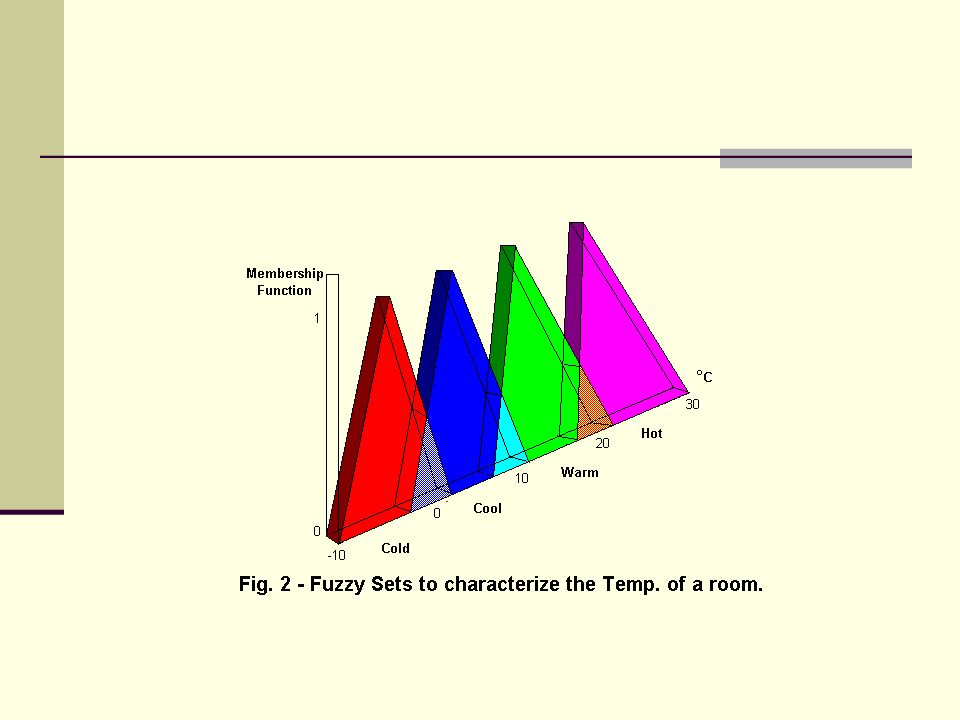
Слайд 9: Наиболее распространенные параметрические функции принадлежности
Треугольные m ( x ) = 0, при x <= a ; m ( x ) = ( x – a )/( b – a ), при a < x <= b ; m ( x ) = ( c – x )/( c – b ), при b < x <= c ; m ( x ) = 0, при с < x. Трапециевидные m ( x ) = 0, при x < a ; m ( x ) = ( x – a )/( b – a ), при a < x <= b ; m ( x )= 1, при b < x <= c ; m ( x ) = ( d – x )/( d – c ), при c < x <= d ; m ( x ) = 0, при d < x.
Слайд 10
Гауссовские функции принадлежности задаются двумя параметрами ( c, s ): m ( x ) = exp( 0.5( x c )^2/ s ^2). Колоколообразные функции принадлежности задаются параметрами ( a, b, c ): m ( x ) = 1/(1+(( x c )/ a )^(2 b ))
Слайд 15
Нечеткое множество А называется пустым, если A ( x ) = 0, x Е Носителем нечеткого множества А называется обычное подмножество таких точек Е, для которых величина A ( x ) положительна. Носитель обозначается S ( A ) или Supp A : S ( A ) = { x | x Е, A ( x ) > 0 } Высотой h ( A ) нечеткого множества А называется величина h ( A ) = sup A ( x ) по всем x Е Нечеткое множество А называется нормальным, если его высота равна единице. В противном случае нечеткое множество А субнормально. Элементы множества Е, для которых степень принадлежности A ( x ) = 0.5 называются точками перехода нечеткого множества
Слайд 16: Логические операции над нечеткими множествами
Операция включения ( A B ). Пусть A и B — нечеткие подмножества. Будем говорить, что A содержится в B, и обозначать A B, если x Е, A ( x ) B ( x ) Равенство. A и B равны ( A = B ), если x Е, A ( x ) = B ( x )
Слайд 17: Сечения нечеткого множества
Множеством -уровня нечеткого множества А является обычное множество А всех таких элементов универсального множества Е, степень принадлежности которых нечеткому множеству А больше или равна : A = { x | x Е, A ( x ) }. Множество - уровня называют иногда сечением нечеткого множества А. Причем, если A ( x ) , то говорят о сильном сечении, если A ( x ) > , то о слабом сечении. Нечеткое множество А можно разложить по его множествам уровня следующим образом: где A — произведение числа на множество A . Знак — знак объединения множеств A по . Сечения нечеткого множества
Слайд 18: Операции над нечеткими множествами
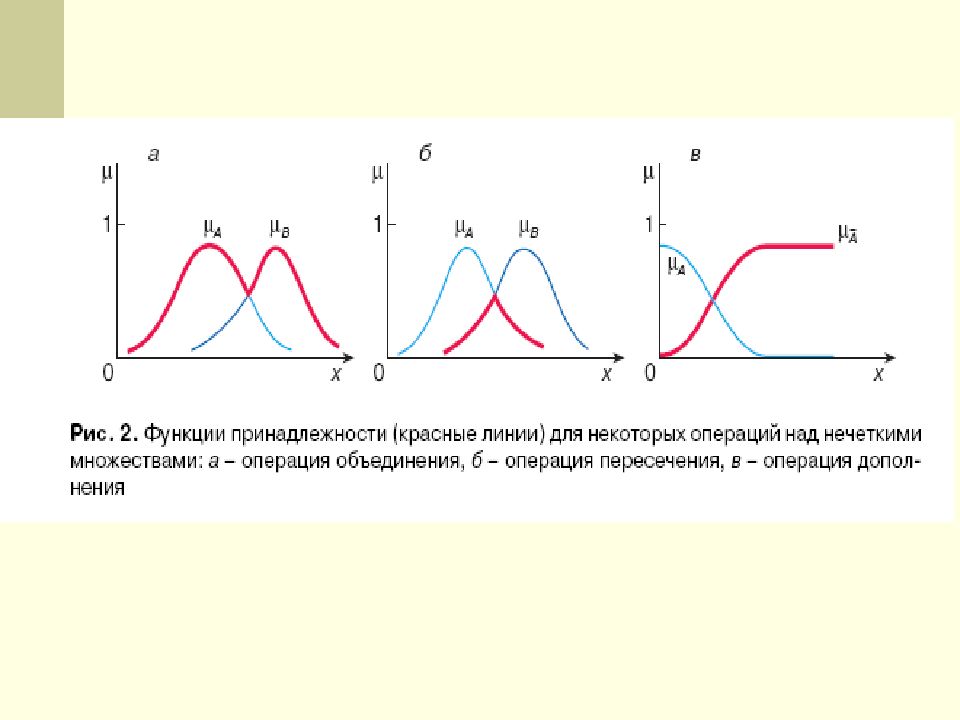
Функция принадлежности для объединения двух нечетких множеств А и B с функциями принадлежности определена как максимум из двух индивидуальных функций принадлежности. Это называется критерием максимума. Объединением нечетких множеств А и В в Е называют наименьшее нечеткое подмножество A Y В, включающее как А, так и В, с функцией принадлежности вида: A Y B ( x ) = max( A ( x ), B ( x )), x E
Слайд 19: Пересечение
Функция принадлежности пересечения двух нечетких множеств А и B с функциями принадлежности и определена как минимум из двух индивидуальных функций принадлежности. Это называется критерием минимума. Пересечением нечетких множеств А и В в Е называют наибольшее нечеткое подмножество А I В, содержащееся одновременно в А и В, с функцией принадлежности вида: A I B ( x ) = min( A ( x ), B ( x )), x E
Слайд 20: Дополнение
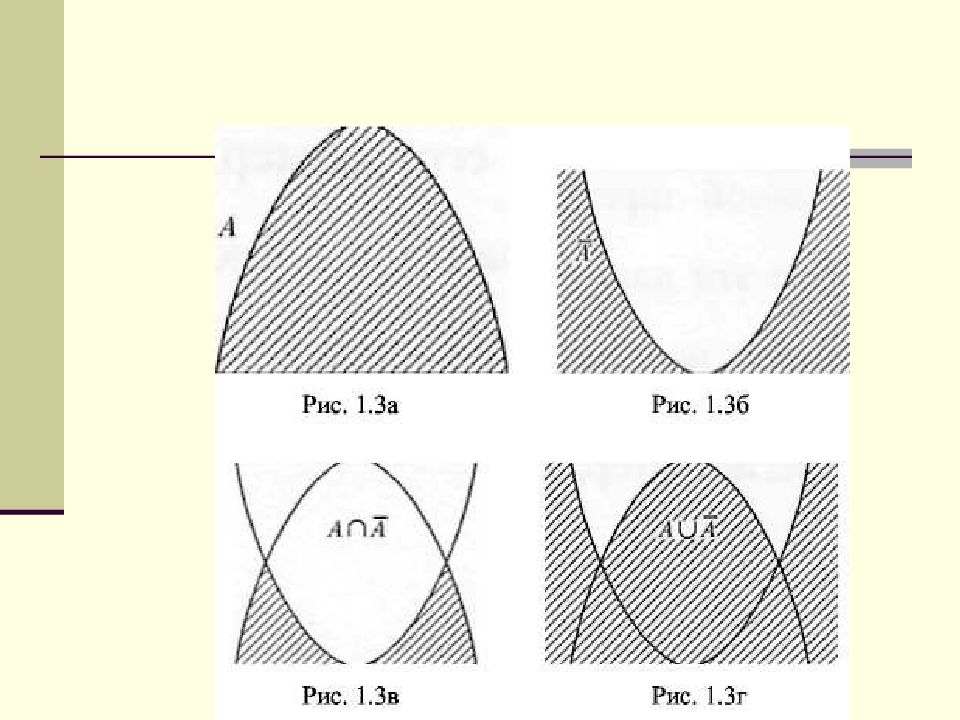
Функция принадлежности дополнения нечеткого множества А с функцией принадлежности определена как отрицание данной функции членства. Это называется критерием отрицания Дополнением нечеткого множества А называют нечеткое множество A с функцией принадлежности: A ( x ) = 1 A ( x ), x E
Слайд 21
Разность нечетких множеств А и В определяется по-разному, введением двух независимых операций или A B ( x ) = min( A ( x ), 1 B ( x )), x E Дизъюнктивная сумма А В нечетких множеств А и В определяется как A B ( x ) = max[ min( A ( x ), 1 B ( x ) ), min( B ( x ), 1 A ( x ))] x E
Слайд 26: Алгебраические операции
Алгебраическое произведение А и В обозначается определяется функцией принадлежности вида A B ( x ) = A ( x ) B ( x ), x E Алгебраическая сумма этих множеств обозначается А+В и определяется функцией принадлежности A+ B ( x ) = A ( x ) + B ( x ) — A ( x ) B ( x ), x E Степенью нечеткого множества A называется нечеткое множество A α с функцией принадлежности µ A α ( x ) = µ α A ( x ), x E, α>0.
Слайд 27: Операции концентрирования, растяжения и контрастной интенсификации
При α = 2 получаем операцию концентрирование (уплотнение) (CON): CON(A) = A 2 В результате применения этой операции к множеству А снижается степень нечеткости описания, причем для элементов с высокой степенью принадлежности это уменьшение относительно мало, а для элементов с малой степенью принадлежности относительно велико. При α = 0.5 получаем операцию растяжения (DIL): DIL(A) = A 0.5 Эта операция увеличивает степень нечеткости исходного нечеткого множества. Операция контрастной интенсификации (INT) определяется с помощью функции принадлежности следующим образом: Умножение на число.
Слайд 28
Декартово ( прямое ) произведение. Пусть А 1, А 2, … А n нечеткие подмножества универсальных множеств U 1, U 2, … U n соответственно. Декартово произведение А = А 1 × А 2 ×…× А n является нечетким подмножеством декартового произведения U = U 1 × U 2 ×…× U n c функцией принадлежности вида: A ( x ) = min( A1 ( x 1 ), …, A n ( x n )), x = ( x 1, …, x n ) U
Слайд 29: Расстояние между нечеткими множествами
неотрицательность; симметричность; транзитивность Расстояние Хэмминга Относительное расстояние Хэмминга:
Слайд 30
Евклидово или квадратичное расстояние Относительное евклидово расстояние
Слайд 31: Индексы нечеткости
Обычное подмножество, ближайшее к нечеткому Линейный индекс нечеткости Квадратичный индекс нечеткости
Слайд 32: Нечеткие отношения
Нечеткие отношения играют фундаментальную роль в теории нечетких систем. Аппарат теории нечетких отношений используется при построении теории нечетких автоматов, при моделировании структуры сложных систем, при анализе процессов принятия решений Обычное неразмытое n -арное отношение R определяется как подмножество декартова произведения множеств Нечеткое отношение можно задать с помощью его функции принадлежности
Слайд 33: Бинарные нечеткие отношения
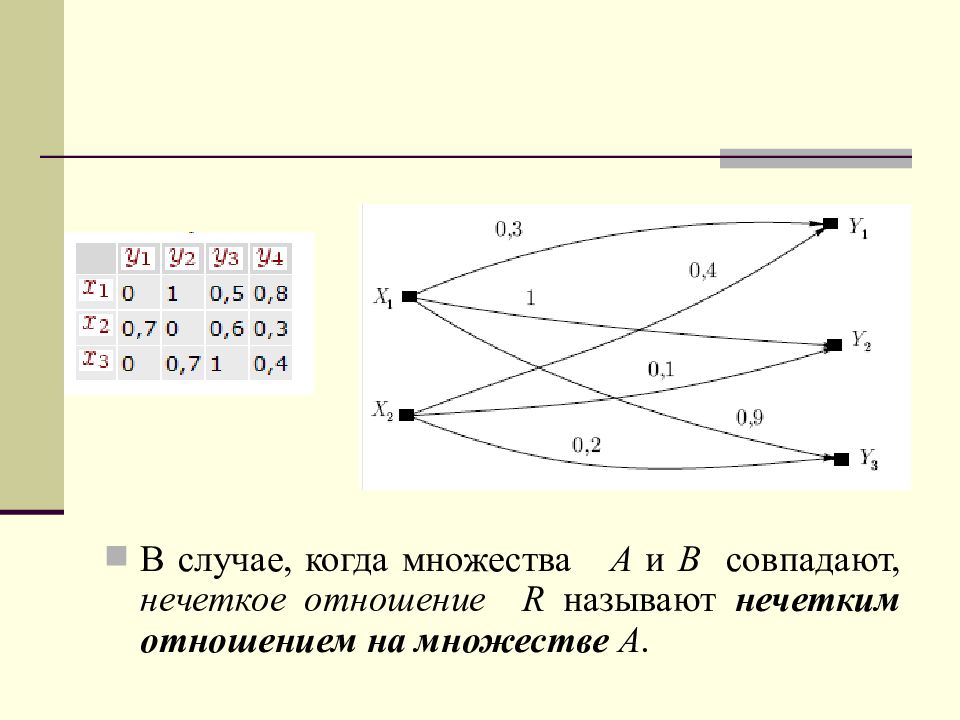
Далее мы ограничимся рассмотрением лишь бинарных нечетких отношений, являющихся отображением на отрезок [0,1], т.е. Если множества A и B конечны, нечеткое отношение R между A и B можно представить с помощью его матрицы отношения, первой строке и первому столбцу которой ставятся в соответствие элементы множеств A и B, а на пересечении a - той строки и b - го столбца помещается элемент
Слайд 34
В случае, когда множества A и B совпадают, нечеткое отношение R называют нечетким отношением на множестве A.