Слайд 2: Понятие объема
За единицу измерения объемов принимают куб, ребро которого равно единице измерения отрезков. Единицы измерения объемов: мм 3 ;см 3 ;дм 3 ;м 3 ;км 3. 1 литр = 1 дм 3
Слайд 3: Основные свойства объемов
1 о. Равные тела имеют равные объемы. 2 о.Если тело составлено из нескольких тел, то объем равен сумме объемов этих тел.
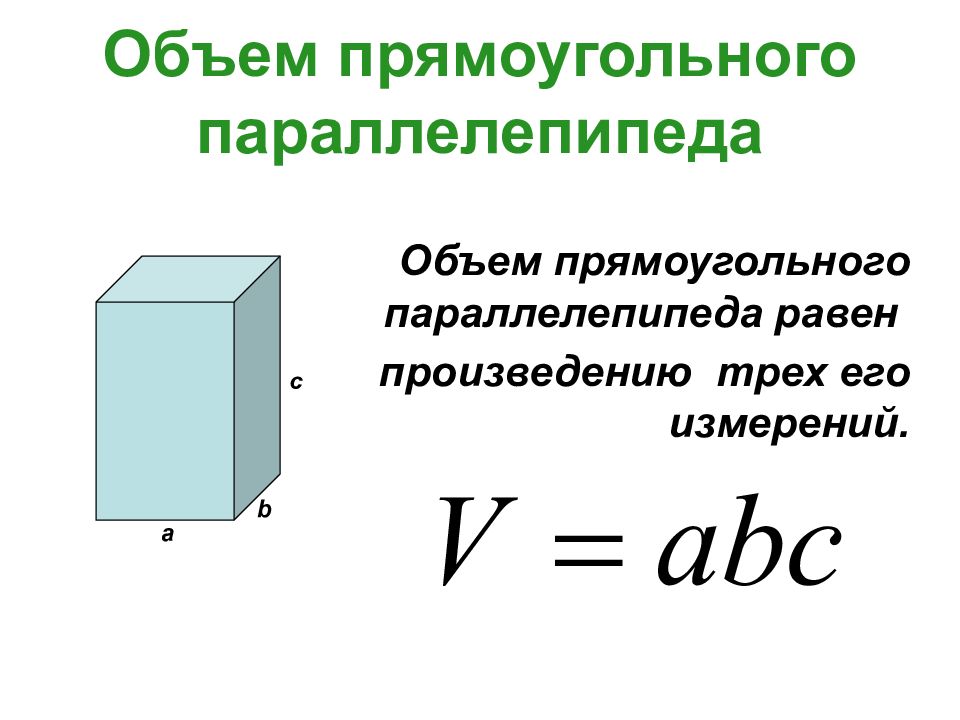
Слайд 4: Объем прямоугольного параллелепипеда
Объем прямоугольного параллелепипеда равен произведению трех его измерений. c a b
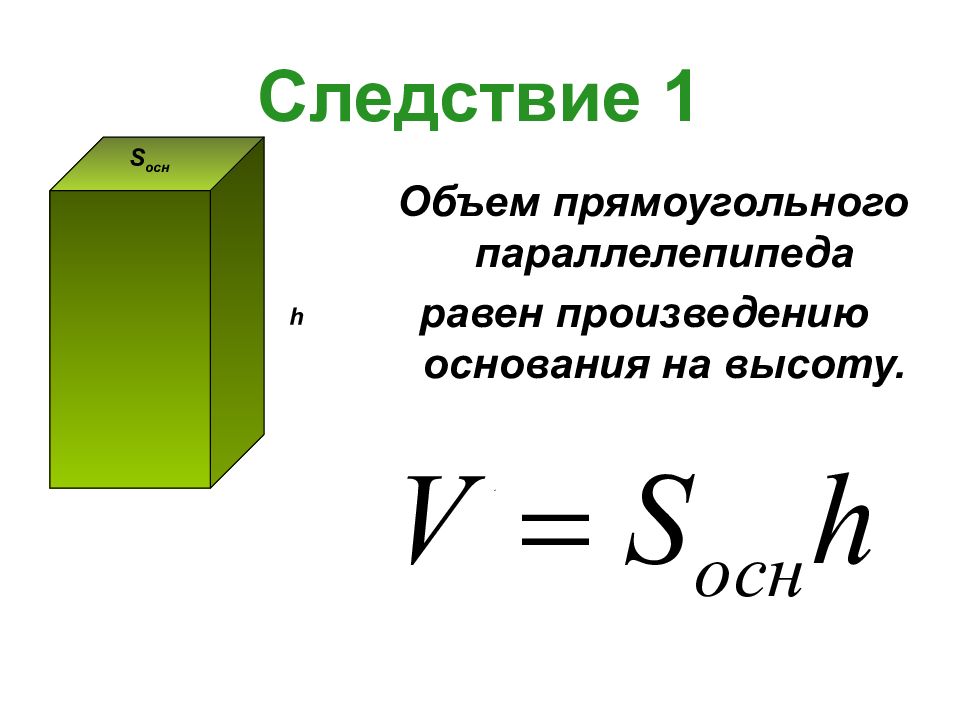
Слайд 5: Следствие 1
Объем прямоугольного параллелепипеда равен произведению основания на высоту. h S осн
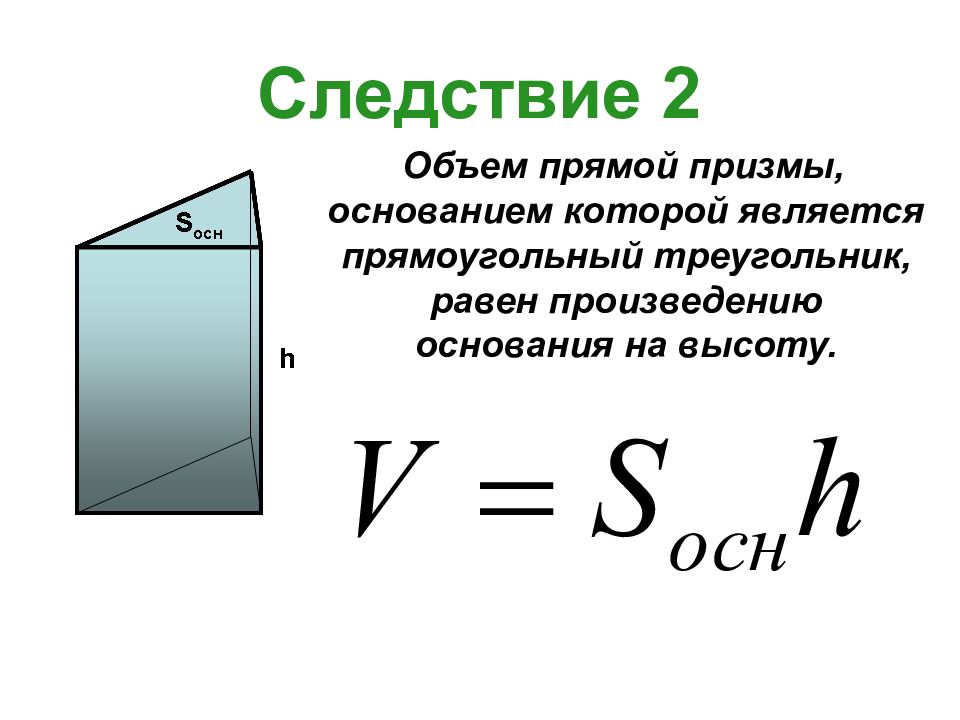
Слайд 6: Следствие 2
Объем прямой призмы, основанием которой является прямоугольный треугольник, равен произведению основания на высоту.
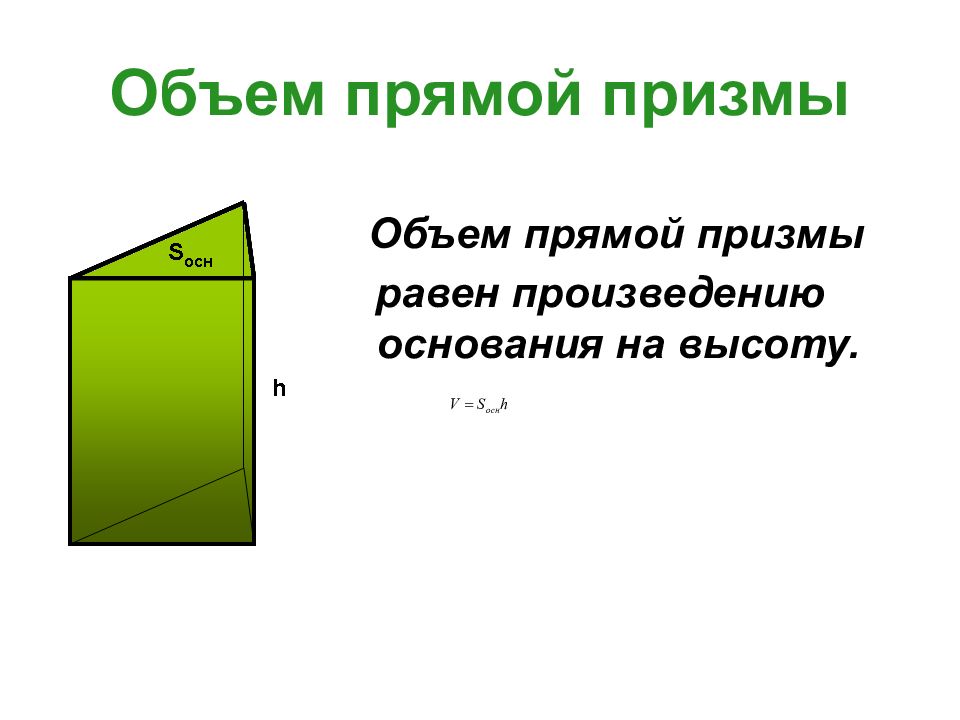
Слайд 7: Объем прямой призмы
Объем прямой призмы равен произведению основания на высоту.
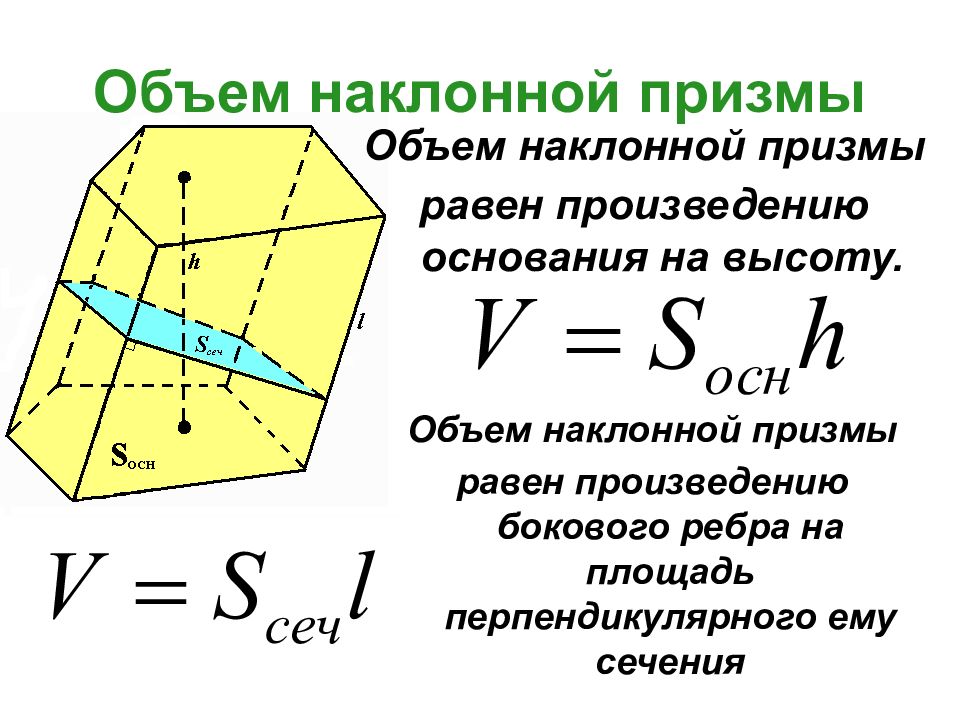
Слайд 9: Объем наклонной призмы
Объем наклонной призмы равен произведению основания на высоту. Объем наклонной призмы равен произведению бокового ребра на площадь перпендикулярного ему сечения
Слайд 10
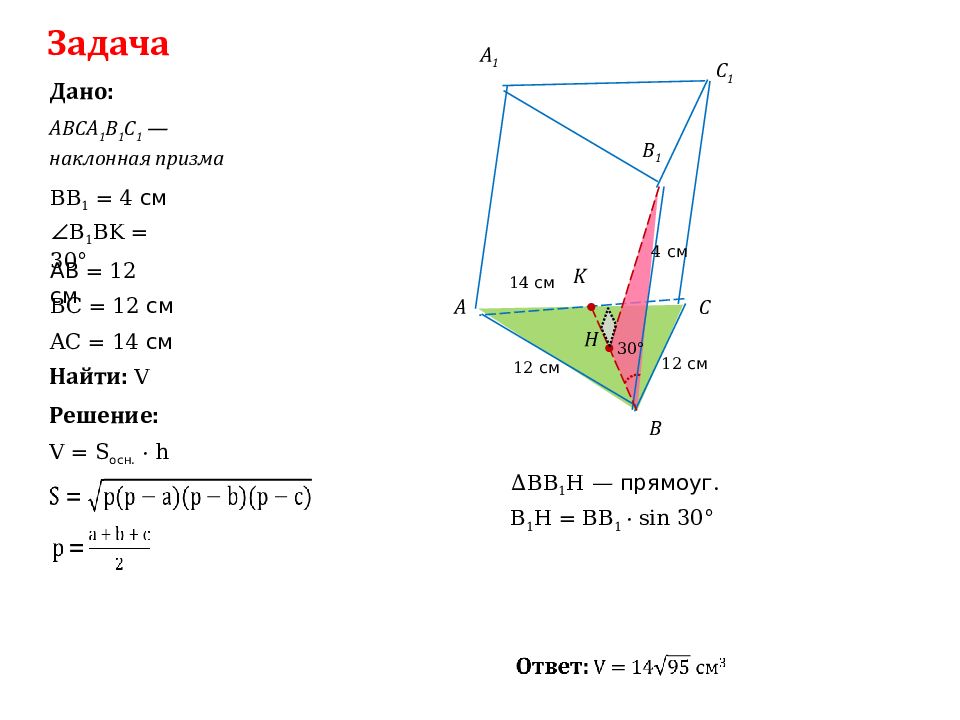
Задача Дано: Решение: Найти: V ABCA 1 B 1 C 1 — наклонная призма V = S осн. · h BC = 12 см АВ = 12 см AC = 14 см BB 1 = 4 см ∠B 1 BK = 30° ∆BB 1 H — прямоуг. B 1 H = BB 1 · sin 30° A C A 1 B 1 C 1 B K H 12 см 12 см 14 см 4 см 30°
Слайд 11
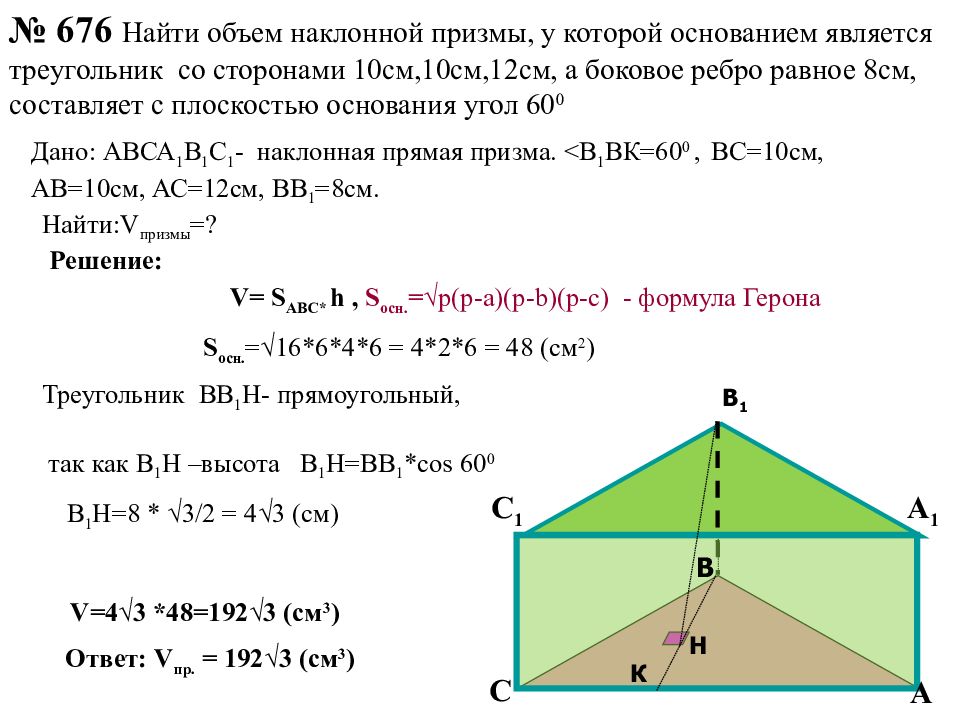
№ 676 Найти объем наклонной призмы, у которой основанием является треугольник со сторонами 10см,10см,12см, а боковое ребро равное 8см, составляет с плоскостью основания угол 60 0 V= S АВС* h, S осн. =√ р(р-а)(р- b )(р-с) - формула Герона S осн. =√16*6*4*6 = 4*2*6 = 48 (см 2 ) Ответ : V пр. = 192√3 (см 3 ) Треугольник ВВ 1 Н- прямоугольный, так как В 1 Н –высота В 1 Н=ВВ 1 * cos 60 0 Найти :V призмы = ? Решение : Дано : АВСА 1 В 1 С 1 - наклонная прямая призма. < В 1 ВК=60 0, ВС=10см, АВ=10см, АС=12см, ВВ 1 =8см. В 1 Н=8 * √3 / 2 = 4√3 (см) V= 4√3 *48=192√3 (см 3 ) С В 1 С 1 А 1 В К Н А
Слайд 12
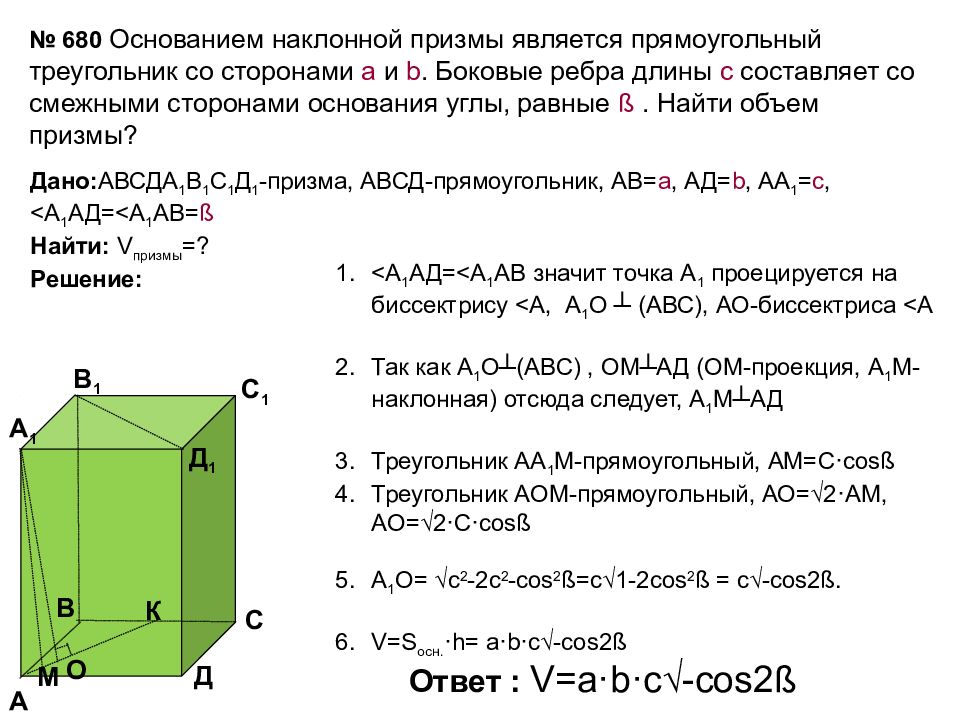
Дано : АВСДА 1 В 1 С 1 Д 1 -призма, АВСД-прямоугольник, АВ= а, АД= b, АА 1 = с, < А 1 АД= < А 1 АВ= ß Найти : V призмы = ? Решение : < А 1 АД= < А 1 АВ значит точка А 1 проецируется на биссектрису < А, А 1 О ┴ (АВС), АО-биссектриса < А Так как А 1 О┴(АВС), ОМ┴АД (ОМ-проекция, А 1 М-наклонная) отсюда следует, А 1 М┴АД Треугольник АА 1 М-прямоугольный, АМ=С· cosß Треугольник АОМ-прямоугольный, АО=√2·АМ, АО=√2·С·с osß А 1 О= √с 2 -2с 2 - cos 2 ß =с√1-2 cos 2 ß = с√- cos2ß. V=S осн. · h = а· b · c√-cos 2 ß Ответ : V= а· b · c√-cos 2 ß А В С Д В 1 А 1 Д 1 С 1 К М О № 680 Основанием наклонной призмы является прямоугольный треугольник со сторонами а и b. Боковые ребра длины с составляет со смежными сторонами основания углы, равные ß. Найти объем призмы ?
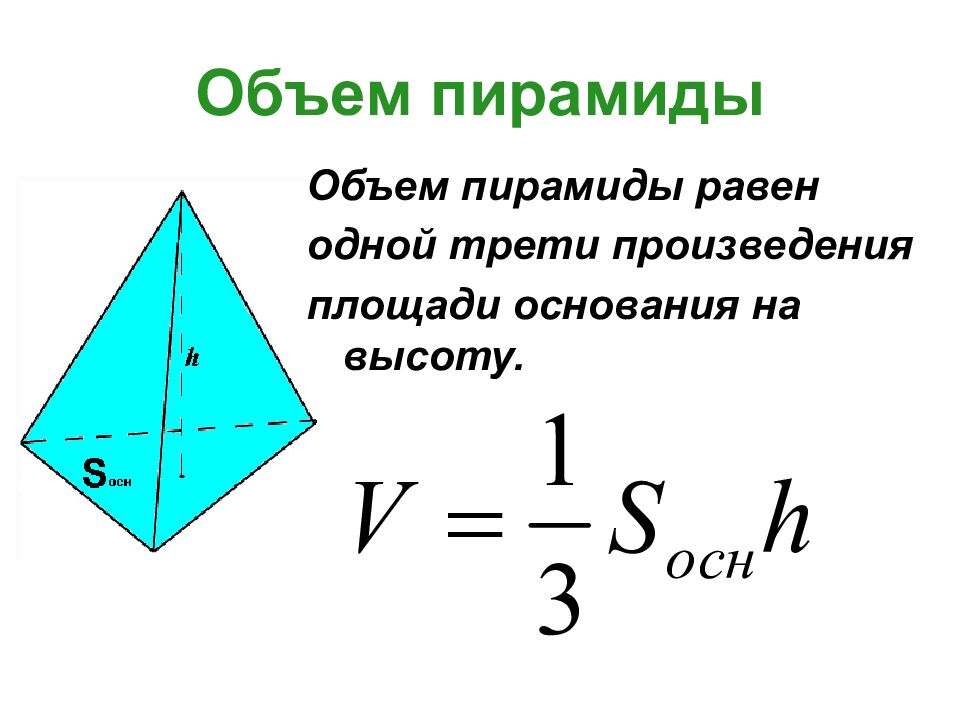
Слайд 13: Объем пирамиды
Объем пирамиды равен одной трети произведения площади основания на высоту.
Слайд 14
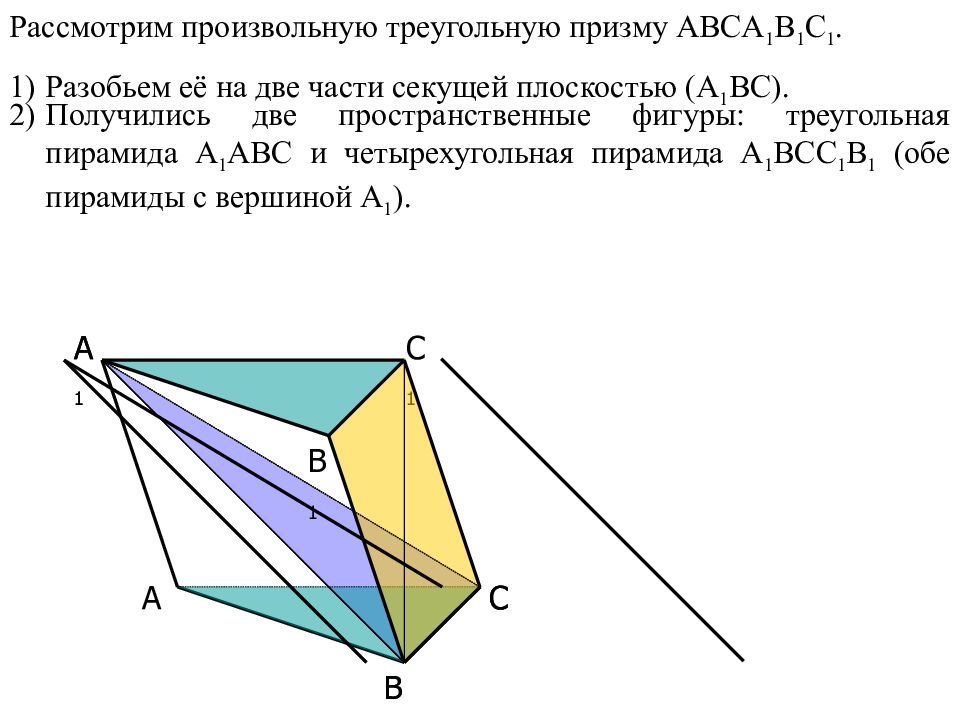
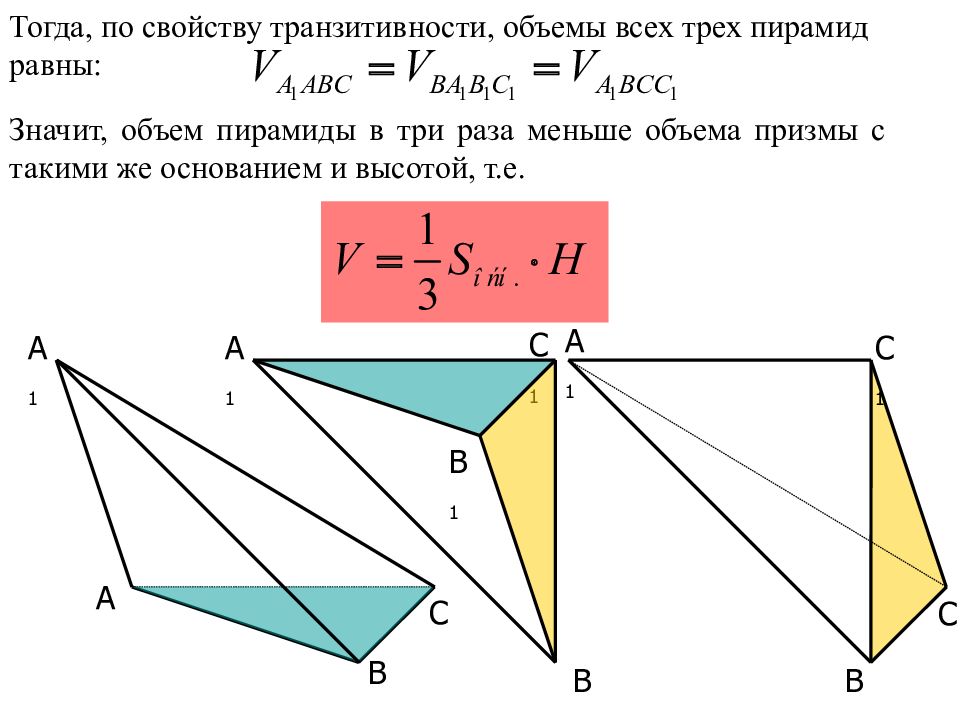
A B C B 1 A 1 C 1 C A 1 B Рассмотрим произвольную треугольную призму ABCA 1 B 1 C 1. Разобьем её на две части секущей плоскостью ( A 1 BC). Получились две пространственные фигуры: треугольная пирамида A 1 ABC и четырехугольная пирамида A 1 BCC 1 B 1 ( обе пирамиды с вершиной A 1 ).
Слайд 15
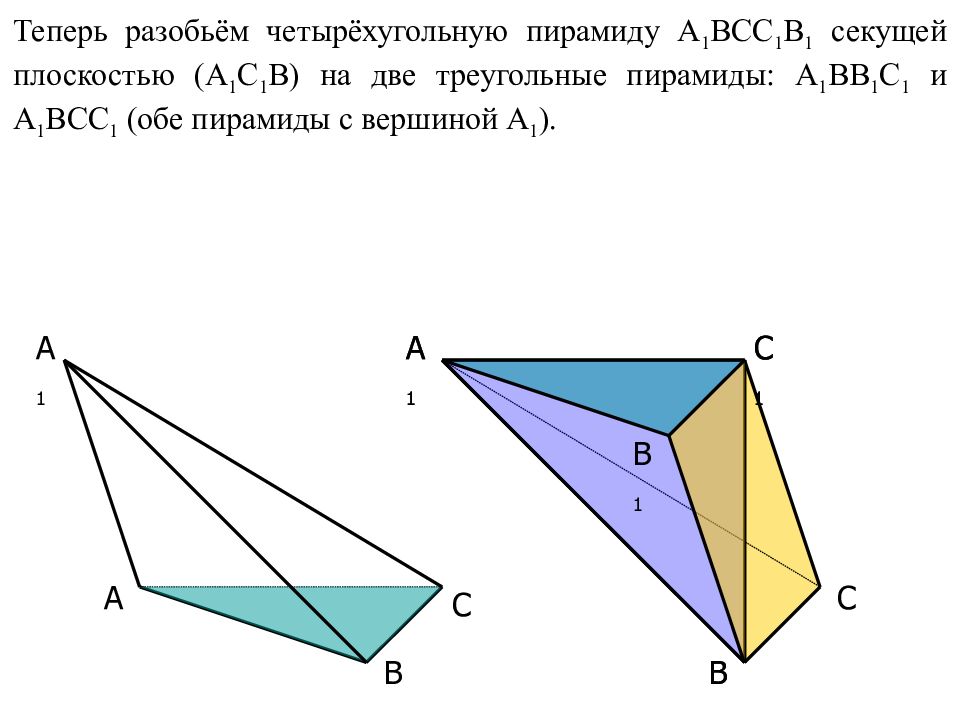
A C B 1 A 1 C 1 C A 1 B B Теперь разобьём четырёхугольную пирамиду A 1 BCC 1 B 1 секущей плоскостью ( A 1 C 1 B) на две треугольные пирамиды: A 1 BB 1 C 1 и A 1 BCC 1 (обе пирамиды с вершиной A 1 ). A 1 C 1 B
Слайд 16
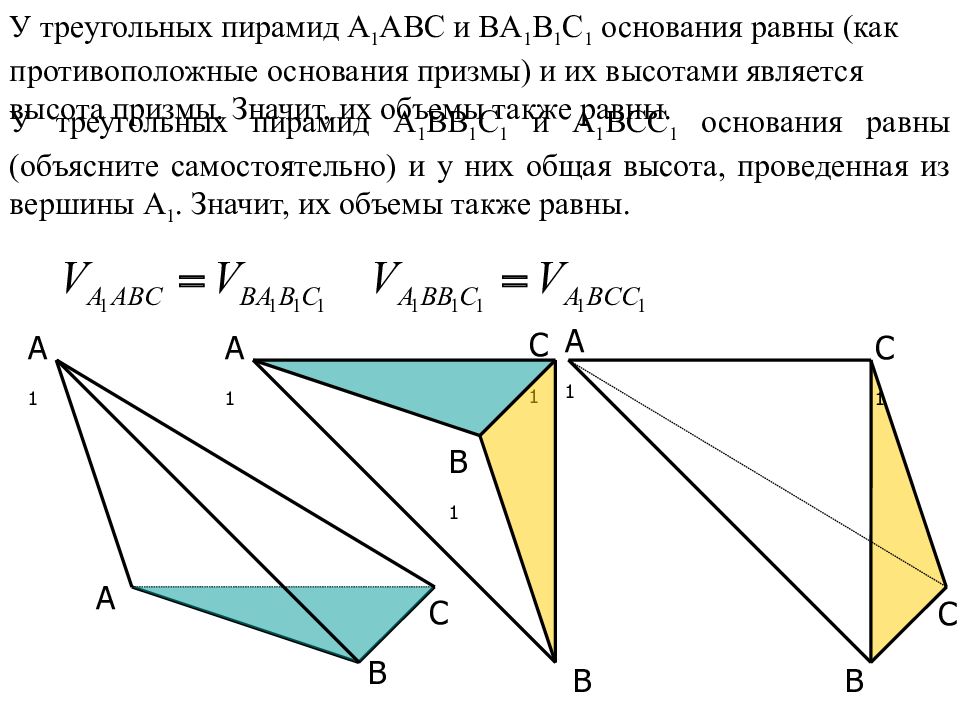
A C B 1 A 1 C 1 C A 1 B B A 1 C 1 B У треугольных пирамид A 1 ABC и BA 1 B 1 C 1 основания равны (как противоположные основания призмы) и их высотами является высота призмы. Значит, их объемы также равны. У треугольных пирамид A 1 BB 1 C 1 и A 1 BCC 1 основания равны (объясните самостоятельно) и у них общая высота, проведенная из вершины A 1. Значит, их объемы также равны.
Слайд 17
A C B 1 A 1 C 1 C A 1 B B A 1 C 1 B Тогда, по свойству транзитивности, объемы всех трех пирамид равны: Значит, объем пирамиды в три раза меньше объема призмы с такими же основанием и высотой, т.е.
Слайд 18
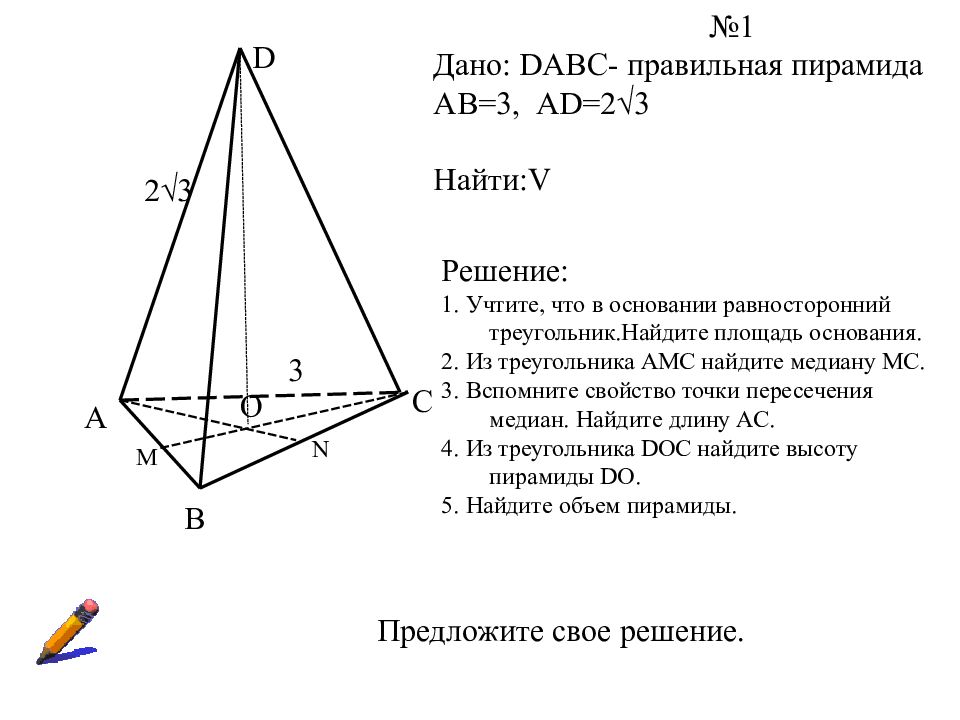
А В С D О М N №1 Дано: DABC- правильная пирамида АВ=3, AD=2 3 Найти: V Решение: 1. Учтите, что в основании равносторонний треугольник.Найдите площадь основания. 2. Из треугольника АМС найдите медиану МС. 3. Вспомните свойство точки пересечения медиан. Найдите длину АС. 4. Из треугольника DOC найдите высоту пирамиды DO. 5. Найдите объем пирамиды. Предложите свое решение. 3 2 3
Слайд 19
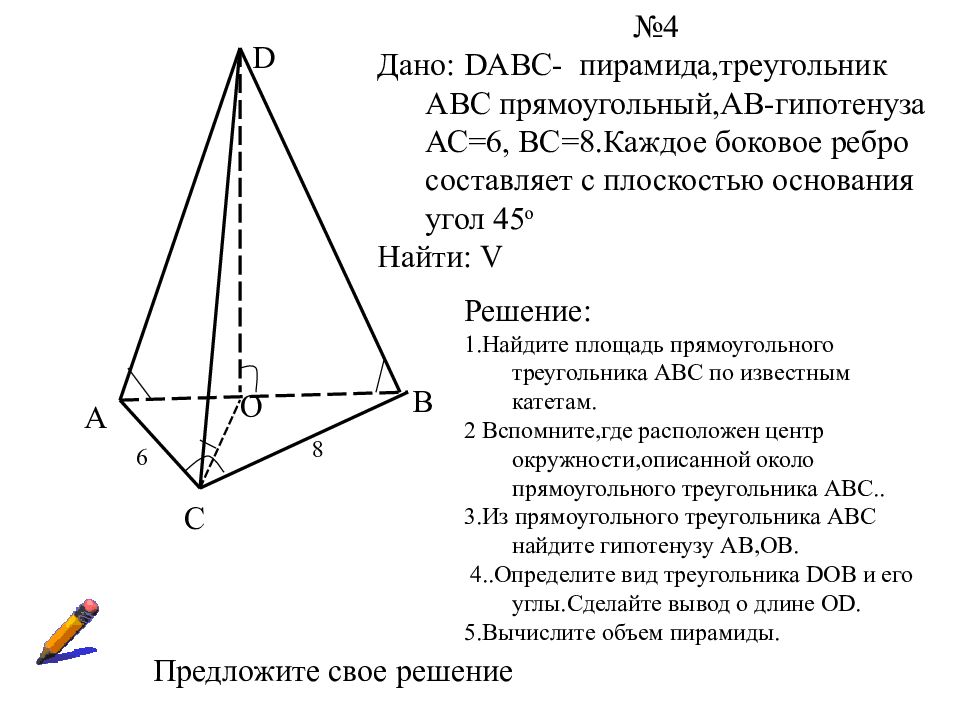
А С В D О 6 8 №4 Дано: DABC- пирамида,треугольник АВС прямоугольный,АВ-гипотенуза АС=6, ВС=8.Каждое боковое ребро составляет с плоскостью основания угол 45 о Найти: V Решение: 1.Найдите площадь прямоугольного треугольника АВС по известным катетам. 2 Вспомните,где расположен центр окружности,описанной около прямоугольного треугольника АВС.. 3.Из прямоугольного треугольника АВС найдите гипотенузу АВ,ОВ. 4..Определите вид треугольника DOB и его углы.Сделайте вывод о длине О D. 5.Вычислите объем пирамиды. Предложите свое решение
Слайд 20
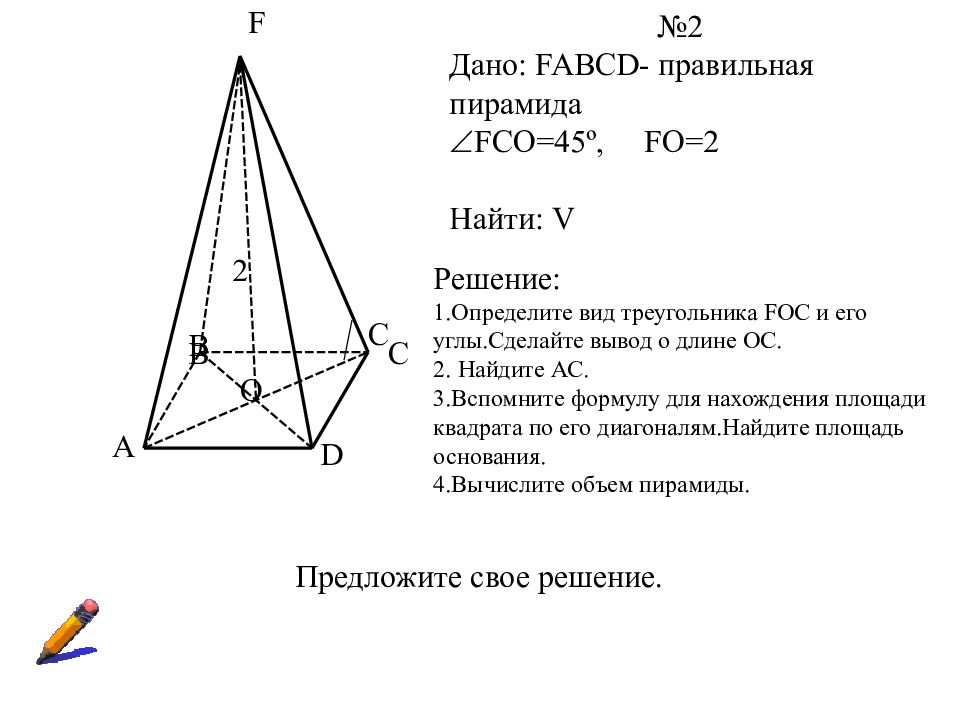
A B C D F O №2 Дано: FABCD- правильная пирамида FCO=45 º, FO=2 Найти: V B C 2 Решение: 1.Определите вид треугольника FOC и его углы.Сделайте вывод о длине ОС. 2. Найдите АС. 3.Вспомните формулу для нахождения площади квадрата по его диагоналям.Найдите площадь основания. 4.Вычислите объем пирамиды. Предложите свое решение.
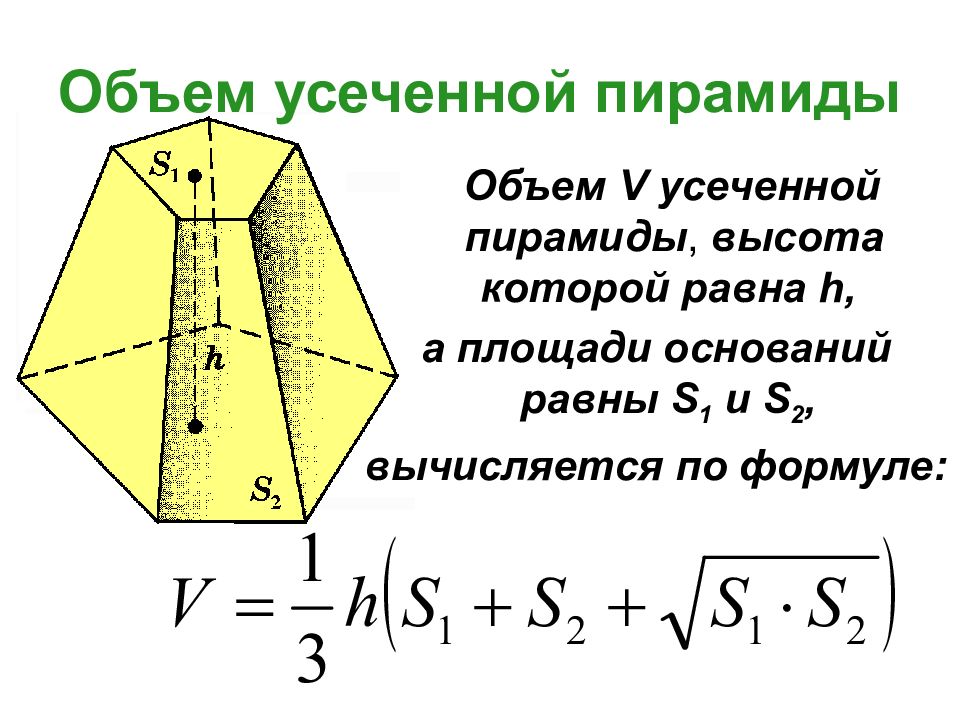
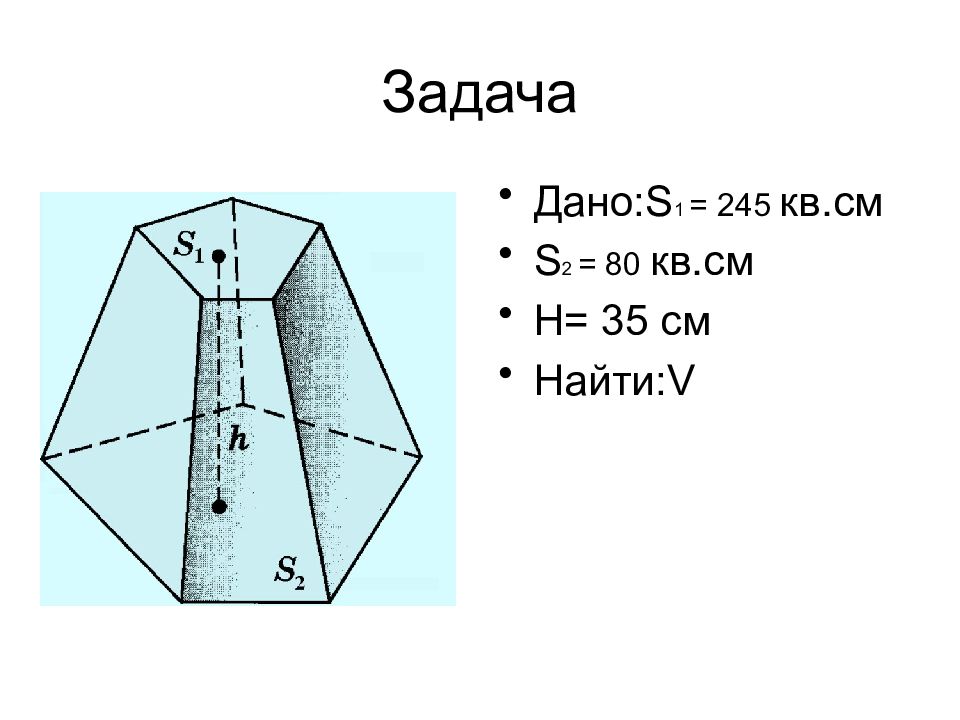
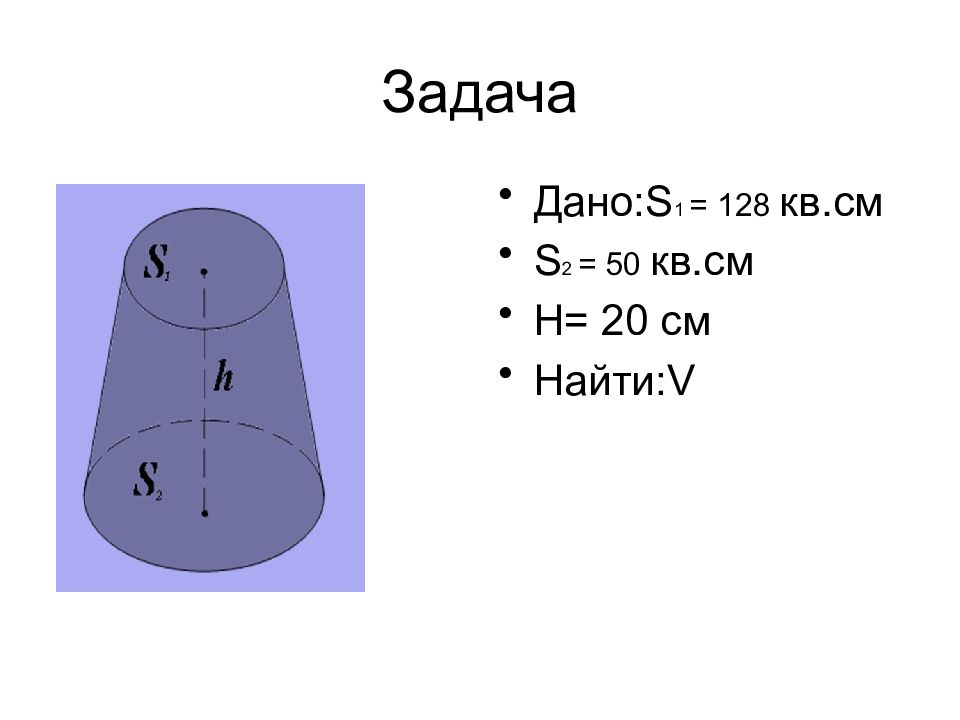
Слайд 21: Объем усеченной пирамиды
Объем V усеченной пирамиды, высота которой равна h, а площади оснований равны S 1 и S 2, вычисляется по формуле:
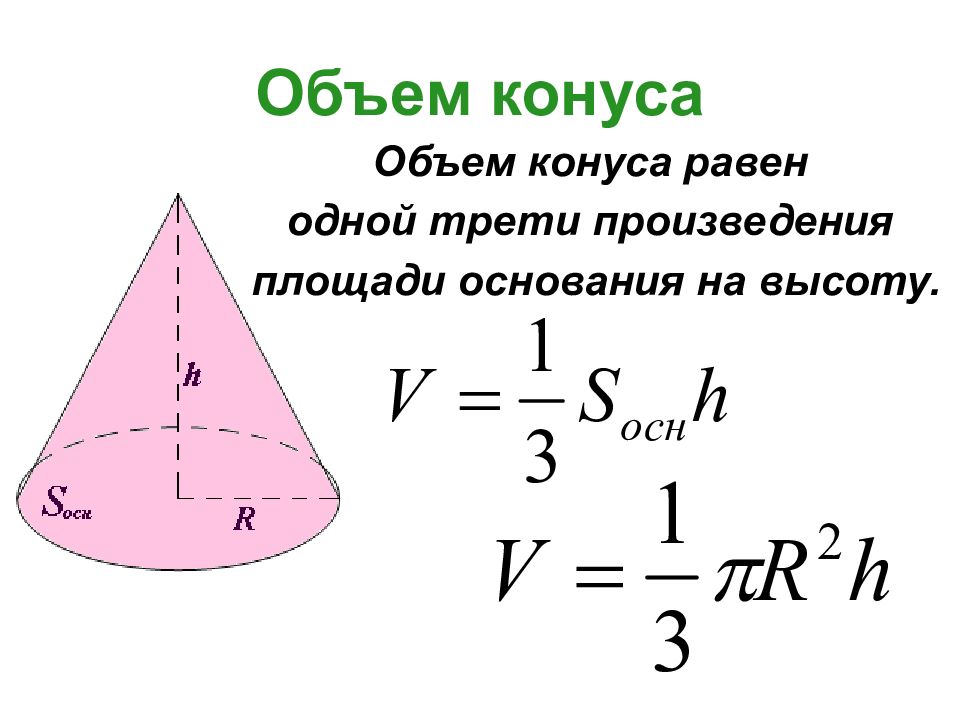
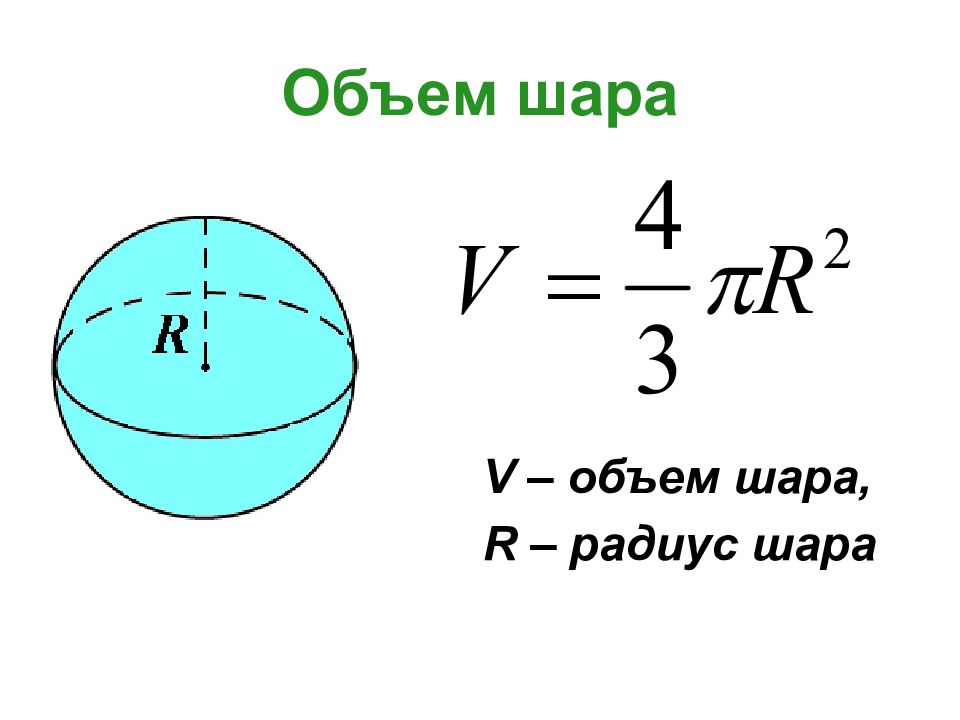
Слайд 23: Объем конуса
Объем конуса равен одной трети произведения площади основания на высоту.
Слайд 25
доказательство3 меню V тела вращ. = π ∫ H 0 2 f (x) dx. 3 1 = π 2 R H V конуса ∫ H 0 ∫ H 0 V конуса = π (kx) dx = 2 π 2 k 2 2 x dx = π * ( ) H R * H 3 x 3 0 = 2 H * 3 H 3 π R * 2 = = 2 H * 3 H 3 π R * 2 = 3 1 = π 2 R H R A C H O x y H y = kx α
Слайд 27
Задача 1. (объем конуса) Авиационная бомба среднего калибра дает при взрыве воронку диаметром 6 м и глубиной 2 м. Какое количество земли (по массе) выбрасывает эта бомба, если 1 м3 земли имеет массу 1650 кг? Решение: O A C 2м B 3 м * 3 * 2 = 6 (м ) 2 3 π P = 1650 * 6 * 3,14 31086 кг 31 т. ≈ ≈ Ответ: P = 31 т. 3 1 = π 2 R H V = 3 1 π
Слайд 28
Задача 2. (Объем конуса) Смолу для промышленных нужд собирают, подвешивая конические воронки к соснам. Сколько воронок диаметром 10 см с образующей 13 см нужно собрать, чтобы заполнить 10-литровое ведро? Дано: Решение. коническая воронка D = 10 см L = 13 см V – ? меню O A C 13 B 5 3 1 = π 2 R H V = 3 1 π * 25 * 12 = 100 (см ) π 3 = = 100 см = 0,1 дм. 3 3 π π 2 2 13 - 5 = 12 ( ) H = √ n = = = 31,8 10 100 100 0,1 3,14 π ≈ Ответ: n 32 воронки. ≈
Слайд 29
Задача 3. (Объем конуса) «... Читал я где-то, что царь однажды воинам своим велел снести земли по горсти в кучу. И гордый холм возвысился, и царь мог с высоты с весельем озирать и дол, покрытый белыми шатрами, и море, где бежали корабли.» А.С. Пушкин «Скупой рыцарь» меню Это одна из немногих легенд, в которой при кажущемся правдоподобии нет и зерна правды. Докажите геометрически, что если бы какой-нибудь древний деспот вздумал осуществить такую затею, он был бы обескуражен мизерностью результата. Перед ним высилась бы настолько жалкая куча земли, что никакая фантазия не смогла бы раздуть ее в легендарный «гордый холм».
Слайд 30
Войско в 100 000 воинов считалось очень внушительным. V = 0,2 * 100 000 = 20 000 дм3 = 20 м3. Угол откоса Ј 45°, иначе земля начнет осыпаться. Возьмем угол откоса наибольшим возможным, т. е. 45° Дано: конус V = 20 м 3 a = 45° Найти: H конуса меню 3 1 = π 2 R H V конуса 1 горсть ≈ литров = 0,2 дм. 5 1 3 45° H = = 2,7 м. √ √ 3 3 V 3 π 3 * 20 3,14 ≈ Решение: Так как H = R, то :
Слайд 31: Объем усеченного конуса
Объем V усеченного конуса, высота которого равна h, а площади оснований равны S 1 и S 2, вычисляется по формуле:
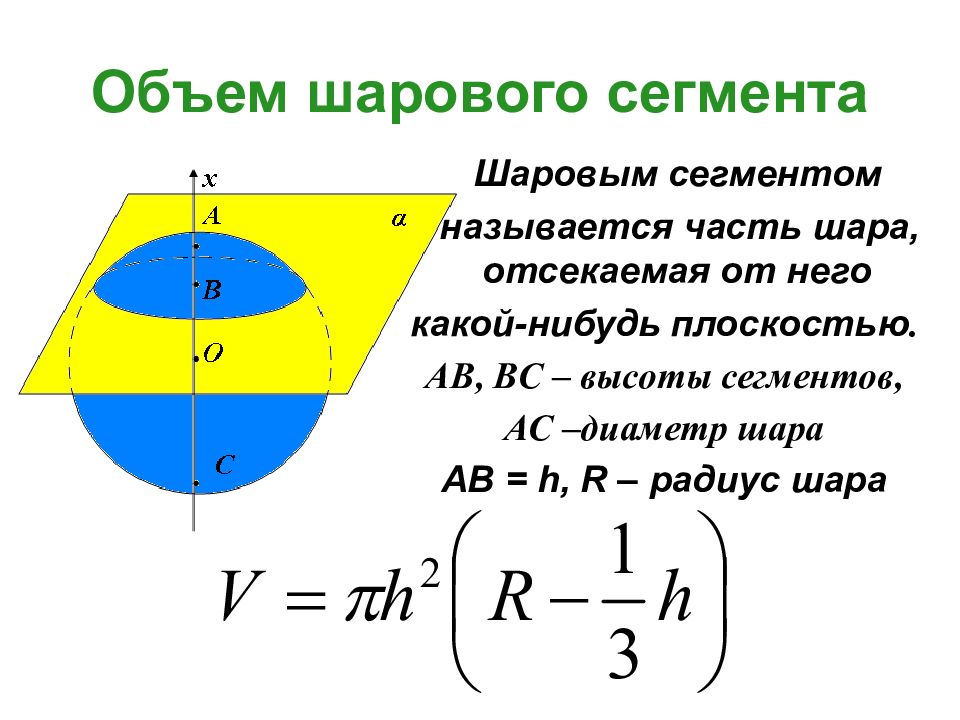
Слайд 34: Объем шарового сегмента
Шаровым сегментом называется часть шара, отсекаемая от него какой-нибудь плоскостью. AB, BC – высоты сегментов, АС –диаметр шара AB = h, R – радиус шара
Слайд 35: Объем шарового слоя
Шаровым слоем называется часть шара, заключенная между двумя параллельными плоскостями. ω (В, R 1 ) и ω (С, R 2 ) – основания шарового слоя, АВ – высота шарового слоя
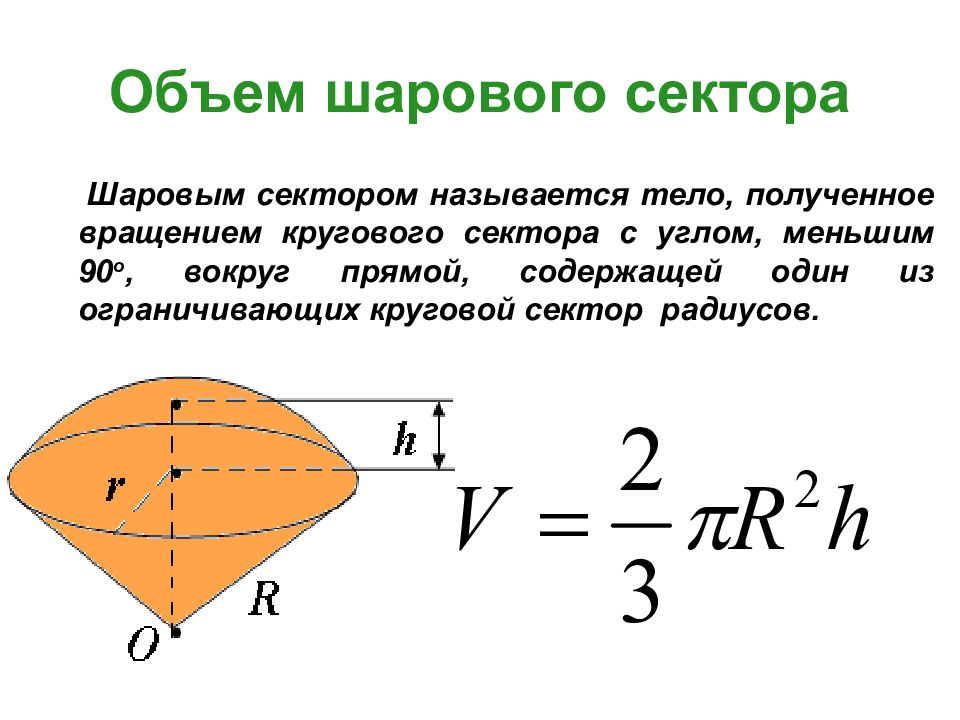
Слайд 36: Объем шарового сектора
Шаровым сектором называется тело, полученное вращением кругового сектора с углом, меньшим 90 о, вокруг прямой, содержащей один из ограничивающих круговой сектор радиусов.
Слайд 38: Математический диктант 2
1. Вычислите объём шара если его радиус R= 5см 2. Вычислите диаметр шара, если его объём V= 500 π /3 3. Вычислите площадь большего круга и длину окружности шара, если его объём V= 500 π /3 4. В цилиндр вписан шар радиуса R= 2. Найдите отношение V шара: V цилиндра
Слайд 39: Домашнее задание
Выучить п.74-82 В презентации выполнить задание математического диктанта 2. Ответы теста прислать каждому в свою папку на мой диск.
Последний слайд презентации: Объемы тел Геометрия, 11 класс: Литература
Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия. 7 – 9 классы: учебник для общеобразовательных учреждений. – М.: Просвещение, 2012. – 384 с. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия. 10 – 11 классы: учебник для общеобразовательных учреждений. – М.: Просвещение, 2012. – 256 с. Мордкович А.Г. Краткое справочное пособие по школьному курсу математики. Определения, теоремы, свойства, формулы, алгоритмы. – М.: Новая школа, 1994. – 48с. Звавич Л.И., Рязановский А.Р. Геометрия в таблицах. 7 – 11 классы: справочное пособие. – 11-е изд., стереотип. – М.: Дрофа, 2006. – 124с. Генденштейн Л.Э., Ершова А.С. Наглядный справочник по геометрии для 7 – 11 классов. – 3-е изд. – М.: Илекса, Харьков: Гимназия, 2000. – 96 с.