Расчет цепи синусоидального тока со смешанным соединением элементов. Содержание домашнего задания.
В домашнем задании предусматривается расчет электрической цепи со смешанным соединением элементов, состоящей из двух параллельных ветвей, в каждой из которых последовательно включено не менее двух элементов. В домашнем задании необходимо: 1. По исходной схеме (рис. 1) нарисовать электрическую схему согласно заданному варианту (табл. 1 ). Элементы, сопротивления которых равны нулю, исключаются из схемы. 2. Методом проводимостей рассчитать токи в параллельных ветвях и неразветвленной части цепи. 3. Вычислить активную, реактивную и полную мощности параллельных ветвей и всей цепи. 4. Построить векторную диаграмму токов и напряжений.
5. Изменяя одно из реактивных сопротивлений параллельной ветви, добиться, чтобы схема работала в режиме резонанса токов. Если в заданной цепи резонанс токов невозможен, ввести в одну из параллельных ветвей дополнительное реактивное сопротивление (индуктивность или емкость). 6. Построить векторную диаграмму токов и напряжений при работе цепи в резонансе токов. 7. При расчетах считать напряжение, приложенное к цепи, равным U=100 (В), сопротивления элементов заданы в табл. 1.
2.2 Пример расчета электрической цепи со смешанным соединением элементов Рассмотрим порядок расчета электрической цепи соответствующей варианту 72. Дано: R 1 =0 Ом, R 2 =20 Ом, X L1.1 =10 Ом, X C2.1 =0, X C1 =40 Ом, X L2 =20 Ом, X L1.2 =0 Ом, X C2.2 =0 Ом.. Данному варианту соответствует электрическая схема рис. 2.
Расчет производится в следующем порядке: Определяем полное сопротивление первой ветви: Ом. Определяем полное сопротивление второй ветви: Ом. Примечание : расчет вести до четырех значащих цифр. Определяем активную проводимость первой ветви: . Определяем реактивную проводимость первой ветви: См. Определяем полную проводимость первой ветви: См. Определяем активную составляющую первого тока: . Определяем реактивную составляющую первого тока: А. Определяем полный ток первой ветви: А. Определяем активную проводимость второй ветви: См. Определяем реактивную проводимость второй ветви: См. Определяем полную проводимость второй ветви: См. Определяем активную составляющую тока второй ветви: А. Определяем реактивную составляющую тока второй ветви: А. 14. П олный ток второй ветви: А. Определяем активную проводимость всей цепи: См.
Определяем реактивную проводимость всей цепи: См. Определяем полную проводимость всей цепи: См. 18. Определяем активную составляющую тока в неразветвленной части цепи: A. 19. Определяем реактивную составляющую тока в неразветвленной части цепи: A. 20. Определяем полный ток в неразветвленной части цепи: A. 21. Определяем коэффициент мощности первой ветви: . 22. Определяем коэффициент мощности второй ветви: .
23. Определяем коэффициент мощности всей цепи: 24. Определяем полную мощность первой ветви: В. 25. Определяем активную мощность первой ветви: . 26. Определяем реактивную мощность первой ветви: ВАр. 27. Определяем полную мощность второй ветви: В. 28. Определяем активную мощность второй ветви: Вт.
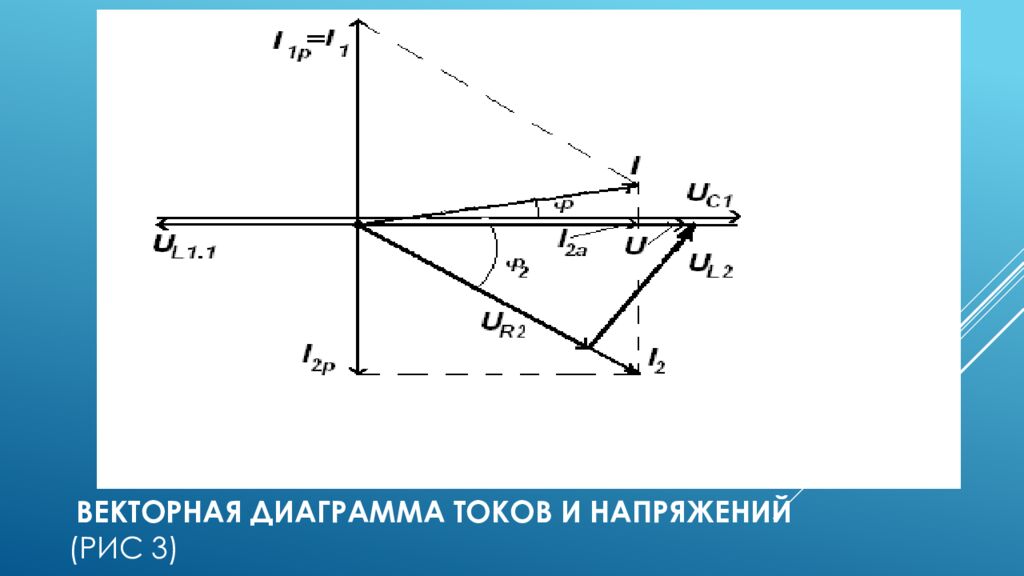
29. Определяем реактивную мощность второй ветви: ВАр. 30. Определяем полную мощность всей цепи: В. 31. Определяем активную мощность всей цепи: Вт. 32. Определяем реактивную мощность всей цепи: ВАр. 33. Векторная диаграмма токов (рис 3)строится на основании первого закона Кирхгофа для цепей синусоидального тока: .
Векторная диаграмма токов строится в следующем порядке: 33.1 За базовую ось принимаем вектор напряжения U, который является общим для обеих параллельных ветвей. Строим этот вектор горизонтально в масштабе m U. 33.2 По активной и реактивной составляющей первого тока строится вектор тока I 1. Но так как активная составляющая первого тока I 1a =0, то полный ток I 1 будет равен реактивной составляющей I 1р, которая имеет емкостный характер и опережает вектор напряжения U на угол 90° ( X=X L1.1 – X C1 <0 ). Этот вектор строим перпендикулярно к вектору напряжения U против часовой стрелки ( φ 1 =-90° ) в масштабе m 1. 33.3 Аналогично строим вектор тока второй ветви. Активная составляющая тока I 2a совпадает по фазе с вектором напряжения U, реактивная составляющая тока второй ветви I 2р носит индуктивный характер ( X 2 =X L2 >0 ) и отстает от вектора напряжения U на угол 90°. Этот вектор строим перпендикулярно к вектору напряжения по часовой стрелке. Вектор полного тока второй ветви будет равен диагонали параллелограмма построенного на векторах I 2a и I 2р. 34. Векторная диаграмма напряжений для первой ветви строится на основании второго закона Кирхгофа: .
Векторная диаграмма напряжений строится в следующем порядке: 34.1 Строится вектор падения напряжения на индуктивном сопротивлении X L1.1, модуль которого равен: B. На индуктивности напряжение опережает ток на угол 90°, поэтому этот вектор строим перпендикулярно вектору тока I 1 против часовой стрелки. 34.2 Из конца вектора U L1.1 строится вектор падения напряжения на емкостном сопротивлении X C1 , модуль которого равен: B. На емкости напряжение отстает от тока на угол 90°, поэтому этот вектор строим перпендикулярно вектору тока I 1 по часовой стрелке. Если вычисления и построения сделаны верно, то конец вектора U C1 будет совпадать с концом вектора U.
35. Векторная диаграмма напряжений для второй ветви строится на основании второго закона Кирхгофа: Векторная диаграмма напряжений для второй ветви строится в следующем порядке: 35.1 Строится вектор падения напряжения на активном сопротивлении R 2, модуль которого равен На активном сопротивлении напряжение и ток совпадают по фазе, поэтому этот вектор падения напряжения строим совпадающим по направлению с вектором тока I 2. 35.2 Из конца вектора U R2 строится вектор падения напряжения на индуктивном сопротивлении X L2, модуль которого равен: Напряжение на индуктивности опережает ток на угол 90°, поэтому этот вектор строим перпендикулярно вектору тока I 2 против часовой стрелки. Если вычисления и построения сделаны верно, конец вектора напряжения U L2 будет совпадать с концом вектора U.
36. Для обеспечения резонанса токов в электрической схеме с двумя параллельными ветвями должны выполняться следующие условия: параллельные ветви должны иметь разный характер проводимостей (одна индуктивный, другая емкостный). реактивные проводимости параллельных ветвей должны быть равны по модулю, т.е.: В данном варианте первое условие выполняется, т.к. первая ветвь носит емкостный, а вторая – активно-индуктивный характер. Для достижения резонанса токов, т.к. необходимо в первую ветвь включить дополнительно емкость, величину сопротивления которого можно вычислить следующим образом:
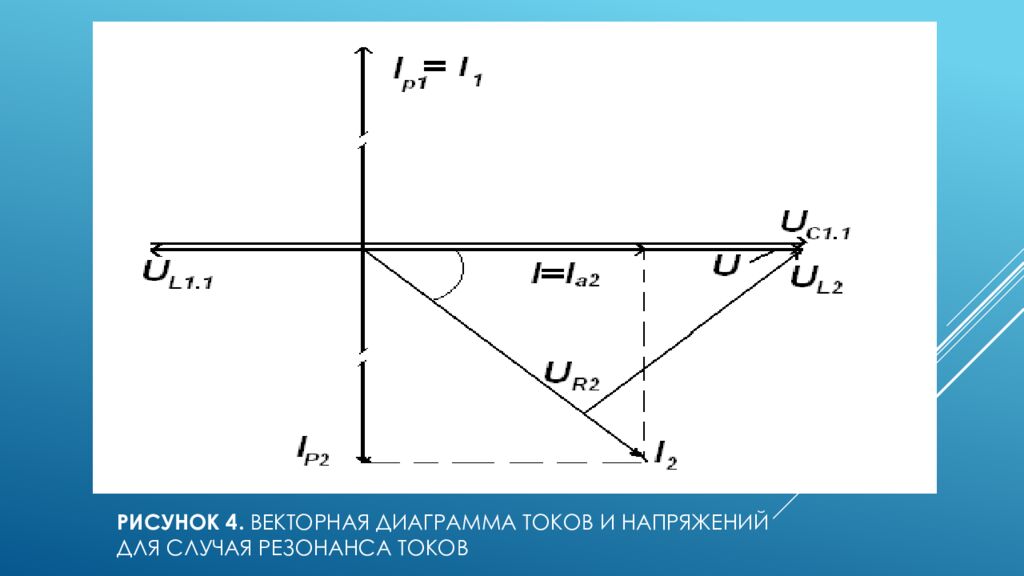
37. После включения дополнительной емкости в первую ветвь изменится ток в этой ветви и падения напряжения на индуктивности и емкости. См, А, А, В, В. Векторная диаграмма, построенная аналогично п.п. 33-35, представлена на рис. 4.
№ Величина сопротивления (Ом) R 1 X L1.1 X C1 X L1.2 R 2 X C2.1 X L2 X C2.2 1 0 0 40 20 20 30 0 10 2 0 10 0 20 20 0 20 10 3 0 10 40 20 20 0 10 20 4 0 10 40 20 20 0 0 10 5 10 0 0 20 0 30 20 10 6 10 0 40 0 0 30 20 0 7 10 0 40 20 0 30 0 10 8 10 10 0 20 0 0 20 10 9 0 0 40 20 20 30 20 0 10 0 10 0 20 20 30 0 0 11 0 10 40 0 20 0 20 10 12 0 10 40 20 20 0 20 0 13 10 0 40 0 0 30 20 10 14 10 0 40 20 0 30 20 0 15 10 10 0 0 0 30 0 10 16 10 10 40 0 0 0 20 10 17 0 10 0 20 20 30 0 10 18 0 10 40 0 20 30 0 0 19 0 10 40 20 20 0 20 10 20 10 0 0 20 20 0 0 10 21 10 0 40 20 0 30 20 10 22 10 10 0 0 0 30 20 0 23 10 10 0 20 0 30 0 10 24 0 10 0 20 20 30 20 0 25 0 10 40 0 20 30 0 10 26 0 10 40 20 20 30 0 0 27 10 0 0 20 20 0 20 0 28 10 0 40 0 20 0 0 10 Таблица15.1
