Первый слайд презентации: Определения математики
«…чистая математика имеет своим объектом пространственные формы и количественные отношения действительного мира, стало быть весьма реальный материал. Тот факт, что этот материал принимает чрезвычайно абстрактную форму, может лишь слабо затушевать его происхождение из внешнего мира». Ф. Энгельс «В своей аксиоматической форме математика представляется скоплением абстрактных форм – математических структур, и оказывается, что некоторые аспекты экспериментальной действительности как будто в результате предопределения укладываются в некоторые из этих форм». Н. Бурбаки
Слайд 2: Периоды развития математики
1. Период зарождения математики до VI-V вв. до н. э. 2. Период развития математики о т VI-V вв. до н. э. по XVI в. н. э. 3. Период создания математики переменных величин от XVII в. по сер. I Х в. 4. Современный период развития математики от. сер. I Х в. по наши дни
Слайд 3: Свойства системы аксиом:
полнота независимость непротиворечивость Геометрические системы Эвклида Лобачевского Римана
Возникают неевклидовые геометрические системы. Новые математические теории возникают из внутренних. потребностей самой математики Значительно расширяется область приложения математики.
Слайд 5: Теория множеств
Множество – первичное понятие математики. «Множество - объединение в одно целое объектов, хорошо различимых нашей интуицией или нашей мыслью…. Множество есть многое, мыслимое нами как единое.» Георг Кантор (1845-1918 )
Слайд 6: Основные понятия теории множеств
А={ a 1 ; a 2 ;…; a n …}, где a 1 ; a 2 ;…; a n …- элементы множества Способы задания : перечисление элементов и описание свойств. Пустое множество не имеет ни одного элемента. Равные множества состоят из одних и тех же элементов или оба пустые. Множество А называется подмножеством В, если все элементы множества А принадлежат множеству В. Булеан множества – множество всех его подмножеств. Мощность множества – количество его элементов.
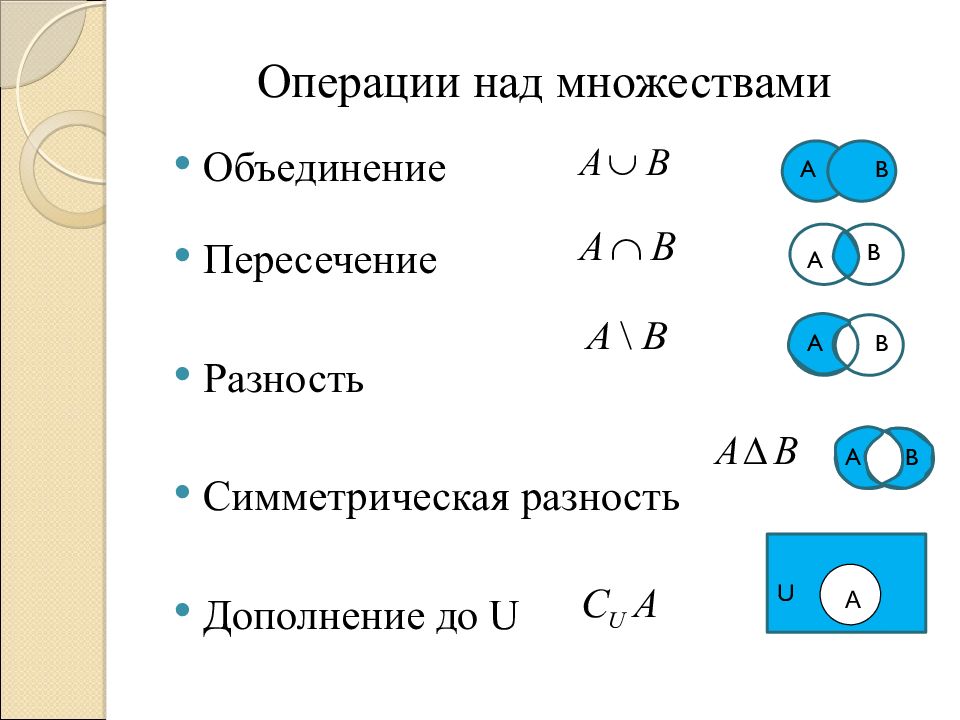
Слайд 7: Операции над множествами
Объединение Пересечение Разность Симметрическая разность Дополнение до U U A B A B A A B B А
Слайд 8: Декартовое произведение двух множеств А и В (обозначается )
- множество всех пар вида ( а;в ), где а А; в В Пример: = - декартовый квадрат множества А Пример: А={1;2;3;4}; B ={4;6}
Слайд 9: Отношения на множествах Отношение – любая зависимость между элементами одного или нескольких множеств
Виды отношений на множествах Унарные (1-местные) Бинарные (2-местные) Тернарные (3 –местные )
Слайд 10: Свойства бинарных отношений на множестве А
Рефлексивность Антирефлексивность Симметричность Антисимметричность Транзитивность
Слайд 11: Типы бинарных отношений:
эквивалентность ( рефлексивность, симметричность, транзитивность) отношение порядка … строгого ( антирефлексивность, антисимметричность, транзитивность) нестрогого ( рефлексивность, антисимметричность, транзитивность) толерантность ( рефлексивность, симметричность )
Слайд 12: Способы задания бинарных отношений
перечислением пар с помощью матрицы графом
Слайд 14: Правила комбинаторики
Пусть элемент А можно выбрать способами, элемент В - способами. Тогда: А или В можно выбрать способами; А и В можно выбрать способами. Правила верны и для большего числа элементов.
Слайд 15: Основные понятия комбинаторики
Размещение из - - упорядоченное подмножество из m элементов множества, которое содержит n элементов. Число размещений из
Слайд 16: Основные понятия комбинаторики
Перестановка из n элементов – это размещение из n элементов по n Число перестановок из n элементов
Слайд 17: Основные понятия комбинаторики
Сочетание из - неупорядоченное подмножество из m элементов, множества, которое содержит n элементов. Число сочетаний из