Первый слайд презентации: теория ВЕРОЯТНОСТЕЙ
1. Предмет теории вероятностей. Частота. Геометрическая вероятность. Случайные события, операции над событиями и отношения между ними. Пространство элементарных событий. Классическое определение вероятности. Теорема сложения вероятностей.
Слайд 2: Случайные события
Теория вероятностей занимается изучением случайных событий и их вероятностей. Событие называется случайным, если в результате испытания оно может произойти или не произойти.
Слайд 3: Случайные события
Все события можно разделить на три типа : невозможное событие ( ) – это такое событие, которое в результате испытания не может произойти; достоверное событие ( ) – это событие, которое в результате испытания обязательно происходит; случайные события ( А, В, С...), т.е. такие, которые в результате испытания могут произойти, а могут и не произойти.
Слайд 4: Вероятность случайного события
Вероятность P(A) случайного события А – это число, отражающее меру возможности появления события А в данном испытании. Отметим, что 0 ≤ Р(А) ≤ 1; Р( )= 0; Р( ) = 1.
Слайд 5: Относительная частота
Относительной частотой события А в серии испытаний называется число г де k – число испытаний, при которых событие А произошло; n – число всех проведенных испытаний.
Слайд 6: Устойчивость относительных частот
Длительные наблюдения показывают, что имеет место свойство устойчивости относительных частот: при проведении нескольких серий из n испытаний относительные частоты каждой из этих серий будут примерно одинаковыми; с увеличением числа испытаний n относительные частоты все меньше и меньше будут отклоняться друг от друга.
Слайд 7: Статистическая вероятность события
Если эти относительные частоты разумным образом округлить, то полученное таким образом число P(А) называют статистической вероятностью события А.
Слайд 8: Пространство элементарных исходов (событий)
Пространством элементарных исходов ( событий ) некоторого испытания (опыта) называют множество всех возможных результатов проведения этого испытания. Испытание Случайные события Пространство элементарных исходов ( ) Монету подбрасывают два раза А – число орлов и решек будет равно В – выпадет хотя бы один орел С – обе монеты выпадут орлом { ( о,о ),( о,р ),( р,о ),( р,р ) } Кубик (игр. кость) бросают два раза А – выпадет хотя бы одна шестерка В – сумма выпавших очков будет меньше десяти С – выпадут две единицы
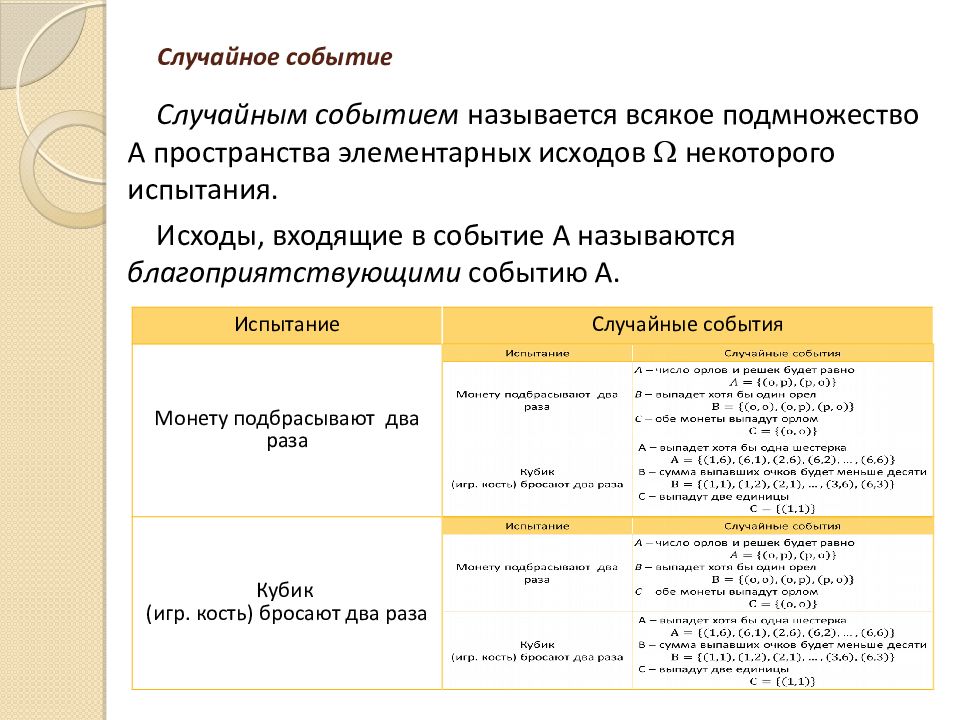
Слайд 9: Случайное событие
Случайным событием называется всякое подмножество А пространства элементарных исходов некоторого испытания. Исходы, входящие в событие А называются благоприятствующими событию А. Испытание Случайные события Монету подбрасывают два раза Кубик (игр. кость) бросают два раза
Слайд 10: Операции над случайными событиями
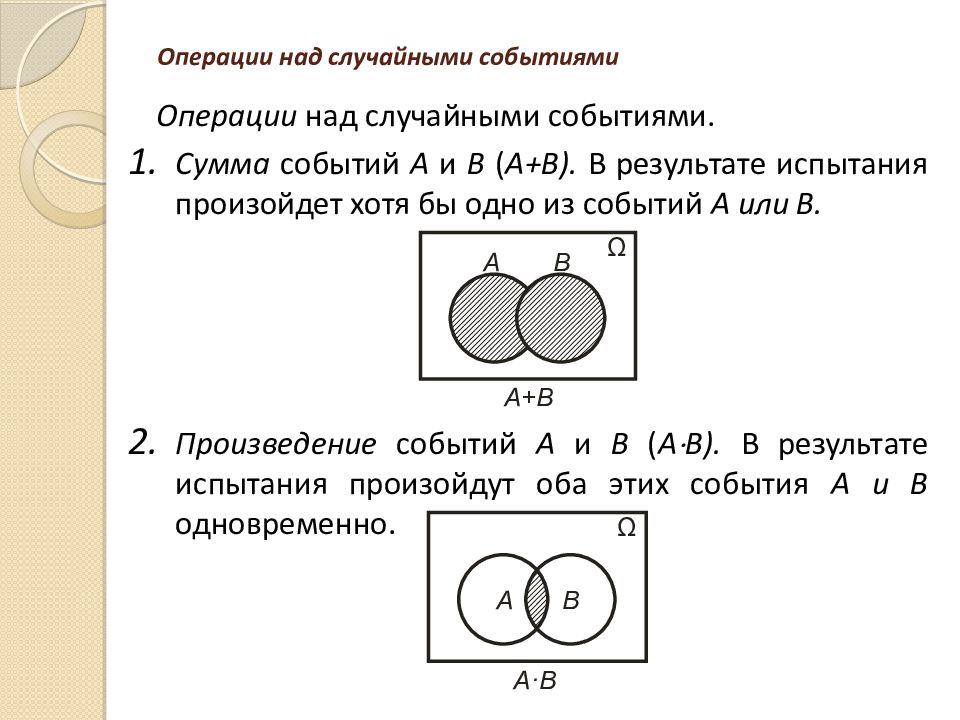
Операции над случайными событиями. Сумма событий А и В ( A+B). В результате испытания произойдет хотя бы одно из событий А или В. Произведение событий А и В ( А В). В результате испытания произойдут оба этих события А и В одновременно.
Слайд 11: Операции над случайными событиями
Случайные события А и В называются несовместными (несовместимыми), если в результате испытания они не могут произойти одновременно, т.е. А В = . Если же А В≠ , то события А и В называются совместными.
Слайд 12: Операции над случайными событиями
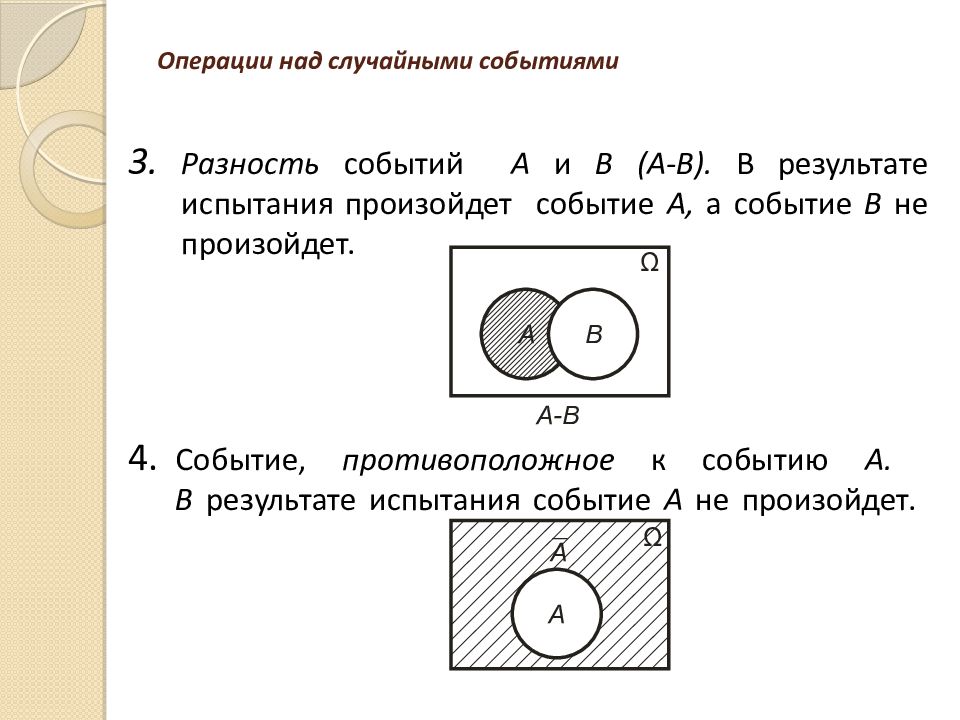
Разность событий А и В ( A-B ). В результате испытания произойдет событие А, а событие В не произойдет. Событие, противоположное к событию А. В результате испытания событие А не произойдет.
Слайд 13: теория ВЕРОЯТНОСТЕЙ
2. Условная вероятность. Независимость событий. Вероятность произведения событий. Теорема о полной вероятности. Формулы Байеса.
Слайд 14: Теоретическое определение вероятности
Вероятностью называется действительная функция Р(А), заданная на множестве случайных событий некоторого испытания (опыта), имеющая следующие свойства: Р(А) ≥ 0. Р(Ω) = 1. Если события А и В несовместны (АВ= ), то Р(А+В) = Р(А)+Р(В) (P А (В) - условная вероятность)
Слайд 15: Условная вероятность
Условная вероятности ( P А (В) ) события В при условии А – вероятность события В, вычисленн ая в предположении, что событие А произошло. События А и В называются независимыми, если вероятность одного из них не зависит от того, произошло или нет другое (Р (В)=Р А (В) или Р (А)=Р В (А) ).
Слайд 16: Свойства вероятности
Из определения получим следующие простейшие свойства вероятности: Р( ) =0 ; Р( А) = 1 - Р(А); формула умножения вероятностей: Р ( АВ)=Р(А)∙Р А (В) или Р(АВ) = Р(А)∙Р(В) (для независимых событий); формула сложения вероятностей Р(А+В)=Р(А)+Р(В) – Р(АВ).
Слайд 17: Пример
Задача 1. Найти вероятность того, что при одном бросании игральной кости (кубика) выпадет четная цифра большая 3.
Слайд 18: Пример (задача 1)
Решение: Рассмотрим следующие элементарные исходы: А 1 - на кубике выпала цифра “1”; А 2 - на кубике выпала цифра “2”; ... А 6 - на кубике выпала цифра “6”. Исходы А 1 …А 6 образуют полную группу несовместных и равновероятных исходов (кубик симметричен). Событию А, описанному в задаче, благоприятствует два исхода: А 4 и А 6. Таким образом, n = 6, m = 2
Слайд 19: Пример
Задача 2. Из набора костей домино наугад извлекают одну кость. Какова вероятность того, что эта кость – дупль.
Слайд 20: Пример (задача 2)
Решение: В полном наборе костей домино – 28 штук, из них – 7 дуплей. Полную группу равновероятных и несовместных исходов образуют 28 исходов, 7 из которых благоприятствуют рассматриваемому событию А. Таким образом,
Слайд 21: Пример
Задача 3. Из колоды в 36 карт наудачу достают одну карту. Найти вероятность того, что эта карта – туз
Слайд 22: Геометрическое определение вероятности
Рассмотрим испытание, состоящее а том, что внутри заданной плоскости области Ω наугад отмечается точка М, Тогда для любой меньшей области D 1, лежащей в Ω можно рассмотреть событие А, состоящее в том, что отмеченная точка М окажется лежащей в D 1. Вероятность этого события вычисляется по формуле
Слайд 23: Пример
Задача 5. В квадрате со стороной 3 см наугад отмечается точка М. Найти вероятность того, что т. М окажется не дальше 1 см от ближайшей вершины квадрата.
Слайд 24: Пример (задача 5)
Решение: В данном случае область - это квадрат. Рассматриваемому событию А соответствует заштрихованная область D 1 – четыре круговых сектора радиуса 1 см. S = 3 2 = 9, S 1 = 1 2 =
Слайд 25: Пример
Задача 6. Наугад выбирают два числа: 0 ≤ x ≤ 2 и 0 ≤ y ≤ 1. Строится прямоугольник со сторонами x и y. Найти вероятность того, что его площадь будет больше 1.
Слайд 26: Пример (задача 6)
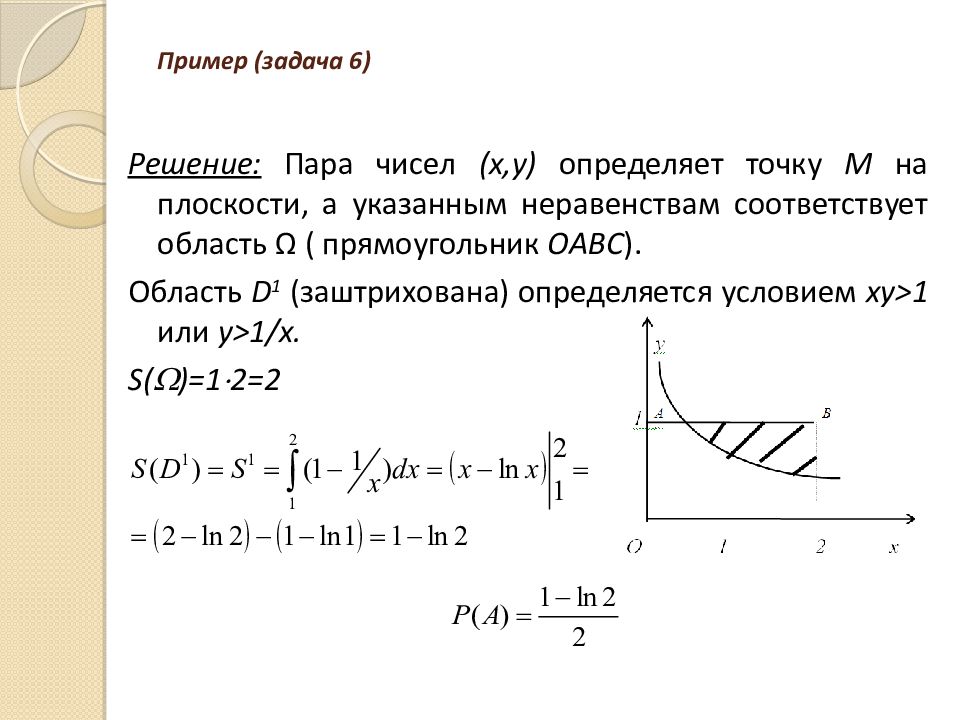
Решение: Пара чисел ( x,y ) определяет точку М на плоскости, а указанным неравенствам соответствует область Ω ( прямоугольник OABC ). Область D 1 (заштрихована) определяется условием xy >1 или y >1/ x. S( )=1 2=2
Слайд 27: Элементы комбинаторики
Во многих задачах непросто определить, что надо понимать под исходами, образуют ли они полную группу равновероятных и несовместных исходов, подсчитать их общее число n и число благоприятных исходов m. Для решения этих задач может помочь знание комбинаторных формул.
Слайд 28: Элементы комбинаторики
Правило произведения (умножения ). Рассмотрим несколько конечных множеств: A={a 1, a 2,…,a n }, B={b 1, b 2,…, b n }, …, C={c 1, c 2,…, c n } Тогда общее число всевозможных упорядоченных наборов ( a i1,b i2,…, c ik ) таких что можно найти по формуле:
Слайд 29: Элементы комбинаторики
Размещения c повторениями. Пусть A ={a 1, a 2,…,a n } – конечное множество из n элементов, k – натуральное число. Размещением из n элементов по k с повторением называется любой упорядоченный набор ( a i1,a i2,…, a ik ) в котором все элементы а i Є А. Согласно правилу произведения общее число размещений с повторениями из n по k равно
Слайд 30: Элементы комбинаторики
Размещения без повторений. Пусть A ={a 1, a 2,…,a n } – конечное множество из n элементов, k – натуральное число. Размещением из n элементов по k без повторений называется любой упорядоченный набор ( a i1,a i2,…, a ik ) в котором все элементы а i Є А являются различными. Общее число размещений без повторений из n по k равно
Слайд 31: Элементы комбинаторики
Перестановки. Перестановкой элементов конечного множества A ={a 1, a 2,…,a n } называется частный случай размещений без повторений, когда n=k. Следовательно, число всех перестановок n элементов равно :
Слайд 32: Элементы комбинаторики
Сочетания Сочетанием (без повторений ) из n элементов множества A ={a 1, a 2,…,a n } по k называется любой неупорядоченный набор из k элементов множества А (0≤ k≤n ). Следовательно каждое сочетание без повторений совпадает с подмножеством множества A. Для любого сочетания из k элементов число различных размещений из этих же элементов равно числу перестановок Р k. Поэтому Число всех сочетаний из n по k можно вычислить по формуле:
Слайд 33: Пример
Задача 7. Бросают два кубика. Какова вероятность того, что сумма выпавших на них цифр окажется больше шести?
Слайд 34: Пример (задача 7)
Решение: Элементарный исход данного испытания можно представить себе как пару чисел (i, j), где i - это цифра, выпавшая на первом кубике, j - на втором кубике. Следовательно, исходами являются размещения из 6 элементов по 2 с повторениями. Значит, можно найти число всех исходов : n=6 2 =36 Для подсчета числа благоприятных исходов удобно записать все исходы в виде таблицы:
Слайд 35: Пример (задача 7)
Решение: Событию А (сумма цифр больше 6) благоприятствуют те исходы, которые расположены в таблице ниже линии, проведенной над диагональю. Таким образом, m=1+2+3+4+5+6=21. Следовательно,
Слайд 36: Пример
Задача 8. Монету подбросили 5 раз. Найти вероятность того, что ровно один раз она упадет вверх “решкой ”.
Слайд 37: Пример (задача 8)
Решение: Любой исход данного испытания можно представить в виде пятибуквенного слова (с буквами О и Р). Например, исход ОРООР означает, что первый раз монета упала орлом, второй раз – решкой, третий раз – орлом, четвертый раз – орлом, пятый раз – решкой. Число всех таких слов вычисляется как число размещений из двух элементов по 5 с повторениями: n=2 5 =32. Указанному событию благоприятствует m=5 исходов: РОООО, ОРООО, ООРОО, ОООРО, ООООР.
Слайд 38: Пример
Задача 9. Из колоды в 36 карт по очереди наугад достают три карты (назад карты не возвращаются). Найти вероятность того, что вторая по счету из них будет тузом, а две другие – нет.
Последний слайд презентации: теория ВЕРОЯТНОСТЕЙ: Пример (задача 9)
Решение: Исходом данного испытания будет являться размещение из 36 элементов по 3 без повторений: n=36 35 34. Число благоприятных исходов можно подсчитать следующим образом: рассмотрим упорядоченную тройку карт, в которой первая карта – не туз, вторая – туз, третья – не туз. В этой тройке на первое место можно поставить любую из 32 карт (не тузов), на второе место - любого из 4 тузов, на третье место – любую из оставшихся 31 карты (не тузов). Общее число таких троек: m=32 4 31.