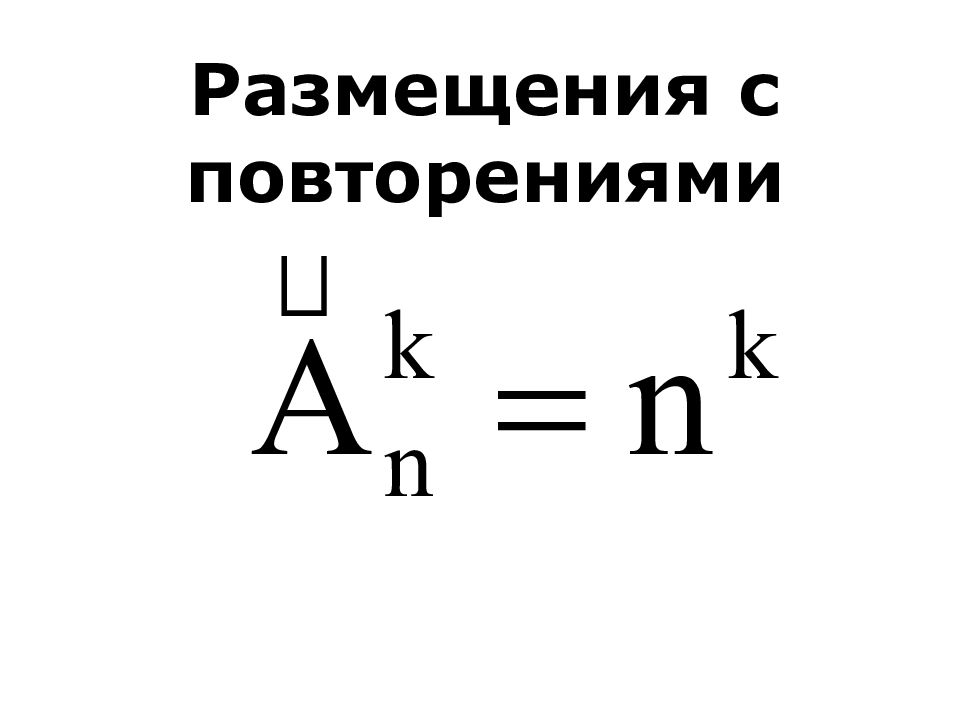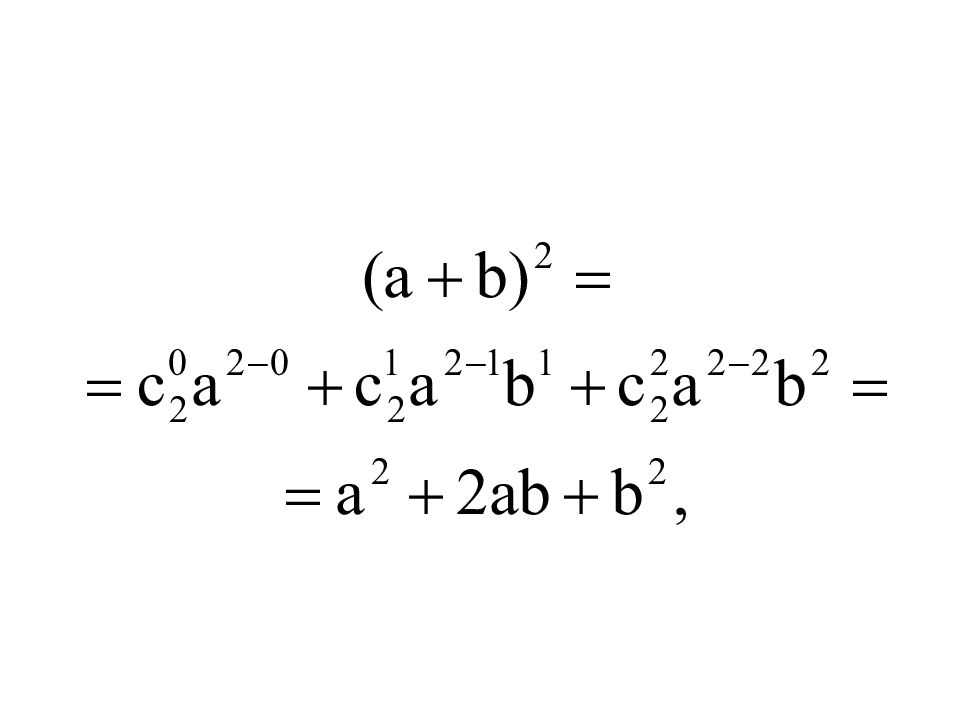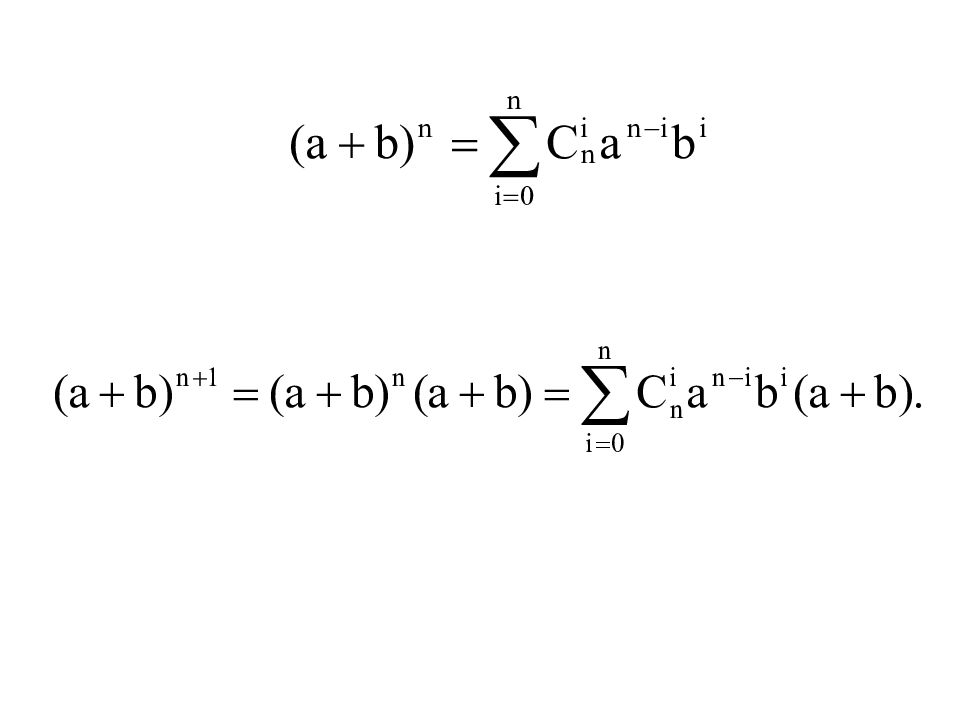Первый слайд презентации: Тема2 Элементы комбинаторики
Слайд 3
Раздел дискретной математики, занимающийся подсчетом и перечислением элементов в конечных множествах – комбинаторика или комбинаторный анализ.
Слайд 6
Вычисления на дискретных конечных математических структурах часто называют комбинаторными вычислениями. «Проклятие размерности»
Слайд 7
Основополагающие правила комбинаторики –суммы и произведения Понятие выборки (комбинации)
Слайд 8: Размещения с повторениями
Слайд 13: Пример сочетаний без повторений
Определить число двухэлементных подмножеств множества, состоящего из трех элементов.
Слайд 15: 1. Сочетания с повторениями
В ряде комбинаторных задач требуется подсчитывать число различных составов векторов длины k из n элементного множества. Такие векторы-составы называются сочетаниями с повторениями из n элементов по k. Например, требуется составить бригады ССО из 3 студентов 2 специальностей (каменщики и плотники) и определить количество таких бригад.
Слайд 16
Каждая бригада задается вектором длины 3 из 2 элементов, порядок компонент которого роли не играет. ( m 1, m 1, m 1),( m 1, m 2, m 2), ( m 1, m 1, m 2),( m 2, m 2, m 2) Состав (3,0);(1,2);(2,1);(0,3)
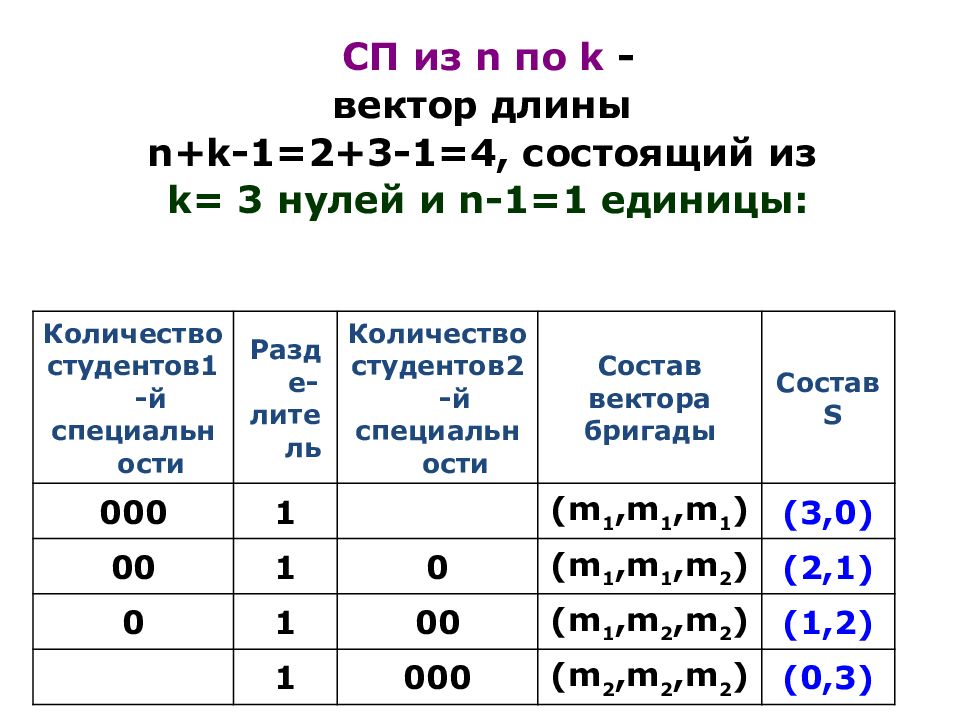
Слайд 17
СП из n по k - вектор длины n+k-1=2+3-1=4, состоящий из k= 3 нулей и n-1=1 единицы: Количество студентов1-й специальности Разде- литель Количество студентов2-й специальности Состав вектора бригады Состав S 000 1 (m 1,m 1,m 1 ) (3, 0) 00 1 0 (m 1,m 1,m 2 ) ( 2,1 ) 0 1 00 (m 1,m 2,m 2 ) ( 1,2 ) 1 000 (m 2,m 2,m 2 ) ( 0,3 )
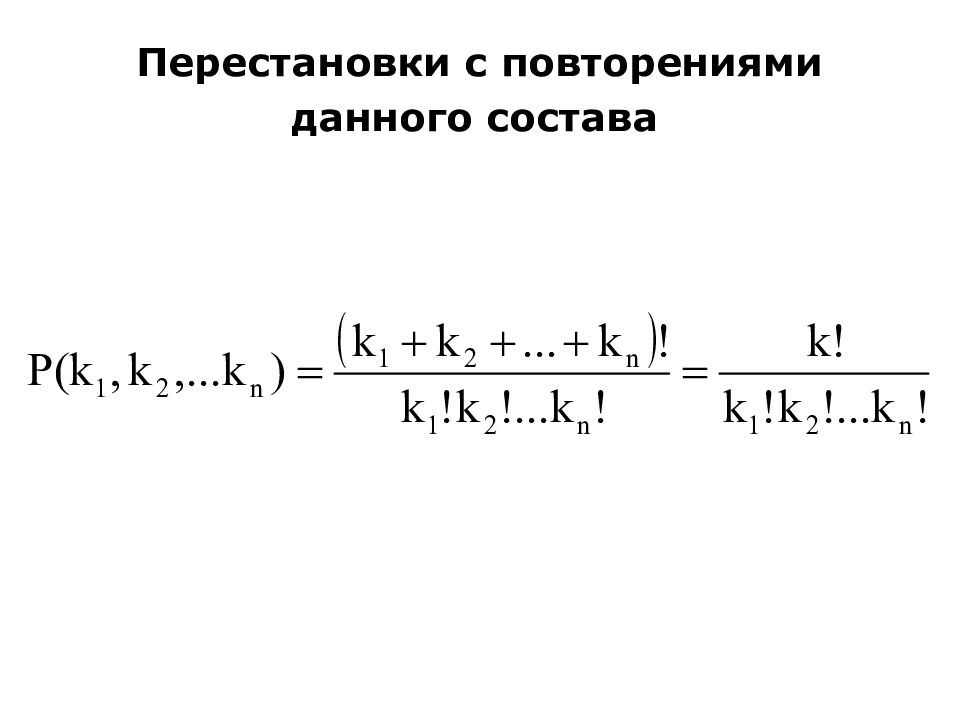
Слайд 19: Формула числа сочетаний с повторениями
Это перестановки с повторениями данного состава (вектор имеет одну единицу и три нуля):
Слайд 21
Пример: определить количество ударных войсковых группировок из 6 бригад 4 типов; Это сочетания с повторениями из 4-х элементов по 6:
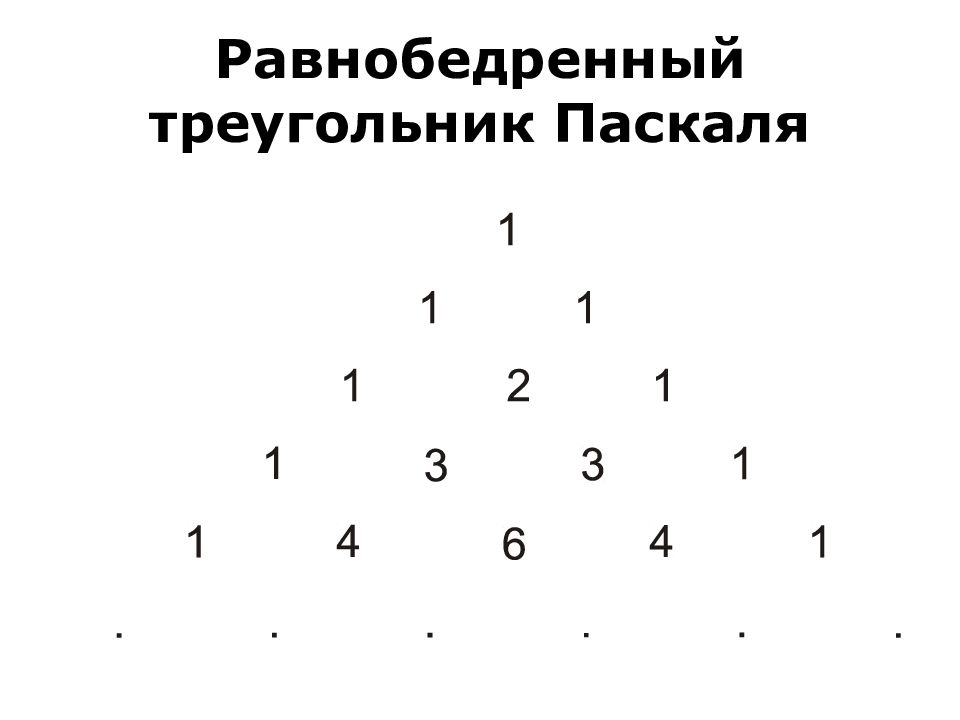
Слайд 22: 2. Треугольник Паскаля
Сочетаниями без повторений занимался еще великий Паскаль. Он предложил специальную таблицу значений сочетаний без повторений. Значения представлены в таблице, которая называется треугольником Паскаля.
Слайд 23
Блез Паскаль (фр. Blaise Pascal, 19 июня 1623 —19 августа 1662 ) — французский математик, физик, литератор и философ. Классик французской литературы, один из основателей математического анализа, теории вероятностей и проективной геометрии, создатель первых образцов счётной техники.
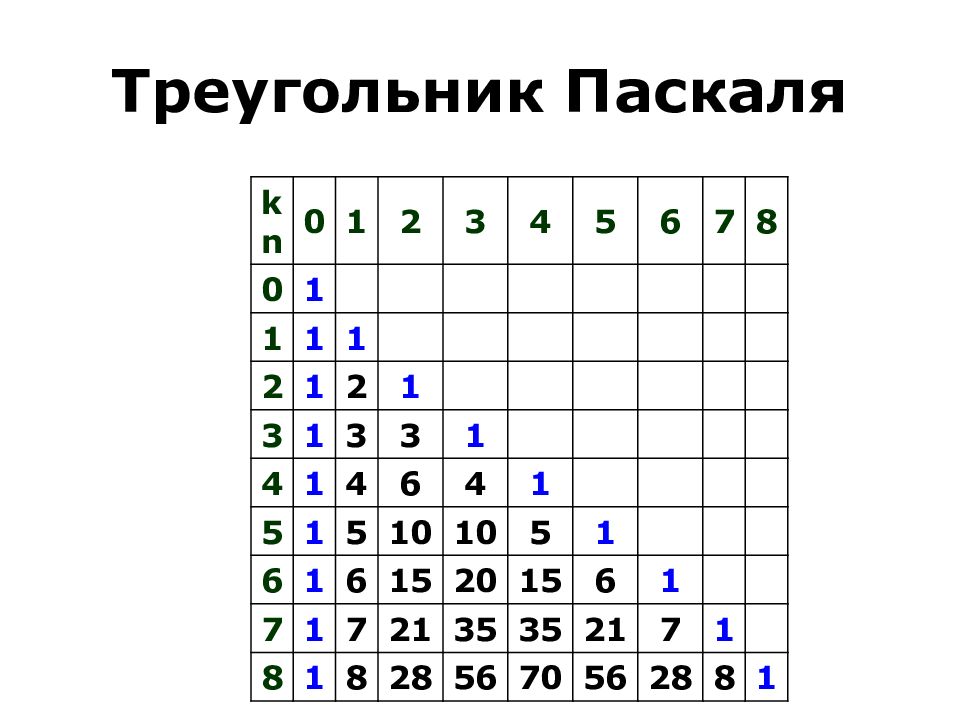
Слайд 24: Треугольник Паскаля
k n 0 1 2 3 4 5 6 7 8 0 1 1 1 1 2 1 2 1 3 1 3 3 1 4 1 4 6 4 1 5 1 5 10 10 5 1 6 1 6 15 20 15 6 1 7 1 7 21 35 35 21 7 1 8 1 8 28 56 70 56 28 8 1
Слайд 25
Заметим, что Этот треугольник удивительно красив своей математической красотой, и в его числах можно при желании отыскать различные закономерности.
Слайд 31: 3. Бином Ньютона
Слайд 32: Сэр Исаак Ньютон (англ. Sir Isaac Newton, 4 января 1643 — 31 марта 1727 по григорианскому календарю)
Слайд 35: Докажем формулу бинома Ньютона по индукции
1) базис индукции – доказательство того, что формула верна для конкретного n, например, для n =1.
Слайд 36
2) индукционный шаг. Предполагая, что формула верна для некоторого n, убеждаются, что тогда она верна и для n +1. 3) при истинности шагов 1 и 2 заключают, что формула верна для любого n.
Слайд 37: Приступим к индукционному шагу
Возьмем выражение и получим из него выражение для n +1.
Слайд 40
Для выполнения индукционного шага необходимо показать, что это выражение равно выражению: Рассмотрим подвыражение и заменим i на i -1.
Слайд 42
Это позволит вынести за скобку Но тогда в не учтен n -й член подвыражения
Слайд 44
Нетрудно видеть, что можно заменить на кроме того, мы уже доказали, что поэтому: что, очевидно, равно выражению
Слайд 45: По индукции получаем, что формула бинома Ньютона верна для любого n. Следствие №1
Слайд 47: Производящие функции
На использовании бинома Ньютона основано понятие производящей функции – функции, позволяющей получать комбинаторные числа без вычисления факториала: Здесь функция, производящая биномиальные коэффициенты.
Слайд 48: Функция, производящая биномиальные коэффициенты
При n =1 получаем 1+ x, т.е (коэффициент перед 1), (коэффициент перед x ). При n =2 получаем т.е
Последний слайд презентации: Тема2 Элементы комбинаторики: Решение комбинаторных уравнений
В комбинаторике тоже могут решаться уравнения, особенностью которых является то, что неизвестная принадлежит множеству натуральных чисел Например, уравнения вида x N, где N – множество натуральных чисел.