Первый слайд презентации: Комбинаторика
Слайд 2
Комбинаторика представляет собой область математики, занимающейся подсчётом элементов конечных множеств. Изучаются вопросы о том, сколько различных комбинаций можно составить из заданных элементов (объектов) с учетом тех или иных условий. Общие задачи подсчета связаны с выборкой (расстановкой, комбинацией, сочетанием) некоторого числа элементов из заданного базисного множества. Такие задачи полезно делить на типы в зависимости от того, как выбираются элементы: с повторением или без повторений, с учетом порядка выбора или без оного.
Слайд 3: История
Появление комбинаторики как самостоятельной ветви математики — Г.В. Лейбниц (1666 — «Об искусстве комбинаторики») Никколо Тарталья (1499 – 1557) Джероламо Кардано (1501 – 1576) Галилео Галилей (1564 – 1642) Блез Паскаль (1623 – 1662) Якоб Бернулли (1654 – 1705) Пьер Ферма (1601 – 1665) Леонард Эйлер (1707 – 1783)
Слайд 4: Правила суммы и произведения
Задача 1. В небольшой кондитерской к концу рабочего дня осталось несколько пирожных: четыре ванильных, два шоколадных и три фруктовых. Один покупатель собирается купить пирожное перед закрытием кондитерской. Сколькими способами покупатель может выбрать пирожное? Задача 2. Необходимо выбрать смешанную команду, которая будет представлять местный теннисный клуб на соревнованиях. В спортивном клубе состоят 6 женщин и 9 мужчин. Сколько различных пар можно выбрать для участия в соревнованиях? Задача 3. Сколько трехзначных чисел начинаются с 3 или 4?
Слайд 5
Правило суммы гласит, что если А и В — несвязанные события, и существует n 1 возможных исходов события А, и n 2 возможных исходов события В, то возможное число исходов события «А или В» равно сумме n 1 + n 2. Правило произведения утверждает, что если дана последовательность k событий с n 1 возможными исходами первого, n 2 —второго, и т.д., вплоть до n k возможных исходов последнего, то общее число исходов последовательности k событий равно произведению n 1 * n 2 *…* n k.
Слайд 6
Правило суммы, по существу, — частный случай формулы включений и исключений. Действительно, если рассматривать А и В как множества исходов, то |А| = n 1, |В| = n 2 ; а поскольку события А и В не связаны друг с другом, то можно считать, что соответствующие множества не пересекаются. Тогда, по формуле включений и исключений, |А В| = | А| + |В|, т.е. множество A В содержит n 1 + n 2 элементов. Это означает, что существует n 1 + n 2 возможных исхода события «А или В». Правило произведения тоже можно сформулировать на языке теории множеств. Пусть А 1 обозначает множество n 1 исходов первого события, А 2 — множество n 2 исходов второго, и т. д. Тогда любую последовательность к событий можно рассматривать как элемент декартова произведения А 1 А 2 … А k, чья мощность равна |А 1 | |А 2 | … |А k |
Слайд 7
Решение 3 задачи. Будем использовать как правило суммы, так и произведения. Трехзначные числа естественным образом разбиваются на два непересекающихся класса. К одному из них относятся числа, начинающиеся с 3, а ко второму — с 4. Для подсчета чисел в первом классе заметим, что существует один возможный исход для первой цифры (она должна быть равна 3), 10 исходов для второй и 10 исходов для последней цифры. По правилу произведения получаем, что всего чисел в первом классе насчитывается ровно 1 10 10 = 100. Аналогично можно подсчитать количество чисел во втором классе. Оно тоже равно 100. Наконец, по правилу суммы получаем, что существует 100 + 100 = 200 трехзначных чисел, начинающихся с 3 или 4.
Слайд 8: Пример
Я хочу взять с собой для ланча два фрукта. У меня есть три банана, четыре яблока и две груши. Сколькими способами я могу выбрать два фрукта разного вида из имеющихся у меня? Решение. Если я собираюсь взять один из трех бананов и одно из четырех яблок, то сделать я это могу 3 4 = 12 различными способами. Банан и грушу я могу взять 3 2 = 6 возможными способами. Наконец, грушу и яблоко можно выбрать 4 2 = 8 различными способами. Поскольку все три множества возможностей различны, то всего количество способов, которыми можно выбрать два фрукта, равно 12 + 6 + 8 = 26.
Слайд 9: Пример
Государственный регистрационный знак легкового автомобиля состоит из трех цифр и трех букв русского алфавита (не считая кода города). Будем считать, что в номере можно задействовать любую последовательность букв и цифр. Сколько различных автомобильных номеров может выдать ГИБДД? Решение. Каждую из трех букв номера можно выбрать из 33 букв алфавита. По правилу произведения число различных последовательностей из трех букв равно 33 33 33 = 35 937. Аналогично, число последовательностей трех цифр равно 10 10 10 = 1000. Наконец, поскольку каждый из автомобильных номеров состоит из трех букв и трех цифр, правило произведения дает искомый ответ: 35937000 различных автомобильных номеров может выдать ГИБДД.
Слайд 10: Комбинаторные формулы
Допустим, что ребенку предложили мешок с конфетами трех наименований: «Мишка на севере» (А), «А ну-ка отними» (В) и «Золотой петушок» (С). Сколькими способами ребенок может выбрать две конфеты из мешка? Требуемые уточнения, можно ли брать конфеты одного наименования или нет. Имеет ли значение порядок выбора? Четыре разных уточнения формулировки. 1. Повторения разрешены и порядок выбора существенен. В этом случае у нас есть 9 возможностей: АА, АВ, АС, ВА, ВВ, ВС, СА, СВ и СС. 2. Запрещено брать конфеты одного наименования, но порядок существенен. В этой ситуации — 6 случаев: АВ, АС, ВА, ВС, СА и СВ. 3. Повторения разрешены, но порядок выбора не имеет значения. Тогда ответ — тоже 6 возможностей: АА, АВ, АС, ВВ, ВС и СС. 4. И, наконец, если нельзя брать одинаковые конфеты, а порядок не имеет значения, то у ребенка есть только три варианта выбора: АВ, АС и ВС.
Слайд 11: Уточнения формулировок
Предположим, что мы берем элементы х 1, x 2, …, х k из множества X мощности n. Каждый такой набор принято называть выборкой объема k из n элементов или, иначе, ( n, k )-выборкой. Выборка называется упорядоченной, если порядок следования элементов в ней задан. При этом две упорядоченные выборки, различающиеся лишь порядком следования элементов, считаются разными. Если же порядок следования элементов в выборке не имеет значения, то выборка называется неупорядоченной.
Слайд 12
• ( n, k )- размещением с повторениями называется упорядоченная ( n, k )-выборка, элементы в которой могут повторяться; • ( n, k ) -размещением без повторений называется упорядоченная ( n, k )-выборка, элементам в которой повторяться запрещено; • неупорядоченная ( n, k )-выборка с повторяющимися элементами называется ( n, k )- сочетанием с повторениями ; • неупорядоченная ( n, k )-выборка без повторяющихся элементов называется ( n, k )- сочетанием без повторений.
На первое место выборки мы можем поставить любой из n элементов множества. Поскольку повторения разрешены, то на второе место мы опять можем поставить любой элемент из этого же множества, и т. д. Поскольку у нас k мест в выборке, то опираясь на правило произведения, получаем, что число всех ( n, k )-размещений с повторениями равно n k.
Слайд 14: Пример
Целые числа в компьютере представляются строчкой из N двоичных знаков. Первый из них отведен на знак (+ или –), а остальные N — 1 отвечают за модуль целого числа. Сколько различных целых чисел может использовать компьютер? Решение. Двоичная цифра — это 0 или 1. Для записи числа используется N таких цифр. Заметим, что двоичные строки, представляющие числа, могут иметь повторяющиеся цифры, и порядок их следования, естественно, существенен для данной задачи. Поэтому мы имеем дело с (2, N )-размещениями с повторениями. По выведенной формуле получаем, что общее количество таких строк равно 2 N. Практически всегда различные размещения изображают различные числа, за исключением двух строк: -000000…00 и + 000000…00, которые изображают 0. Стало быть, компьютер может оперировать (2 N — 1) целыми числами.
Слайд 15: ( n, k )-размещения без повторений P ( n, k )
На первое место выборки мы можем поставить любой из n элементов, для второго места мы можем выбрать любой из ( n – 1) оставшихся элементов. На третье — из ( n — 2) и так далее, вплоть до k -го места, куда можно написать любой из ( n — k +1) элементов. Теперь для окончательного ответа нам нужно применить правило произведения. Имеем Р ( n, k ) = n ( n – 1)( n – 2) … ( n – k +1). Р ( n, k ) = n !/( n – k )!
Слайд 16: Пример
Сколько различных четырехбуквенных «слов» можно написать, используя буквы: а, с, п, о, и, е, если под «словом» мы будем понимать любую последовательность неповторяющихся букв, даже если эта последовательность не несет в себе никакого смысла. Решение. Как договорились, под «словом» мы понимаем любую последовательность четырех разных букв, которые можно выбрать из шести данных. Значит мы имеем дело с подсчетом числа размещений без повторений Р (6, 4). Р (6, 4) = 6!/(6 –4)! = 360.
Слайд 17: Сочетания без повторений С ( n, k ) ( порядок не существенен, повторы запрещены)
Число всех ( n, k )- размещений без повторений равно Р ( n, k ) = n !/( n – k )!. Поскольку размещение без повторений отличается от сочетания без повторений наличием порядка, то число Р ( n, k ), естественно больше, чем С ( n, k ). Пусть n = 4, а k = 3. Зафиксируем множество А = {1, 2, 3, 4}, откуда мы будем брать элементы. Каждое (4, 3)-сочетание без повторений — это выбор последовательности трех разных цифр из четырех данных, причем порядок, в котором будут идти выбранные цифры, значения не имеет. Например, подмножество {1, 2, 3} является (4, 3)-сочетанием без повторений. Перемешав цифры в выбранном подмножестве {2, 1, 3}, мы получим то же самое сочетание (порядок не важен), но совершенно другое размещение (порядок существенен). Так сколько же различных размещений можно получить из одного сочетания? В данном конкретном случае ( n = 4, k = 3) ответ легко получить, перечислив вручную все варианты. Дано ( n, k )-сочетание без повторений, т. е. выбрано подмножество В А, где |В| = k и |А| = n. Сколько из него можно получить разных ( n, k )-размещений без повторений? Фактически, нам нужно подсчитать количество ( k, k )-размещений без повторений! Р ( k, k ) = k !/( k – k )! = k ! Таким образом, на каждое ( n, k )-сочетание без повторений приходится k ! различных ( n, k )-размещений без повторений. Стало быть, С ( n, k ) = Р ( n, k ) / k ! = n !/(( n – k )! k !)
Слайд 18: Пример
Меню в китайском ресторане дает Вам возможность выбрать ровно три из семи главных блюд. Сколькими способами Вы можете сделать заказ?
Слайд 19: Сочетания с повторениями
Предположим, например, что мы сделали выборку, состоящую из пяти букв, каждая из которых может быть одной из а, б и в. Выборку, состоящую из двух «а», одной «б» и двух «в», можно записать как аа|б|вв, а выборка из одной буквы «а» и четырех букв «в» будет выглядеть так: a||вввв. Договоримся, что слева от первой метки либо стоят буквы «а», либо ничего, справа от второй метки — либо «в», либо ничего, а буквы «б», если они присутствуют в выборке, стоят между метками. Таким образом, можно считать, что мы всегда смотрим на семь ячеек (пять букв и две метки), причем различные выборки будут отличаться ячейками, в которых стоят метки. Первую метку можно поставить в любую из 7 ячеек, а вторую — в любую из 6. Это дает нам 7 • 6 возможностей. Поменяв расставленные метки местами, мы получим то же самое заполнение ячеек. Итак, количество способов равно 7 6/2. Возвращаясь к общему случаю ( n – k )-сочетаний без повторений заметим, что нам потребуется n – 1 метка и k объектов. Т. о., будет ( n — 1) + k ячеек для заполнения. Значит, число ( n – k )-сочетаний без повторений совпадает с количеством способов размещения ( n – 1) метки в ( n + k – 1) ячейку. Итак, общее число ( n – k )-сочетаний без повторений равно С ( n + k – 1, n – 1) = ( n + k – 1)!/( k ! ( n – 1)!)
Слайд 20: Пример
Сколько различных вариантов можно получить, бросая пять игральных костей? Решение. На каждой из костей может выпасть от одного до шести очков, т. е. каждая кость дает шесть вариантов. Если бросили пять костей, то каждый вариант можно рассматривать как неупорядоченный набор пяти объектов (для каждого из которых есть 6 возможностей) с повторениями, т. е. (6, 5)-сочетание с повторениями. Согласно общей формуле, общее число исходов равно 252.
Слайд 22: Пример
В Спортлото случайным образом выбирается шесть разных номеров из первых 49 натуральных чисел. Любой, кто угадает все шесть выпавших номеров, выиграет главный приз, который может достигать миллион рублей. Подсчитаем шансы выигрыша главного приза. Шестерка выигрышных номеров — это неупорядоченная выборка шести чисел из 49 возможных. Поскольку общее количество (49, 6)-сочетаний без повторений равно 49!/((49-6)!6!) =13 983 816, то шансов выиграть практически нет: 1 из 13 983 816.
Слайд 23
Тем, кто угадал пять, четыре или три номера, тоже присуждается приз. Будем считать, что величина денежного приза зависит от числа проданных билетов. Допустим, каждый билет стоит 10 рублей, и любой, кто угадает ровно три (и не больше) выигрышных номера, автоматически выигрывает 100 рублей. Подсчитаем вероятность выигрыша 100 руб. Можно рассматривать шесть номеров как объединение двух несвязанных событий: выборка трех правильных номеров и трех неверных. Существует С(6,3) возможностей назвать три из шести правильных номеров и С(43,3) — возможностей неудачного выбора. Тогда общее число комбинаций, выигрывающих 100 рублей, равно С(6,3) С(43,3) = 246 820 Вероятность выигрыша — это доля удачно заполненных карточек ко всем возможным заполнениям, т. е. 246 820/13983816 1.57 0,018
Слайд 24: Бином Ньютона
Числа С ( n, k ) возникают как коэффициенты при раскрытии скобок в биноме ( a + b ) n. Например, ( a + b ) 3 = ( a + b )( a + b )( a + b ) = ааа + aab + aba + abb + baa + bab + bba + bbb = = a 3 + 3 a 2 b + 3 ab 2 + b 3 Каждое из восьми слагаемых, стоящих во второй строке наших преобразований, получается при умножении трех переменных, выбираемых по одной из каждой скобки. Мы видим, в частности, что ровно три слагаемых содержат одну переменную а и две b. Это происходит потому, что у нас есть С(3, 2) = 3 способа выбора двух скобок из трех, откуда мы возьмем переменную b (а из оставшейся берем а ). Аналогично получаются и остальные коэффициенты этого выражения: С(3, 0) = 1, С(3, 1) = 3, С(3, 2) = 3 и С(3, 3) = 1. Иначе говоря, существует единственная возможность не сделать никакого выбора из конечного множества объектов. В общем случае, раскрывая скобки в биноме ( a + b ) n, мы будем получать члены вида а n - k b k (где k принимает каждое из значений от 0 до n ) при перемножении символов b, взятых из k скобок, и а, взятых из оставшихся ( n – k ) скобок. Так как есть ровно С ( n, k ) способов выбора k скобок из n, то у нас будет в точности С ( n, k ) членов вида а n - k b k при k = 0, 1,..., n. Следовательно, ( a + b ) n = C ( n, 0) a n + C ( n, l ) a n - l b + C ( n, 2) a n -2 b 2 + ••• + C ( n, n ) b n. Эта формула называется биномом Ньютона.
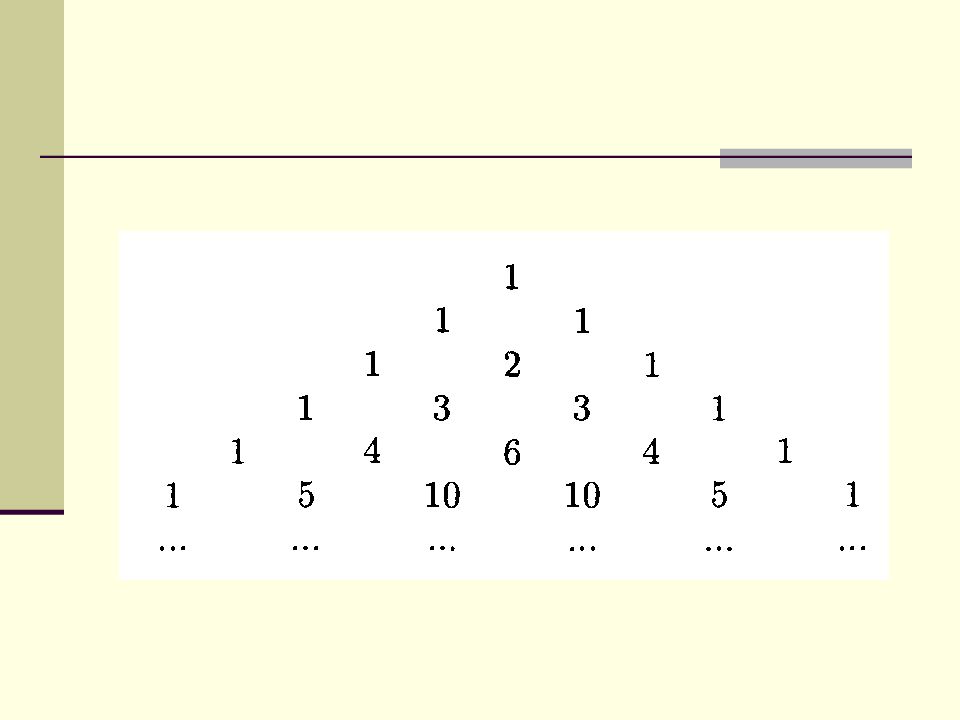
Слайд 27: Треугольник Паскаля. Закономерности
Так как С ( n, 0) = С ( n, n ) = 1, на внешних сторонах треугольника Паскаля всегда стоят единицы. Симметрия относительно вертикальной высоты треугольника следует из тождества: С ( n, k ) = С ( n, n – k ). Сложив два последовательных числа, стоящих в строке треугольника, мы получим число из следующей строки, которое стоит между двумя сложенными. Это свойство известно как формула Паскаля: С ( п – 1, k – 1) + С ( п – 1, k ) = С ( п, k )
Слайд 28: Теорема о перестановках
Найдем количество перестановок букв в слове «КОЛОБОК». Оно состоит из семи букв, которые можно переставить 7! способами. Однако в нем есть три буквы «О» и две буквы «К». Поэтому меняя местами буквы «О» или переставляя буквы «К», мы не получим новых «слов». Так как количество перестановок трех элементов равно 3!, а двух — 2!, то мы можем получить всего 7! /(3!2!) = = 420 разных «слов» из слова «КОЛОБОК». В общей ситуации справедлива следующая теорема о перестановках. Теорема. Существует n ! / ( n 1 ! n 2 ! n r !) различных перестановок n объектов, n 1 из которых относятся к типу 1, n 2 — к типу 2, и т. д. вплоть до n r объектов типа r.
Слайд 29: Пример
Сколькими способами можно распределить 15 студентов по трем учебным группам по пять студентов в каждой? Решение. У нас есть 15 объектов, которые нужно организовать в три группы по пять. Это можно сделать 15 / (5! 5! 5!) = 68 796 различными способами. Коэффициенты n ! / ( n 1 ! n 2 ! n r !) носят название мультиномиальных.
Слайд 30: Комбинаторные задачи
Разбиение множества на два подмножества Дано множество. Требуется разделить все элементы на два непересекающихся подмножества. Сколько существует таких разбиений?
Слайд 31
Проще всего, если | A 1 | и | A 2 | заданы. Тогда число разбиений N равно Например, число разбиения множества десятичных цифр на два подмножества A 1 и A 2 при | A 1 | = 3 и | A 2 | = 7 равно
Последний слайд презентации: Комбинаторика
Этот же результат можно получить с применением формулы числа перестановок с повторениями. Для этого запишем в ряд элементы множества А и каждому элементу поставим в соответствие двоичный разряд, т.е. все разбиения закодируем двоичными кодами. Пусть нули обозначают элементы множества А 1, единицы – элементы множества А 2 : 0 1 2 3 4 5 6 7 8 9 0 0 0 1 1 1 1 1 1 1 В данном случае двоичному коду 0001111111 соответствует разбиение А 1 = {0, 1, 2 }; А 2 = {3, 4, 5, 6, 7, 8, 9}. Очевидно, что всякая перестановка нулей и единиц в двоичном числе определяет некоторое разбиение множества А. Например, числу 1011100111 соответствует разбиение вида А1 = {1, 5, 6}; А2 = {0, 2, 3, 4, 7, 8, 9}. По формуле числа перестановок из 10 элементов с повторениями получаем общее число разбиений: В общем случае имеем: