Гидрогазодинамика изучает закономерности течения жидкостей и газов и их силовое взаимодействие с омываемыми поврехностями Анализ течения жидкостей и газов проводится путем их моделирования. В общем случае моделью можно назвать имитацию изучаемого объекта по некоторой совокупности его свойств. В гидродинамике распространены модели: сплошности, несжимаемой идеальной
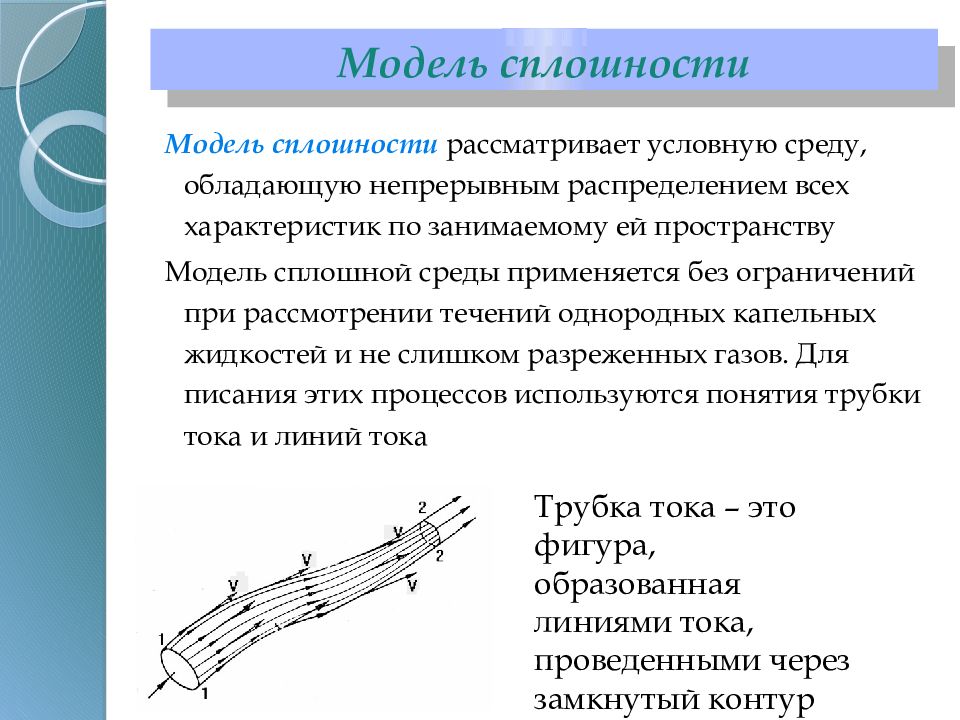
Модель сплошности рассматривает условную среду, обладающую непрерывным распределением всех характеристик по занимаемому ей пространству Модель сплошной среды применяется без ограничений при рассмотрении течений однородных капельных жидкостей и не слишком разреженных газов. Для писания этих процессов используются понятия трубки тока и линий тока Трубка тока – это фигура, образованная линиями тока, проведенными через замкнутый контур
Вязкостью называется свойство сред, оказывать сопротивление деформациям сдвига (сдвиговая вязкость) и объема (объемная или вторая вязкость). Со сдвиговой вязкостью связана текучесть – способность среды деформироваться под действием механических напряжений, количественно обратное вязкости. У газов и большинства жидкостей текучесть проявляется при любых напряжениях - динамический коэффициент вязкости, Пас ; зависит от физической природы среды, ее состояния и течения - кинематический коэффициент вязкости, м 2 /с Выбор терминологии связан с размерностью коэффициентов
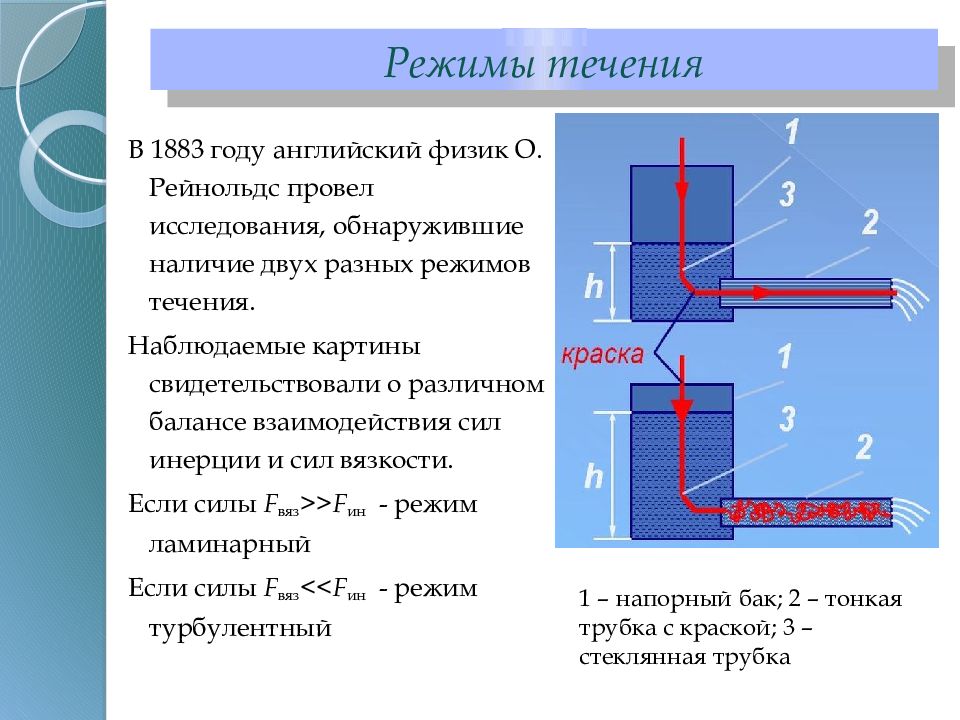
В 1883 году английский физик О. Рейнольдс провел исследования, обнаружившие наличие двух разных режимов течения. Наблюдаемые картины свидетельствовали о различном балансе взаимодействия сил инерции и сил вязкости. Если силы F вяз >> F ин - режим ламинарный Если силы F вяз << F ин - режим турбулентный 1 – напорный бак; 2 – тонкая трубка с краской; 3 – стеклянная трубка
ОСОБЕННОСТИ РЕЖИМОВ ТЕЧЕНИЯ: ( lamina – слой; turbulent – беспокойный, вихревой) Элементарные объемы среды в ламинарном течении двигаются параллельно друг другу, не перемешиваясь. Скорость и другие параметры течения – непрерывные функции координат и времени. В турбулентных потоках наблюдаются неупорядоченные изменения параметров потока и скорости. Таким образом, ламинарное течение может как стационарным, так и нестационарным. А турбулентное нестационарное в принципе. В ламинарных течениях перенос вещества, энергии между соседними слоями в потоке осуществляется за счет молекулярного механизма. В турбулентных течениях пульсационную составляющую движения рассматривают как аналог молекулярного хаотического движения в газах Режимы течения
Количественно режим течения вязких сред можно охарактеризовать величиной порядка отношения сил инерции к силам вязкости, называемой числом Рейнольдса Здесь - средняя расходная скорость, м/с; L – линейный масштаб, м; - кинематический коэффициент вязкости, м 2 /с Для случая течения вязкой среды в круглой трубе постоянного диаметра границей устойчивого ламинарного режима течения принято считать Re кр =2300 Развитое турбулентное течение в круглой трубе наблюдается при Re> 4000
В качестве линейного масштаба L при течении в трубопроводах используется гидравлический диаметр. S – площадь поперечного сечения, м 2 ; - смоченный периметр, м При течении в трубе диаметром d При течении по трубе квадратного сечения По трубе прямоугольного сечения При течении в кольцевом сечении канала (труба в трубе)
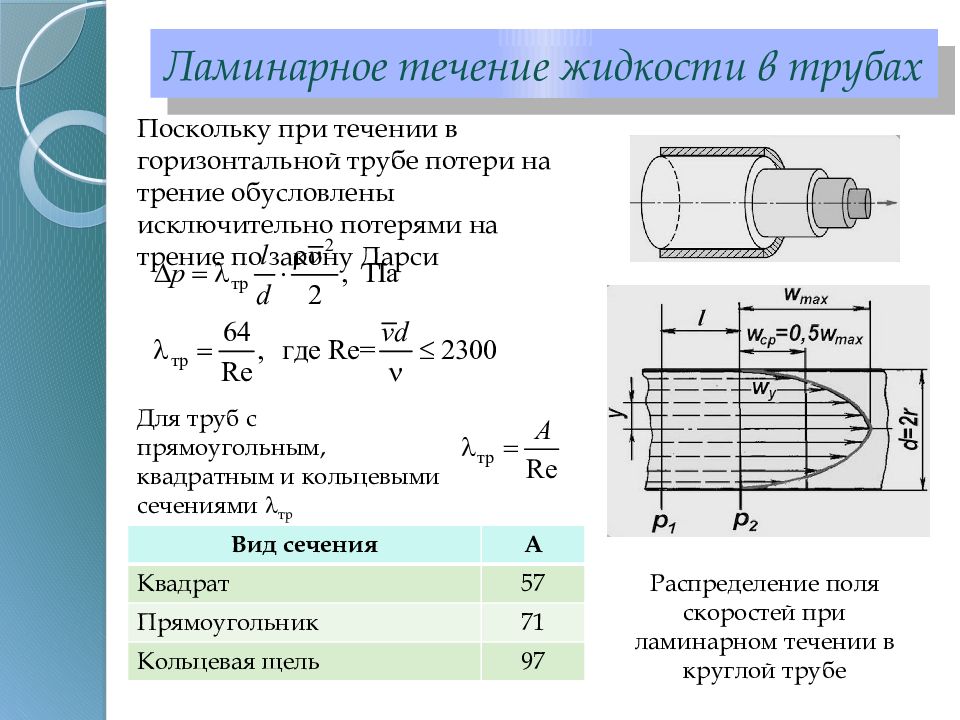
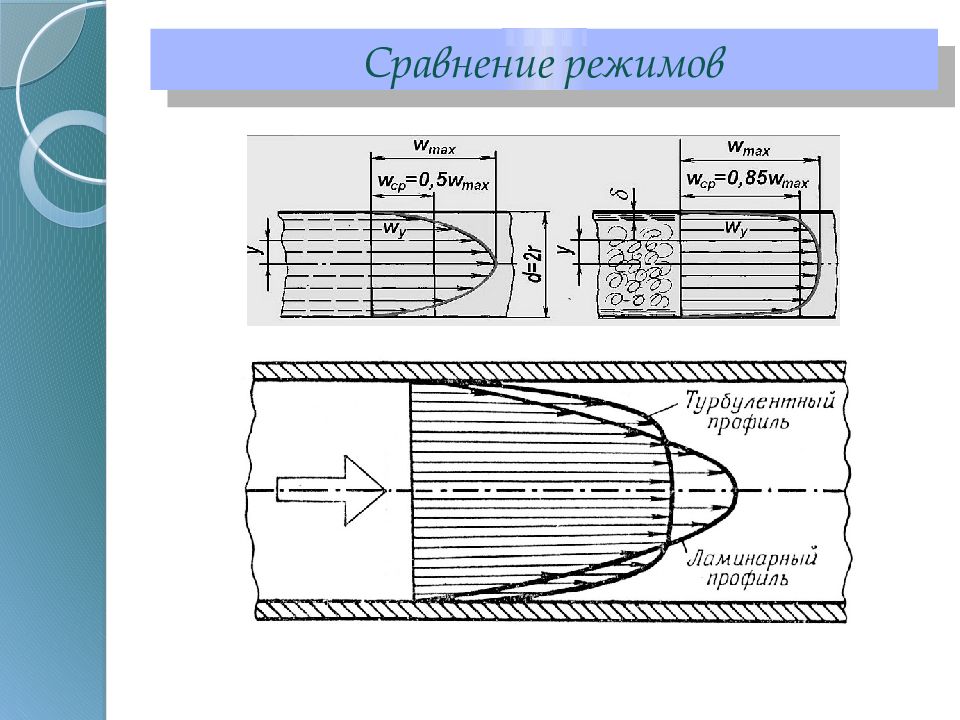
Распределение поля скоростей при ламинарном течении в круглой трубе Поскольку при течении в горизонтальной трубе потери на трение обусловлены исключительно потерями на трение по закону Дарси Для труб с прямоугольным, квадратным и кольцевыми сечениями тр Вид сечения А Квадрат 57 Прямоугольник 71 Кольцевая щель 97
Число Рейнольдса в этом случае определяется по гидравлическому диаметру. Для удобства практических расчетов потери на трение можно выразить через объемный и массовый расходы:
Профиль скоростей при турбулентном течении внутри трубопровода При установившемся турбулентном течении вязкой несжимаемой жидкости в горизонтальной трубе диаметра d реализуется распределение скоростей, при котором максимальная скорость достигается на оси трубы, а на стенках равна нулю (вследствие теории прилипания). В пределах пристенной зоны скорость распределяется по линейному закону. Эта зона называется вязкий подслой. За пределами вязкого подслоя находится турбулентное ядро потока.
С ростом числа Рейнольдса толщина вязкого подслоя уменьшается, что объясняет влияние шероховатости на сопротивления трения по длине трубопровода. Степень влияния шероховатости зависит от соотношения между абсолютной шероховатостью стенки трубы и толщиной вязкого подслоя и возрастает с ростом числа Рейнольдса. В зависимости от порядка этого соотношения различают три зоны сопротивления трения по длине трубопровода при турбулентном режиме течения Турбулентное течение жидкости в трубах Структура турбулентного потока вблизи шероховатой стенки при режимах : а – гладкостенного течения; б – проявление шероховатости
1. Зона гидравлически гладких труб. В пределах этой зоны выступы шероховатости полностью скрыты внутри вязкого подслоя экв < вязк и не взаимодействуют с турбулентными пульсациями. Сопротивление трения при этом зависит только от режима числа Рйенольдса тр = f (Re). Диапазон этой области по числу Рейнольдса 4000 <Re20d/ экв 2. Зона совместного влияния режима течения и шероховатости. Выступы шероховатости частично находятся в области турбулентного ядра потока и взаимодействуют с турбулентными пульсациями, что приводит к дополнительной диссипации механической энергии потока и росту сопротивления трения. Коэффициент потерь на трение тр = f (Re, экв / d), диапазон по числу Рейнольдса 20d/ экв <Re 50 0d/ экв 3. Зона развитой шероховатости или квадратичного закона сопротивления. Выступы шероховатости почти полностью находятся в пределах турбулентного ядра потока и сопротивление трения по длине трубопровода целиком определяется их взаимодействиями с турбулентными пульсациями. тр = f ( экв /d), Re> 50 0d/ экв Турбулентное течение жидкости в трубах
При стационарном течении в трубопроводе c непроницаемыми стенками массовый расход вещества G, кг/с, через поперечное произвольное сечение канала сохраняется. Отсюда можно оценить требуемый диаметр трубопровода для перекачивания заданного расхода среды. Для несжимаемой жидкости ( = const ) наряду с массовым сохраняется объемный расход среды Q, м 3 /с. Средние скорости жидкостей в трубопроводах обычно принимают в диапазоне (0,5 – 3) м/с; газов – (10-50) м/с
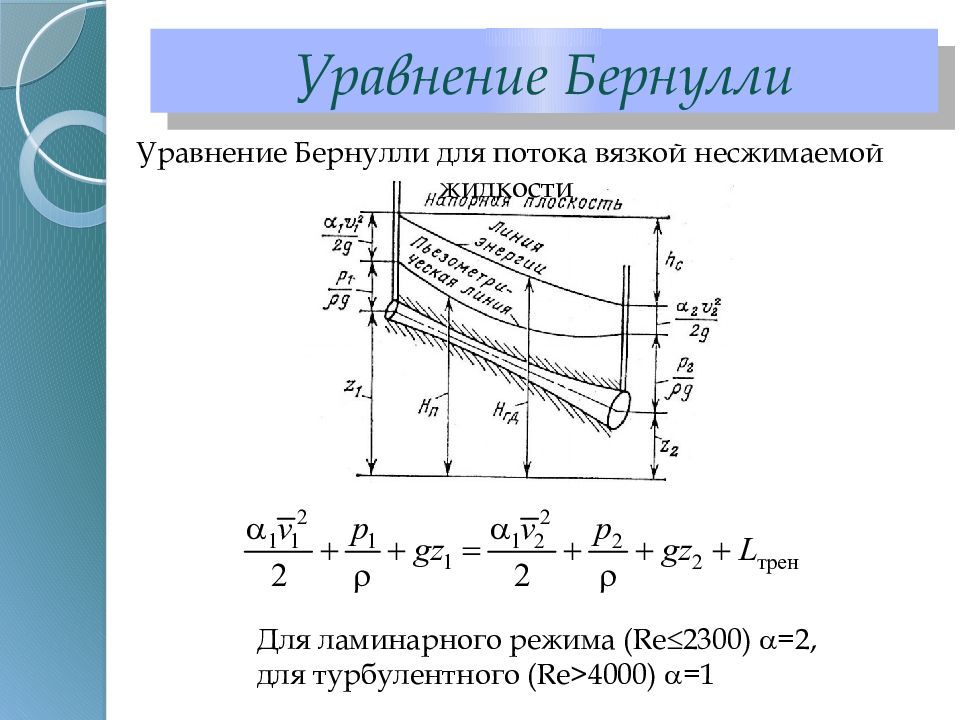
Уравнение Бернулли для потока вязкой несжимаемой жидкости Для ламинарного режима ( R е 2300) =2, для турбулентного ( Re>4000) =1
может быть представлено в виде суммы напоров (если разделить предыдущее уравнение на g ) Уравнение Бернулли Входящие в состав этого уравнения величины имеют размерность длины, м, и называются напорами динамический (статический) напор пьезометрический напор геометрический напор полный напор
Работа против сил трения L трен на участке трубопровода длиной L определяется как р трен – потери на трение по длине трубопровода; обусловлено вязким взаимодействием текущей жидкости со стенками трубопроводов р мест – потери на местных сопротивлениях; связаны с деформацией потока при течении с изменяющимися конфигурациями и размерами проходного сечения, направления течения жидкости Эти выражения являются основными для расчета трубопровода
Расчет потерь давления (напора) на трение по длине трубопровода проводят по формуле Дарси-Вейсбаха В области ламинарного режима течения тр зависит только от числа Рейнольдса ( Re= ( v d /) 2300) Для турбулентных режимов течения тр является функцией как числа Рейнольдса, так и относительной шероховатости стенок трубопровода экв = экв / d. Эквивалентная шероховатость экв средняя высота выступов шероховатости, зависит от материала трубопровода, технологи его изготовления, факторов эксплуатации; для расчетов определяется по справочным материалам. Потери на трение по длине трубопровода
В области Re> 4000 коэффициент потерь на трение рассчитывается по универсальной зависимости А.Д.Альтшуля При 4000 <Re<20d/ экв второе слагаемое существенно меньше первого и тр определяется по формуле Блазиуса Эта область называется областью гидравлически гладких труб, поскольку шероховатость стенок трубопровода в пределах этой зоны не оказывает существенного влияния на величину потерь на трение по длине. В этой области тр можно рассчитать также по формуле Прандтля Потери на трение по длине трубопровода
При Re>500d/ экв второе слагаемое по величине существенно превосходит первое, и коэффициент потерь на трение по длине тр определяется по формуле Эта область значений числа Рейнольдса называется зоной развитой шероховатости или зоной квадратичного закона сопротивления, поскольку в пределах этой зоны потери на трение по длине трубопровода пропорциональны квадрату средней скорости потока. Потери на трение по длине трубопровода
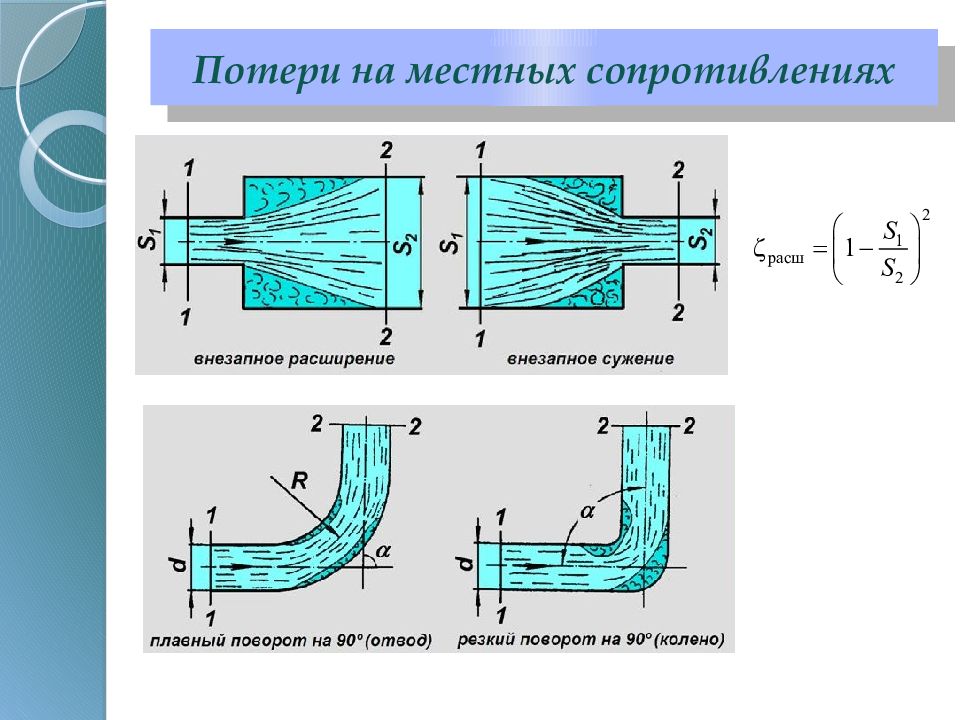
определяются по формуле Вейсбаха где мест – коэффициент местного сопротивления; его величина определяется только видом местного сопротивления. Потери на местных сопротивлениях можно условно разделить на группы: Потери, связанные с изменением сечения потока Потери, вызванные изменением направления потока Потери, вызванные движением жидкости через запорную и регулирующую арматуру различного типа Потери, возникающие из отделения одной части потока от другой или слияния потока Потери на местных сопротивлениях
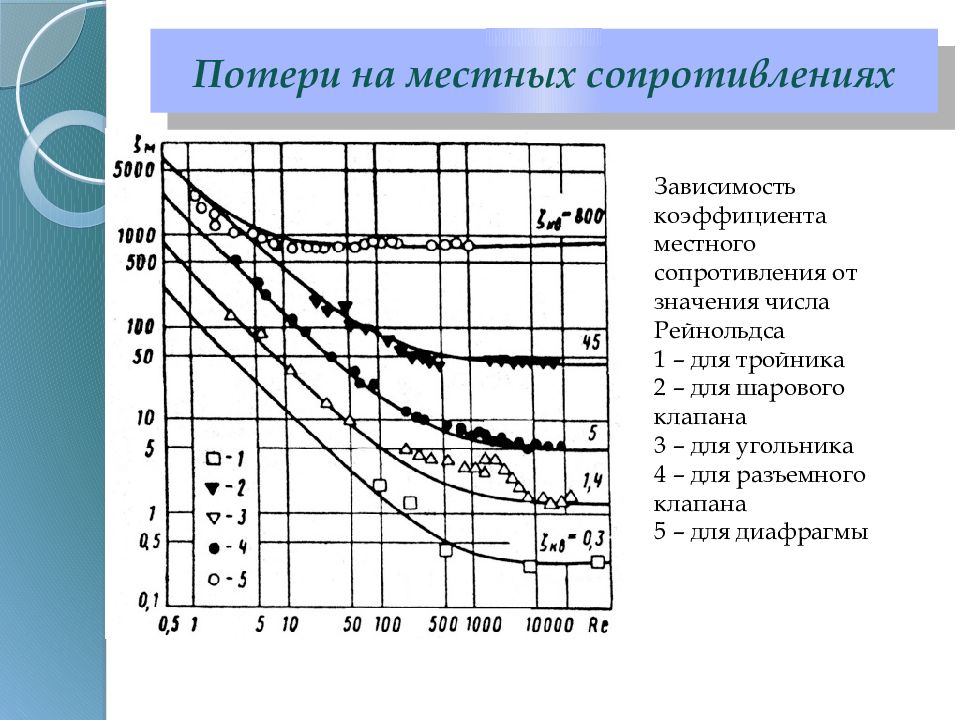
Зависимость коэффициента местного сопротивления от значения числа Рейнольдса 1 – для тройника 2 – для шарового клапана 3 – для угольника 4 – для разъемного клапана 5 – для диафрагмы
Трубопроводы подразделяются на простые и сложные. ПРОСТЫМ называется трубопровод, состоящий из одной линии труб с постоянным расходом, подающим жидкость из резервуара в атмосферу или другой резервуар. СЛОЖНЫЕ трубопроводы состоят из системы (сети) труб, подающих жидкость сразу в несколько точек. Сеть может быть разветвленной (разомкнутой или тупиковой) кольцевой (замкнутой) и включать как транзитные (без раздачи жидкости по пути), так и распределительные трубопрводы
В простом трубопроводе, транспортирующем несжимаемую жидкость, сохраняется Q=const. Суммарное сопротивление такого трубопровода определяется как сумма сопротивлений трения по длине трубопровода и на местных сопротивлениях (аналог электрической цепи из последовательно соединенных активных сопротивлений) Для простых трубопроводов местные потери напора выражают в виде эквивалентной длины L экв прямого участка трубопровода, сопротивление трения по длине которого, по величине равно рассматриваемым местным потерям
Введение понятия эквивалентной длины позволяет упростить гидравлические расчеты простых трубопроводов: при их приведении к истинной длине L добавляют установленную нормативами величину эквивалентной длины, учитывающей потери на местных сопротивлениях: L расч = L (1+ L экв / L ), и дальнейший расчет производят, предполагая, что потери напора обусловлены исключительно трением по длине L расч Рассмотрим некоторые примеры расчета простых трубопроводов Расчет простых трубопроводов
Рассмотрим трубопровод, подающий жидкость из колодца со всасывающий патрубок насоса. Высота расположения всасывающего патрубка над уровнем жидкости h. Давление на уровне жидкости в колодце равно атмосферному р 0, положение уровня в процессе работы насоса сохраняется неизменным. Покажем, что в этих условиях h высота ограниченная. Сечение 1 на уровне жидкости в колодце, а сечении 2 соответствует входу в насос. Запишем уравнение Бернулли Поскольку уровень жидкости в колодце по условию сохраняется, v 1 =0 ; z 2 - z 1 = h вс. Выразим h вс из уравнения с учетом исходных условий Пренебрегая потерями и динамическим напором жидкости во всасывающем патрубке и считая разряжение в сечении всасывания абсолютным ( р 2 =0) получим максимальную величину
производится по аналогии с расчетами электрических цепей на основании правил Кирхгоффа. В точке ветвления (пересечения нескольких трубопроводов) алгебраическая сумма объемных расходов жидкости равна нулю. При этом, расходы поступающие в точку ветвления имеет знак «+», а выходящие – «-». Сумма падений давления ( сопротивления), подсчитанных по замкнутому контуру (в кольцевом трубопроводе, например), равна нулю Расчет сложных трубопроводов
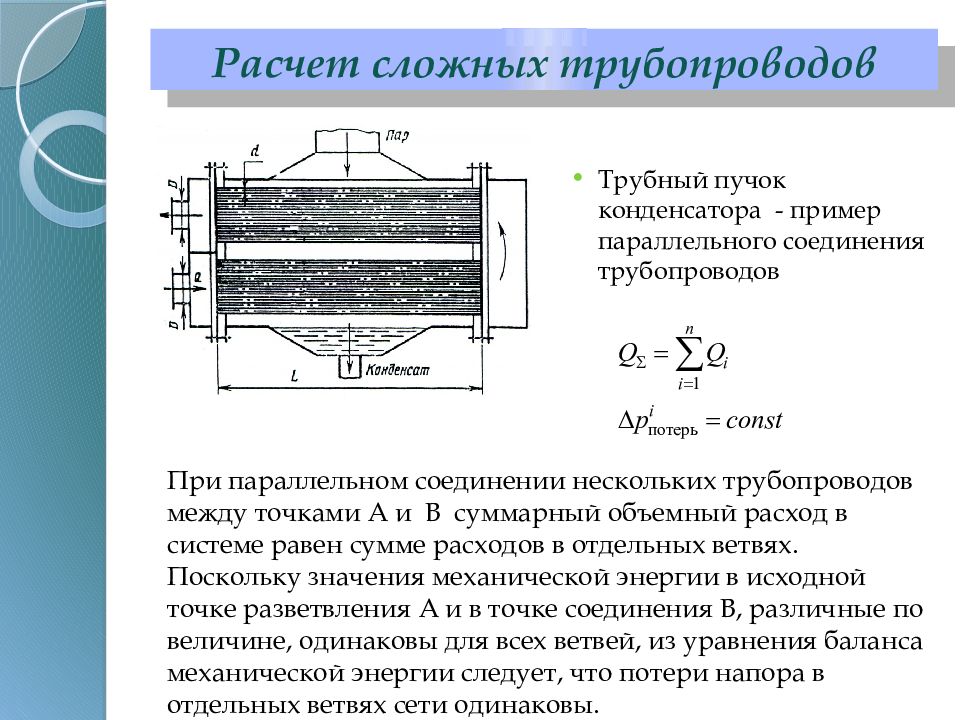
Трубный пучок конденсатора - пример параллельного соединения трубопроводов Расчет сложных трубопроводов При параллельном соединении нескольких трубопроводов между точками А и В суммарный объемный расход в системе равен сумме расходов в отдельных ветвях. Поскольку значения механической энергии в исходной точке разветвления А и в точке соединения В, различные по величине, одинаковы для всех ветвей, из уравнения баланса механической энергии следует, что потери напора в отдельных ветвях сети одинаковы.
Случай малых относительных перепадов давлений Если относительный перепад давления на концах трубопровода р / р 0,05 можно пренебречь сжимаемостью и считать плотность транспортируемого газа неизменной по длине трубопровода. В отличие от трубопроводов для перекачивания жидкостей в расчетах газопроводов пренебрегают изменением потенциальной энергии потока в поле сил тяжести вследствие малой плотности газа, а также кинетической энергией газа. Потери на трение по длине трубопровода определяются по закону Дарси. Плотность газа определяется по среднему давлению. Коэффициент потерь на трение определяется по формуле Альтшуля
Согласно нормативным документам Частные случаи: экв / d << 1922 d / Q экв / d >> 1922 d / Q р – мм.вод.ст.; экв, d – см; L – м; - м 2 /с; Q – м 3 /ч Особенности гидравлического расчета газопроводов
Случай больших относительных перепадов давлений Используя формулу Альтшуля для определения тр и размерную базу согласно нормативным документам ( р 1, р 2 – ат, L – км, d, экв – см, Q – м 3 /ч, - м 2 /с) Значения , Q, v предварительно приводят к нормальным условиям. Частные случаи: экв / d << 1922 d / Q экв / d >> 1922 d / Q Последнее выражение, действительное для квадратичной области сопротивления, применяется при больших скоростях ( > 50 м/с) Особенности гидравлического расчета газопроводов
При проектировании обычных паропроводов, как правило, назначают возможно меньший диаметр трубы, для уменьшения тепловых потерь. При этом реализуются высокие скорости движения пара (от 10 до 70 м/с), вследствие чего даже в коротких паропроводах возникают значительные потери напора. При перекачивании перегретого пара трубопровод тщательно изолируется, так что тепловые потери в окружающую среду незначительны. Тем не менее, температура пара снижается по длине паропровода в результате расширения пара; с другой стороны – температура пара возрастает из-за поступления тепла вследствие диссипации от потерь напора. В результате режим течения находится между изотермическим и адиабатическим. Поскольку температура пара изменяется по длине паропровода, меняются также динамическая вязкость , число Рейнольдса Re, коэффициент гидравлического трения тр. Поскольку скорости движения пара значительны, сопротивление относится чаще всего к квадратичной области. В паропроводах низкого давления (например, в отопительных системах) плотность пара и его температура в процессе движения изменяются так мало, что расчеты можно проводить по формулам для несжимаемых жидкостей.
