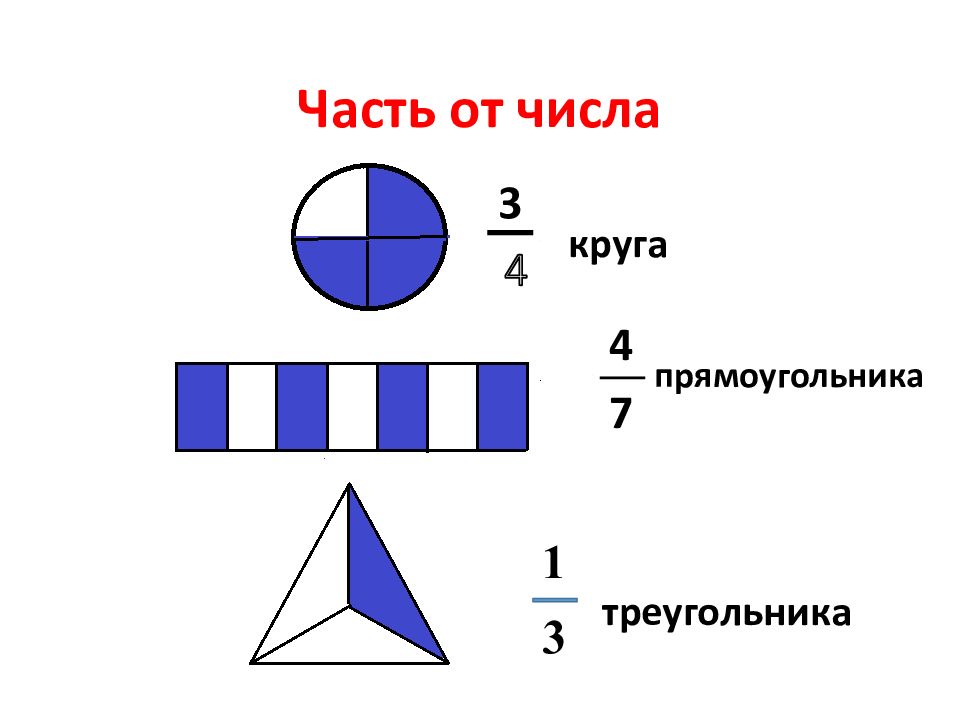
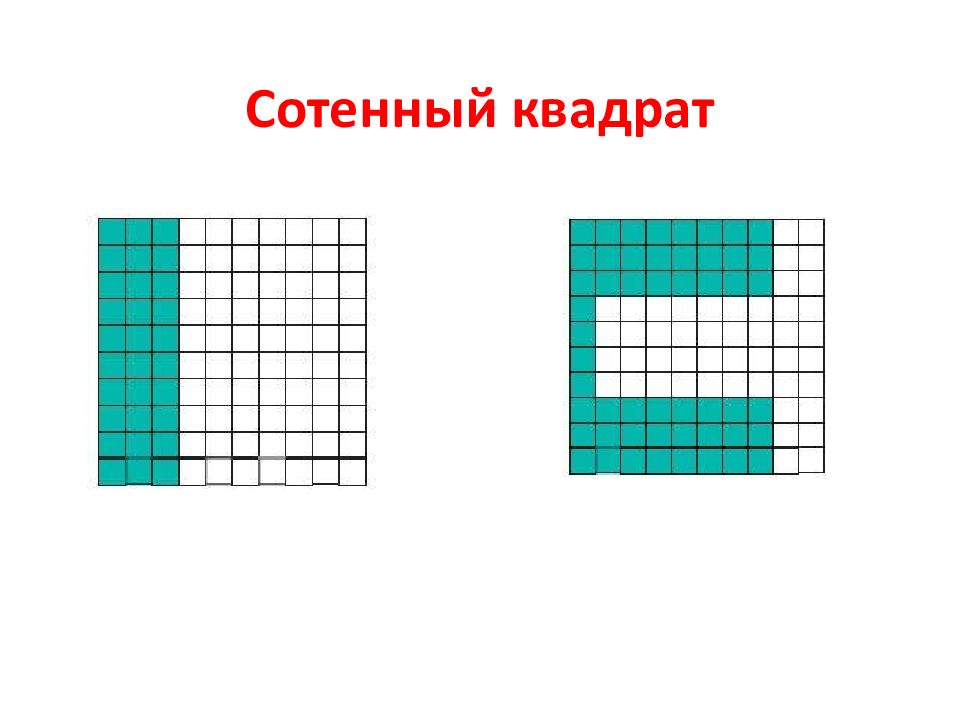
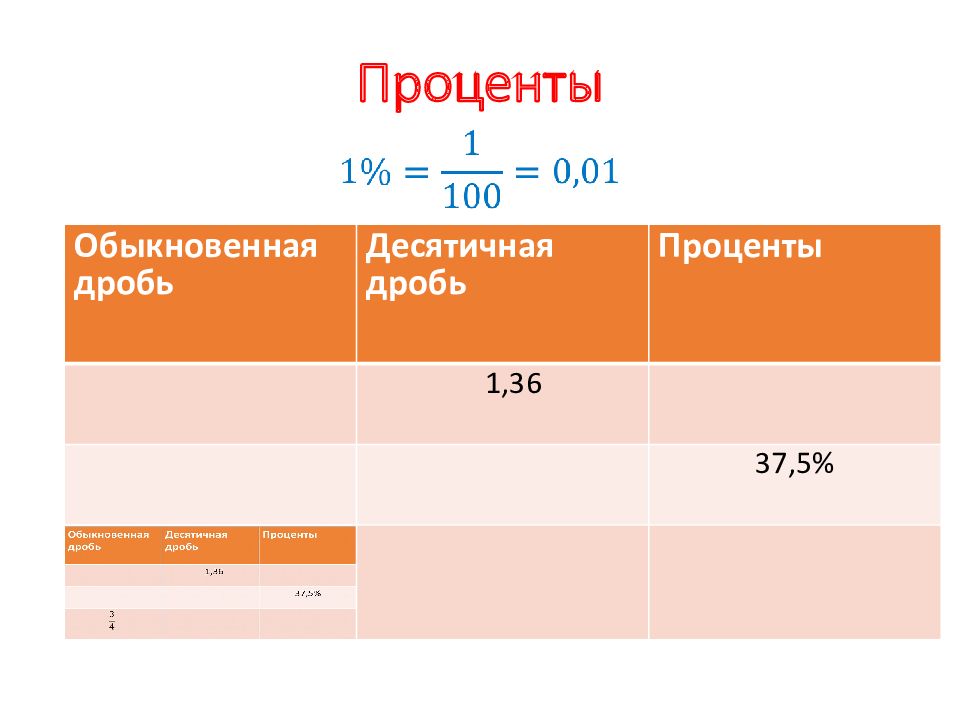
Слайд 4: Проценты
Обыкновенная дробь Десятичная дробь Проценты 1,36 37,5% Обыкновенная дробь Десятичная дробь Проценты 1,36 37,5%
Слайд 5: Задачи на модели «часть-целое»
Задача 1. Туристы прошли пути и до половины пути осталось еще пройти 6 км. Сколько км пути осталось пройти туристам?
Слайд 6
Задачи на модели «часть-целое» Задача 2. В классе число мальчиков составляет 80 % от числа девочек. Сколько процентов составляет число девочек от числа мальчиков в этом классе? Сколько процентов от числа всех учеников составляют мальчики?
Слайд 7
Задачи на модели «часть-целое» Задача 3. Студент купил 2 книги, уплатив за них 6 манат. Если бы первая книга стоила на 25% меньше, а вторая- на 50% больше, то цены книг были бы одинаковы. Сколько денег уплатил студент за каждую книгу?
Слайд 8: Задачи на модели «часть-целое»
Задача 4. Отец часть своей зарплаты отдал сыну, часть оставшихся денег дочери, затем 60% от еще оставшихся денег на коммунальные расходы. После чего в кармане отца осталось 216 манат. Какова зарплата отца?
Слайд 9: Задачи на модели «часть-целое»
Задача 5. Каждый из 2-х учеников купил одинаковые ручки. При этом первый заплатил часть имеющихся у него денег, а второй- часть своих денег. 1) Найдите отношение первоначальных сумм, имеющихся у них денег. 2) Найдите отношение оставшихся у них сумм денег.
Слайд 11: Отношение
Задача 7. Катер проплывает расстояние от порта А до порта В за 8 часов, а на обратный путь затрачивает 9 часов. а) Найдите отношение скорости течения реки к скорости катера. b) За какое время преодолеет это же расстояние плот?
Слайд 13: Пропорция
Пример 8. Упростите выражение , если Пример 9. Найдите произведение, если
Слайд 14: Пропорция
Пример 10. Найдите, если и Пример 11. Найдите значение выражения , если
Слайд 15: Величины
Прямо пропорциональные величины Обратно Пропорциональные величины постоянно
Слайд 16
Задача 12. Число 520 поделили на части прямо пропорционально числам 2 и 3 и обратно пропорционально числу 5. Найдите наименьшую часть.
Слайд 17
Задача 13. Как изменится объём цилиндра, если его высоту и диаметр основания увеличить в 3 раза? h d
Слайд 18
Задача 14. Для борьбы с пожаром были использованы 4 самолёта, которые оказались в состоянии сбросить в общей сложности 1200 воды за 2 часа колько самолётов Потребовалось для того, чтобы сбросить 1500 воды за 1 час?
Слайд 19
Задача 1 5. 3 маляра за 5 дней могут покрасить 60 окон. Сколько окон покрасят 5 маляров за 4 дня?
Слайд 20
Пример 1 6. Сколько процентов составляет НОД( a;b ) от НОК( a;b )? Задачи на проценты
Слайд 21
Задача 1 7. Сначала цена на товар понизилась на 30 %, а через год новая цена повысилась на 30 %. Как изменилась цена по сравнению с первоначальной?
Слайд 22
Задача 1 8. Цена товара увеличилась на 25%. На сколько процентов ее необходимо уменьшить, чтобы получить первоначальную цену?
Слайд 23
Задача 1 9. Цена на некоторый товар сначала повысилась на 20 %, затем ещё на 20 %. На сколько процентов она повысилась всего, если товар этот стоил 500 манат ?
Слайд 24
Задача 20. Цену на товар снизили сначала на 20%, а затем еще на 15%. При этом он стал стоить 2380 манат. Какова была первоначальная цена товара?
Слайд 25
Задача 21. Сначала число увеличили на 8%, затем его уменьшили в 6 раз. Как изменилось число?
Слайд 26
Задача 22. Груши, содержащие 70 % воды, потеряли при сушке 60 % своей массы. Сколько процентов воды содержат сушеные груши?
Слайд 27
Задача 2 3. Длину участка увеличили на 10 %, а ширину уменьшили на какое-то число процентов. В результате площадь участка уменьшилась на 1%. На сколько процентов уменьшили ширину участка?
Слайд 28: Простой и сложный процентный рост
-начальная сумма - конечная сумма -годовой процентный рост - срок хранения( в годах)
Слайд 29
Задача 24. Товар стоил 8 манат. После 3-х разового подорожания на одно и то же число процентов, цена товара стала 27 манат. На сколько процентов каждый раз увеличивалась стоимость товара?
Слайд 30
Задача 2 5. Банк выплачивает вкладчикам каждый месяц 2% от внесённой суммы. Клиент сделал вклад в размере 500 манат. Какая сумма будет на его счёте через полгода?
Слайд 31
Задачи на раствор К 400г 20% раствора соли добавили а) 100г воды b) 100 г соли c) 100г 60% раствора этой же соли Найдите процентное содержание соли в полученном растворе.
Слайд 32
Задача 2 6. Сколько граммов воды надо выпарить из 200г 15%- го сахарного раствора, чтобы получить 20% раствор?
Слайд 33
Задача 27. Товар с 14% убытком продан за 344 манат. Сколько будет стоить этот товар с 20 % прибылью?
Слайд 34: Дополнительные задания
Задача 2 8. Имеются два сплава золота и серебра. В одном сплаве количество этих металлов находится в отношении 2:3, а в другом – в отношении 3:7. Сколько нужно взять каждого сплава, чтобы получить 8кг нового сплава, в котором золото и серебро были бы в отношении 5:11? Дополнительные задания
Слайд 35
Задача 2 9. Из сосуда ёмкостью 54 литра, наполненного кислотой, вылили несколько литров и долили сосуд водой. Потом опять вылили столько же литров смеси. Тогда в оставшейся в сосуде смеси оказалось 24 литра чистой кислоты. Сколько кислоты вылили в первый раз?
Слайд 36
Задача 30. Смешав 8% и 13% растворы соли и добавив 200 миллилитров 5% раствора соли, получили 7% раствор соли. Если бы вместо 200 миллилитров 5% раствора соли добавили 300 миллилитров 17% раствора соли, то получили бы 15% раствор соли. Сколько миллилитров 8% и 13% растворов соли использовали для получения раствора?