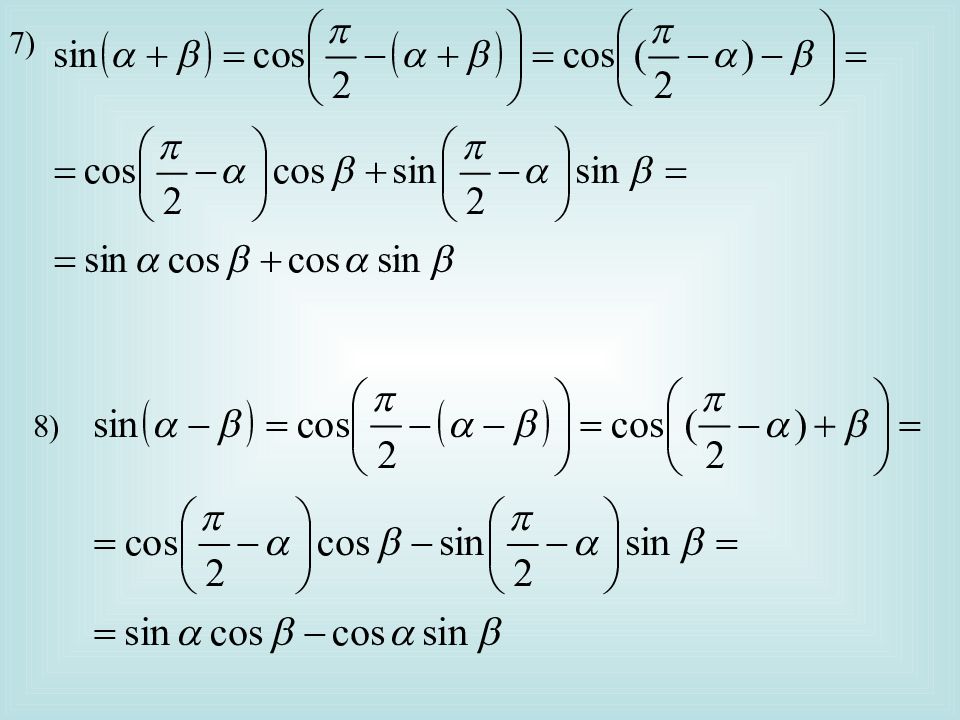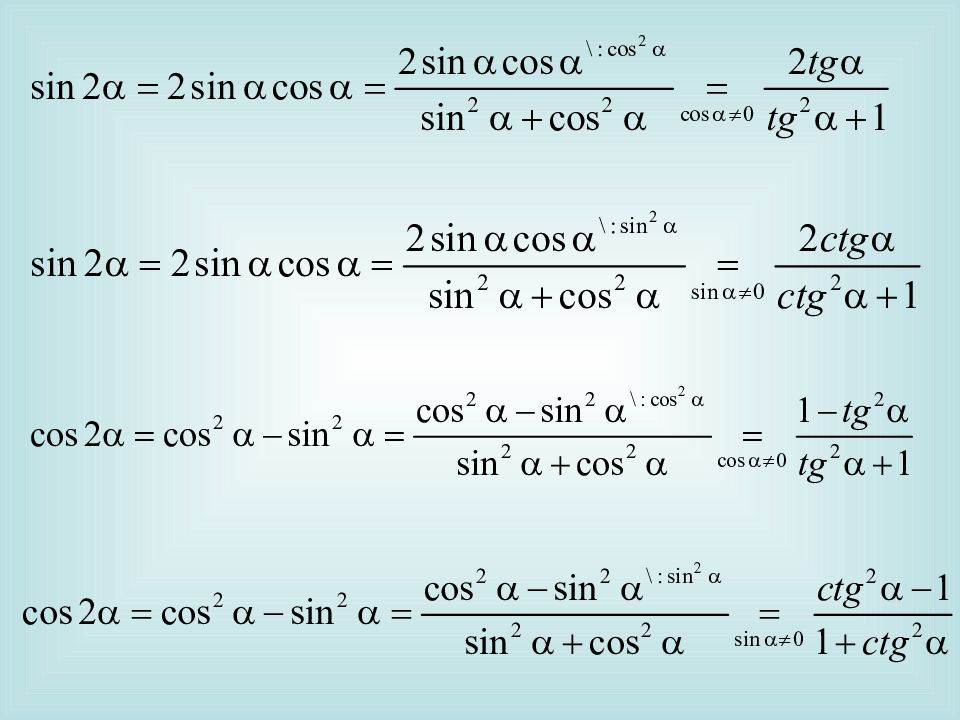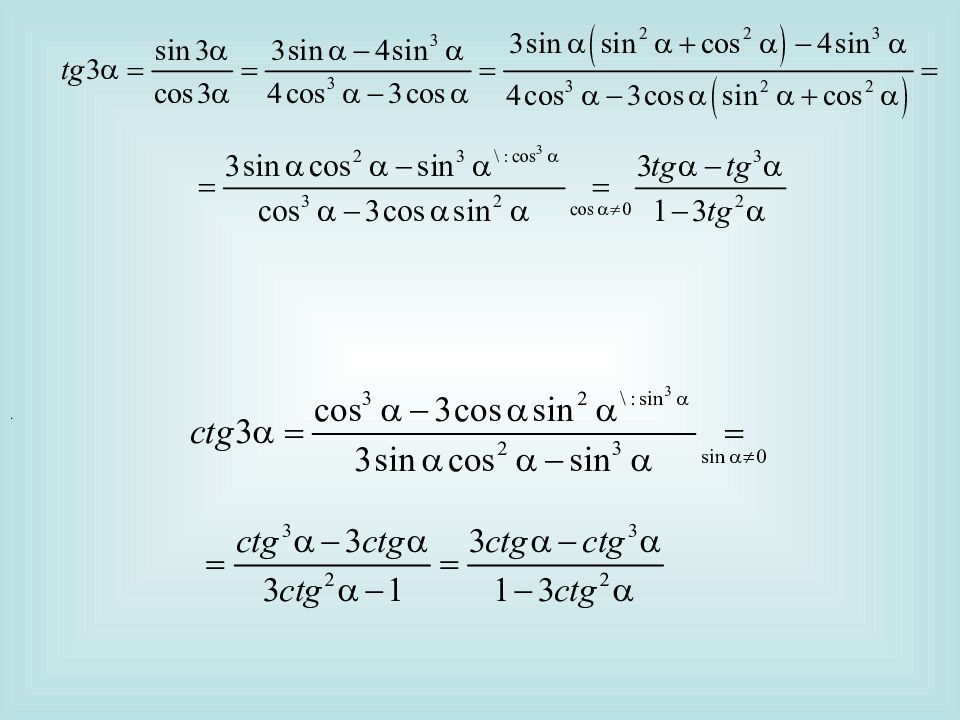Преобразование тригонометрических выражений (вывод тригонометрических формул)
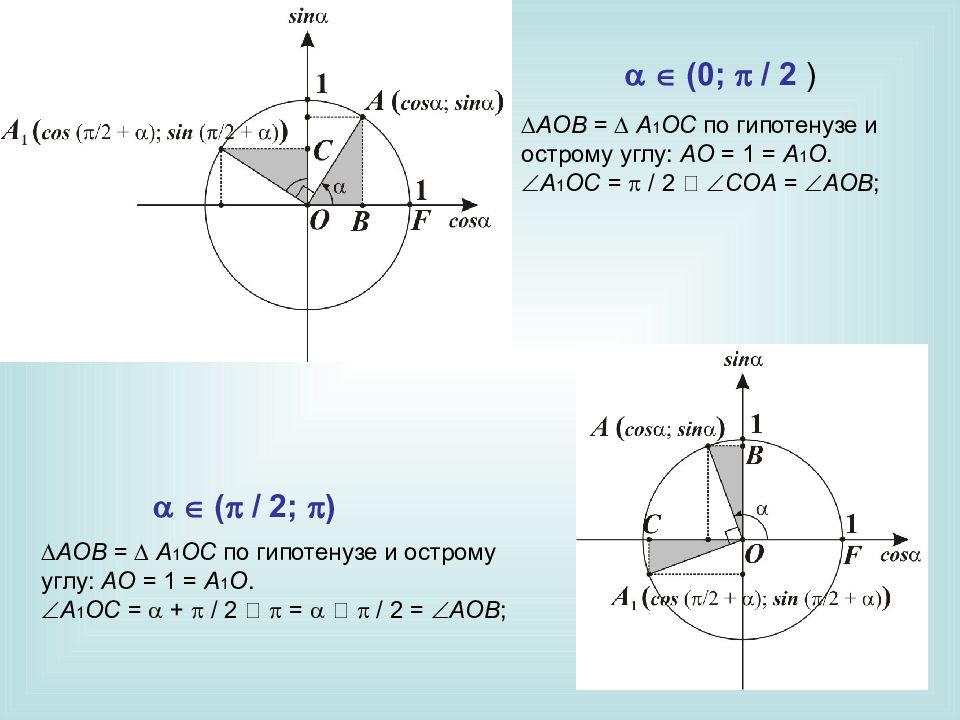
I-a. Формулы приведения Выведем вспомогательные формулы, позволяющие находить и по тригонометрическим функциям угла .
AOB = A 1 OC по гипотенузе и острому углу: AO = 1 = A 1 O. A 1 OC = / 2 ‑ COA = AOB ; AOB = A 1 OC по гипотенузе и острому углу: AO = 1 = A 1 O. A 1 OC = + / 2 ‑ = ‑ / 2 = AOB ; (0; / 2 ) ( / 2; )
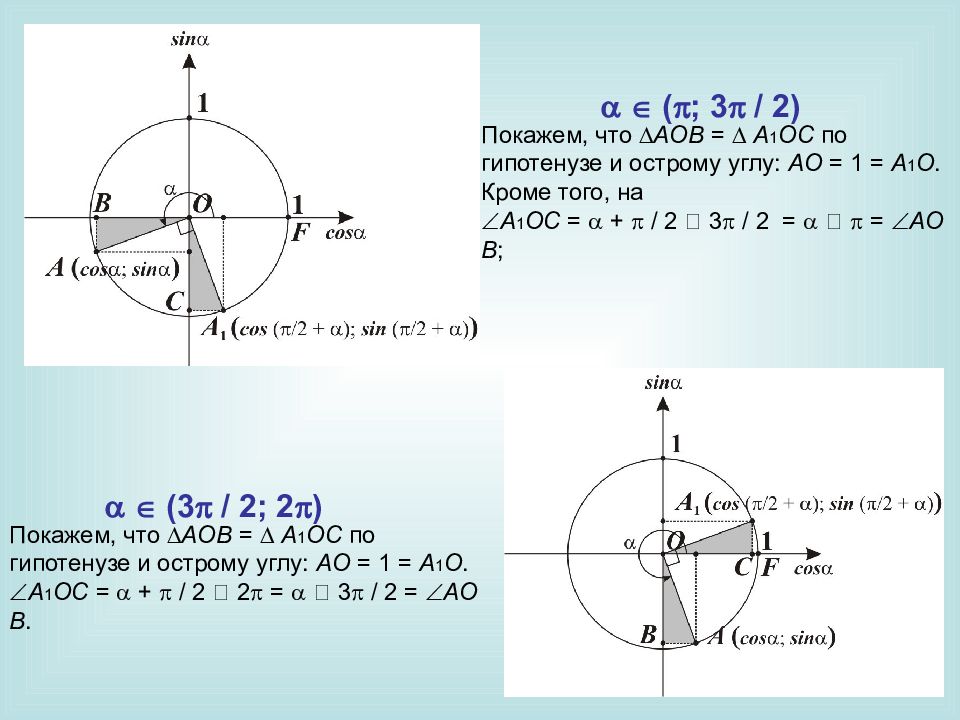
Покажем, что AOB = A 1 OC по гипотенузе и острому углу: AO = 1 = A 1 O. Кроме того, на A 1 OC = + / 2 ‑ 3 / 2 = ‑ = AOB ; Покажем, что AOB = A 1 OC по гипотенузе и острому углу: AO = 1 = A 1 O. A 1 OC = + / 2 ‑ 2 = ‑ 3 / 2 = AOB. ( ; 3 / 2) (3 / 2; 2 )
, . I-a. Формулы приведения
II. Формулы сложения 0 1) Отметим на единичной окружности точки и 2) Введем единичные вектора и 4 ) 3) 4) Угол между векторами и равен
5) По свойству скалярного произведения найдем 6) Учитывая четность тригонометрических функций получаем
7) 8)
II. Формулы сложения
определены: и , т.е. в случае, когда и Поделим числитель и знаменатель полученной дроби на
II. Формулы сложения
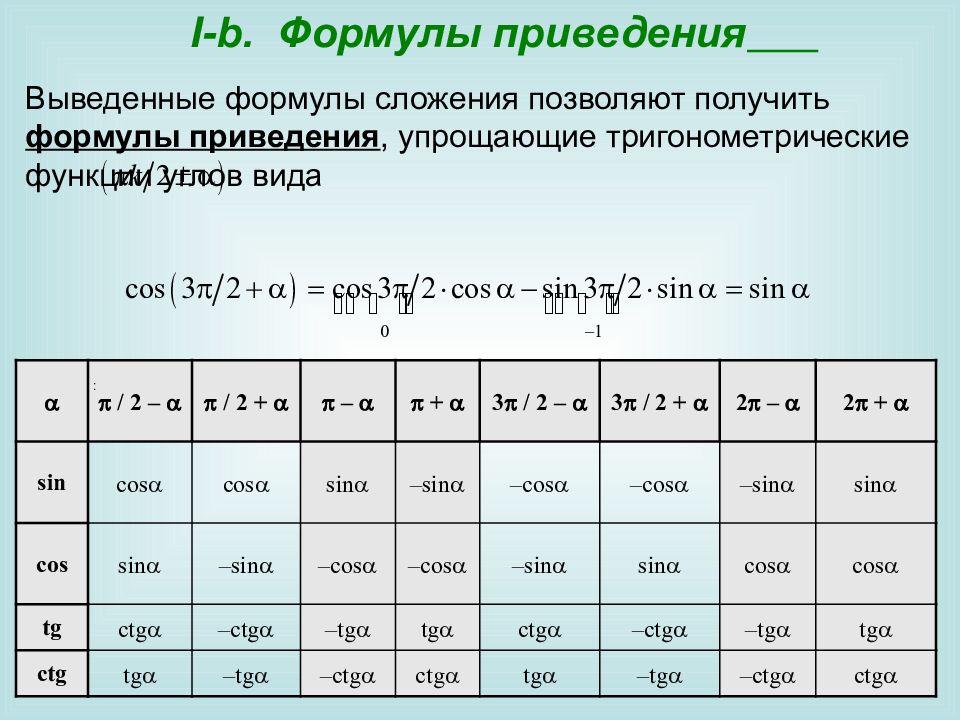
/ 2 – / 2 + – + 3 / 2 – 3 / 2 + 2 – 2 + sin cos cos sin – sin – cos – cos – sin sin cos sin – sin – cos – cos – sin sin cos cos tg ctg – ctg – tg tg ctg – ctg – tg tg ctg tg – tg – ctg ctg tg – tg – ctg ctg I-b. Формулы приведения Выведенные формулы сложения позволяют получить формулы приведения, упрощающие тригонометрические функции углов вида :
III. Формулы двойных углов Чтобы вывести формулы для вычисления тригонометрических функций двойного аргумента, подставим = в формулы сложения:
III. Формулы двойных углов
III. Формулы двойных углов
III. Формулы двойных углов
. IV. Формулы тройных углов
.
IV. Формулы тройных углов
V. Формулы половинных углов . .
;
V. Формулы половинных углов , . , .
VI. Формулы преобразования произведения тригонометрических функций в сумму . Сложив почленно равенства (3) и (4), получим: . Вычтя из равенства (4) равенство (3), получим: . Сложив почленно равенства (1) и (2), получим:
VI. Формулы преобразования произведения тригонометрических функций в сумму
VII. Формулы преобразования суммы тригонометрических функций в произведение .
. .
VII. Формулы преобразования суммы тригонометрических функций в произведение
