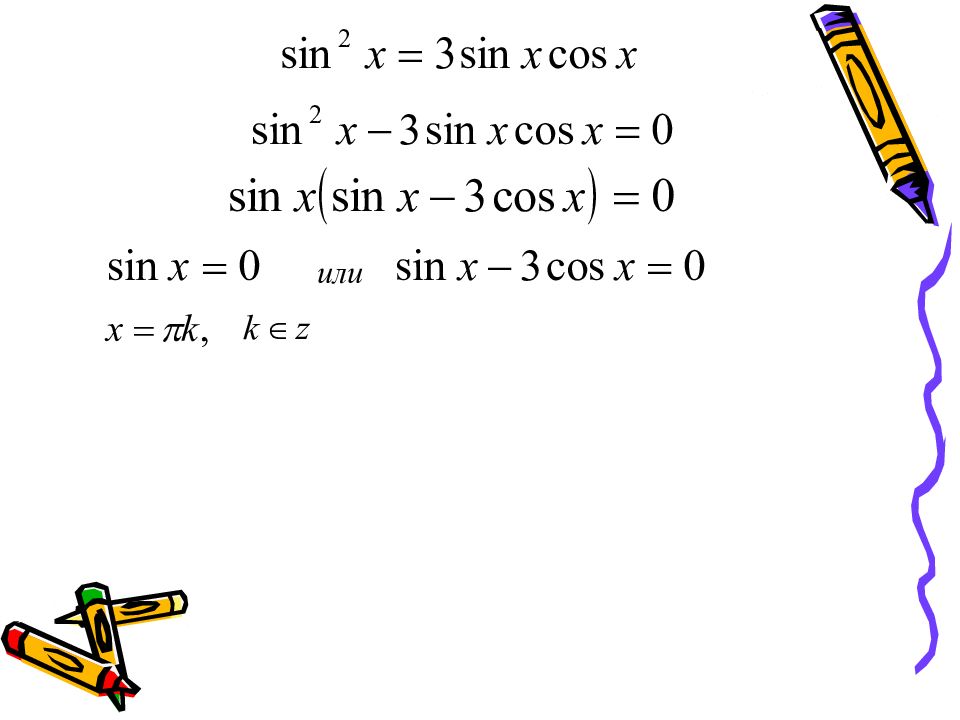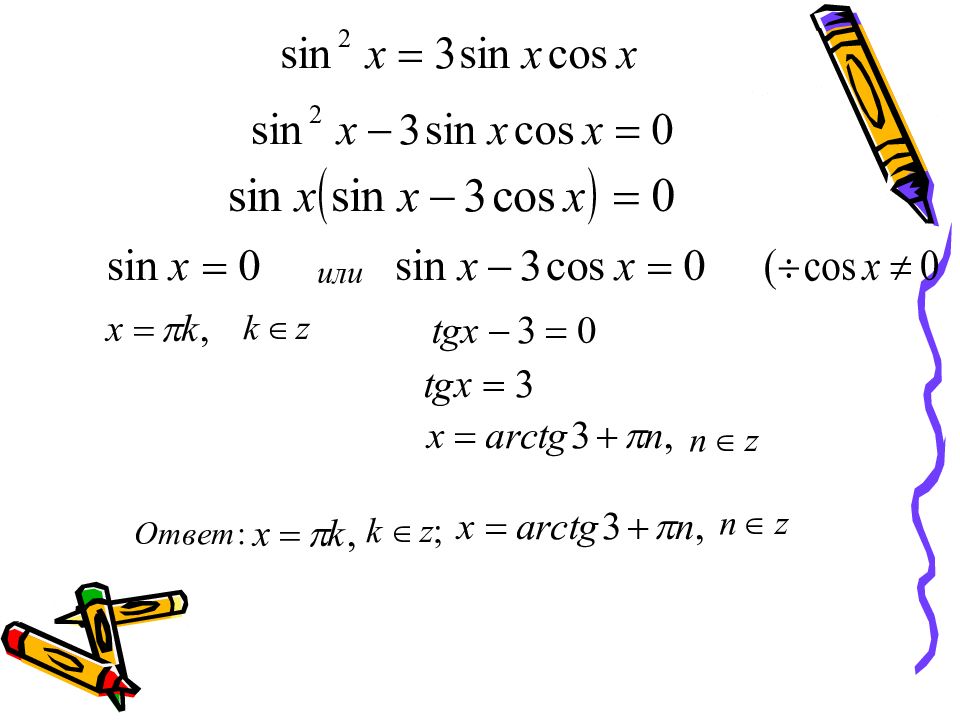Алгебра 10 класс Тема: «Способы решения тригонометрических уравнений»
Знать: Свойства тригонометрических функций. Определения обратных тригонометрических функций. Формулы тригонометрии. Формулы решения простейших тригонометрических уравнений. Уметь: Вычислять значения тригонометрических функций. Вычислять значения обратных тригонометрических функций. Решать простейшие тригонометрические уравнения. Выполнять тождественные преобразования выражений.
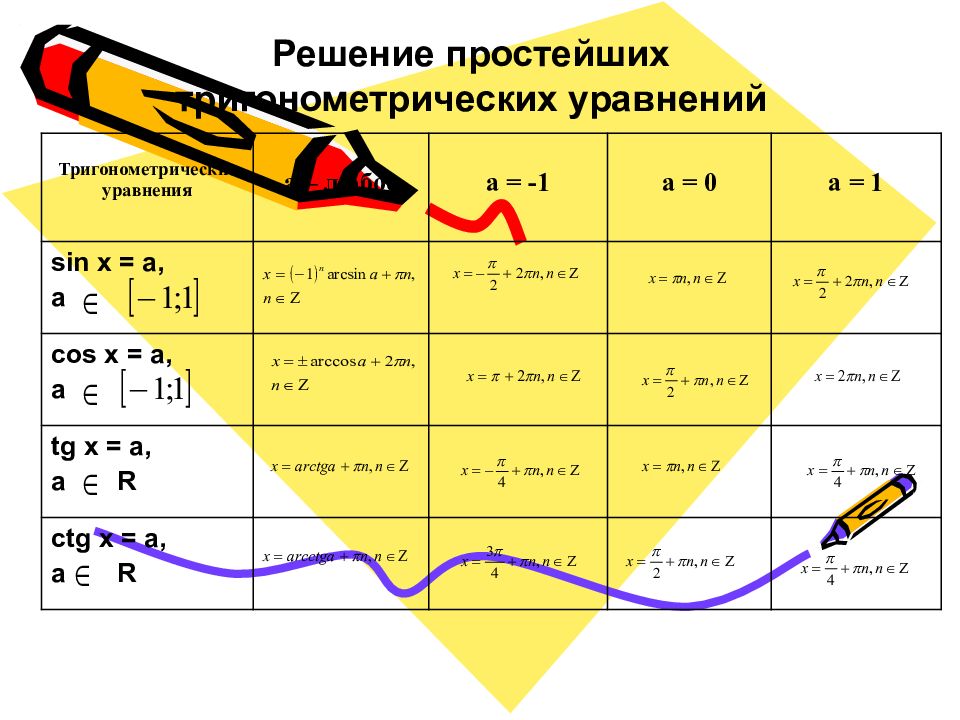
Тригонометрические уравнения а – любое а = -1 а = 0 а = 1 sin x = a, a cos x = a, a tg x = a, a R ctg x = a, a R Решение простейших тригонометрических уравнений
Разложение на множители Сведение к алгебраическому уравнению Введение вспомогательного угла Универсальная подстановка Сведение к однородному уравнению Использование формул преобразования суммы в произведение и обратно Применение формул понижения степени Обращение к условию равенства одноименных тригонометрических функций Использование свойства ограниченности функций (метод оценки)
Знать: Способы решения тригонометрических уравнений: сведения к квадратному уравнению разложения на множители понижения степени. однородные уравнения введения вспомогательного угла. Уметь: Классифицировать тригонометрические уравнения по способу решения. Решать тригонометрические уравнения следующими способами: способом сведения к квадратному уравнению способом разложения на множители способом понижения степени. однородные уравнения. способом введения вспомогательного угла.
«Метод решения хорош, если с самого начала мы можем предвидеть – и впоследствии подтвердить это, - что, следуя этому методу, мы достигнем цели.»
Пусть a = sin x Ответ:
Пусть a = sin x уравнение решения не имеет, так как Ответ:
Пусть a = ctg x Выполним обратную замену Ответ:
Привести уравнение к квадратному, относительно тригонометрических функций, применяя тригонометрические тождества. Ввести новую переменную. Записать данное уравнение, используя эту переменную. Найти корни полученного квадратного уравнения. Перейти от новой переменной к первоначальной. Решить простейшие тригонометрические уравнения. Записать ответ.
Ответ:
Первой степени: a∙sinx + b∙cosx = 0 Т.к. sinx и cosx одновременно не равны нулю, то разделим обе части уравнения на cosx (или на sinx ). Получим: простое уравнение a∙tgx + b = 0 или tgx = m. Второй степени: a∙sin²x + b∙sinx∙cosx + c∙cos²x = 0 Разделим обе части на cos²x. Получим квадратное уравнение: a∙tg²x + b∙tgx + c = 0.
Пусть a = tg x Ответ: Однородные уравнения
Ответ: Метод понижения степени
Метод понижения степени Ответ:
>0
Правила. Увидел квадрат – понижай степень. Увидел произведение – делай сумму. Увидел сумму – делай произведение.
Проблемы, возникающие при решении тригонометрических уравнений.
1.Потеря корней: делим на g (х). опасные формулы (универсальная подстановка). Этими операциями мы сужаем область определения. 2. Лишние корни: возводим в четную степень. умножаем на g (х) (избавляемся от знаменателя). Этими операциями мы расширяем область определения.
«Мне приходится делить время между политикой и уравнениями. Однако уравнения, по-моему, гораздо важнее. Политика существует только для данного момента, а уравнения будут существовать вечно.» А. Эйнштейн
