Слайд 5
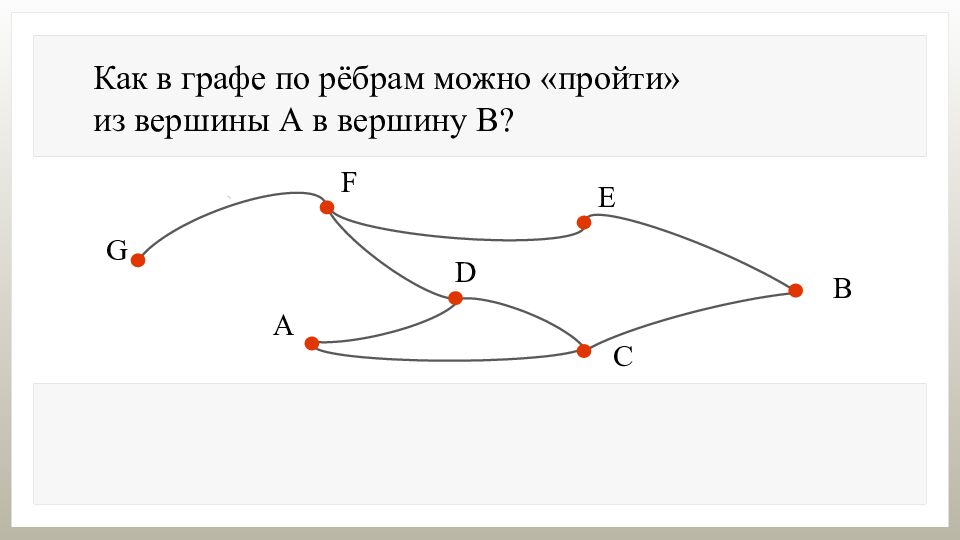
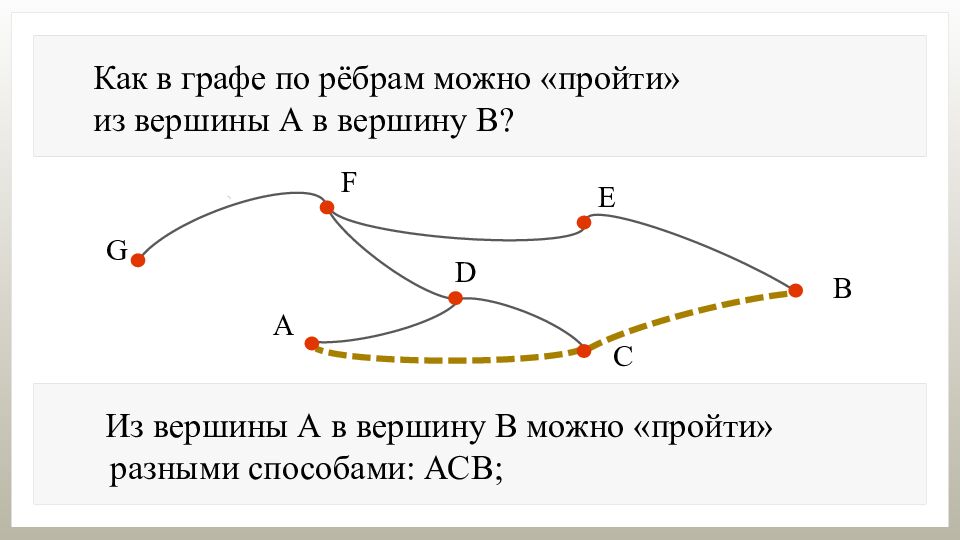
Как в графе по рёбрам можно «пройти» из вершины А в вершину В? Из вершины А в вершину В можно «пройти» разными способами: АСВ;
Слайд 6
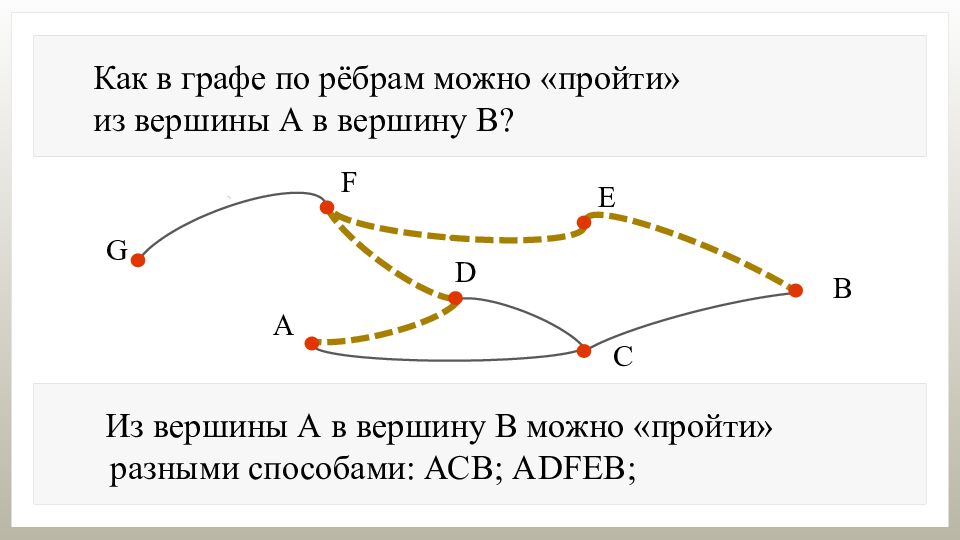
Как в графе по рёбрам можно «пройти» из вершины А в вершину В? Из вершины А в вершину В можно «пройти» разными способами: АСВ; А DFEB ;
Слайд 7
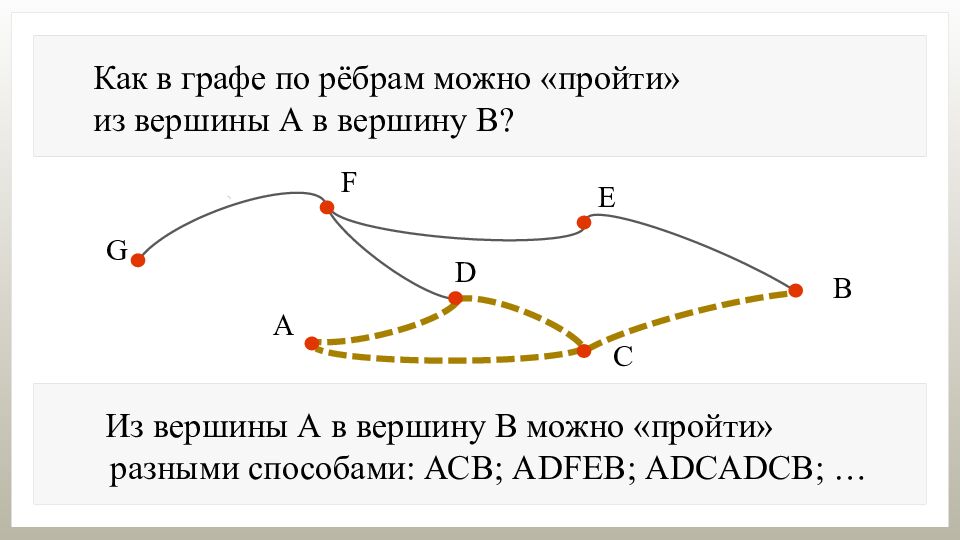
Как в графе по рёбрам можно «пройти» из вершины А в вершину В? Из вершины А в вершину В можно «пройти» разными способами: АСВ; А DFEB ; ADCADCB ; …
Слайд 8
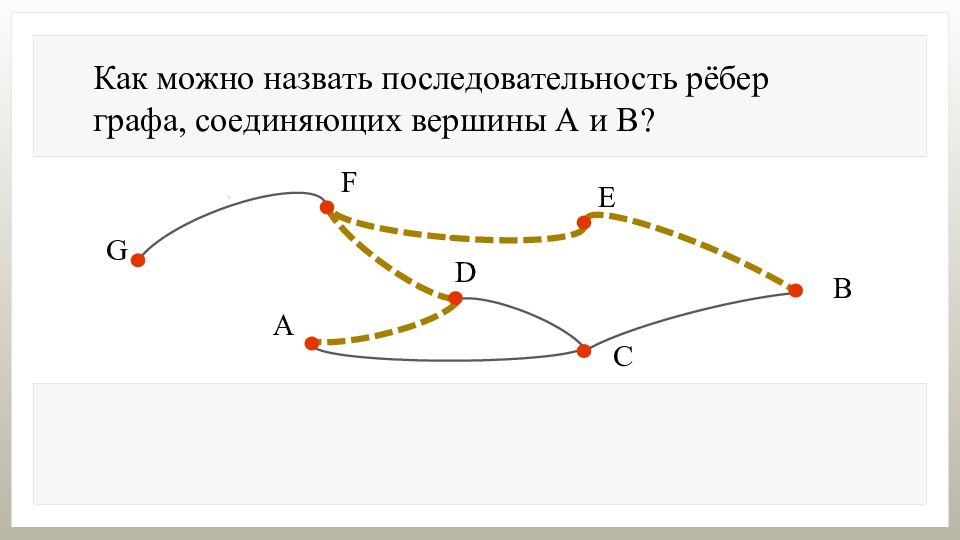
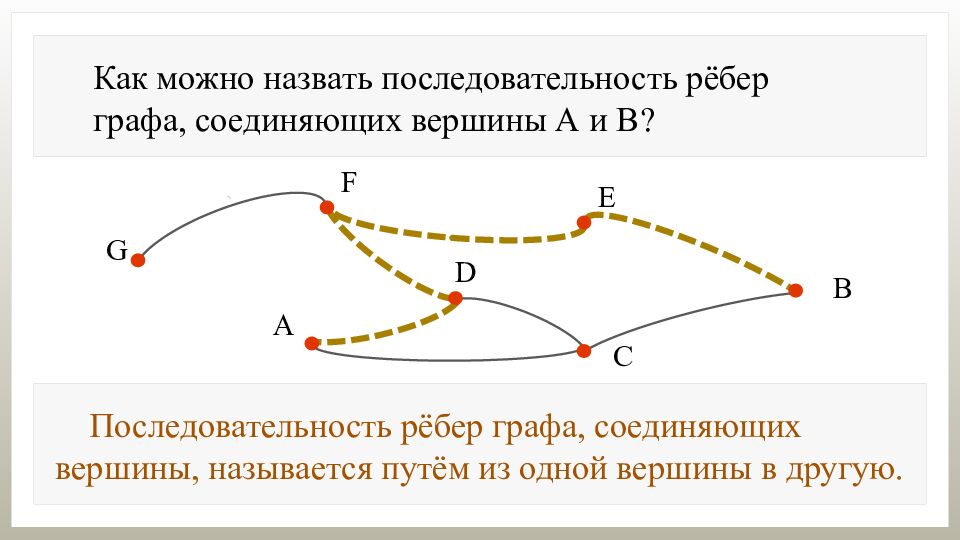
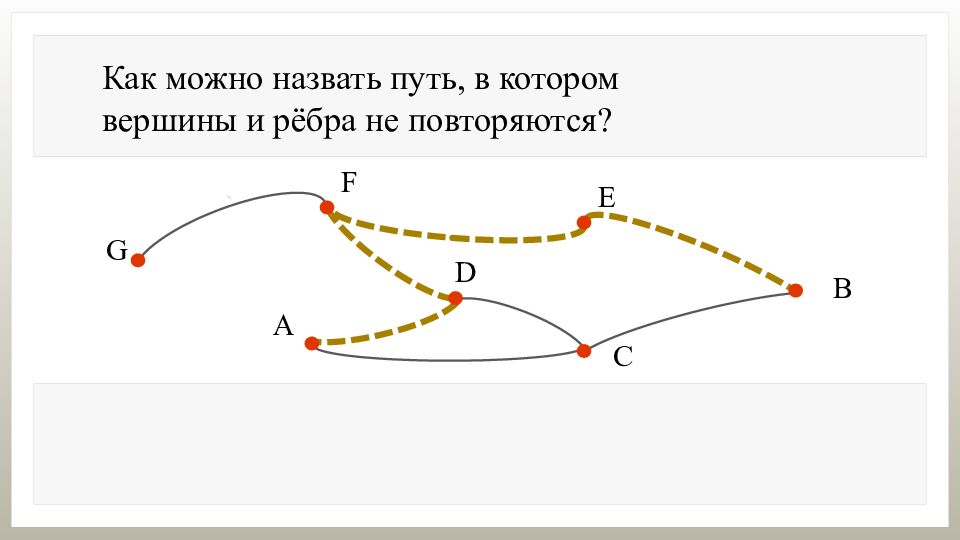
Как можно назвать последовательность рёбер графа, соединяющих вершины А и В?
Слайд 9
Как можно назвать последовательность рёбер графа, соединяющих вершины А и В? Последовательность рёбер графа, соединяющих вершины, называется путём из одной вершины в другую.
Слайд 11
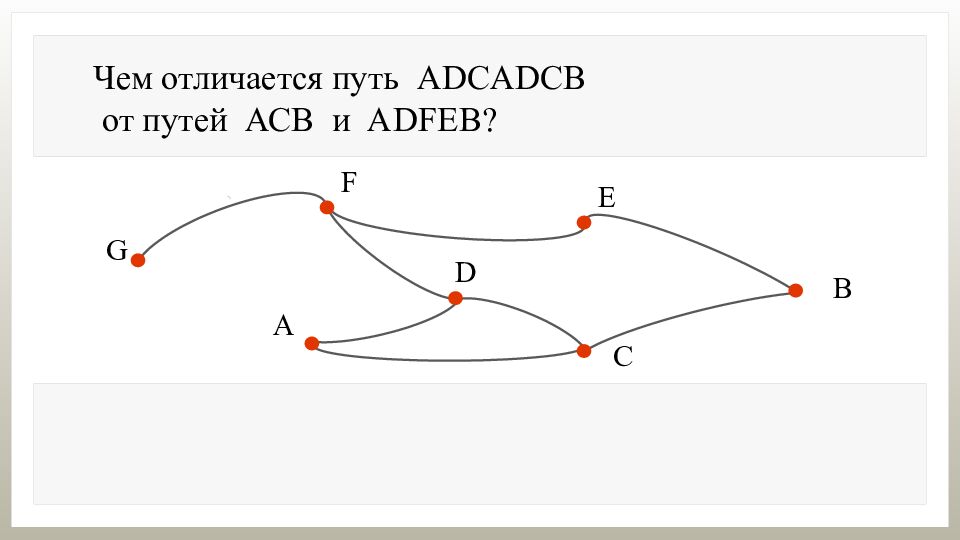
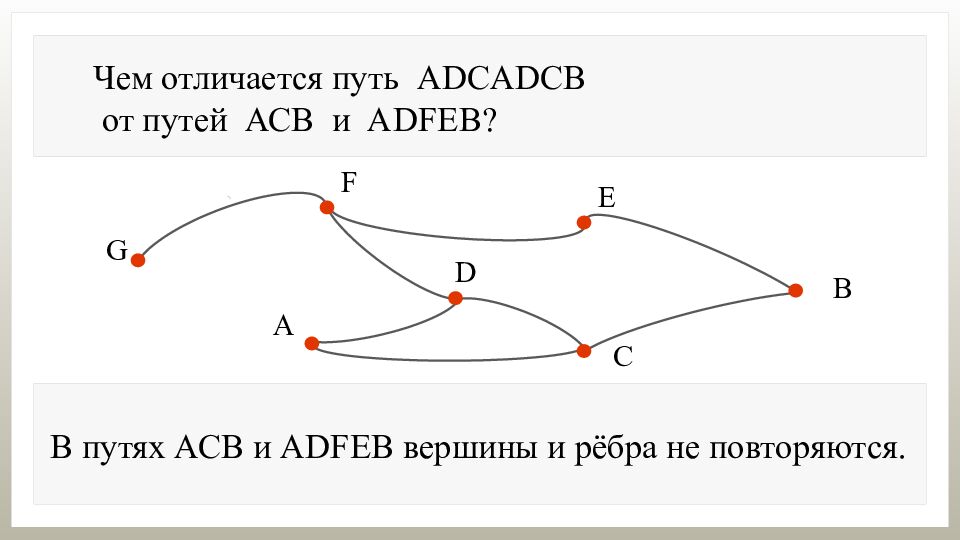
Чем отличается путь ADCADCB от путей АСВ и А DFEB ? В путях АСВ и А DFEB вершины и рёбра не повторяются.
Слайд 13
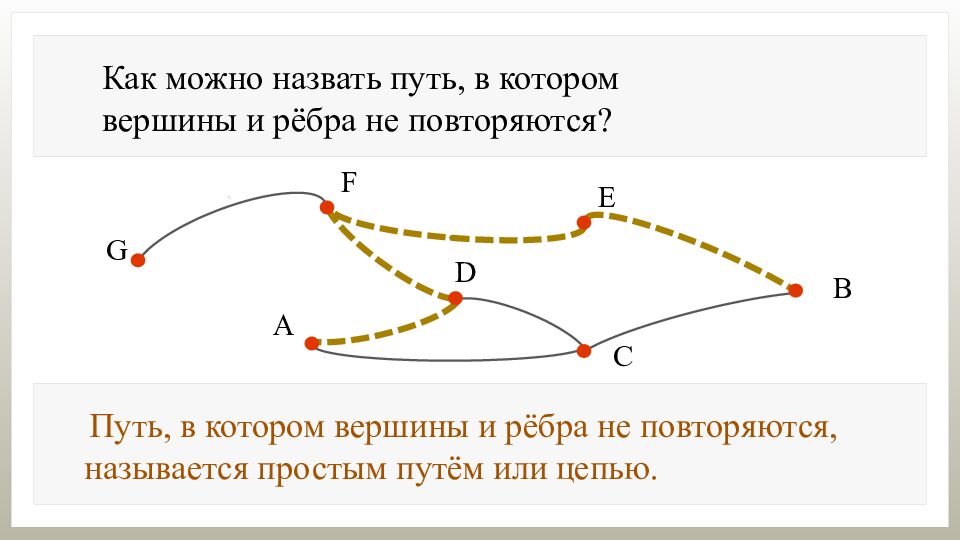
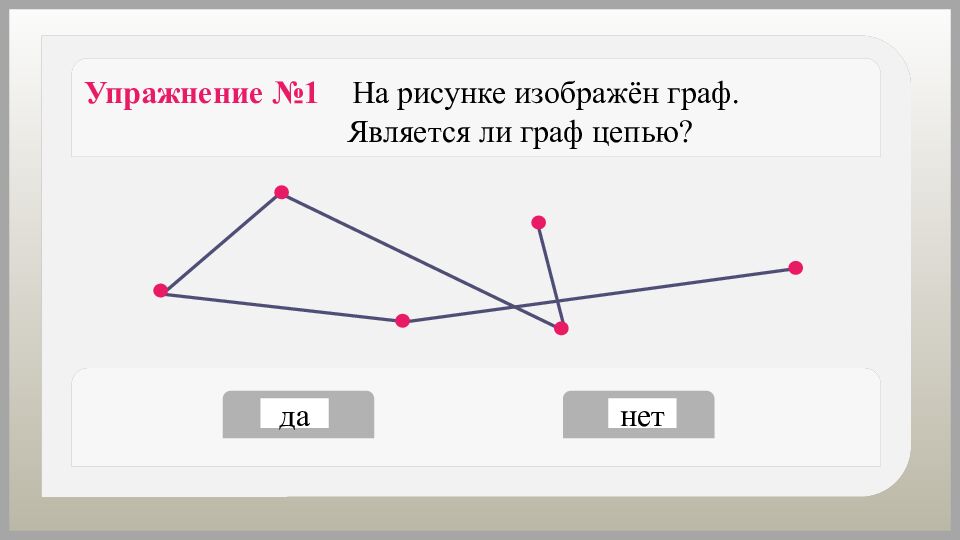
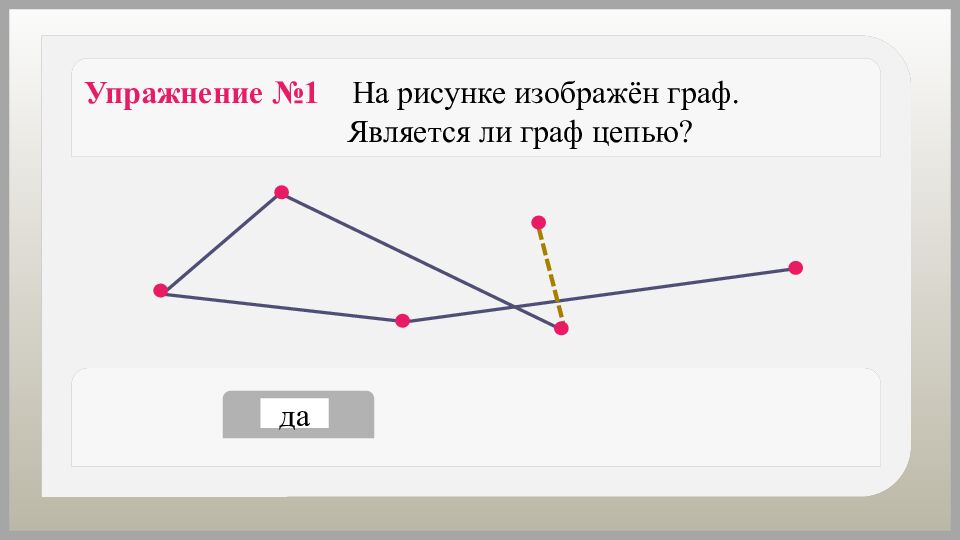
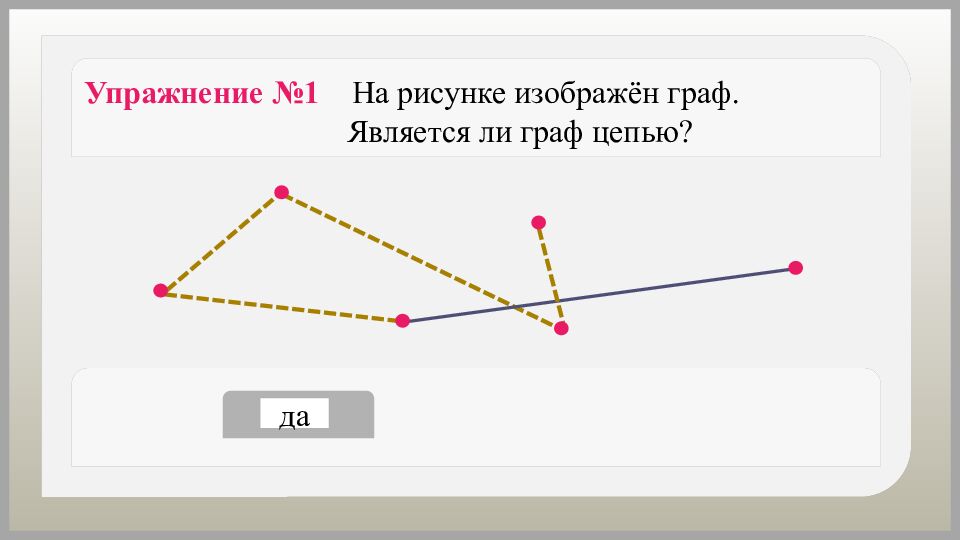
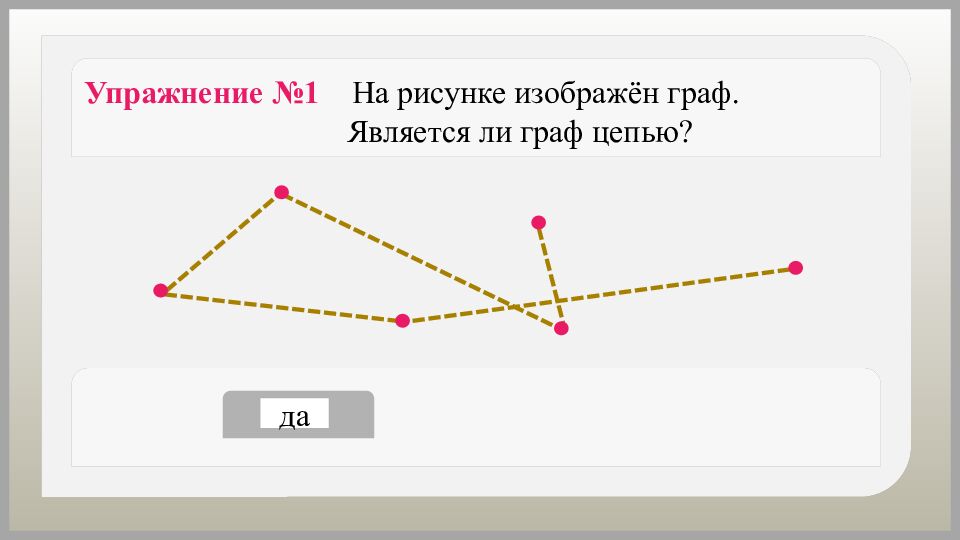
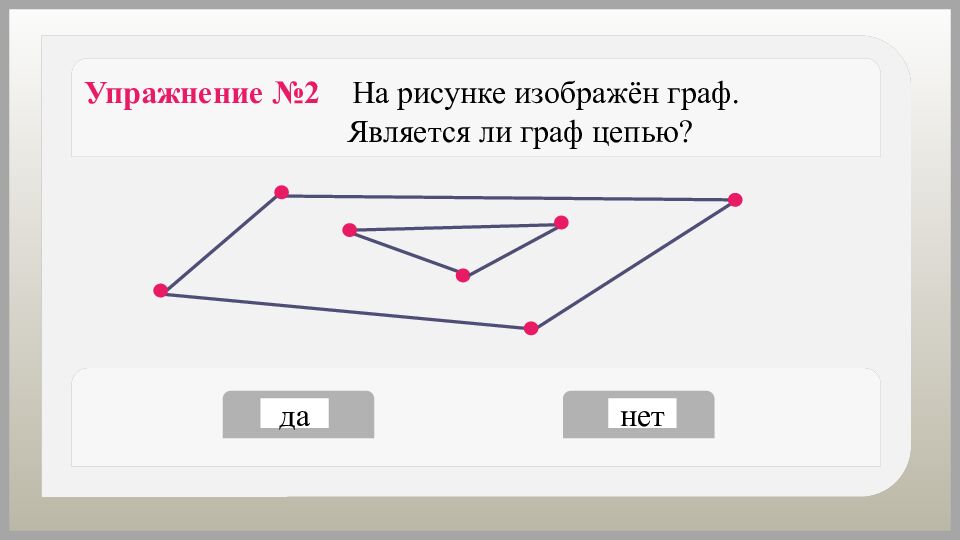
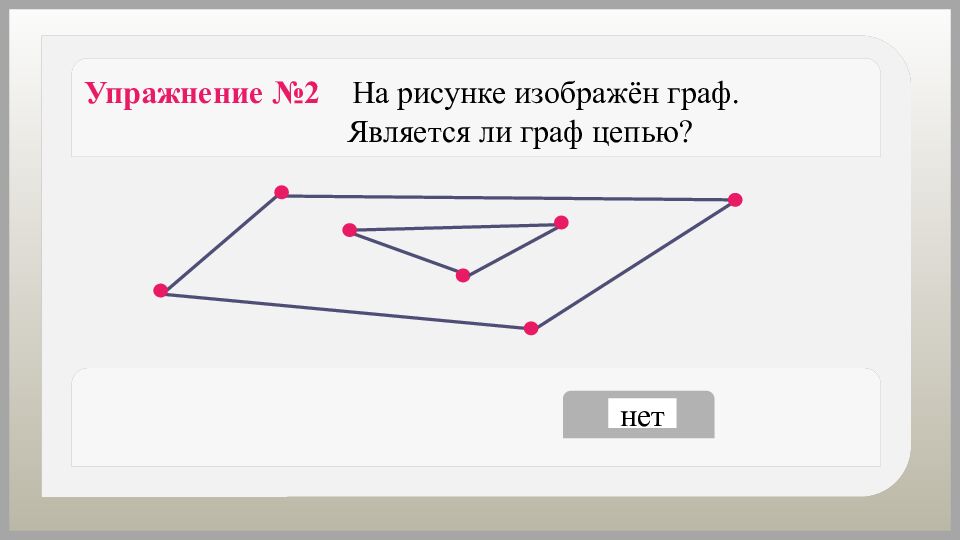
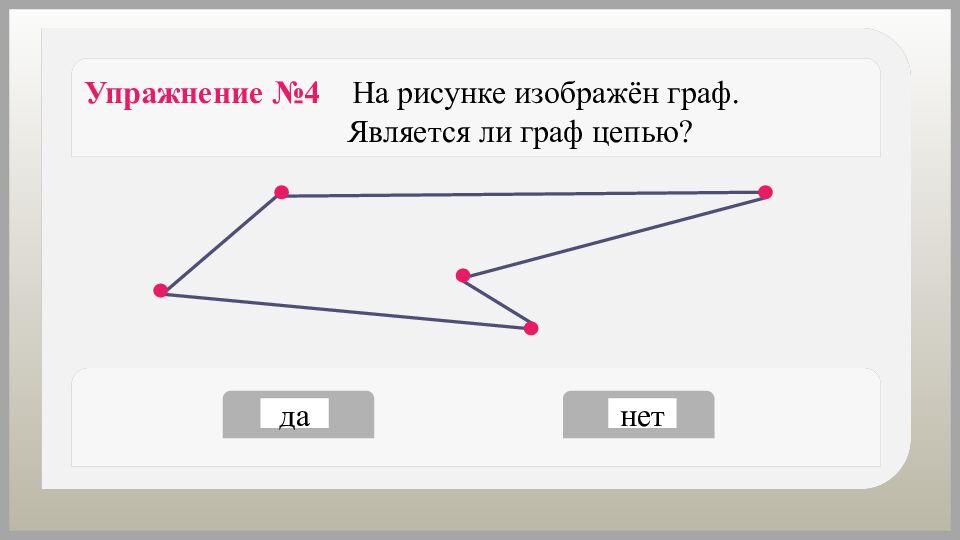
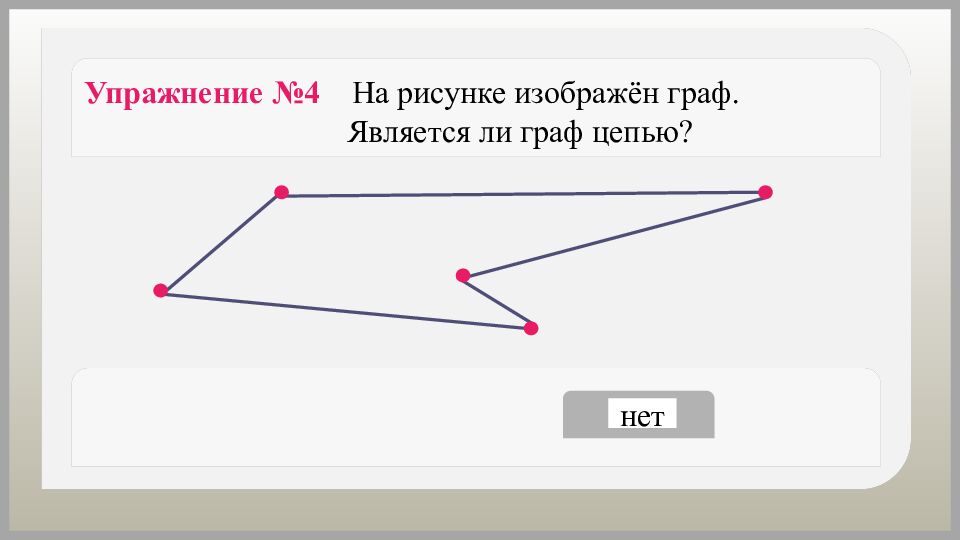
Как можно назвать путь, в котором вершины и рёбра не повторяются? Путь, в котором вершины и рёбра не повторяются, называется простым путём или цепью.
Слайд 14
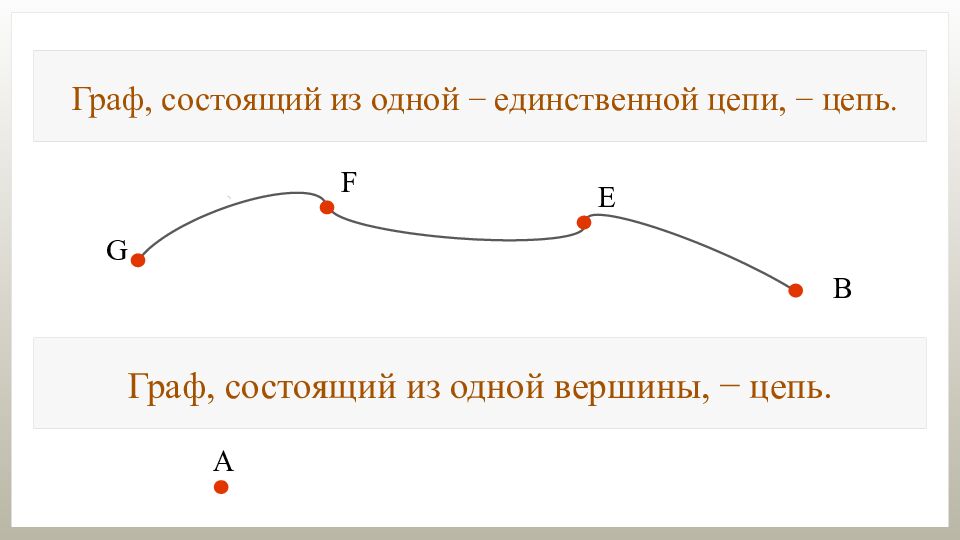
Граф, состоящий из одной − единственной цепи, − цепь. Граф, состоящий из одной вершины, − цепь.
Слайд 16
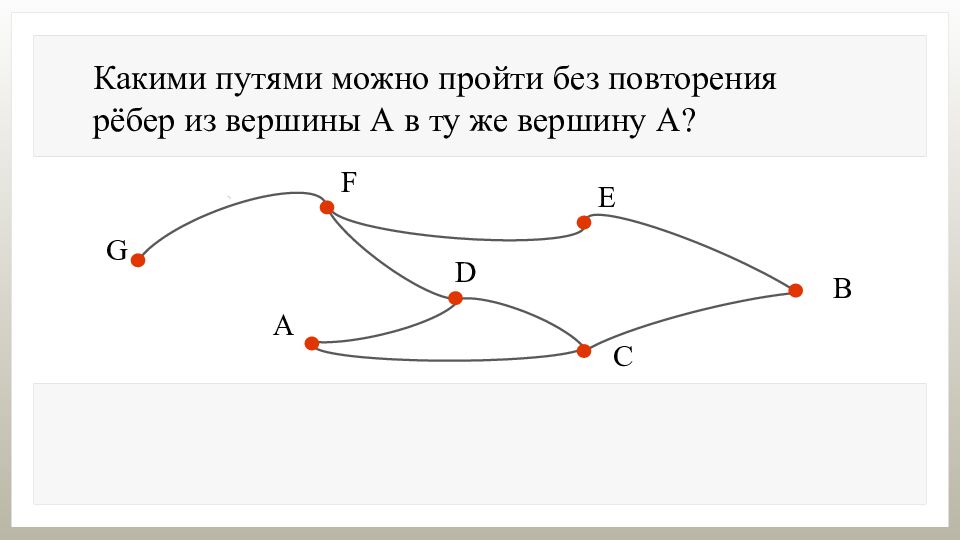
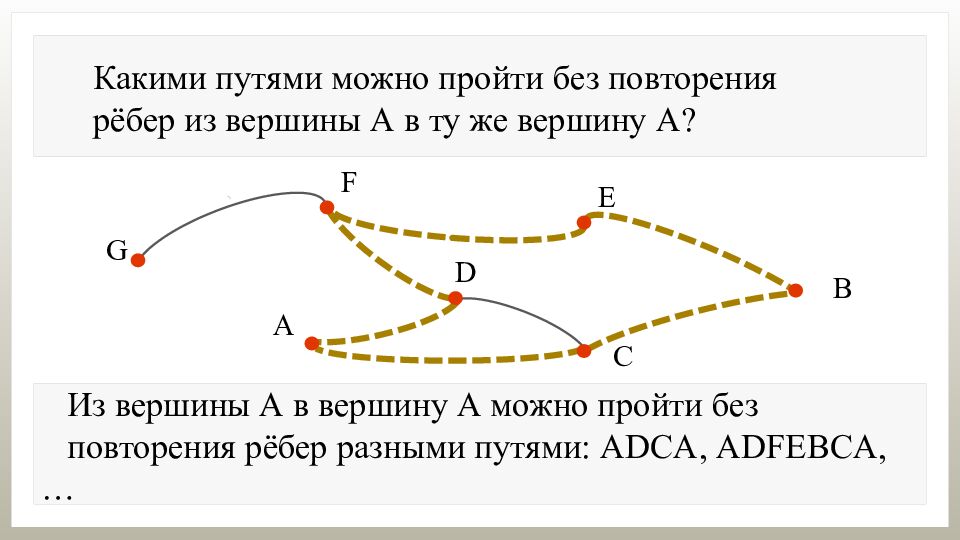
Какими путями можно пройти без повторения рёбер из вершины А в ту же вершину А?
Слайд 17
Какими путями можно пройти без повторения рёбер из вершины А в ту же вершину А? Из вершины А в вершину А можно пройти без повторения рёбер разными путями: ADCA,
Слайд 18
Какими путями можно пройти без повторения рёбер из вершины А в ту же вершину А? Из вершины А в вершину А можно пройти без повторения рёбер разными путями: ADCA, ADFEBCA,…
Слайд 19
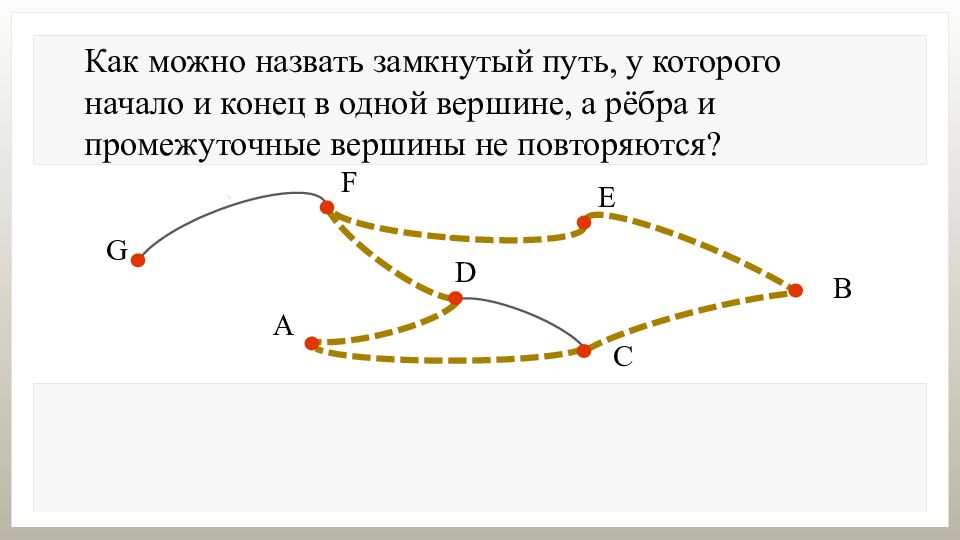
Как можно назвать замкнутый путь, у которого начало и конец в одной вершине, а рёбра и промежуточные вершины не повторяются?
Слайд 20
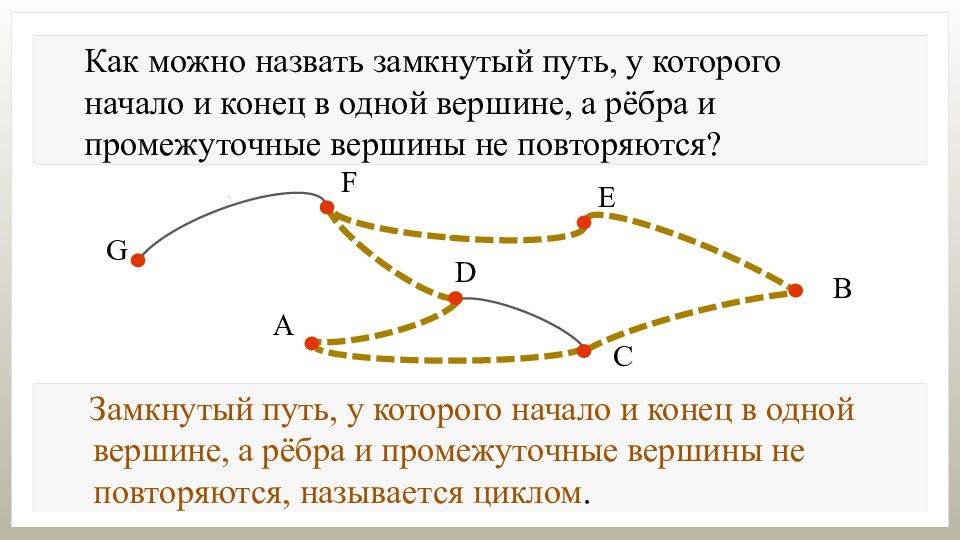
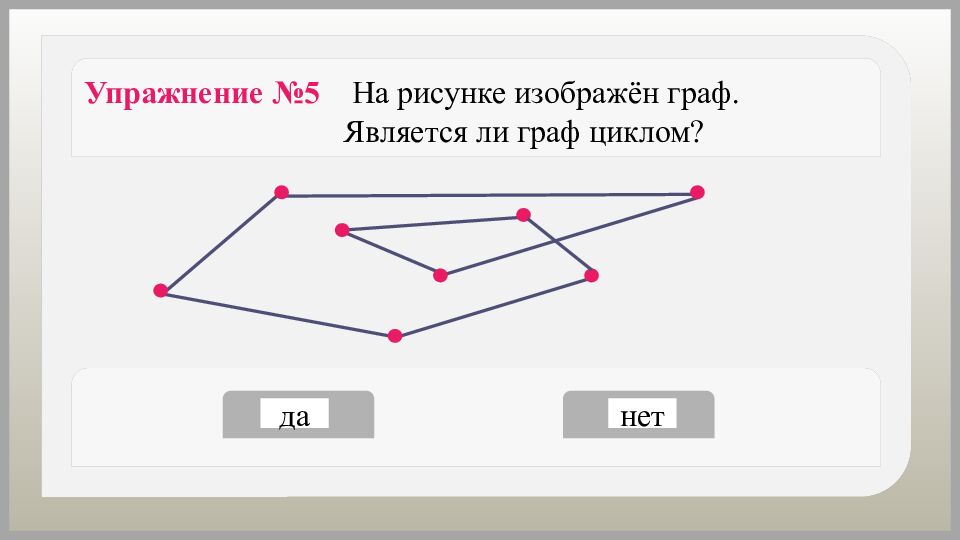
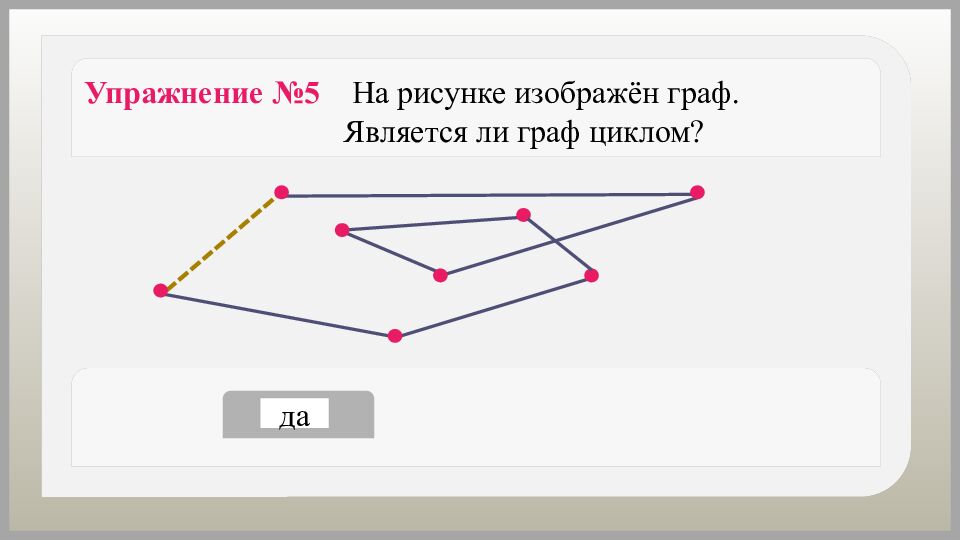
Как можно назвать замкнутый путь, у которого начало и конец в одной вершине, а рёбра и промежуточные вершины не повторяются? Замкнутый путь, у которого начало и конец в одной вершине, а рёбра и промежуточные вершины не повторяются, называется циклом.
Слайд 21
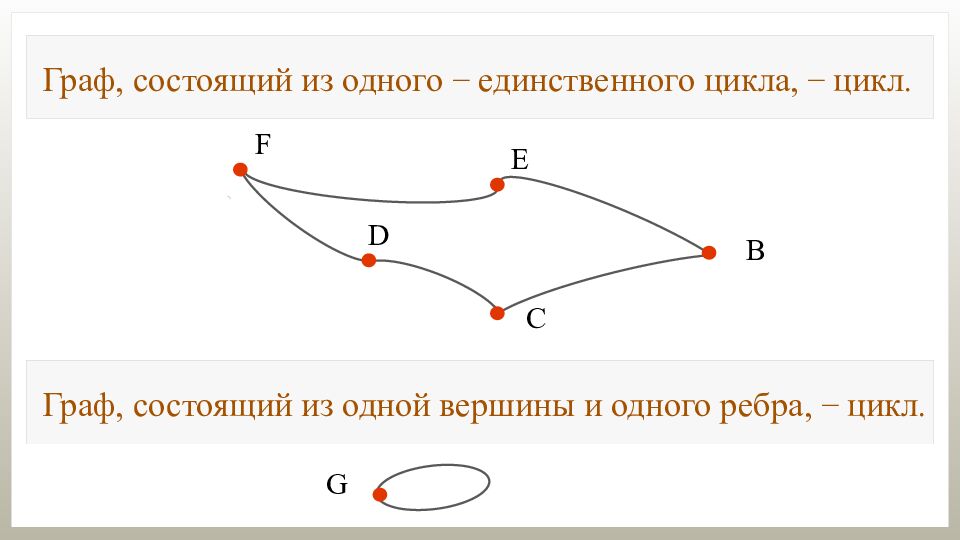
Граф, состоящий из одного − единственного цикла, − цикл. Граф, состоящий из одной вершины и одного ребра, − цикл.
Слайд 24
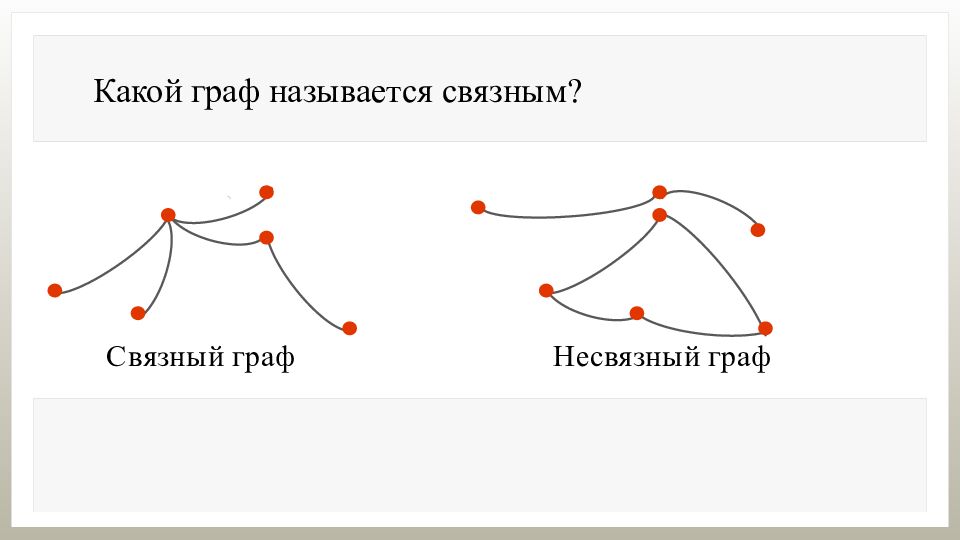
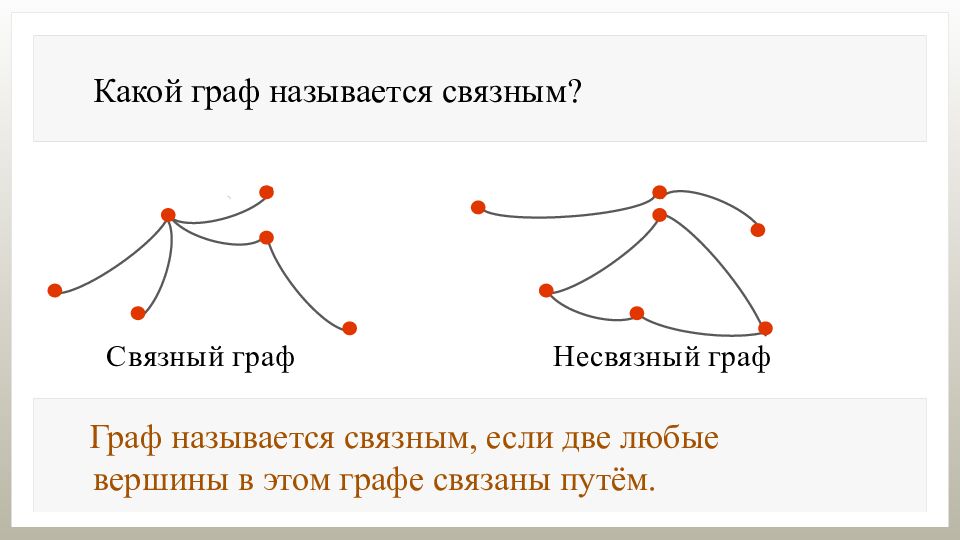
Какой граф называется связным? Граф называется связным, если две любые вершины в этом графе связаны путём.
Слайд 38
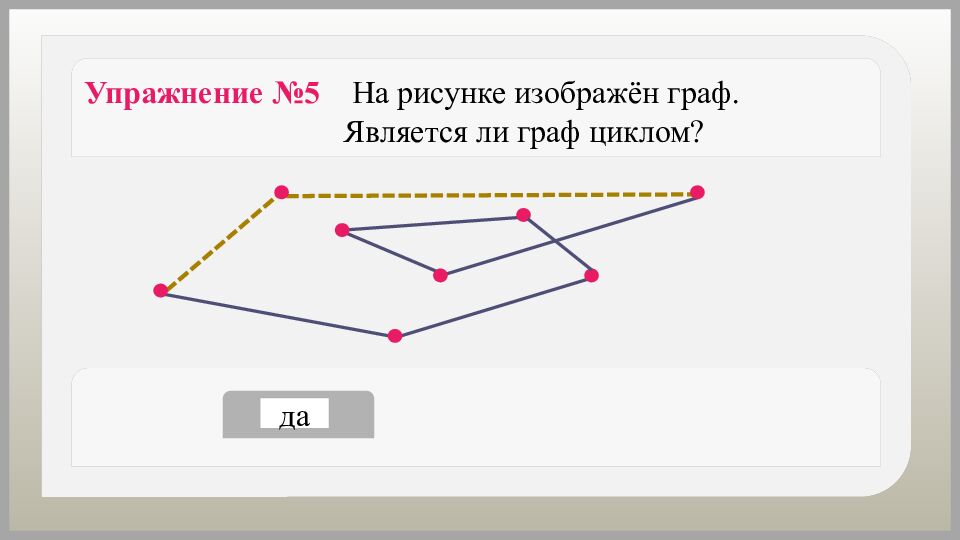
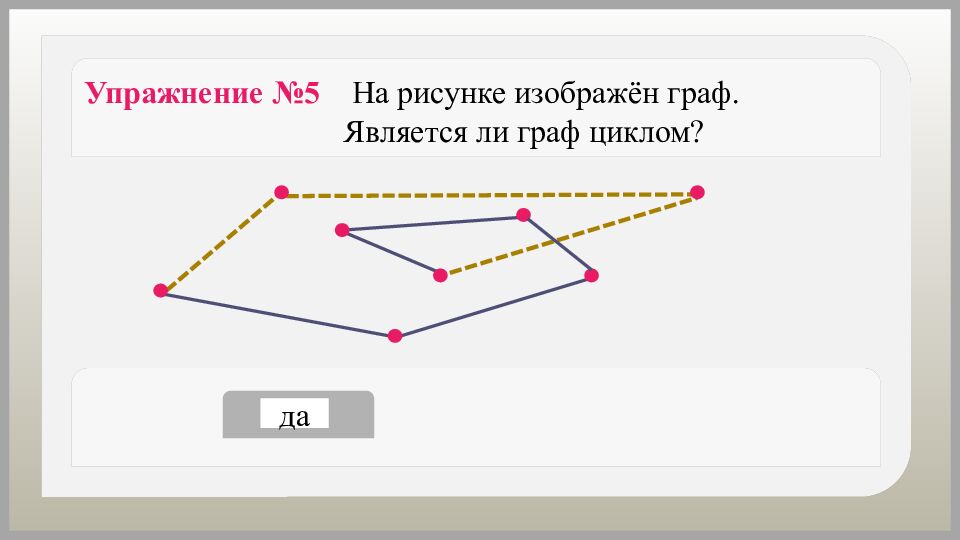
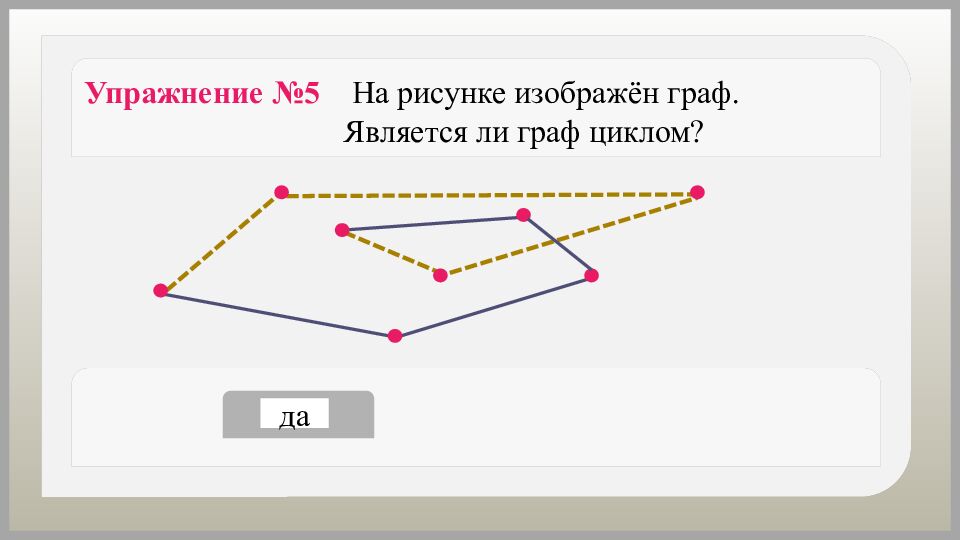
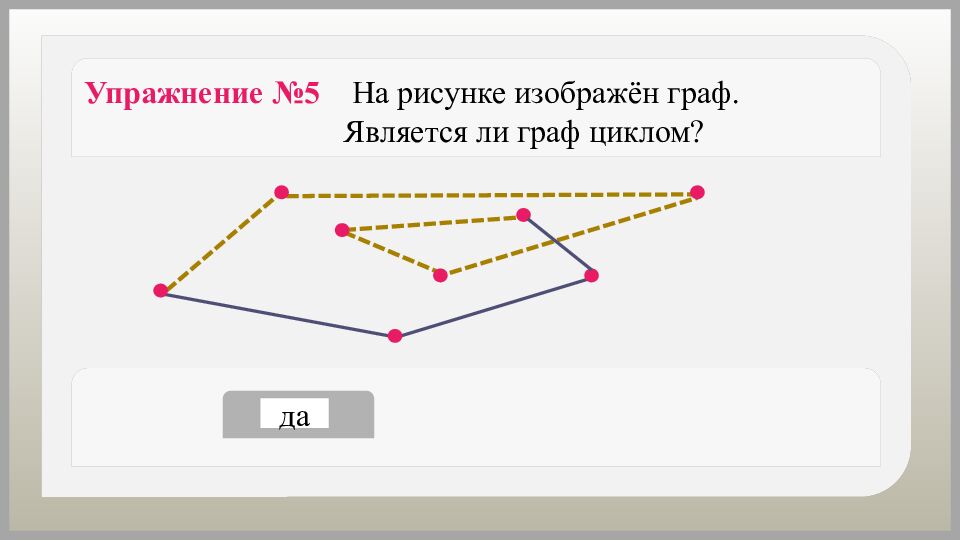
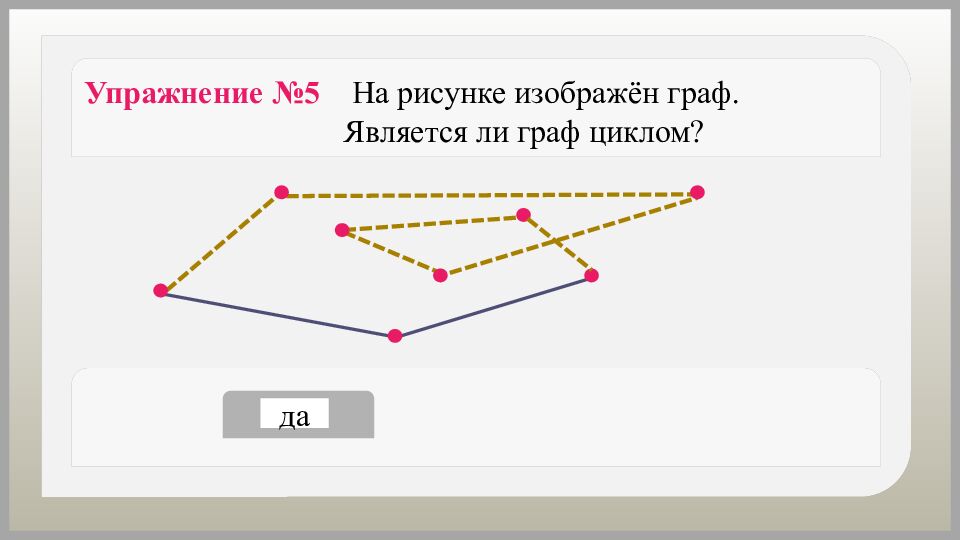
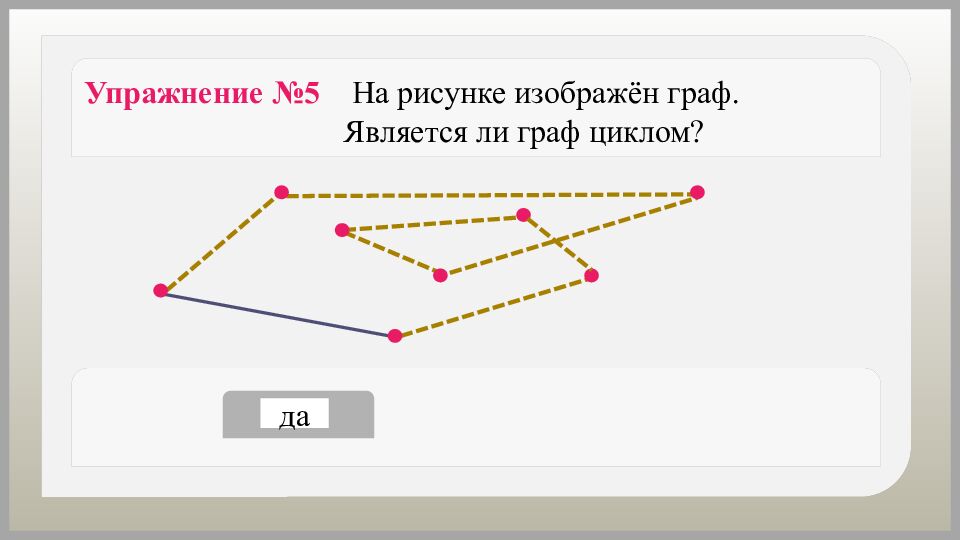
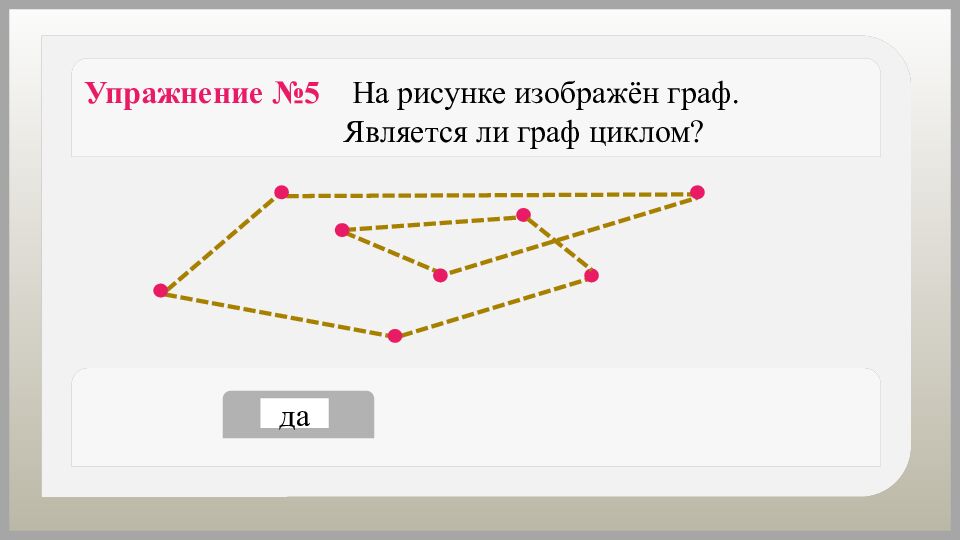
да нет Упражнение №5 На рисунке изображён граф. Является ли граф циклом?
Слайд 47
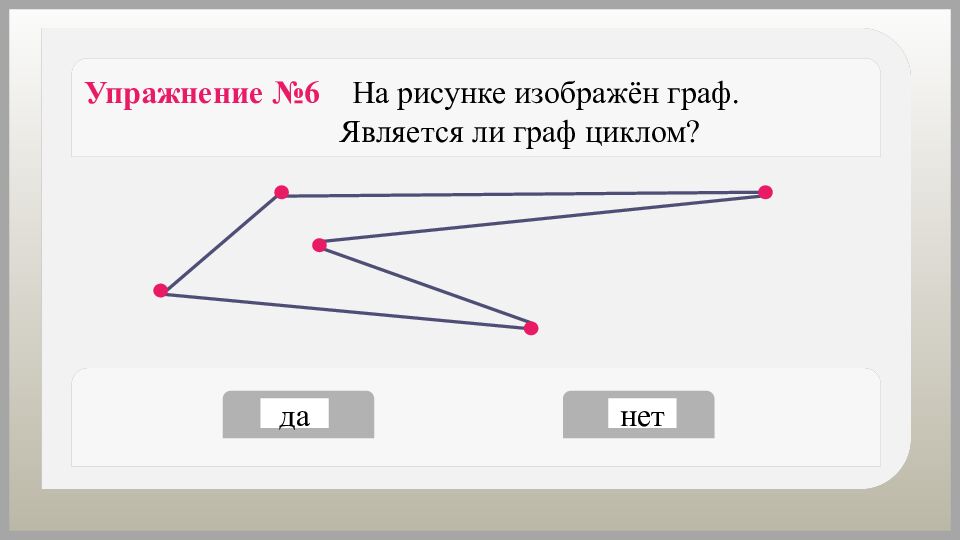
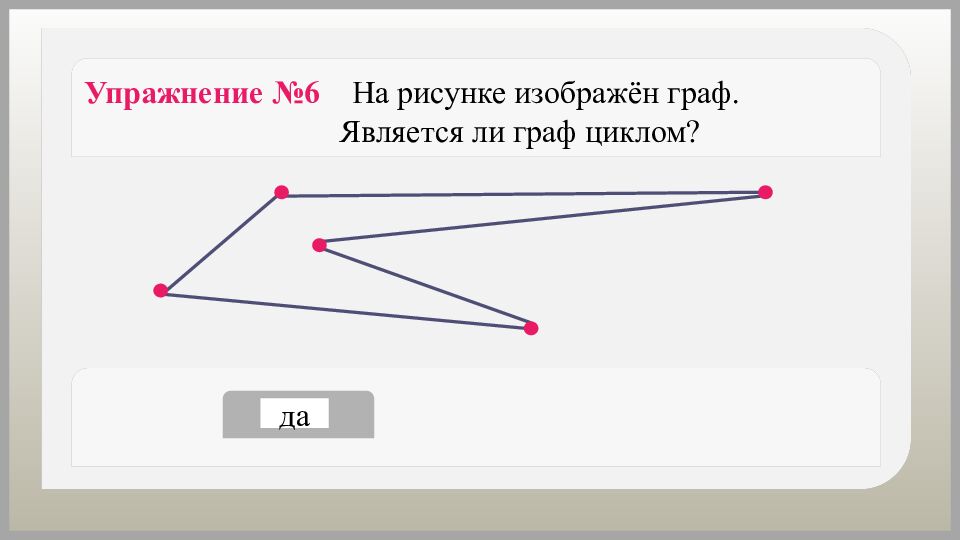
Упражнение №6 На рисунке изображён граф. Является ли граф циклом? да нет
Слайд 49
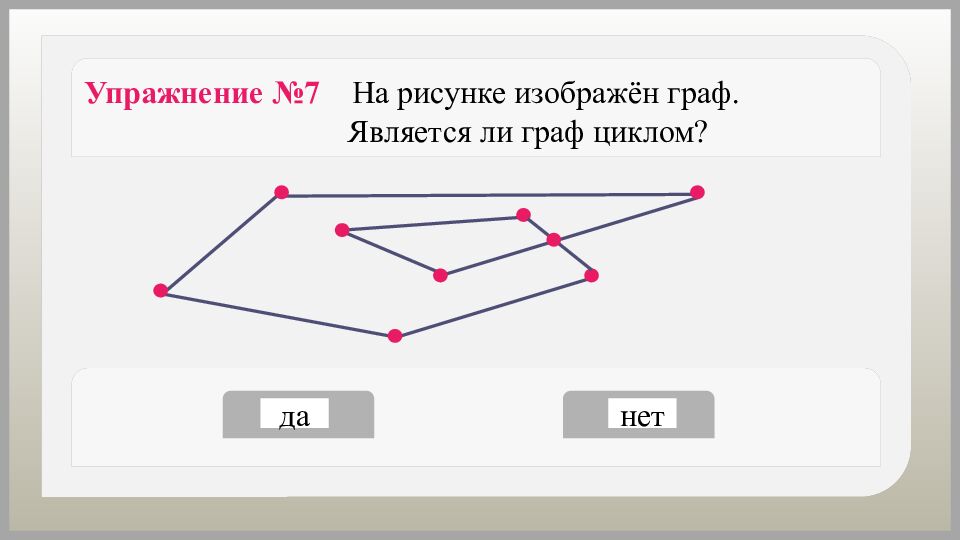
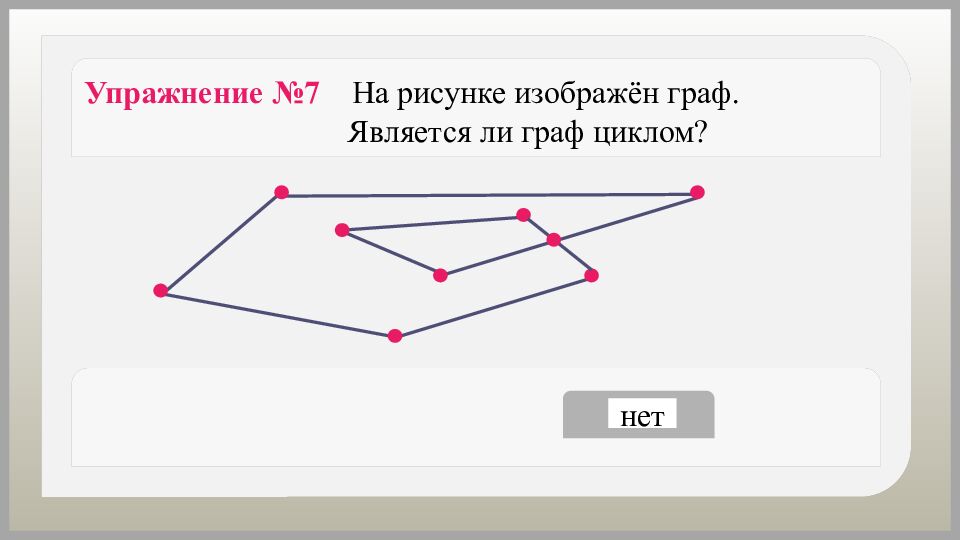
да нет Упражнение №7 На рисунке изображён граф. Является ли граф циклом?
Слайд 51
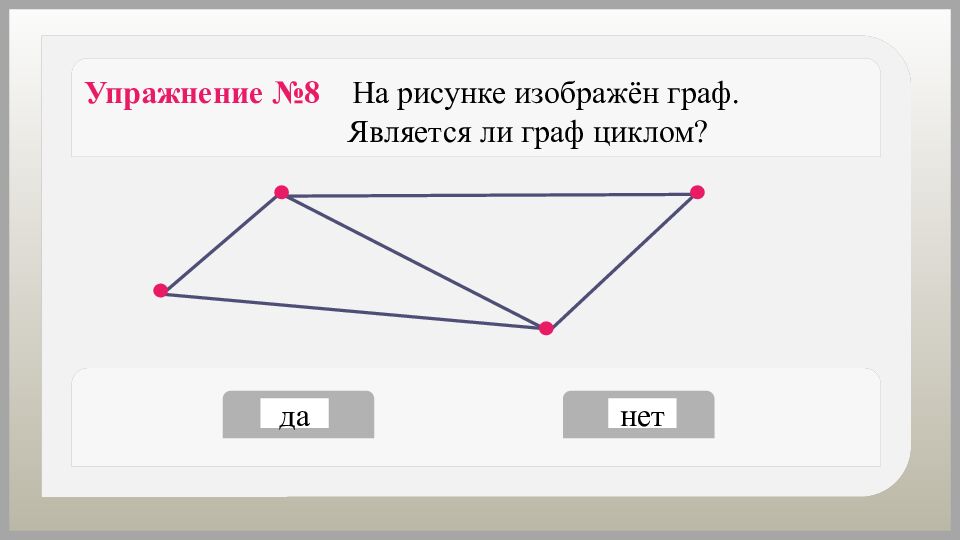
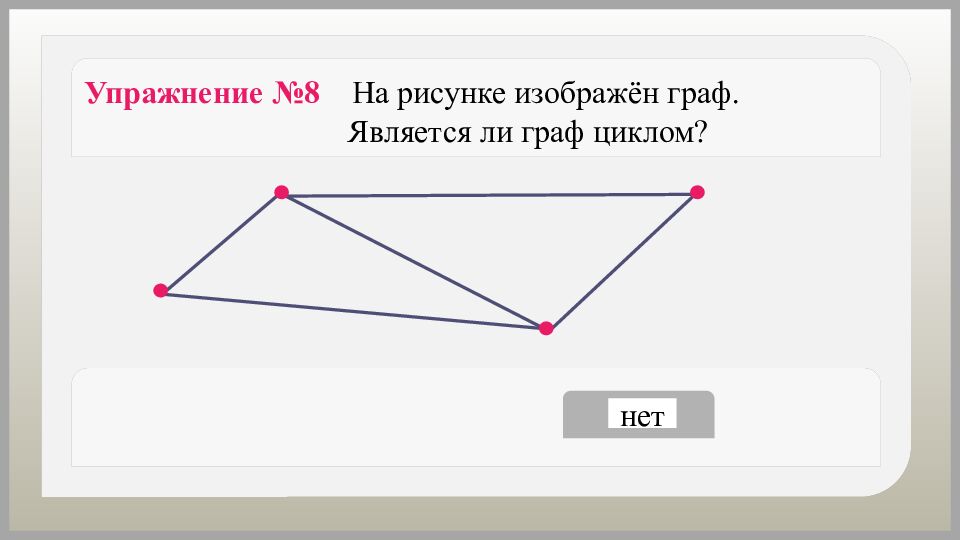
да нет Упражнение №8 На рисунке изображён граф. Является ли граф циклом?
Слайд 53
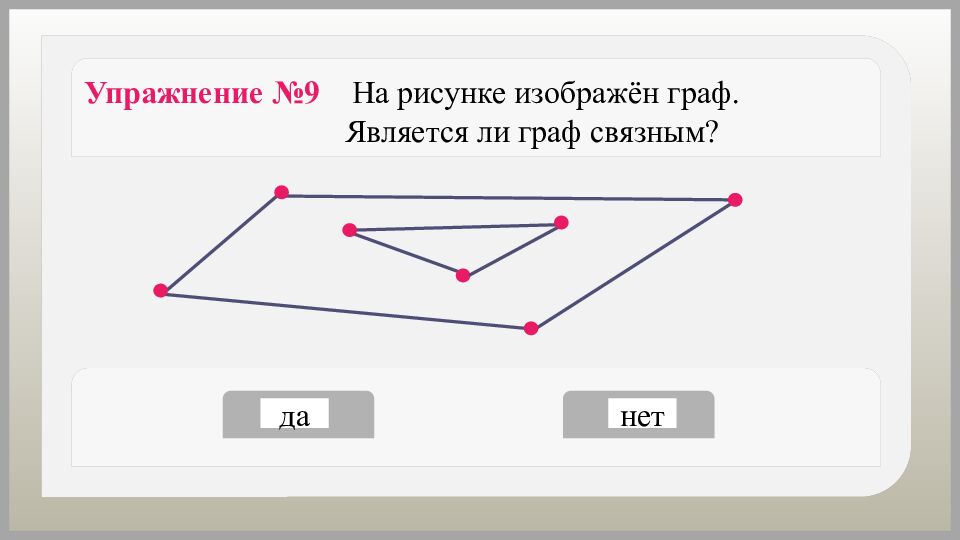
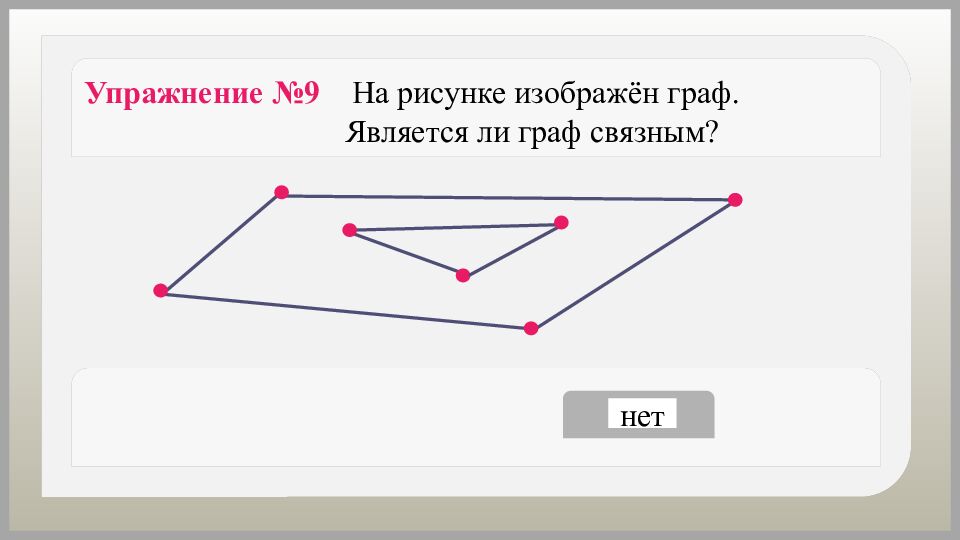
Упражнение №9 На рисунке изображён граф. Является ли граф связным? да нет
Слайд 55
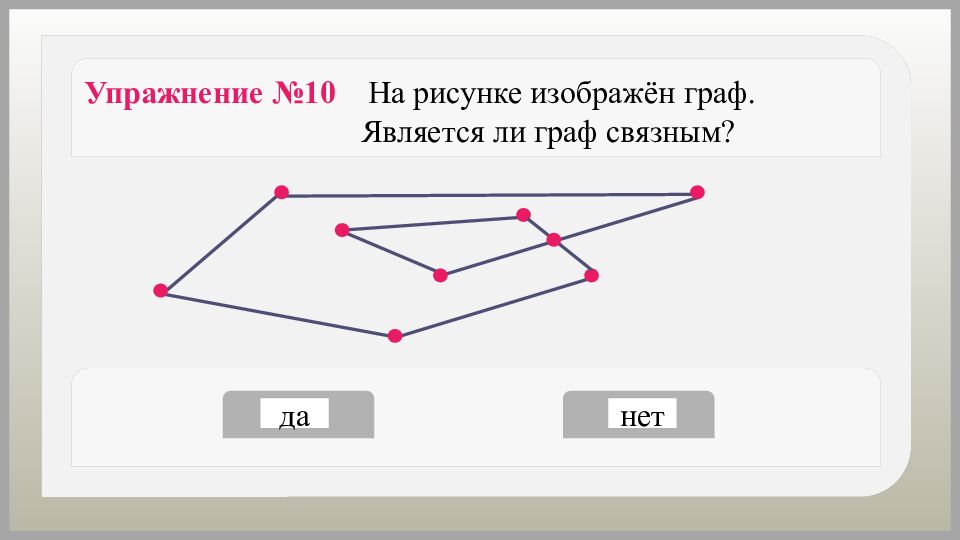
да нет Упражнение №10 На рисунке изображён граф. Является ли граф связным?
Слайд 58
Что такое путь в графе? Что такое цепь в графе (простой путь)? Какой граф называется связным? Что такое цикл в графе?