Студент Группы 6011 Егоров Андрей
Понятие Энтропи́и впервые введено в 1865 Р. Клаузиусом в термодинамике для определения меры необратимого рассеяния энергии. Энтропия применяется в разных отраслях науки, в том числе и в теории информации как мера неопределенности какого-либо опыта, испытания, который может иметь разные исходы. Эти определения энтропии имеют глубокую внутреннюю связь. Так на основе представлений об информации можно вывести все важнейшие положения статистической физики. Информационная двоичная энтропия для независимых ( неравновероятных ) случайных событий x с n возможными состояниями (от 1 до n, p — функция вероятности) рассчитывается по формуле Шеннона : Эта величина также называется средней энтропией сообщения. Энтропия в формуле Шеннона является средней характеристикой – математическим ожиданием распределения случайной величины i1, i2 … in
Например, в последовательности букв, составляющих какое-либо предложение на русском языке, разные буквы появляются с разной частотой, поэтому неопределённость появления для некоторых букв меньше, чем для других. В 1948 году, исследуя проблему рациональной передачи информации через зашумлённый коммуникационный канал, Клод Шеннон предложил революционный вероятностный подход к пониманию коммуникаций и создал первую, истинно математическую, теорию энтропии. Его сенсационные идеи быстро послужили основой разработки теории информации, которая использует понятие вероятности. Понятие энтропии, как меры случайности, введено Шенноном в его статье «A Mathematical Theory of Communication », опубликованной в двух частях в Bell System Technical Journal в 1948 году. В случае равновероятных событий (частный случай), когда все варианты равновероятны, остается зависимость только от количества рассматриваемых вариантов и формула Шеннона значительно упрощается и совпадает с формулой Хартли, которая впервые была предложена американским инженером Ральфом Хартли в 1928 году, как один из научных подходов к оценке сообщений: где I – количество передаваемой информации, p – вероятность события, N – возможное количество различных (равновероятных) сообщений.
1. На любой из позиций двоичного кода может быть с равной вероятностью переданы «0» (отсутствие импульса) и «1» (импульс). Помехи преобразуют «1» в «0» с вероятностью 0,02 и «0» в «1» с вероятностью 0,04. Найти вероятность приема «0» на конкретной позиции кода. Определить вероятность того, что был передан «0», если принят «0».
Х=0 на приемной стороне можно получить при передаче нуля или единицы. B1 - был передан ноль, B2 - была передана единица. Вероятность передачи ноля P(B1) = 0.5. Вероятность передачи единицы P(B2) = 0.5. Событие A - принят ноль. Ноль принят при переданном нуле: P(A/B1) = 1- 0.04= 0.96. Ноль принят при переданной единице: P(A/B2) = 0.02. Используя формулу полной вероятности, найдем вероятность события А: P(A)= P(B1)*P(A/B1)+ P(B2)*P(A/B2)= 0.5*(1- 0.04)+ 0.5*0.02= 0.49. Вероятность того, что был передан 0, если принят 0 найдем по формуле Байеса: P(B1/A)= P(B1)*P(A/B1) / P(A)= 0.5*0.96 / 0.49= 0.9796.
2. Алфавит состоит из букв а, b, с, d. Вероятности появления букв равны соответственно 0,25; 0,25; 0,34; 0,16. Определите количество информации, приходящееся на символ сообщения, составленного с помощью такого алфавита.
Количество информации на символ алфавита есть энтропия данного алфавита. Так как символы алфавита не равновероятны, то энтропия равна:
3. Имеются две системы X и Y, объединяемые в одну, вероятности состояний которой представлены следующей матрицей : Определите полную условную энтропию H(Y/X).
Вычислим безусловные вероятности как суммы совместных вероятностей по строкам и столбцам исходной матрицы. Определим условные вероятности по формуле P ( Y / X ) = P ( X, Y )/ P ( X ) и составим матрицу условных вероятностей. Общая условная энтропия: H(Y/X) = 0,6 (0,333 log 2 0,333 + 0,5 log 2 0,5 + 0,167 log 2 0,167) = 0,87 бит.
4. Вероятности появления символов источника алфавита p ( x 1 )=0.5 p ( x 2 )=0.25 p ( x 3 )=0.125 p ( x 4 )=0.125. Между соседними символами имеются корреляционные связи, которые описываются матрицей вероятностей. Требуется определить избыточность источника при статистической независимости символов и избыточность при зависимости символов.
Для оценки избыточности нужно найти энтропию источника информации H(X) и общую условную энтропию H( Y /X) источника. . H(Y/X) = 0,5 log 2 0,5 + 0,25 log 2 0,25 + 2*(0,125 log 2 0,125) = 1,75 бит / символ. H(Y/X) = 0,5((13/16) log 2 (13/16) + (3/16) log 2 (3/16)) + 0,25((1/8) log 2 (1/8) + (1/2) log 2 (1/2) + (3/8) log 2 (3/8)) + 0,125(1 log 2 1) +0,125((1/2) log 2 (1/2) + (1/4) log 2 (1/4) + (1/4) log 2 (1/4)) = 0,887 бит / символ.
Максимально возможная энтропия источника с четырьмя символами определяется мерой Хартли: H max = log 2 4 = 2 бит/символ. Следовательно, избыточность источника при статистической независимости символов: R1 := 1 – H(X)/ H max ; R1 = 0,125. Избыточность при зависимости символов: R 2 := 1 – H ( Y / X )/ H max ; R 2 = 0,556.
5. Закодировать методом Шенно-Фано блоки «мы все учились понемногу чему-нибудь и как-нибудь». Каково среднее число символов на знак? блок мы все учились понемногу чему нибудь и как - вероятность 0,37 0,13 0,125 0,08 0,06 0,052 0,023 0,11 0,05
Составим таблицу кодов для символов алфавита. Среднее число символов на знак: n ср =2*(0,37+0,13)+3*(0,125+0,11)+4*(0,08+0,06+0,052)+5*(0,05+0,023)=2,838. Блок Вероятность Символы кода Код мы 0,37 0 0 00 все 0,13 1 01 учились 0,125 1 0 0 100 Как 0,11 1 101 Понемногу 0,08 1 0 0 1100 Чему 0,06 1 1101 нибудь 0,052 1 0 1110 - 0,05 1 0 11110 и 0,023 1 11111
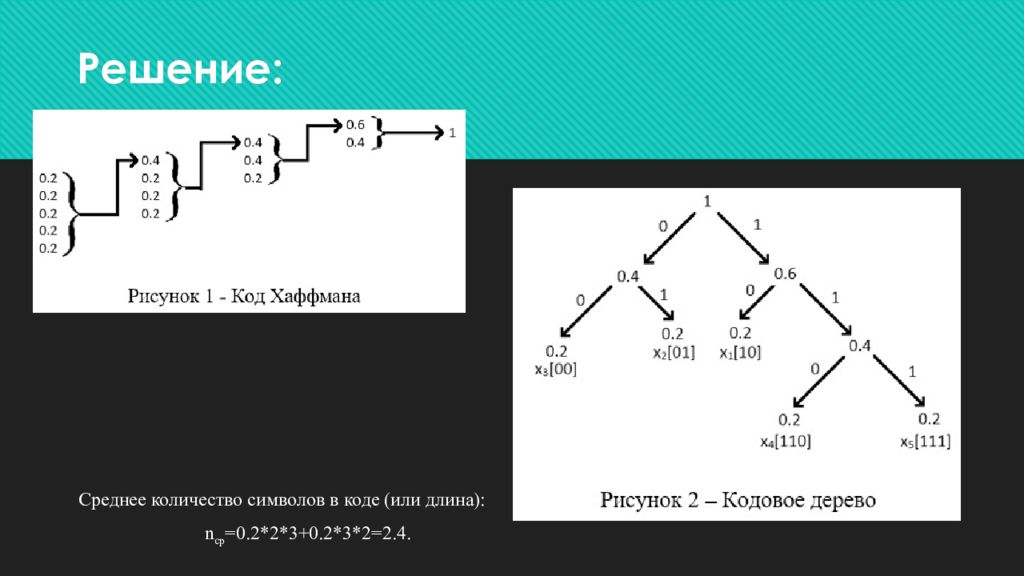
6. Построить код Хаффмана для ансамбля сообщений { x i }, i=1…5 c вероятностями. P ( X ) {0.2 0.2 0.2 0.2 0.2}. Определить характеристики эффективного кода.
Среднее количество символов в коде (или длина): n ср =0.2*2*3+0.2*3*2=2.4.
7. Определить избыточность корректирующего кода при общем числе кодовых комбинаций N =256.
Общее число кодовых комбинаций: N =2 n ( u ) =256. Количество исходных символов: n ( u )= log 2 256=8. n ( u )=8 тогда из таблицы 1 находим n ( k )=4 и n =12. Избыточность помехоустойчивого кода определяем по формуле: Q = n ( k )/ n *100%=4/12*100%=33.3%.
