Решение задач Задача про Красную Шапочку Красная Шапочка идет от домика мамы к домику бабушки. Красная Шапочка может идти только по дорожкам слева направо. Схема дорожек показана на рисунке. Дорожки Красная Шапочка выбирает наудачу. На двух дорожках девочку поджидают Волки. Найдите вероятность того, что Красная Шапочка на своем пути: а ) встретит ровно одного Волка ; б) встретит двух Волков; в ) не встретит ни одного Волка ; г) встретит хотя бы одного Волка. Решение Всего у Красной Шапочки вариантов путей от домика мамы до домика бабушки: 3∙4=12 а) Одного волка можно встретить на маршрутах: 1а, 1б, 1с, 2д, 3д – всего 5 вариантов Следовательно, Р(А)=5/12 б) Двух волков она встретит на маршруте: 1д Следовательно, Р(А)=1/12 в) Не встретит ни одного волка на маршрутах: 2а, 2б, 2с, 3а, 3б, 3с Следовательно, Р(А)=6/12=1/2 г) В данном пункте нас устроят варианты, что Красная Шапочка встретит одного волка, но также и двух. Это 5+1=6 вариантов, т. е. сумма вариантов пунктов а и б. Следовательно, Р(А)=6/12=1/2 Ответ: а) 5/12; б) 1/12; в) 1/2; г) 1/2
Противоположные события. Событием, противоположным событию A, называют событие, которому благоприятствуют все элементарные события, не благоприятствующие событию A. Событие, противоположное событию A, обозначают Поэтому события A и называют взаимно противоположными или дополнениями друг для друга. Пример 1. Бросают игральную кость. Рассмотрим событие A «выпало число, большее 4». Этому событию благоприятствуют элементарные события «выпала пятерка» и «выпала шестерка». Не благоприятствуют событию A следующие элементарные события: «выпала единица», «выпала двойка», «выпала тройка», «выпала четверка». Для события A противоположным событием является событие: «выпало число, меньшее или равное четырем». Событие A Взаимно противоположные события одновременно произойти не могут, но какое-либо из них происходит обязательно. Поэтому P(A)+P( ) = 1. Иными словами, сумма вероятностей взаимно противоположных событий равна единице. Следовательно, P(A) = 1− P( ) и P( ) = 1−P(A). Из этих формул следует, что для вычисления P(A) достаточно знать P( ). Это свойство во многих случаях оказывается полезным. Событие P(A) = P( ) = P(A)+P( ) = + = 1.
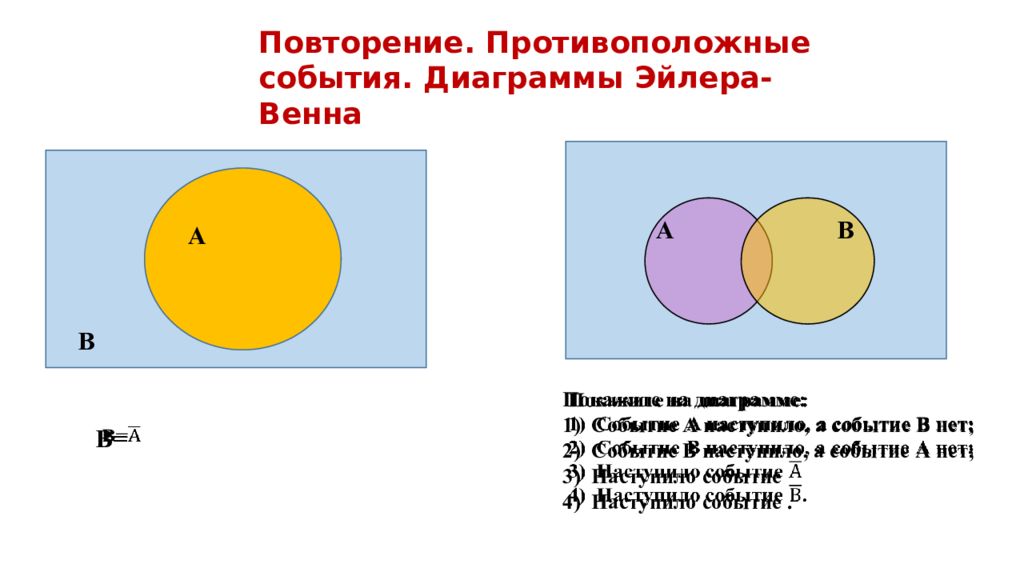
Повторение. Противоположные события. Диаграммы Эйлера-Венна А В А В В= Покажите на диаграмме: Событие А наступило, а событие В нет; Событие В наступило, а событие А нет; Наступило событие Наступило событие.
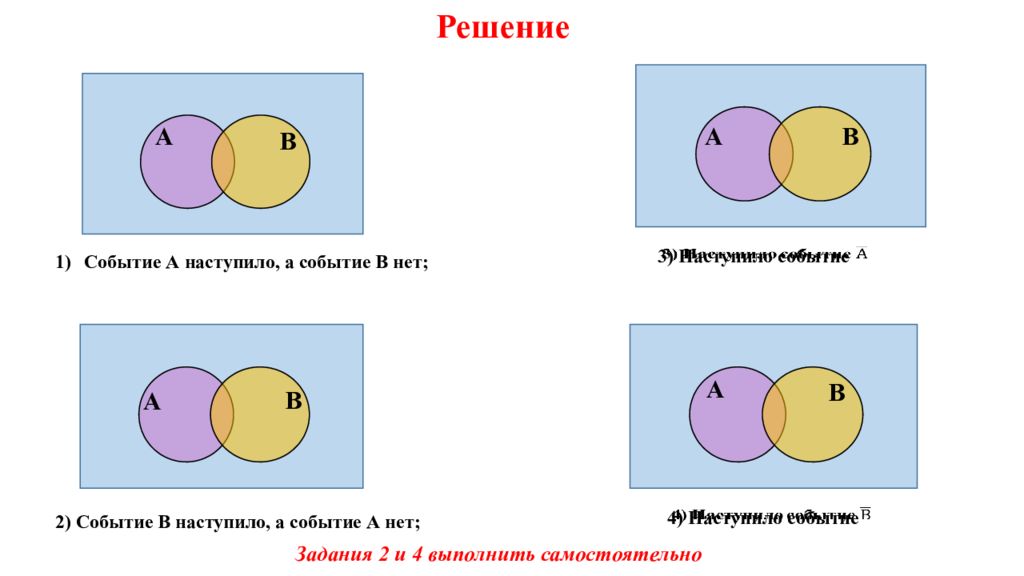
Решение А А А А В В В В Событие А наступило, а событие В нет; 2) Событие В наступило, а событие А нет; 3) Наступило событие 4) Наступило событие Задания 2 и 4 выполнить самостоятельно
Решение задач Задача. Вероятность попадания в мишень стрелком равна 0,6. Какова вероятность того, что он, выстрелив по мишени, промахнется? Решение А – событие «Стрелок попал в мишень» В – событие «Стрелок не попал в мишень» А и В это противоположные события, следовательно, Р(А)+Р(В)=1 Р(В)=1-0,6=0,4 Ответ: 0,4.
Решение задач Задача. Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0,19. Покупатель в магазине выбирает одну такую ручку. Найдите вероятность того, что эта ручка пишет хорошо. Решение Ответ: 0,81. А – событие «Ручка пишет плохо» В – событие «Ручка пишет хорошо» А и В это противоположные события, следовательно, Р(А)+Р(В)=1 Р(В)= 1-0,19=0,81 P(A)+P( ) = 1.
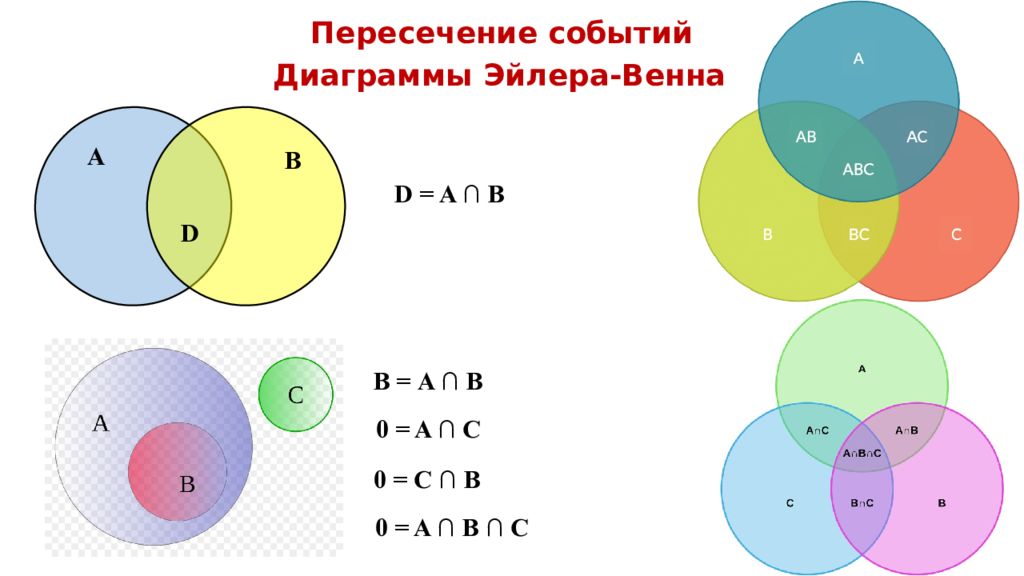
Пересечение событий А В D Диаграммы Эйлера-Венна В = A ∩ B D = A ∩ B 0 = A ∩ B ∩ С 0 = A ∩ С 0 = С ∩ B
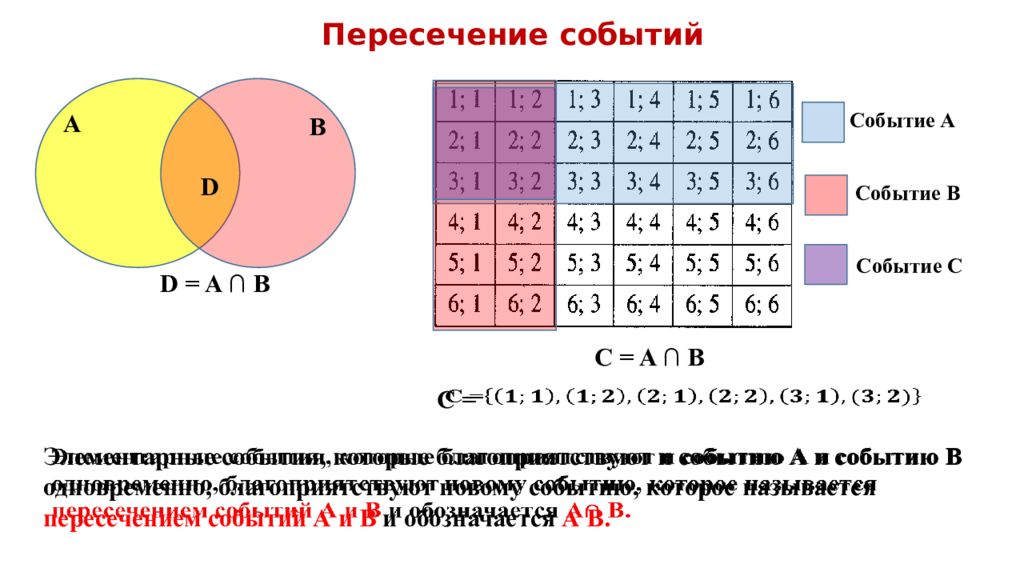
Пересечение событий C обытие А C обытие В C обытие С А В D D = A ∩ B C = A ∩ B C = Элементарные события, которые благоприятствуют и событию А и событию В одновременно, благоприятствуют новому событию, которое называется пересечением событий А и В и обозначается А В.
Объединение событий Диаграммы Эйлера-Венна А С В D = А В С В D = А С
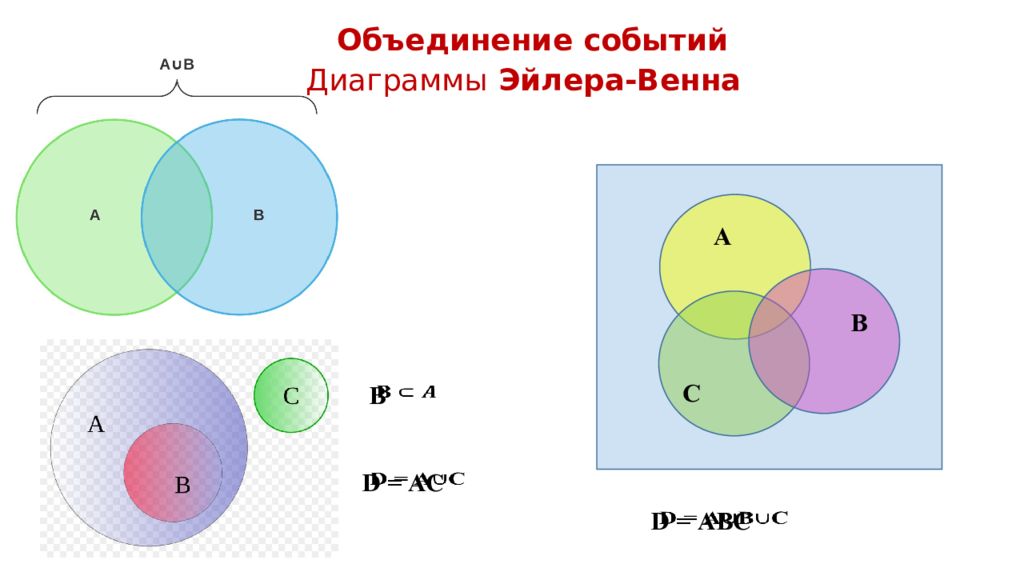
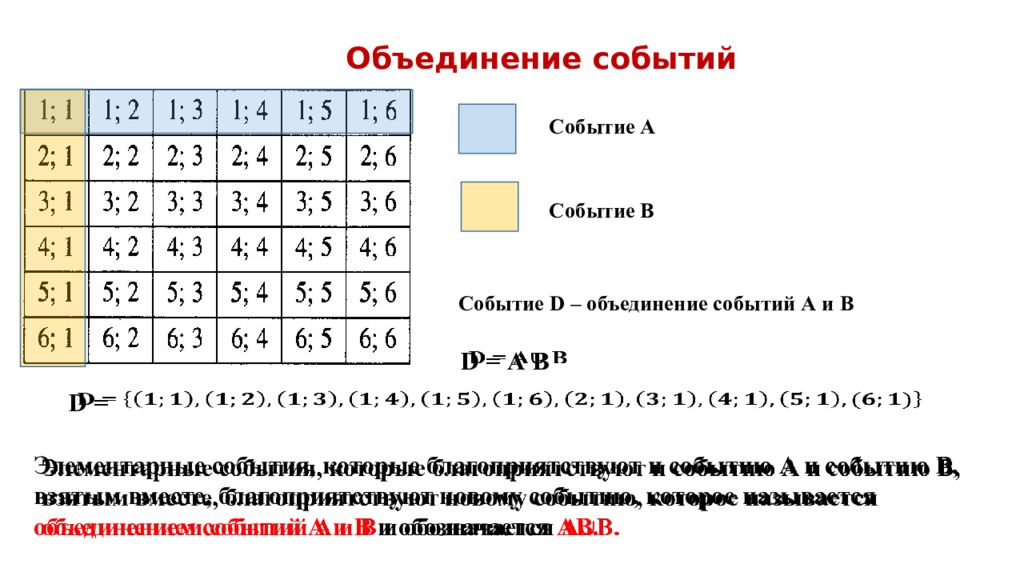
Объединение событий D = А В C обытие D – объединение событий А и В C обытие В C обытие А D = Элементарные события, которые благоприятствуют и событию А и событию В, взятым вместе, благоприятствуют новому событию, которое называется объединением событий А и В и обозначается А В.
Пересечение событий A и B : Объединение событий A и B : Рассмотрим такие события: событие C — «наступило A, но не наступило B» и событие D — «наступило B, но не наступило A ». На диаграмме видно, что события C и A∩B несовместны, поскольку соответствующие фигуры не имеют общих точек. Вместе эти события образуют событие A. Поэтому по правилу сложения вероятностей для несовместных событий находим: P(A ) = P(C)+P(A∩B). Точно так же получаем P(B) = P(D)+P(A∩B). Сложив эти равенства почленно, получим P(A)+P(B) = P(C)+P(D)+P(A∩B )+P(A∩B). События C, D и A∩ B несовместны и образуют событие A∪B. Получаем формулу P(A)+P(B) = P(A∪B) +P(A∩B), откуда P(A∪B) = P(A)+P(B)−P(A∩B). Выведенная формула справедлива для любых событий. Вероятность объединения двух событий равна сумме их вероятностей минус вероятность пересечения. А A B С D В Воспользуемся диаграммой Эйлера и изобразим два события A и B, у которых есть общие благоприятствующие элементарные события. Такие события не являются несовместными. A B A B Формула сложения вероятностей
Несовместные события Задача. На экзамене по геометрии школьнику достается один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему: «Вписанная окружность», равна 0,1. Вероятность того, что это вопрос на тему «Тригонометрия», равна 0,35. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем. Решение Ответ: А – событие «Достался вопрос по теме «Вписанная окружность», Р(А)= В – событие «Достался вопрос по теме «Тригонометрия», Р(В)= А и В – события несовместные, так как по смыслу задачи в билетах нет вопросов, относящихся к двум темам одновременно, следовательно, Р(А В )=Р(А)+Р(В ) Р(А В)=Р(А ) Р(В)=0,1 0,35=0,45
Формула для решения задач P(A∪B) = P(A)+P(B)−P(A∩B).
Решение задач Задача. Вероятность того, что по дороге из школы домой вы встретите черную кошку, равна 0,1. А вероятность того, что по дороге из школы домой вы встретите злую собаку, равна 0,4. Вероятность того, что вам встретятся и черная кошка и злая собака равна 0,04. Найдите вероятность того, что вам встретится хотя бы одно из этих животных. Решение Ответ: Данные события совместные и, следовательно, вероятность того, что вам встретится хотя бы одно из этих животных можно вычислить по формуле: P(A∪B) = P(A)+P(B)−P(A∩B). Значит, P(A∪B) = P(A)+P(B)−P(A∩B ) = 0,1+0,4-0,04 = 0,5-0,04 = 0,46 A B А В
Независимые события Событие В называют независимым от события А, если появление события А не изменяет вероятности появления события В. Пример 1. При бросании кубика вероятность появления числа 2 при втором броске не зависит от первого бросания. Пример 2. Например, если в цехе работают две автоматические линии, по условиям производства не взаимосвязанные, то остановка одной линии не влияет на работу другой. Эти события независимые. В таких случаях говорят, что события независимые и вероятность можно найти по формуле Р(А В) = Р(А) ∙ Р(В) Задача. Дважды бросается игральный кубик. Какова вероятность того, что оба раза выпадет число 5. А – событие «Первый раз выпало число 5», Р(А)= В – событие «Второй раз выпало число 5 », Р(В)= А, В – события независимые, следовательно, Р(А В)= =Р(А)∙ Р(В) Р(А В ) = Р(А) Р(В) = = Решение Ответ:
Правило умножения Задача. За офисом наблюдают две независимые друг от друга видеокамеры. Вероятность того, что в течение суток первая видеокамера выйдет из строя равна 0,001, а вероятность того, что выйдет из строя вторая, равна 0,0005. Найдите вероятность того, что в течение суток выйдут из строя обе видеокамеры. А – событие «Первая вышла из строя» В – событие «Вторая вышла из строя» А, В – события независимые, следовательно, Р(А В ) = Р(А) Р(В) =0,001 0,0005=0,0000005= 5 10⁻⁷ Ответ: 5 10 ⁻⁷ Решение Р(А В)=Р(А) ∙ Р(В)
Решение задач Задача. Вероятность остановки за смену одного станка, работающего в цехе, равна 0,15, а другого – 0, 16. Какова вероятность того, ч то оба станка за смену не остановятся ? А – событие «Первый вышел из строя», Р(А)=0,15 -- событие «Первый не остановится», Р( ) = 1 – 0,15 = 0,85 В – событие «Второй вышел из строя», Р(В)=0,16 -- событие «Второй не остановится», Р( ) = 1 – 0,16 = 0,84 и – события независимые, следовательно, Р(А В) = Р(А) ∙ Р(В) Р( ) = Р( ) Р( ) = 0,85 0,84 = 0,714 Решение Ответ: 0,714 P(A)+P( ) = 1
Задача. В магазине три продавца. Каждый из них занят с клиентом с вероятностью 0,6. Найдите вероятность того, что в случайный момент времени все три продавца заняты одновременно(считайте, что клиенты заходят независимо друг от друга). Решение Ответ: 0,216. А – событие «Первый занят с клиентом» В – событие «Второй занят с клиентом » С – событие «Третий занят с клиентом » Р(А )=Р(В)=Р(С)=0,6 Событие «Все три продавца заняты одновременно»: Р(А) Р(В) Р(С) А, В, С – события независимые, следовательно, Р(А) Р(В) Р(С) = Р(А) Р(В) Р(С) =0,6 0,6 0,6=0,216 Решение задач
Домашняя работа 1. В фирме такси в наличии 50 легковых автомобилей; 27 из них чёрного цвета с жёлтыми надписями на бортах, остальные — жёлтого цвета с чёрными надписями. Найдите вероятность того, что на случайный вызов приедет машина жёлтого цвета с чёрными надписями. 3*. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что выпадет хотя бы две решки. 2. В среднем из 300 садовых насосов, поступивших в продажу, 60 подтекают. Найдите вероятность того, что случайно выбранный для контроля насос подтекает.
