Учитель математики МБОУ «Лицей № 35 им. А.И. Герлингер» Доманова Наталья Сергеевна Г. Новокузнецк
История возникновения теории вероятности Теория вероятностей - это математическая наука, изучающая закономерности в массовых случайных явлениях. Первооткрывателями этой теории считаются Блез Паскаль (1623 -1662), Пьер Ферма (1601 -1665) и голландский ученый Христиан Гюйгенс (1629 -1695)
История возникновения теории вероятности Во второй половине Х IX века основополагающий Вклад в теорию вероятностей внесли русские учёные Панфутий Львович Чебышёв (1821 -1894) и его ученик Андрей Андреевич Марков (1856 -1922) В XX веке исследования Чебышёва и Маркова продолжили Александр Яковлевич Хинчин, Андрей Николаевич Колмагоров и др. ЗАКОН БОЛЬШИХ ЧИСЕЛ
История возникновения теории вероятности Андрей Николаевич Колмогоров (1903 – 1987) был выдающимся ученым, внесшим большой вклад во многие разделы математики и её приложений. Много внимания уделял Андрей Николаевич проблемам школьного математического образования. Им была основана школа – интернат физико – математического профиля при МГУ для способных школьников страны. Теперь эта школа носит имя А.Н. Колмагорова.
Что такое событие? В результате бросания любой монеты ( это испытание ) обязательно произойдет одно из двух событий : выпала «решка» или выпал «орел». Опыт, эксперимент, наблюдение явления или некоторого процесса называется испытанием. Испытания сопровождаются их исходами (событиями). Событие — это качественный и (или) количественный результат испытания (исход), осуществляемого при определённой совокупности условий.
Виды событий СОБЫТИЕ Достоверное Событие, которое при данных условиях ОБЯЗАТЕЛЬНО наступит Случайное Событие, которое при данных условиях может наступить, а может и не наступить Невозможное Событие, которое при данных условиях НИКОГДА не наступит !!! !?! ? ! ? ? ! !
Достоверное событие Случайное событие Невозможное событие Среда наступит после вторника В следующий четверг пойдет снег Четверг наступит после пятницы Градусная мера острого угла равна 37 градусам Бросили два игральных кубика. Сумма выпавших очков равна 3 В феврале 30 дней Бросили два игральных кубика. Сумма выпавших очков оказалась меньше 13; Задумали четное число. Число делится на 5 Бросили два игральных кубика. Сумма выпавших очков меньше 2 Градусная мера прямого угла 90 градусов Задумали нечетное число. Число делится на 3 Градусная мера тупого угла 92 градуса Виды событий Заполните таблицу: Четверг наступит после пятницы; Среда наступит после вторника; В следующий четверг пойдет снег; В феврале 30 дней; Градусная мера острого угла равна 37 градусам; Бросили два игральных кубика. Сумма выпавших очков оказалась меньше 13; Бросили два игральных кубика. Сумма выпавших очков равна 3; Бросили два игральных кубика. Сумма выпавших очков меньше 2; Градусная мера прямого угла 90 градусов; Задумали четное число. Число делится на 5; Задумали нечетное число. Число делится на 3; Градусная мера тупого угла 92 градуса. Достоверное событие Случайное событие Невозможное событие
Равновозможные события Равновозможные события – это события, которые имеют одинаковую возможность появления Появление «орла» и появление «решки» при о дном бросании монеты При бросании игральной к ости появление каждой из её граней Появление карты определённой м асти при изъятии одной к арты из колоды
Что такое вероятность события? Для обозначения событий используются большие буквы латинского алфавита: А, В, С и т.д. Событие А – выпала «решка» Событие В – выпал «орёл» Пример. Вероятностью события А называют отношение количества случаев, БЛАГОПРИЯТСТВУЮЩИХ событию А, к числу всех РАВНОВОЗМОЖНЫХ случаев, один из которых обязательно произойдет. Р(А)= m/n, где Р(А) –вероятность события А, m - количество БЛАГОПРИЯТСТВУЮЩИХ случаев, n - количество РАВНОВОЗМОЖНЫХ случаев.
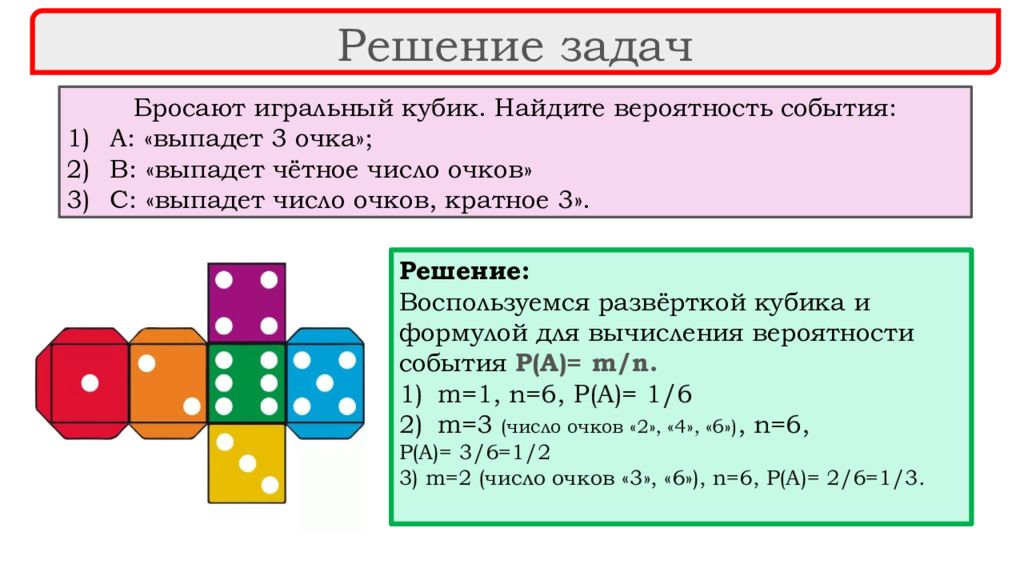
Решение задач Бросают игральный кубик. Найдите вероятность события: А: «выпадет 3 очка»; В: «выпадет чётное число очков» С: «выпадет число очков, кратное 3». Решение: Воспользуемся развёрткой кубика и формулой для вычисления вероятности события Р(А)= m/n. m=1, n=6, P(A)= 1/6 m=3 ( число очков «2», «4», «6»), n=6, P(A)= 3/6=1/2 3) m= 2 ( число очков «3», «6»), n=6, P(A)= 2 /6=1/ 3.
Решение задач На четырёх карточках написали буквы М, Р, Е, О. Положили карточки на стол буквами вниз в произвольном порядке. Какова вероятность того, что после переворачивания карточек получится слово МОРЕ? Решение: Используем формулу Р(А)= m/n, А –событие, что получится слово МОРЕ. Имеем m =1, найдем n, составим для этого дерево возможных вариантов: М О Е Р О Р М Е О Е О Р М Е Р М Р Е М Р О О М Р М Е М Е Р Р М Е Е О М О Е Р О О О Р М О Р М Р Е Е М М Р О Е О М М Е Е Р О Е Р О n = 24 Находим вероятность Р(А)= 1/24.
Решение задач В среднем из 150 карманных фонариков, поступивших в продажу, шесть неисправных. Найдите вероятность того, что выбранный наудачу в магазине фонарик окажется исправен. ( Открытый банк заданий ОГЭ ФИПИ) У бабушки 20 чашек: 6 с красными цветами, остальные с синими. Бабушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с синими цветами. (Открытый банк заданий ОГЭ ФИПИ ) Решение: Воспользуемся формулой для вычисления вероятности события Р(А)= m/n. А –событие, что фонарик окажется исправным. m=1 50- 6 =144, n= 150, P(A)= 1 44 / 150=72/75 =24/25. Решение: Воспользуемся формулой для вычисления вероятности события Р(А)= m/n. А –событие, что чай бабушка нальёт в чашку с синими цветами. m = 20- 6 =14, n= 20, P(A)= 1 4 / 20=7/10.
ОДЗ: (x-4)(x+1)<0 -1<x<4 - 2 Замена: (t-2)(t-5)>0 t<2 t>5 Возврат к замене: 3x- X<0 x>3 С ОДЗ: x (-1 ;0) (3;4) t>5 Возврат к замене: 32 Решения нет Ответ: x (-1 ;0) (3;4)
Элементы комбинаторики Для понимания основ данного предмета необходимы некоторые сведения из теории соединений. Напомним основополагающие определения из теории соединений, называемой также комбинаторикой.
Если вероятность события А зависит от того, произошло событие В или нет, то говорят об условной вероятности события А и обозначают ее P(A/B). В противном случае говорят, что А независимо от В.
Задание № 1. Стрелок попадает в цель в среднем в 8 случаях из 10. Какова вероятность, что, сделав три выстрела, он ни разу не попадет? a ) 0,08 b ) 0,4 c ) 0,6 d ) 0,008 Задание № 2 Для посева берут семена из двух пакетов. Вероятность прорастания семян в первом пакете равна 0,4, а во втором 0,5. Взяли по одному семени из каждого пакета, тогда вероятность того, что оба они прорастут, равна: a) 0,9 b ) 0,45 c ) 0,3 d ) 0,2 Задание № 3 Вероятность того, что в этом году будет хороший урожай апельсинов, равна 0,9, а лимонов – 0,7. Тогда вероятность того, что уродятся и апельсины, и лимоны, равна: a ) 0,8 b ) 0,3 c ) 0,63 d ) 0,5 Задание № 4. Вероятность взять бракованную деталь из первого ящика равна 0,2, а из второго – 0,3. Из каждого ящика взяли по одной детали. Тогда вероятность того, что обе они бракованные, равна: a ) 0,06 b ) 0,5 c ) 0,25 d ) 0,1 Задание № 5Станок-автомат производит изделия трех сортов. Первого сорта – 80%, второго – 15%. Чему равна вероятность того, что наудачу взятое изделие будет или второго, или третьего сорта? 0,2 b ) 0,95 c ) 0,8 d ) 0,15 Задание № 6Два стрелка стреляют по разу в общую цель. Вероятность попадания в цель у одного стрелка 0,8, у другого – 0,9. Найти вероятность того, что цель не будет поражена ни одной пулей. 0,2 b ) 0,02 c ) 0,3 d ) 0,15 Задание № 7 Стрелок попадает в цель в среднем в 8 случаях из 10. Какова вероятность, что, сделав три выстрела, он хотя бы раз попадёт в цель? a ) 0,999 b ) 0,992 c ) 0,92 d ) 0,8 Задание № 8) Два стрелка стреляют по мишени. Вероятность попадания в цель у одного стрелка 0,7, у другого – 0,8. Найти вероятность того, что цель будет поражена. Варианты ответов: a) 0,75 b ) 0,8 c ) 0,56 d ) 0,94
Ответы: № задания В1 В2 В3 В4 В5 В6 1 d b b a c d 2 d c a c d b 3 c b d b c b 4 a d d b a c 5 a d d c b a 6 b a c a b b 7 b a c a c d 8 d a b d b a
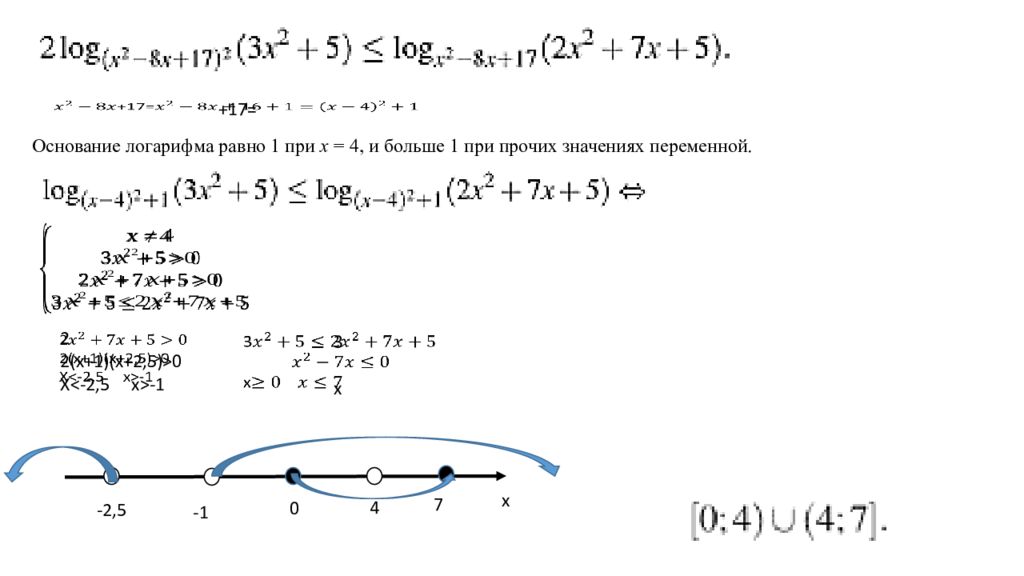
+17= Основание логарифма равно 1 при х = 4, и больше 1 при прочих значениях переменной. 2 2(x+1)(x+2,5)>0 X<-2,5 x>-1 3 x -2,5 -1 0 4 7 x
Благодарю за внимание!
