Первый слайд презентации: Решение заданий типа №15, №16 ОГЭ
“ Мало иметь хороший ум, главное – хорошо его применять. ” Р. Декарт
Слайд 2: Теория
Задание №6. Основы геометрии. Чаще всего встречаются задания на решение треугольников, но знать надо все фигуры планиметрии. Необходимые знания: виды треугольников; понятия биссектрисы, медианы, высоты; тригонометрические функции и их значения; основное тригонометрическое тождество; формулы приведения; теорема Пифагора. И помните при правильном решении ответ получается точно без корня.
выпускник чаще всего может перепутать катет с гипотенузой; выпускник чаще всего не знает или неверно записывает отношение сторон при использовании тригонометрических функций;
Слайд 4: Задания для решения
Задача 1 Задача 2 Задача 3 задача 5 Задача 4 Задача 6 Задача 7 Задача 8 Задача 9*
Слайд 5: Задача 1
В равнобедренном треугольнике ABC c основанием AC боковая сторона АВ равна 15,а высота, проведенная к основанию, равна 9. Найдите косинус угла А.
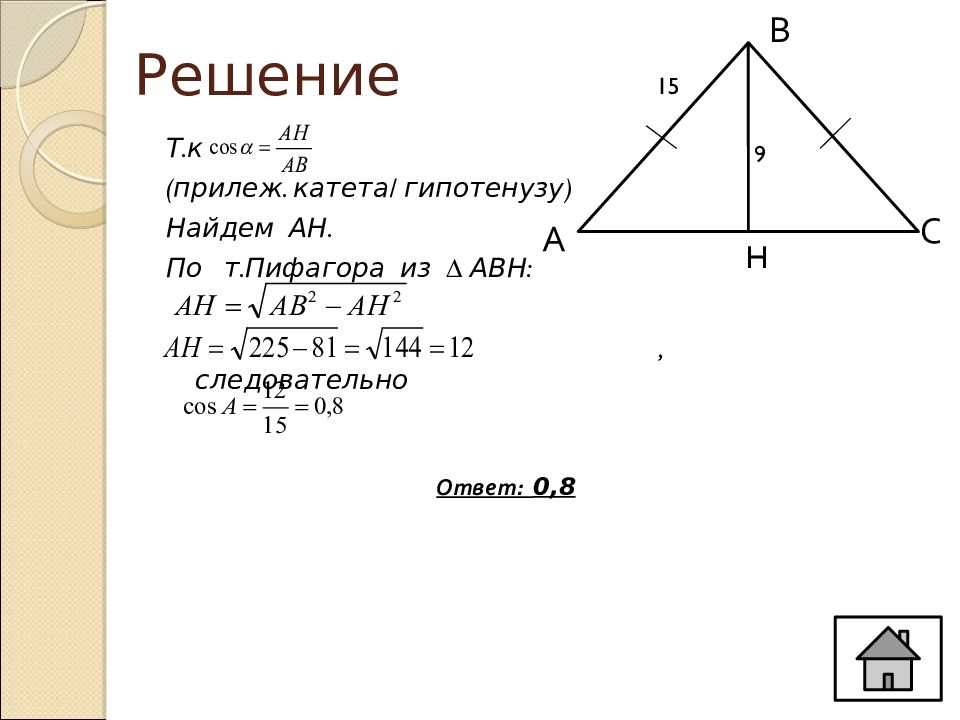
Слайд 6: Решение
Т.к (прилеж. катета/ гипотенузу) Найдем АН. По т.Пифагора из ∆ АВН: , следовательно А С В H 15 9 Ответ: 0,8
Слайд 8: Решение
А В С Нам известен прилежащий катет, следовательно зная синус угла А можно найти его косинус. По основному тригонометрическому тождеству: По определению косинуса: ; Ответ: 28
Слайд 10: Решение
А В С Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе. Следовательно Найдем отрезок АС из ∆ АВС: Отсюда Ответ: 0,6
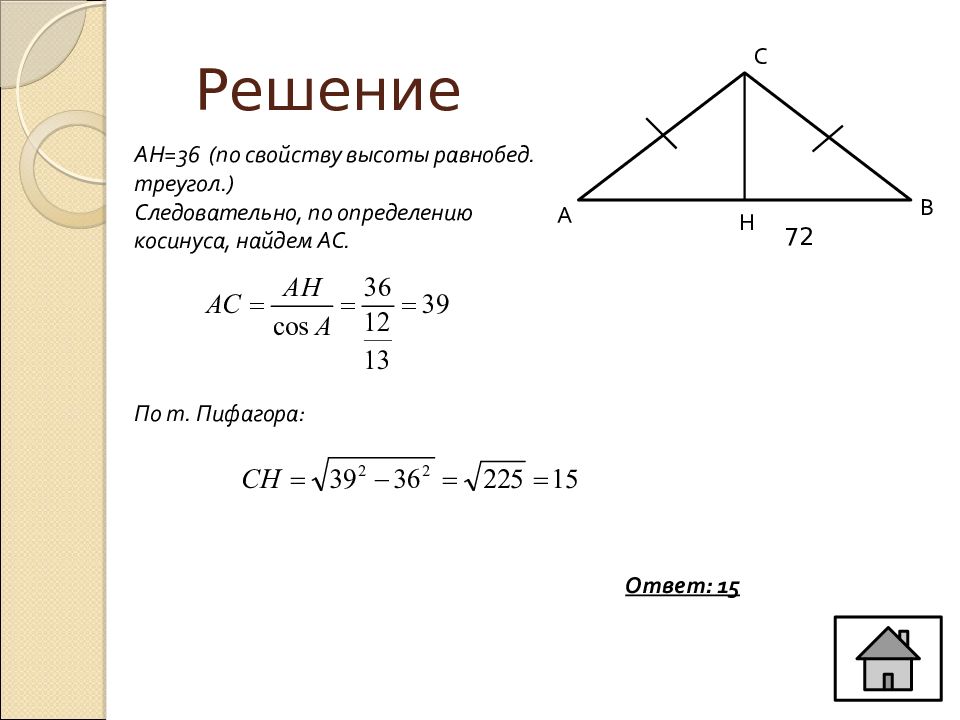
Слайд 12: Решение
С В А 72 Н АН=36 (по свойству высоты равнобед. треугол.) Следовательно, по определению косинуса, найдем АС. По т. Пифагора: Ответ: 15
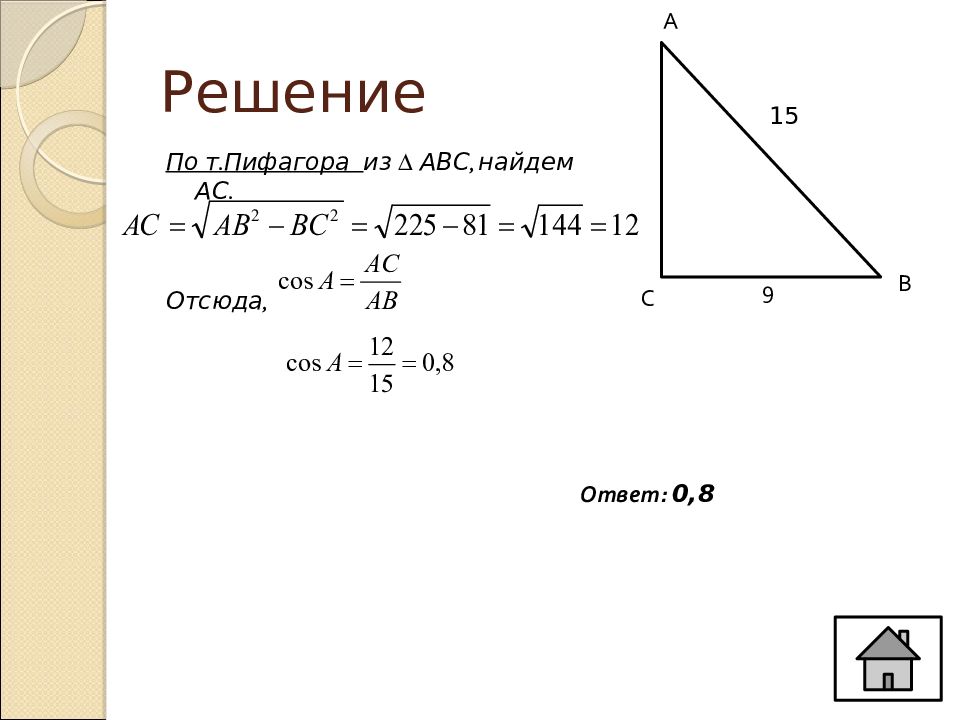
Слайд 14: Решение
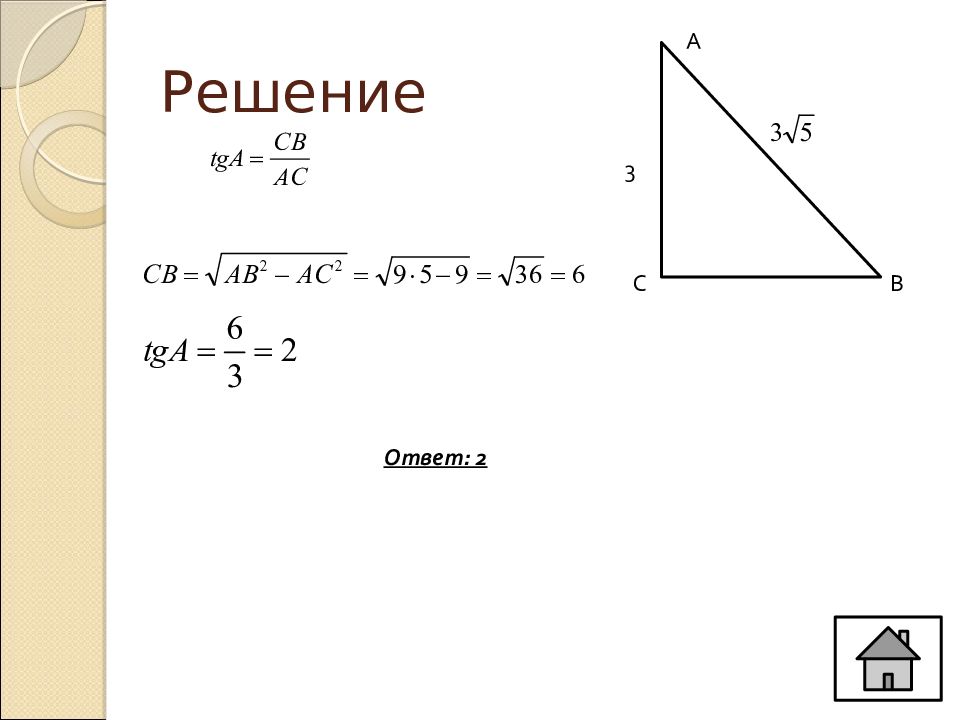
По т.Пифагора из ∆ АВС, найдем АС. Отсюда, С А В 15 9 Ответ: 0,8
Слайд 17: Задача 7
В треугольнике АВС угол С равен 90, СН - высота,ВС=10, СН=. Найти sinA.
Слайд 18: Решение
А В С Н 10 Т.к. Из НВС по т.Пифагора найдем НВ: По свойству высоты СН: АВ=100, следовательно Ответ: 0,1
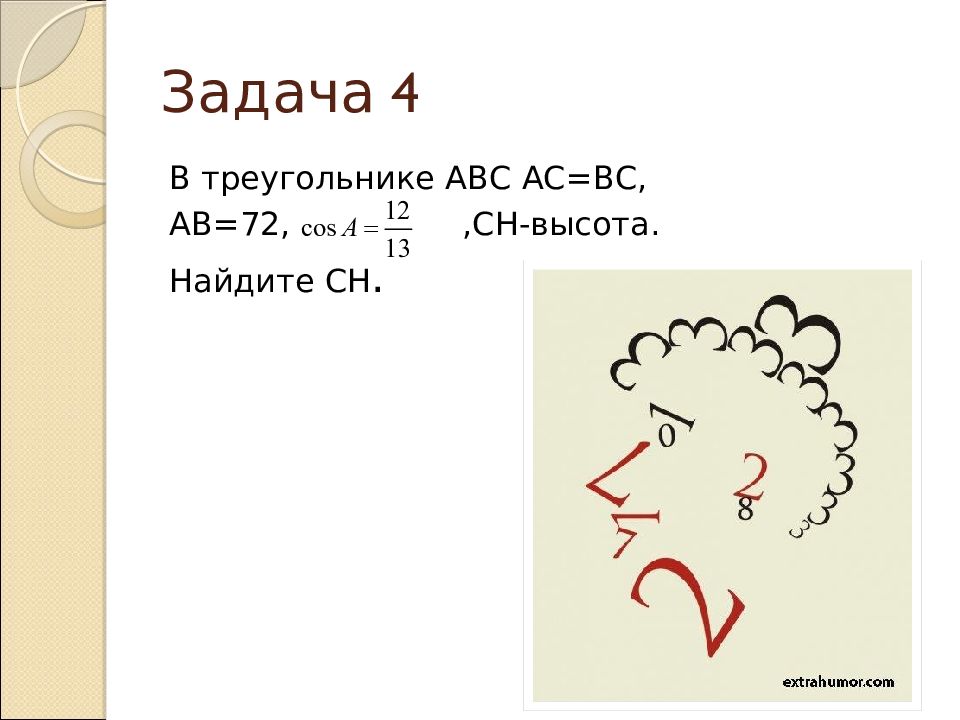
Слайд 19: Задача 8
В треугольнике АВС угол С равен 90, , ВС=7. Найдите тангенс внешнего угла при вершине А.
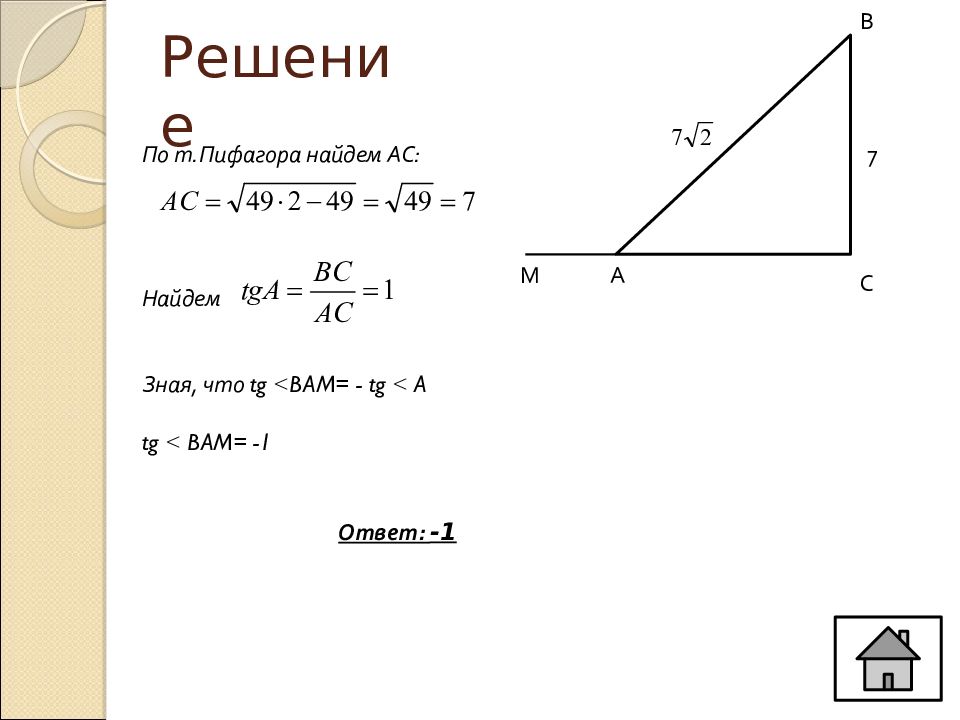
Слайд 20: Решение
С В А 7 М По т.Пифагора найдем АС: Найдем Зная, что tg ˂ BAM= - tg ˂ A tg ˂ BAM= -1 Ответ: -1
Слайд 21: Задания повышенного уровня
ЧТО НЕОБХОДИМО ЗНАТЬ ДЛЯ РЕШЕНИЯ: Сумма противолежащих углов четырехугольника, вписанного в окружность, равна 180 0. Сумма углов треугольника равна 180 0. Углы, опирающиеся на одну и ту же хорду, равны.
Слайд 22: Задача 9*
Четырехугольник ABCD вписан в окружность. Угол АВС равен 105, угол СА D равен 35. Найдите угол АВ D, ответ дайте в градусах.
Последний слайд презентации: Решение заданий типа №15, №16 ОГЭ: Решение
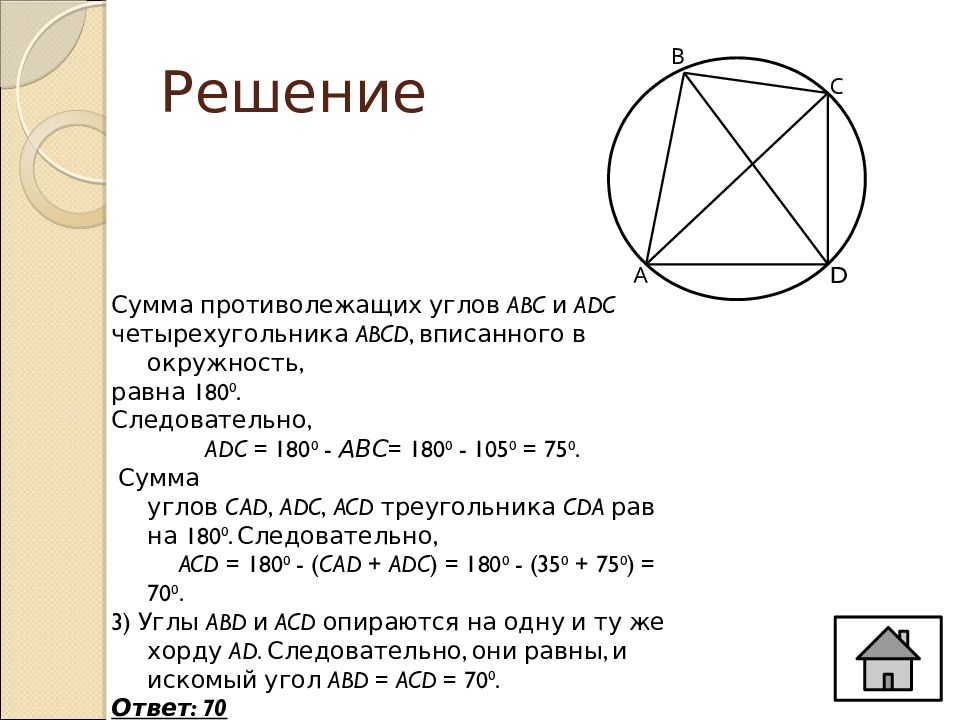
В С А D Сумма противолежащих углов ABC и ADC четырехугольника ABCD, вписанного в окружность, равна 180 0. Следовательно, A DC = 180 0 - АВС = 180 0 - 105 0 = 75 0. Сумма углов CAD, ADC, ACD треугольника CDA равна 180 0. Следовательно, ACD = 180 0 - ( CAD + ADC ) = 180 0 - (35 0 + 75 0 ) = 70 0. 3) Углы ABD и ACD опираются на одну и ту же хорду AD. Следовательно, они равны, и искомый угол ABD = ACD = 70 0. Ответ: 70