Решение заданий 14 (С2) по материалам ЕГЭ профильного уровня нахождение углов, расстояний, построение сечений
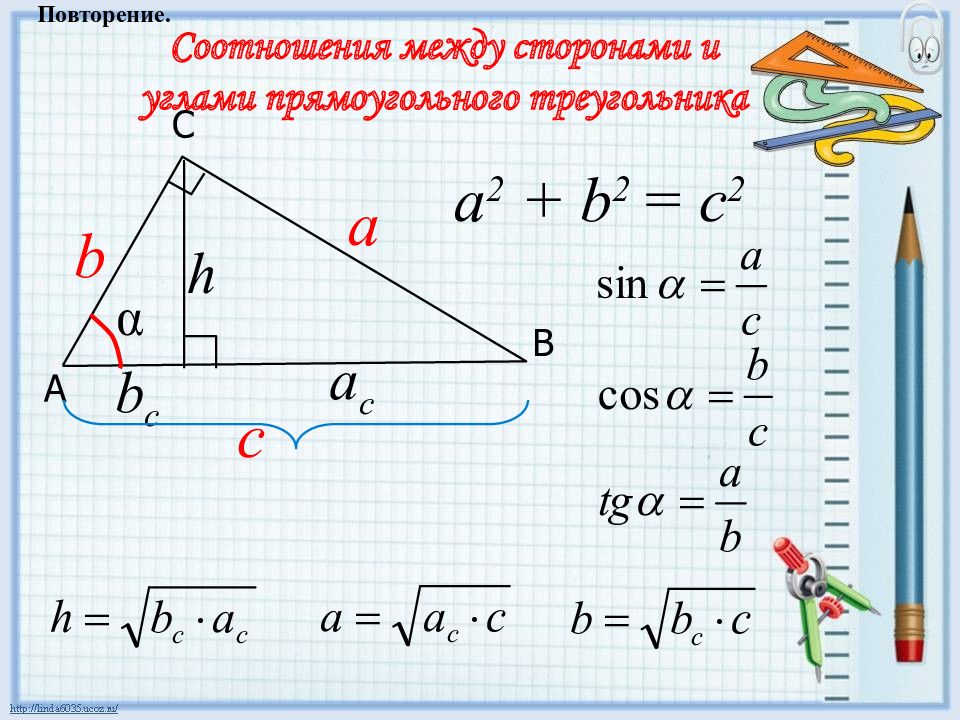
Соотношения между сторонами и углами прямоугольного треугольника Повторение. C A В a 2 + b 2 = c 2 c b a b c a c h α
a 2 = B a A C c b Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними. Квадрат стороны треугольника равен сумме квадратов двух других сторон на косинус угла между ними. минус удвоенное произведение этих сторон b 2 + c 2 – 2bc cosA Теорема косинусов
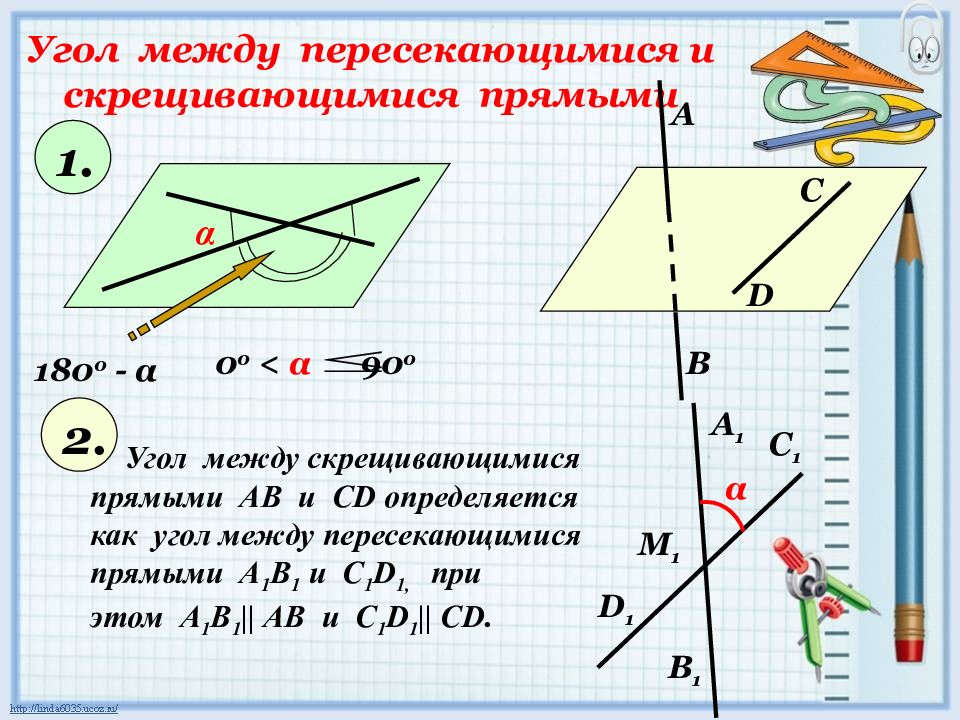
Угол между пересекающимися и скрещивающимися прямыми α 180 0 - α 0 0 < α 90 0 1. 2. Угол между скрещивающимися прямыми АВ и С D определяется как угол между пересекающимися прямыми А 1 В 1 и С 1 D 1, при этом А 1 В 1 || АВ и С 1 D 1 || CD. А В D С А 1 В 1 С 1 D 1 α М 1
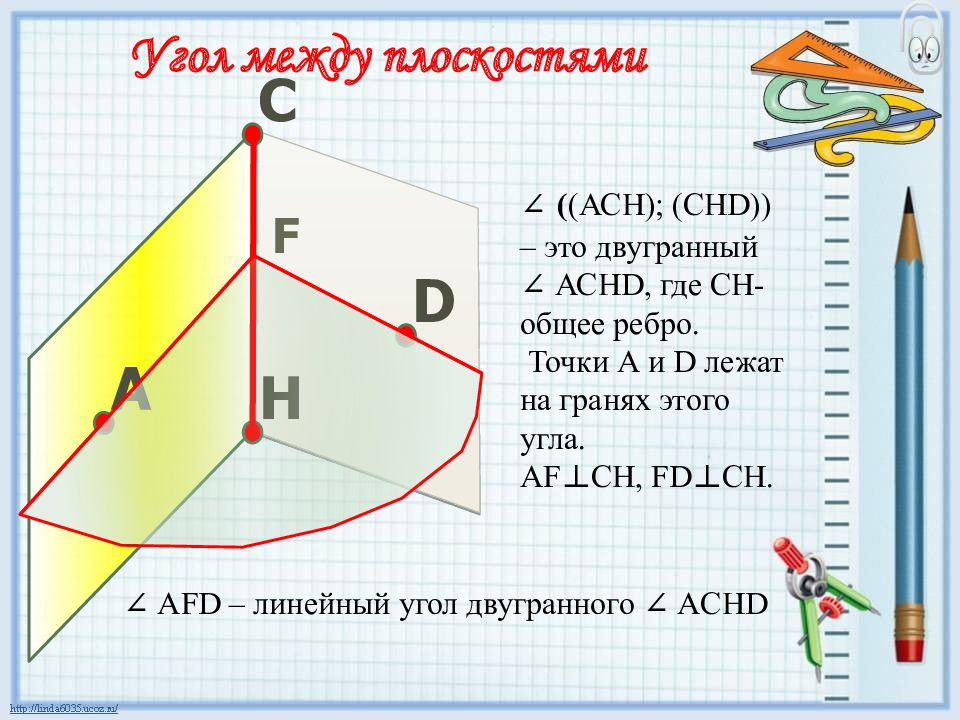
A D C H ∠ ( (АСН); (СН D )) – это двугранный ∠ АСН D, где СН-общее ребро. Точки А и D лежат на гранях этого угла. AF⊥CH, FD⊥CH. F ∠ AFD – линейный угол двугранного ∠ А CHD Угол между плоскостями
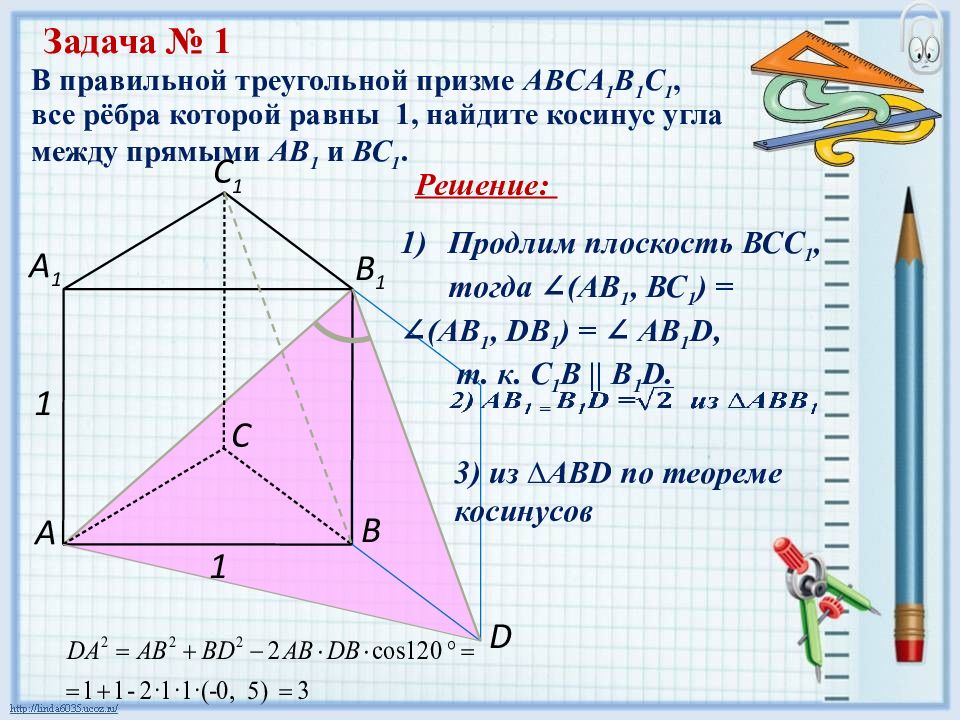
В правильной треугольной призме ABCA 1 B 1 C 1, все рёбра которой равны 1, найдите косинус угла между прямыми АВ 1 и ВС 1. Задача № 1 1 А С В D А 1 С 1 В 1 1 3) из ∆ABD по теореме косинусов Продлим плоскость ВСС 1, тогда ∠(AB 1, ВС 1 ) = ∠(AB 1, DВ 1 ) = ∠ AВ 1 D, т. к. C 1 В || B 1 D. Решение:
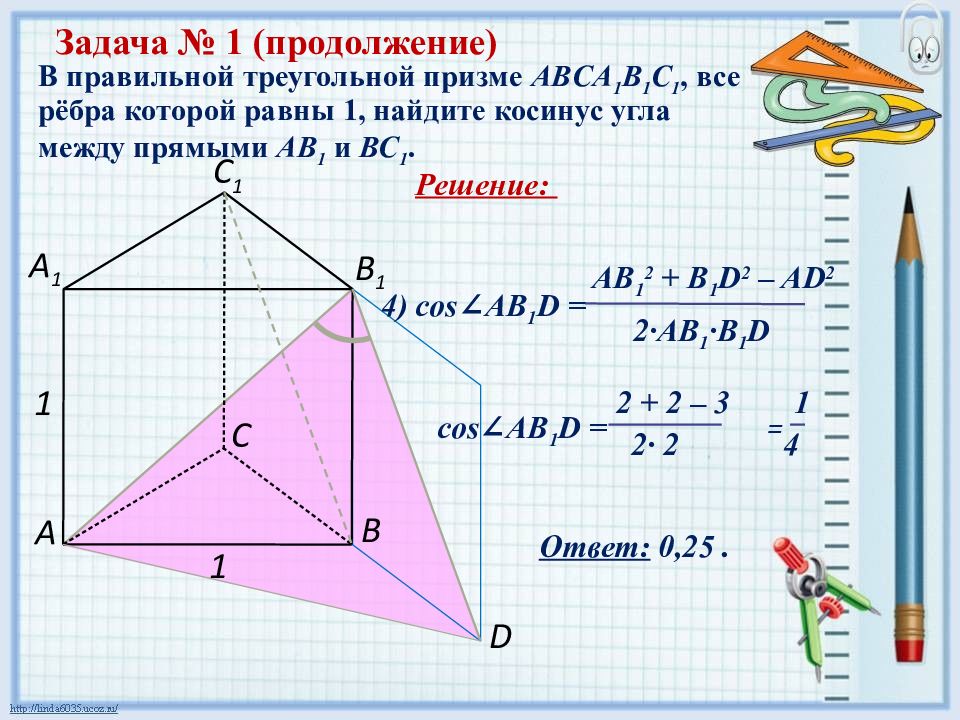
В правильной треугольной призме ABCA 1 B 1 C 1, все рёбра которой равны 1, найдите косинус угла между прямыми АВ 1 и ВС 1. Задача № 1 (продолжение) 1 А С В D А 1 С 1 В 1 1 Решение: 4) cos ∠ AB 1 D = AB 1 2 + B 1 D 2 – AD 2 2·AB 1 · B 1 D cos ∠ AB 1 D = = 2 + 2 – 3 1 2· 2 4 Ответ: 0,25.
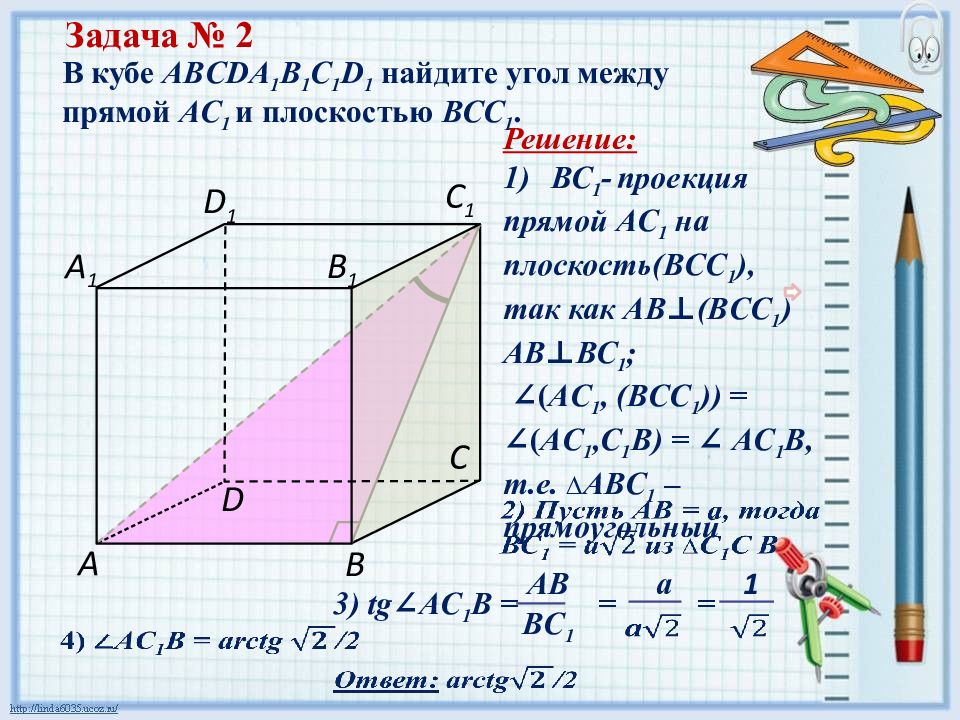
В кубе ABCDA 1 B 1 C 1 D 1 найдите угол между прямой AC 1 и плоскостью ВС C 1. Задача № 2 С В D А 1 С 1 В 1 D 1 А Решение: ВС 1 - проекция прямой АС 1 на плоскость(В C С 1 ), так как AB ⊥ (В C С 1 ) AB ⊥ ВС 1 ; ∠( AC 1, ( В C С 1 ) ) = ∠( A С 1,С 1 В) = ∠ AC 1 B, т.е. ∆ АВC 1 – прямоугольный 3) tg ∠ AC 1 B = = = AB a 1 BC 1
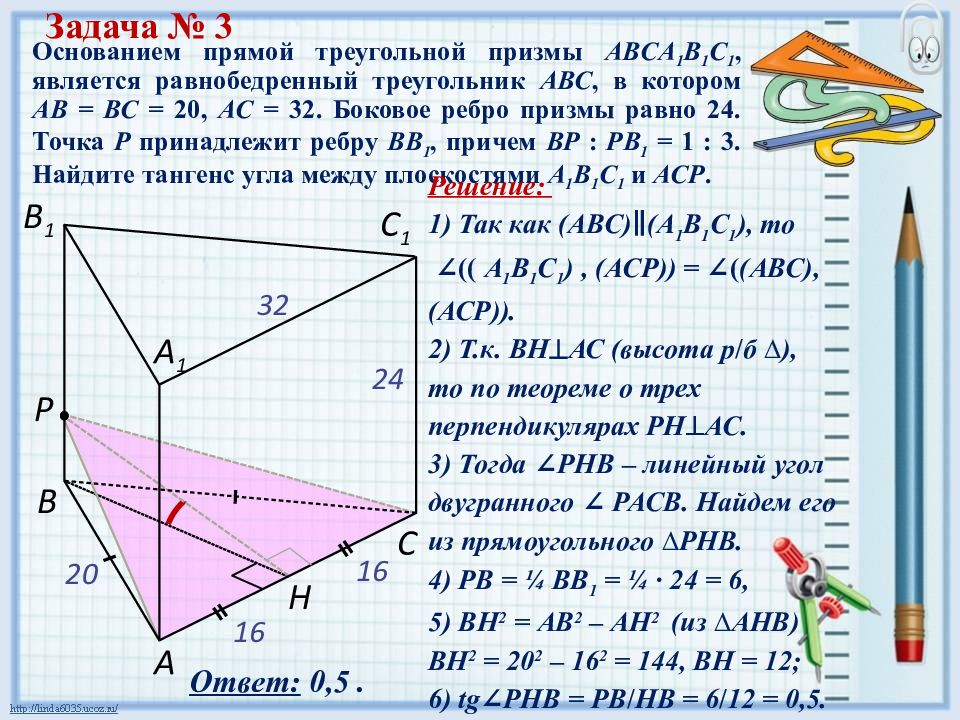
Основанием прямой треугольной призмы ABCA 1 B 1 C 1, является равнобедренный треугольник АВС, в котором АВ = ВС = 20, АС = 32. Боковое ребро призмы равно 24. Точка Р принадлежит ребру ВВ 1, причем ВР : РВ 1 = 1 : 3. Найдите тангенс угла между плоскостями А 1 В 1 С 1 и АСР. 20 А С В А 1 С 1 В 1 24 Ответ: 0,5. Задача № 3 Р Н 16 16 Решение: 1) Так как (АВС) ∥ (А 1 В 1 С 1 ), то ∠(( А 1 В 1 С 1 ), (АСР)) = ∠( (АВС),(АСР)). 2) Т.к. ВН АС (высота р / б ∆ ), то по теореме о трех перпендикулярах РН АС. 3) Тогда ∠ РНВ – линейный угол двугранного ∠ РАСВ. Найдем его из прямоугольного ∆ РНВ. 4) РВ = ¼ ВВ 1 = ¼ · 24 = 6, 5) ВН 2 = АВ 2 – АН 2 (из ∆ A НВ) ВН 2 = 20 2 – 16 2 = 144, ВН = 12; 6) tg ∠ РНВ = PB / HB = 6 / 12 = 0,5. 32
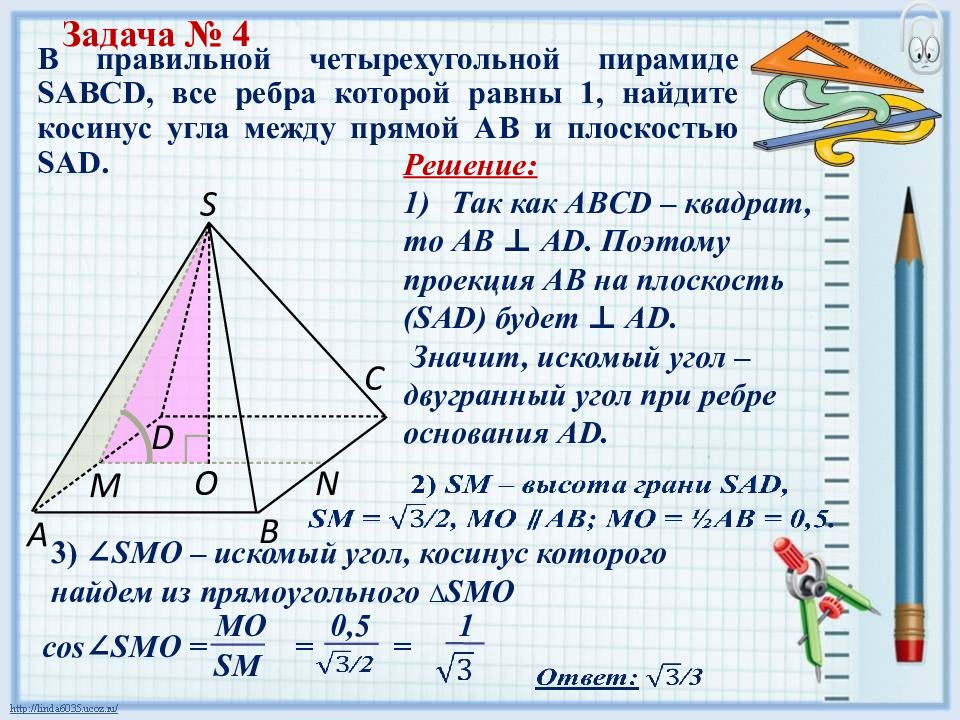
Решение: Так как ABCD – квадрат, то АВ ⊥ AD. Поэтому проекция AB на плоскость (SAD) будет ⊥ AD. Значит, искомый угол – двугранный угол при ребре основания AD. В правильной четырехугольной пирамиде S ABCD, все ребра которой равны 1, найдите косинус угла между прямой AB и плоскостью SAD. Задача № 4 С В D А S O M N 3) ∠ SMO – искомый угол, косинус которого найдем из прямоугольного ∆ SMO cos ∠ SMO = = = MO 0,5 1 SM
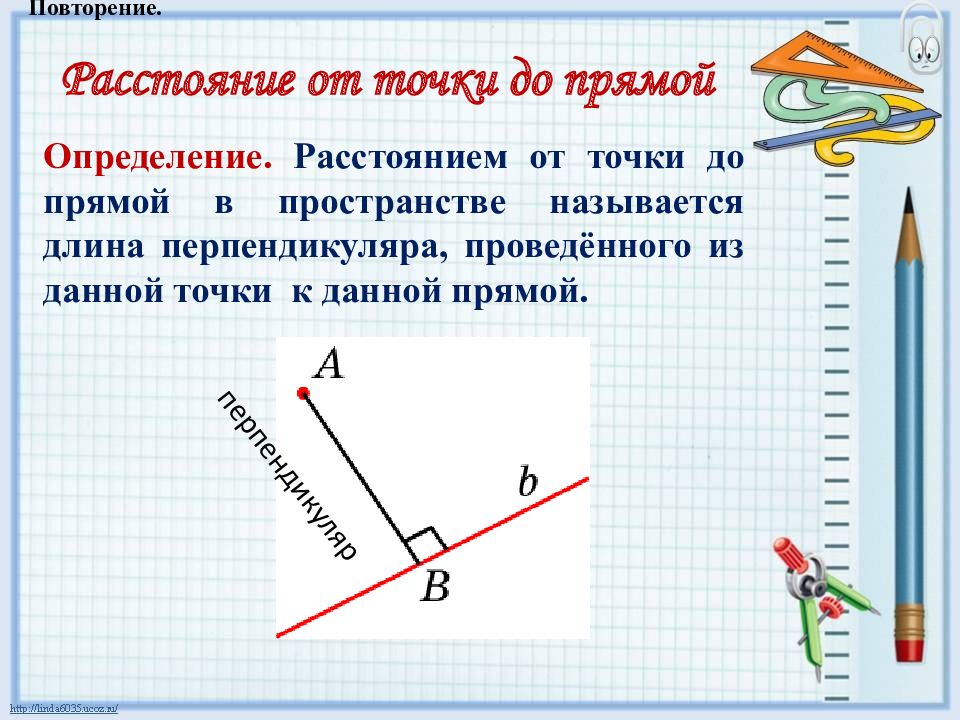
Расстояние от точки до прямой Определение. Расстоянием от точки до прямой в пространстве называется длина перпендикуляра, проведённого из данной точки к данной прямой. перпендикуляр Повторение.
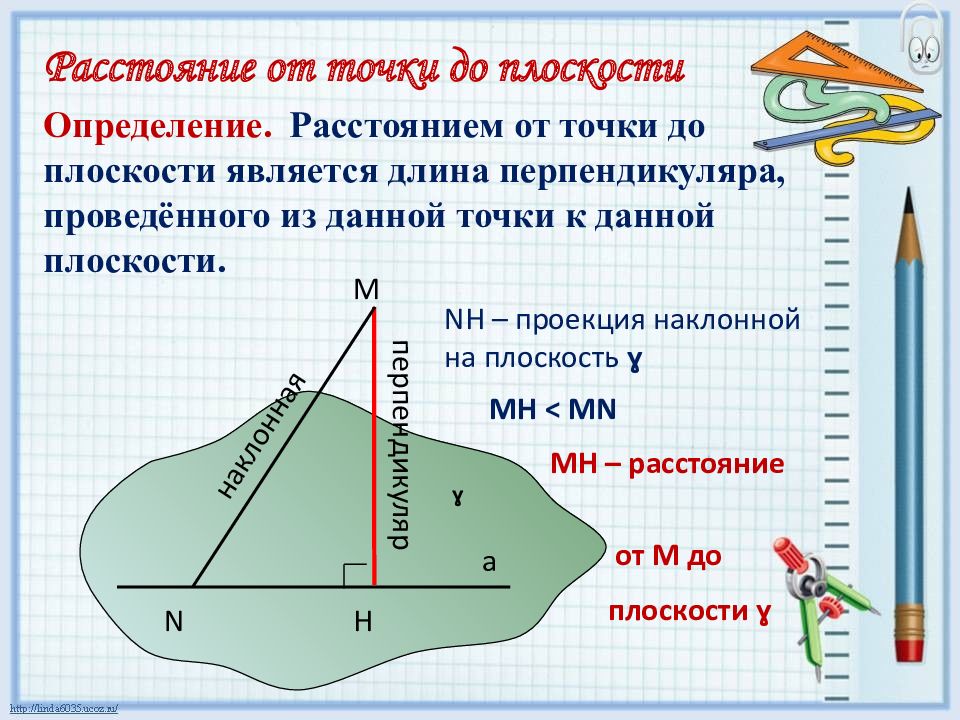
Расстояние от точки до плоскости Определение. Расстоянием от точки до плоскости является длина перпендикуляра, проведённого из данной точки к данной плоскости. перпендикуляр a ɣ M H N наклонная NH – проекция наклонной на плоскость ɣ MH < MN М H – расстояние от М до плоскости ɣ
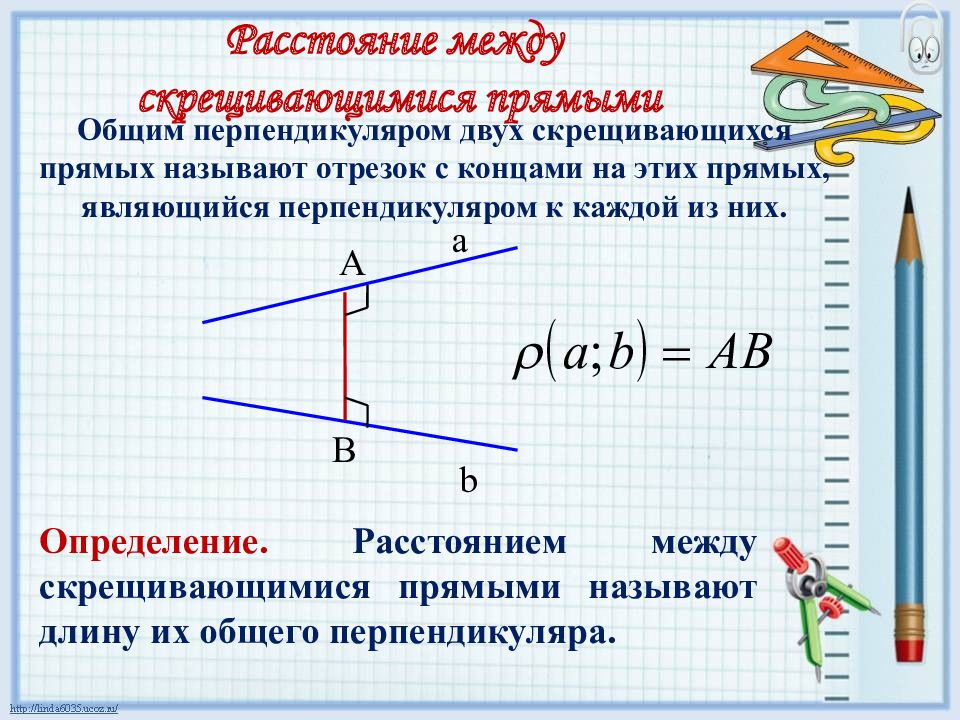
Общим перпендикуляром двух скрещивающихся прямых называют отрезок с концами на этих прямых, являющийся перпендикуляром к каждой из них. a b A B Определение. Расстоянием между скрещивающимися прямыми называют длину их общего перпендикуляра. Расстояние между скрещивающимися прямыми
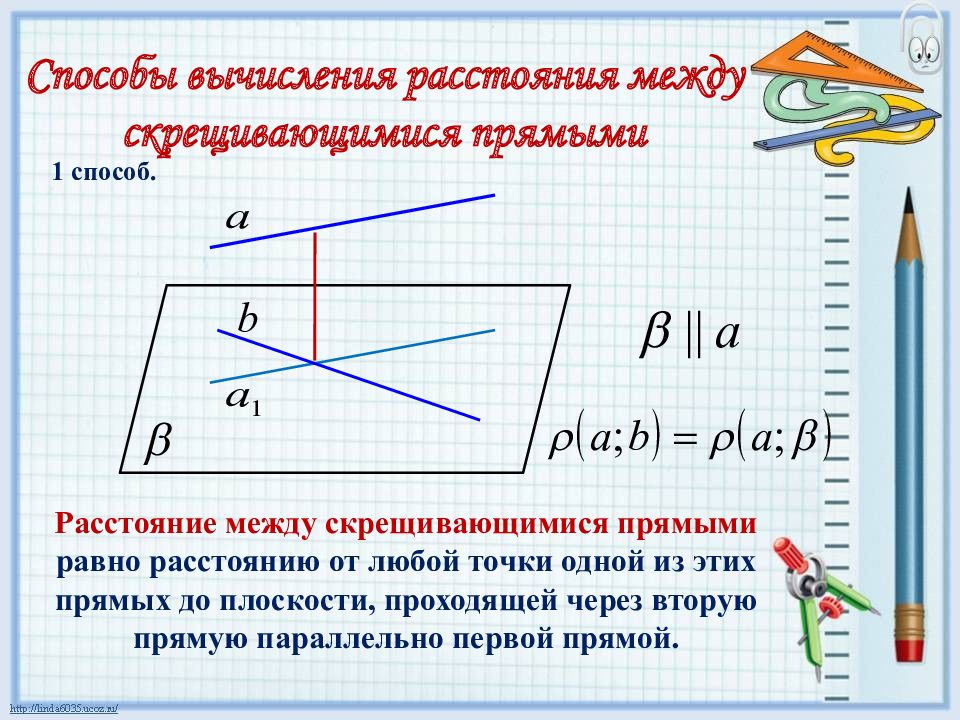
Способы вычисления расстояния между скрещивающимися прямыми Расстояние между скрещивающимися прямыми равно расстоянию от любой точки одной из этих прямых до плоскости, проходящей через вторую прямую параллельно первой прямой. 1 способ.
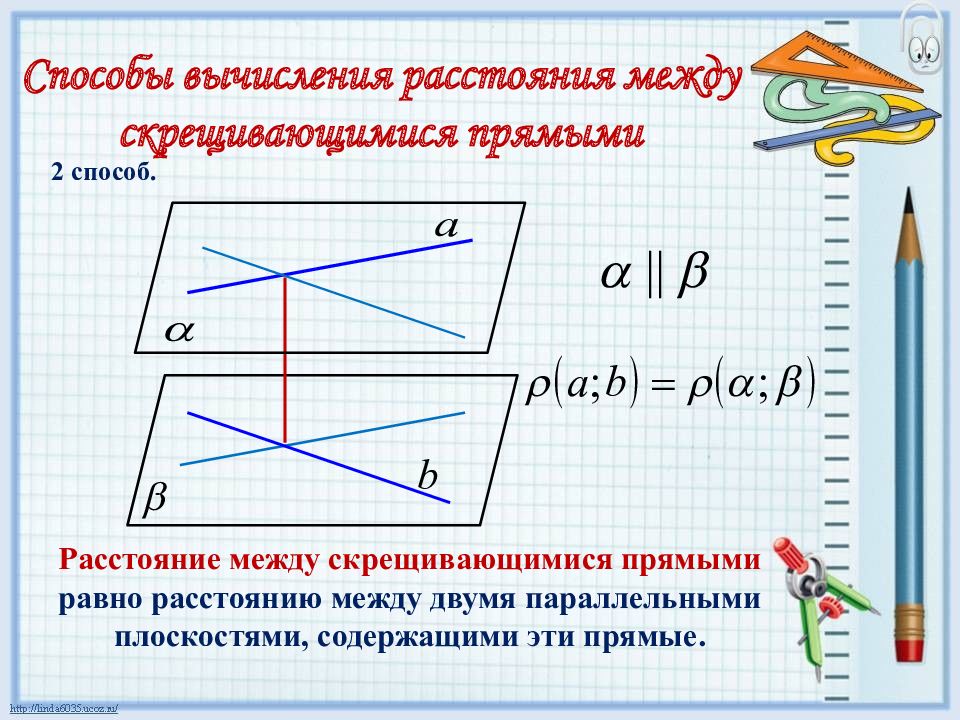
Способы вычисления расстояния между скрещивающимися прямыми Расстояние между скрещивающимися прямыми равно расстоянию между двумя параллельными плоскостями, содержащими эти прямые. 2 способ.
Способы вычисления расстояния между скрещивающимися прямыми Расстояние между скрещивающимися прямыми равно расстоянию между их проекциями на плоскость, перпендикулярную одной из них. 3 способ.
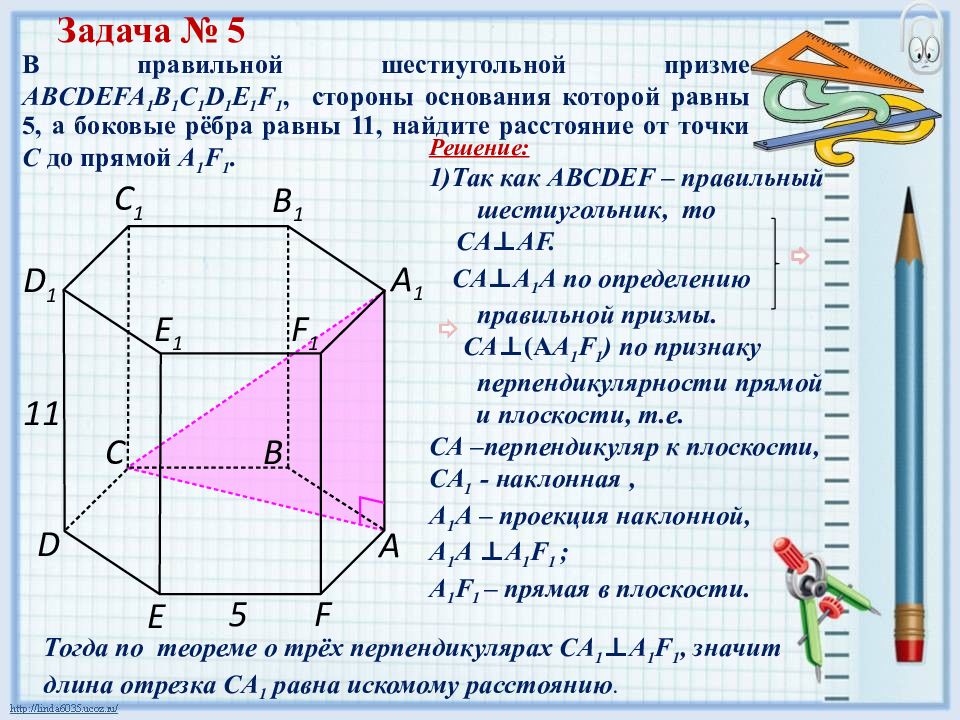
В правильной шестиугольной призме ABCDEFA 1 B 1 C 1 D 1 E 1 F 1, стороны основания которой равны 5, а боковые рёбра равны 11, найдите расстояние от точки С до прямой A 1 F 1. Задача № 5 Решение: 1)Так как ABCDEF – правильный шестиугольник, то C A ⊥ AF. C A ⊥ A 1 А по определению правильной призмы. C A ⊥(А A 1 F 1 ) по признаку перпендикулярности прямой и плоскости, т.е. СА –перпендикуляр к плоскости, C A 1 - наклонная, A 1 А – проекция наклонной, A 1 А ⊥ A 1 F 1 ; A 1 F 1 – прямая в плоскости. 5 А С В D F E А 1 С 1 В 1 D 1 F 1 E 1 11 Тогда по теореме о трёх перпендикулярах CA 1 ⊥ A 1 F 1, значит длина отрезка C A 1 равна искомому расстоянию.
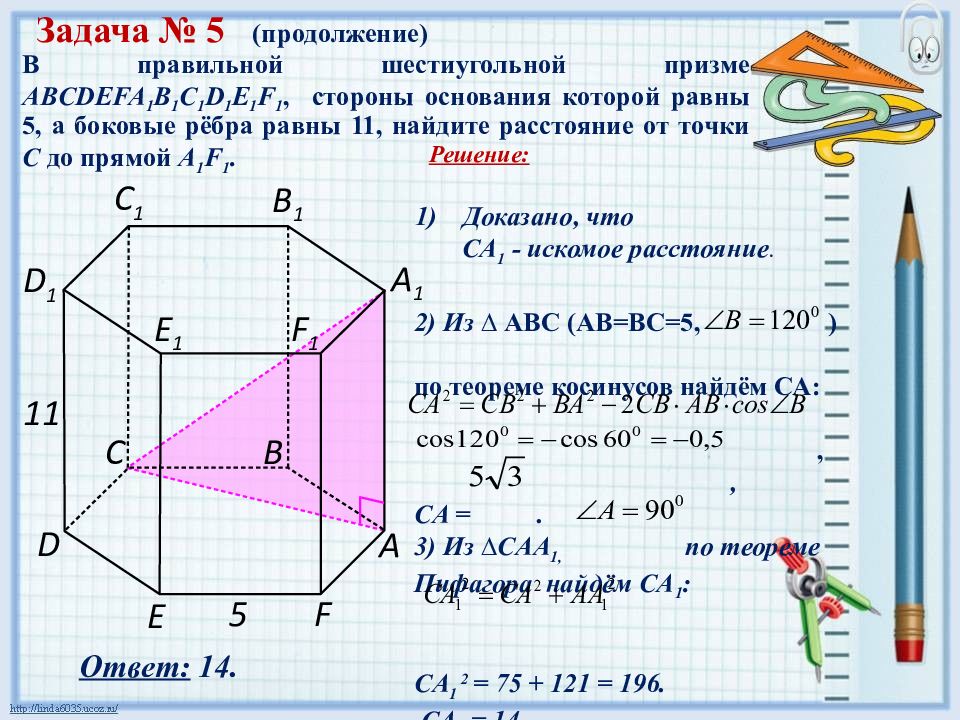
В правильной шестиугольной призме ABCDEFA 1 B 1 C 1 D 1 E 1 F 1, стороны основания которой равны 5, а боковые рёбра равны 11, найдите расстояние от точки С до прямой A 1 F 1. Задача № 5 (продолжение) Решение: 2) Из ∆ АВС (АВ=ВС=5, ) по теореме косинусов найдём СА: , , C A =. 3) Из ∆ CAA 1, по теореме Пифагора найдём CA 1 : CA 1 2 = 75 + 121 = 196. CA 1 = 14 Ответ: 14. 5 А С В D F E А 1 С 1 В 1 D 1 F 1 E 1 11 Доказано, что C A 1 - искомое расстояние.
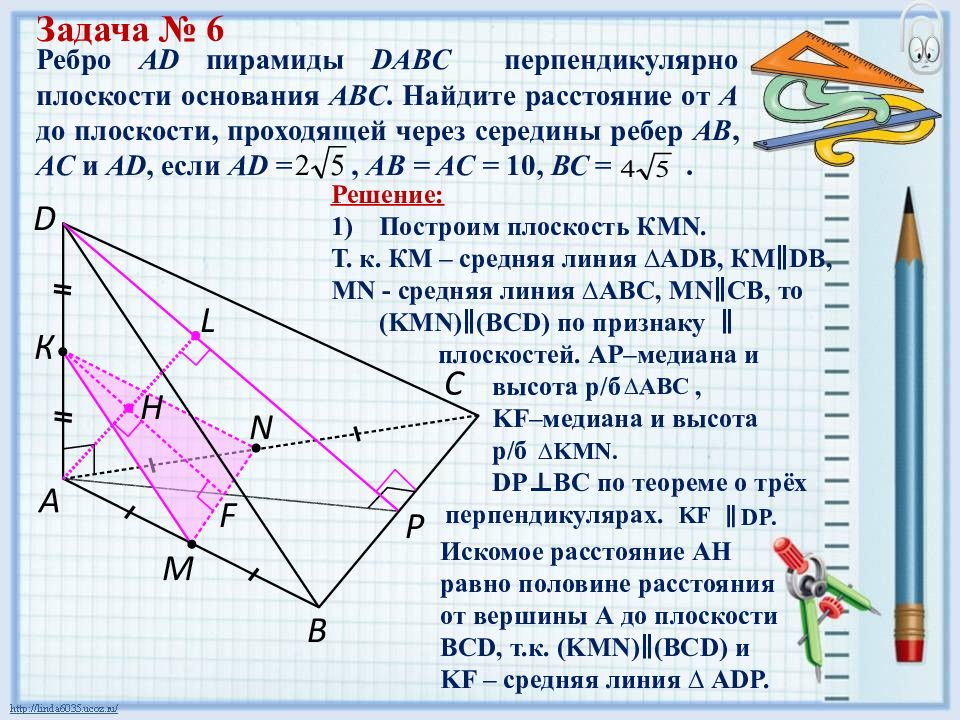
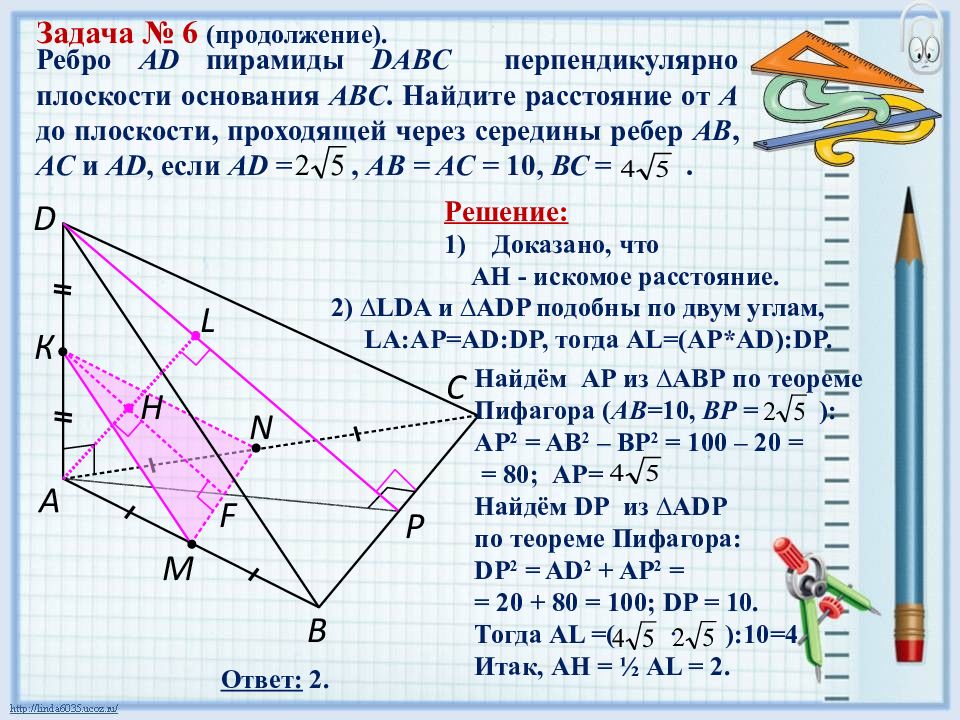
Ребро AD пирамиды DABC перпендикулярно плоскости основания АВС. Найдите расстояние от А до плоскости, проходящей через середины ребер АВ, АС и А D, если А D =, АВ = АС = 10, ВС =. D C B A N F М К Р Искомое расстояние AH равно половине расстояния от вершины А до плоскости BCD, т.к. (KMN) ∥ (BCD) и KF – средняя линия ∆ ADP. L Н Задача № 6 Решение: Построим плоскость КМ N. Т. к. КМ – средняя линия ∆А D В, КМ∥ D В, MN - средняя линия ∆АВ C, М N ∥ C В, то (KMN) ∥ (BCD) по признаку ∥ плоскостей. АР–медиана и высота р/б, KF –медиана и высота р/б DP ⊥ BC по теореме о трёх перпендикулярах. ∆АВ C ∆ KMN. KF ∥ DP.
Ребро AD пирамиды DABC перпендикулярно плоскости основания АВС. Найдите расстояние от А до плоскости, проходящей через середины ребер АВ, АС и А D, если А D =, АВ = АС = 10, ВС =. D C B A N F М К Р Решение: Доказано, что AH - искомое расстояние. Найдём АР из ∆АВР по теореме Пифагора ( АВ= 10, ВР = ): AP 2 = AB 2 – BP 2 = 100 – 20 = = 80 ; АР= Найдём D Р из ∆А D Р по теореме Пифагора: DP 2 = AD 2 + AP 2 = = 20 + 80 = 100 ; DP = 10. Тогда AL =( · ) : 10=4 Итак, АН = ½ AL = 2. L Н Ответ: 2. Задача № 6 (продолжение). 2) ∆ LDA и ∆ ADP подобны по двум углам, LA:AP=AD:DP, тогда AL=(AP*AD):DP.
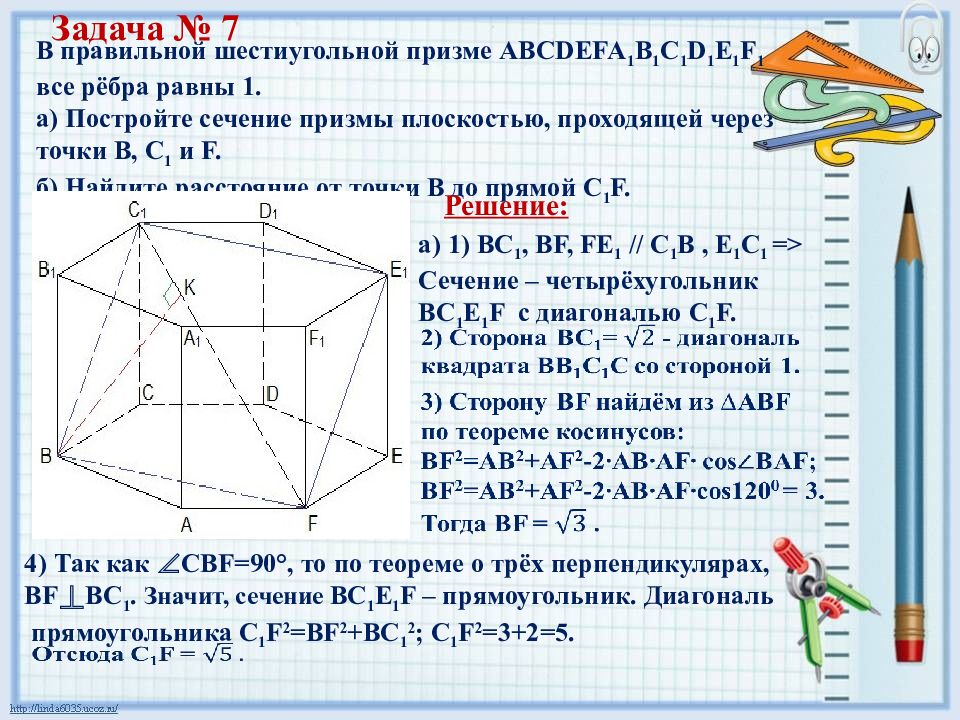
Задача № 7 В правильной шестиугольной призме АВCDEFA 1 B 1 C 1 D 1 E 1 F 1 все рёбра равны 1. а) Постройте сечение призмы плоскостью, проходящей через точки B, С 1 и F. б) Найдите расстояние от точки В до прямой C 1 F. Решение: а) 1) ВС 1, BF, F Е 1 // С 1 B, Е 1 C 1 => Сечение – четырёхугольник BC 1 E 1 F с диагональю C 1 F. 4) Так как ∠ CBF=90°, то по теореме о трёх перпендикулярах, BF ⟘ BC 1. Значит, сечение BC 1 E 1 F – прямоугольник. Диагональ прямоугольника C 1 F 2 =BF 2 +BC 1 2 ; C 1 F 2 =3+2=5.
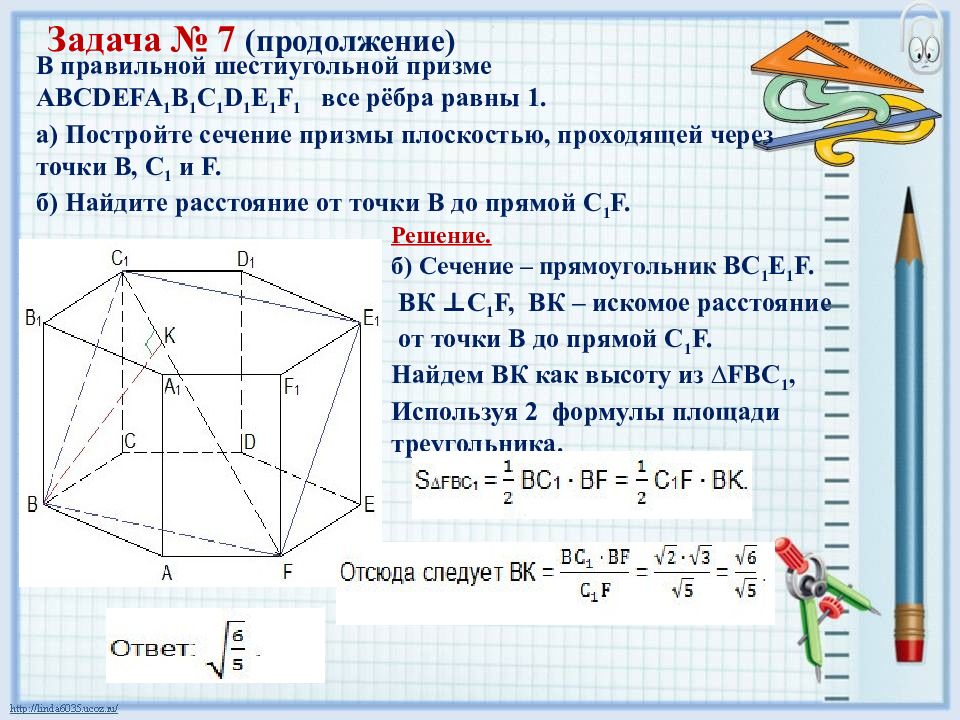
Задача № 7 (продолжение) Решение. б) Сечение – прямоугольник BC 1 E 1 F. ВК ⊥C 1 F, ВК – искомое расстояние от точки В до прямой C 1 F. Найдем ВК как высоту из ∆FBС 1, Используя 2 формулы площади треугольника. В правильной шестиугольной призме АВCDEFA 1 B 1 C 1 D 1 E 1 F 1 все рёбра равны 1. а) Постройте сечение призмы плоскостью, проходящей через точки B, С 1 и F. б) Найдите расстояние от точки В до прямой C 1 F.
Задача №8 Основанием прямой четырехугольной призмы является квадрат ABCD со стороной, высота призмы равна . Точка K − середина ребра ВВ1. Через точки K и С1 проведена плоскость α, параллельная прямой BD1. а) Докажите, что сечение призмы плоскостью α является равнобедренным треугольником. б) Найдите периметр треугольника, являющегося сечением призмы плоскостью α. Решение. а) Для построения сечения призмы плоскостью α, проведём КЕ|| BD 1, E € B 1 D 1. Плоскость α проходит через точки К, С 1 и Е. Так как К – середина ВВ 1 и КЕ|| BD 1, то Е – середина диагонали А 1 С 1 квадрата А 1 В 1 С 1 D 1. Значит, плоскость α пересекает грань А 1 В 1 С 1 D 1 по диагонали А 1 С 1. Соединив точки К, С 1 и А 1, получаем ∆А 1 КС 1 - сечение призмы плоскостью α. ∆А 1 КВ 1 = ∆С 1 КВ 1 по двум сторонам и углу между ними (А 1 В 1 =С 1 В 1 ), В 1 К – общая сторона,. Из равенства треугольников следует, что А 1 К=С 1 К, значит ∆А 1 КС 1 - равнобедренный.
Задача №8 (продолжение) Основанием прямой четырехугольной призмы ABCDA 1 B 1 C 1 D 1 является квадрат ABCD со стороной, высота призмы равна . Точка K − середина ребра ВВ 1. Через точки K и С 1 проведена плоскость α, параллельная прямой BD 1. а) Докажите, что сечение призмы плоскостью α является равнобедренным треугольником. б) Найдите периметр треугольника, являющегося сечением призмы плоскостью α. Решение. б)
Задачи для самостоятельного решения На ребре AA1 прямоугольного параллелепипеда ABCDA 1 B 1 C 1 D 1 взята точка E так, что A 1 E : EA = 2:5, на ребре BB 1 — точка F так, что B 1 F : FB =1: 6, а точка Т — середина ребра B 1 C 1. Известно, что AB = 5, AD = 6, AA 1 =14. а) Докажите, что плоскость EFT проходит через вершину D 1. б) Найдите угол между плоскостью EFT и плоскостью AA 1 B 1. 2) Дана правильная треугольная призма ABCA 1 B 1 C 1, все рёбра которой равны 4. Через точки A, С 1 и середину T ребра А 1 В 1 проведена плоскость. а) Докажите, что сечение призмы указанной плоскостью является прямоугольным треугольником. б) Найдите угол между плоскостью сечения и плоскостью ABC. Ответ: б) arctg 2.
Задачи для самостоятельного решения 3) В правильной шестиугольной призме А…F 1 все рёбра равны 2. а) Докажите, что плоскость ВВ 1 F перпендикулярна прямой В 1 С 1. б) Найдите расстояние от точки В до плоскости F В 1 С 1. 4) В пирамиде D АВС известны длины ребер АВ=АС= D В= D С=13, D А =6, ВС=24. а) Постройте прямую, перпендикулярную прямым DА и ВС. б) Найдите расстояние между прямыми DА и ВС. Ответ: б) 4.
Задачи для самостоятельного решения 5 ) Высота правильной треугольной пирамиды равна 20, а медиана её основания равна 6. а) Постройте сечение пирамиды плоскостью, проходящей через её вершину и перпендикулярной ребру основания. б) Найдите тангенс угла, который образует боковое ребро с плоскостью основания. 6) В правильной четырёхугольной пирамиде МАВСD с вершиной М сторона основания равна 3, а боковое ребро равно 6. а) Постройте сечение пирамиды плоскостью, проходящей через точку С и середину ребра МА параллельно прямой ВD. б) Найдите площадь этого сечения. Ответ: б) 5. Ответ: б) 6.
Используемая литература: 1) И. В. Ященко, С.А. Шестаков, А. С. Трепалин «Подготовка к ЕГЭ по математике 2016, профильный уровень», Москва, издательство МЦНМО, 2016. 2) Интернет-ресурсы: http://www.fipi.ru/ http://mathege.ru/or/ege/Main https://math-ege.sdamgia.ru/ http://alexlarin.net/ https://ege-ok.ru/ 3) Шаблон презентации сайт http://pedsovet.su/, автор Фокина Л. П.
