Системы счисления: от пальцев до кода Kimi AI 2025/01/01
01 Введение и унарная система 02 Непозиционные системы 03 Позиционные системы 04 Двоичная и родственные системы 05 Перевод и задачи 06 Итог и выводы CONTENTS
01 Введение и унарная система
Определение системы счисления Система счисления — это набор правил для записи чисел с помощью цифр и выполнения арифметических операций. Она позволяет преобразовать любую информацию в числовую форму, понятную компьютеру. 01 Роль двоичного кода Все данные в компьютере хранятся в виде двоичных чисел. Процессор оперирует только нулями и единицами, что делает двоичную систему счисления основным языком машин. 02 Цель изучения Узнав, как числа записываются в разных системах счисления, мы поймём, почему двоичная система так важна и как любые данные можно представить в виде двоичного кода. 03 Зачем компьютеру системы счисления
Особенности унарной системы Унарная система — самая простая. Каждый знак означает единицу, и числа записываются повторением этого знака. Например, 3 — это три черточки или три камешка. Недостатки унарной системы Унарная система подходит только для натуральных чисел. Запись больших чисел становится громоздкой, например, миллион потребует миллиона повторений знака. Унарная система: счёт без алфавита
02 Непозиционные системы
Символы египетской системы Египетская система использует семь иероглифов для степеней десяти: черта (1), хомут (10), верёвка (100), лотос (1000), палец (10 000), лягушка (100 000) и человек (1 000 000). Недостатки египетской системы Для записи больших чисел требуется множество иероглифов, что делает систему громоздкой. Арифметические операции также становятся сложными из-за большого количества символов. Значение иероглифов Каждый иероглиф всегда означает ту же величину, независимо от места в записи числа. Например, число 123 записывается как один лотос, два хомута и три черточки. Пример числа Например, число 2468 в египетской системе будет записано как два лотоса, четыре хомута, шесть верёвок и восемь черточек. Египетские иероглифы: семь значков
Символы римской системы Римская система использует латинские буквы: I (1), V (5), X (10), L (50), C (100), D (500) и M (1000). Правило вычитания Меньшая цифра перед большей вычитается. Например, IV означает 4 (5 - 1), а IX означает 9 (10 - 1). Недостатки римской системы Римская система ограничена натуральными числами, для больших чисел нужны новые символы. Арифметические операции сложны из-за множества правил. Римские цифры: вычитание справа
02 01 Символы славянской системы Славянская система использует буквы алфавита с титлом. Например, А (1), В (2), Г (3) и так далее. Титло ставится над предпоследней цифрой. Пример числа Число 11 записывается как А с титлом и Г без титла. Славянская система была использована в старинных рукописях и на некоторых часах. Славянская система: буквы с титлом
03 Позиционные системы
Определение позиционной системы В позиционной системе значение цифры зависит от её места в числе. Например, в числе 6375 цифра 6 означает 6 тысяч, а цифра 5 — 5 единиц. 01 Разряды в десятичной системе Разряды нумеруются справа налево с нуля. В числе 6375: 5 в нулевом разряде (единицы), 7 в первом (десятки), 3 во втором (сотни), 6 в третьем (тысячи). 02 Преимущества позиционной системы Позиционная система позволяет компактно записывать числа и легко выполнять арифметические операции. Это делает её идеальной для вычислений. 03 Развёрнутая форма числа Число 6375 можно записать в развёрнутой форме: 6·10³ + 3·10² + 7·10¹ + 5·10⁰. Это помогает понять, как значение цифры зависит от её разряда. 04 Десятичная система: вес цифры в разряде
Алфавит, основание и разряд Алфавит системы счисления Алфавит — это набор цифр, используемых в системе. Например, в десятичной системе алфавит состоит из цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Основание системы счисления Основание системы счисления — это количество цифр в алфавите. В десятичной системе основание равно 10, в двоичной — 2. Значение разряда Разряд — это позиция цифры в числе. Например, в числе 6375 цифра 6 находится в третьем разряде, что означает 6 тысяч.
04 Двоичная и родственные системы
Особенности двоичной системы Двоичная система имеет основание 2 и алфавит 0 и 1. Любое число записывается как сумма степеней двойки. Например, число 1011₂ означает 1·2³ + 0·2² + 1·2¹ + 1·2⁰ = 11. Преимущества двоичной системы Двоичная система идеально подходит для компьютеров,因为她使用简单的0和1表示，这与电子元件的两种状态（开和关）相对应，使得存储和处理数据变得非常高效。 Двоичная система: язык процессора
Шестнадцатеричная система Шестнадцатеричная система имеет основание 16 и алфавит 0-9 и A-F. Она также используется для компактной записи двоичных чисел. Например, двоичное число 101101₂ записывается как 2D₁₆. 01 Восьмеричная система Восьмеричная система имеет основание 8 и алфавит 0-7. Она используется для компактной записи двоичных чисел. Например, двоичное число 101101₂ записывается как 55₈. Преимущества сжатия кода Восьмеричная и шестнадцатеричная системы позволяют сократить запись двоичных чисел в 3 или 4 раза, что облегчает чтение и запись машинных кодов, адресов памяти и цветовых кодов в веб-страницах. 02 Восьмеричная и шестнадцатеричная: сжатие кода
05 Перевод и задачи
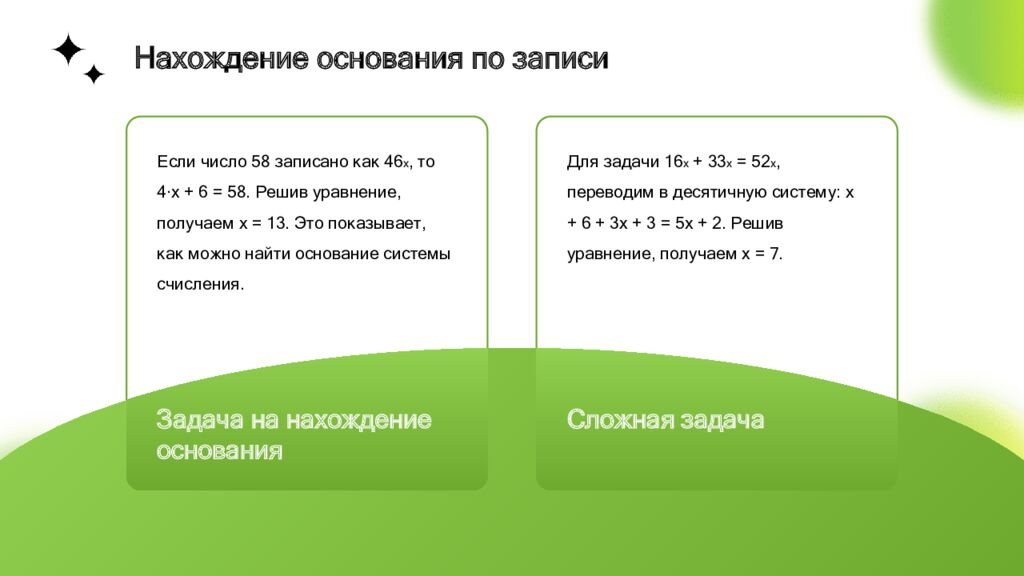
Развёрнутая форма числа Любое позиционное число можно записать в развёрнутой форме. Например, число 325ₓ можно записать как 3·x² + 2·x + 5. Это позволяет перевести число в десятичную систему. Пример перевода Если число 46ₓ равно 58 в десятичной системе, то 4·x + 6 = 58. Решив это уравнение, получаем x = 13. Значение развёрнутой формы Развёрнутая форма помогает понять, как значение цифры зависит от её разряда и основания системы счисления. Это ключ к переводу между системами. Развёрнутая форма: универсальный ключ
Для задачи 16ₓ + 33ₓ = 52ₓ, переводим в десятичную систему: x + 6 + 3x + 3 = 5x + 2. Решив уравнение, получаем x = 7. Сложная задача Если число 58 записано как 46ₓ, то 4·x + 6 = 58. Решив уравнение, получаем x = 13. Это показывает, как можно найти основание системы счисления. Задача на нахождение основания Нахождение основания по записи
06 Итог и выводы
Системы счисления Система счисления — это набор правил для записи чисел и выполнения операций. Она может быть непозиционной или позиционной, в зависимости от того, зависит ли значение цифры от её места в числе. Непозиционные системы Непозиционные системы, такие как унарная, египетская и римская, просты, но громоздки и неудобны для арифметических операций. Позиционные системы Позиционные системы, такие как десятичная и двоичная, компактны и позволяют легко выполнять арифметические операции. Они стали основой для кодирования информации в компьютерах. Важность двоичной системы Двоичная система с основанием 2 и алфавитом 0 и 1 является языком компьютеров. Она позволяет эффективно хранить и обрабатывать информацию, что делает её незаменимой в современных вычислительных устройствах. Ключевые идеи и выводы
THANK YOU Kimi AI 2025/01/01
