Первый слайд презентации: Составление запросов для поисковых систем
Решение задач с помощью диаграмм Эйлера – Венна
Слайд 2
Диаграммы Эйлера - Венна Диаграммы Эйлера - Венна — общее название целого ряда методов визуализации и способов графической иллюстрации, широко используемых в различных областях науки: теории множеств, теории вероятностей, логике, статистике, менеджменте, компьютерных науках. 2
Слайд 3
Леонард Эйлер Леонард Эйлер (1707—1783) Швейцарский, немецкий и российский математик и механик, внёсший фундаментальный вклад в развитие многих наук. Эйлер — автор более 850 работ по математическому анализу, дифференциальной геометрии, теории чисел, приближённым вычислениям, небесной механике, математической физике, оптике, баллистике, кораблестроению, теории музыки и другим областям. 3
Слайд 4
Круги Эйлера При решении целого ряда задач Леонард Эйлер использовал идею изображения множеств с помощью кругов. Например: А – люди В – живые существа С – неживые предметы Леонард Эйлер (1707—1783) 4
Слайд 5
Однако, ещё до Эйлера выдающийся немецкий философ и математик Готфрид Вильгельм Лейбниц использовал этот метод для геометрической интерпретации логических связей между понятиями, но всё же предпочитал использовать линейные схемы Готфрид Вильгельм фон Лейбниц (1646 - 1716) Готфрид Вильгельм Лейбниц 5
Слайд 6
Джон Венн Особенного расцвета графические методы достигли в сочинениях британским философа, математика и логика Джона Венна, изложившего их в книге «Символическая логика» в 1881 г. Поэтому такие схемы называют Диаграммы Эйлера — Венна. Венн расширил математическую логику Буля и более всего известен среди математиков и логиков за его схематический способ представления множеств и их объединений и пересечений. Джон Венн (1834—1923) 6
Слайд 7
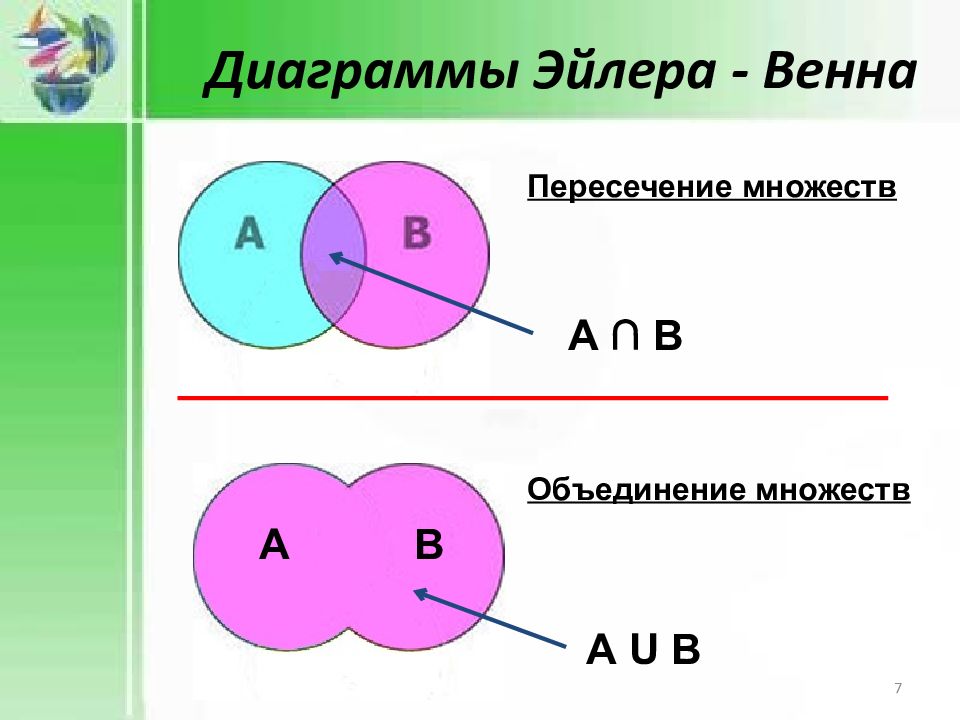
Диаграммы Эйлера - Венна А ∩ В Пересечение множеств А U В Объединение множеств А В 7
Слайд 8
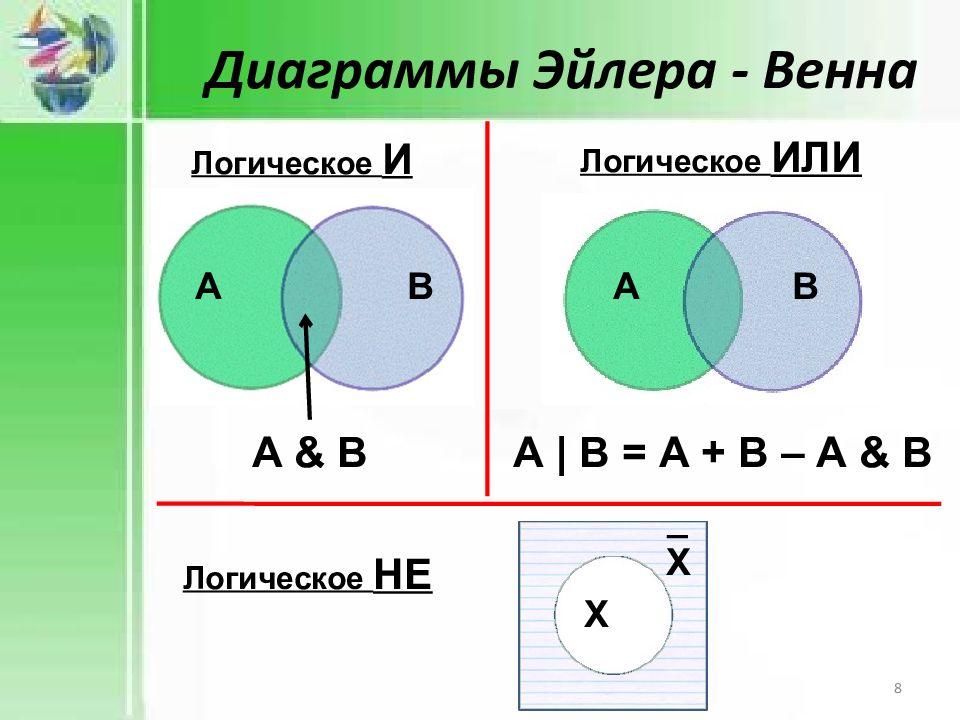
А В Диаграммы Эйлера - Венна А | В = А + В – А & В А & В Логическое И Логическое ИЛИ А В Логическое НЕ Х _ Х 8
Слайд 9
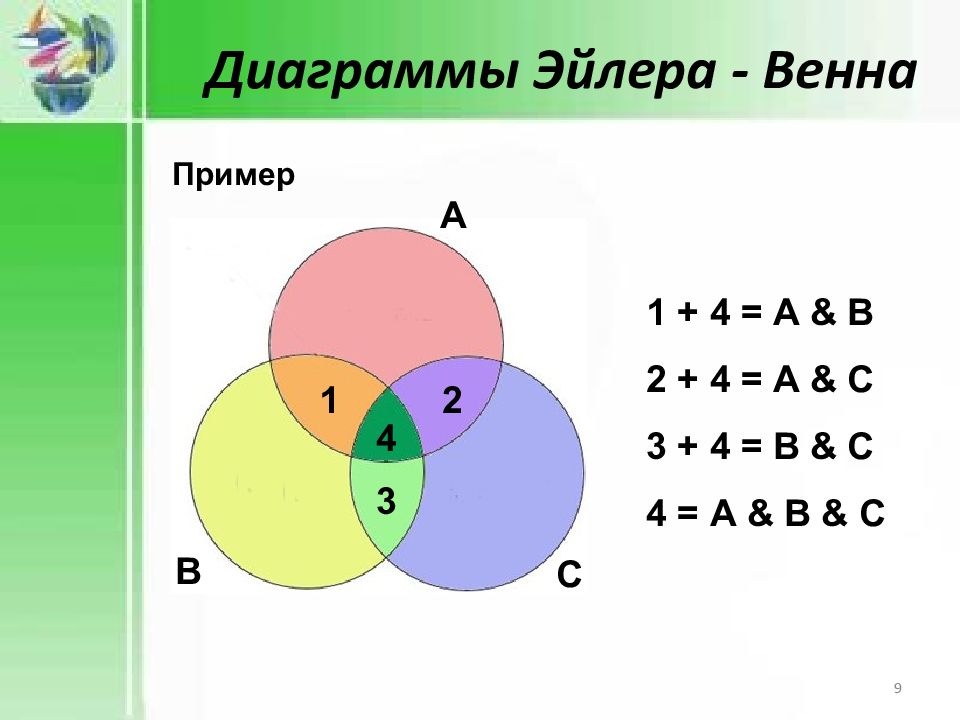
Диаграммы Эйлера - Венна 1 + 4 = А & В 2 + 4 = А & С 3 + 4 = В & С 4 = А & В & С А В С 1 2 3 4 Пример 9
Слайд 10: Задача 1
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет: Какое количество страниц (в тысячах) будет найдено по запросу Шахматы ? Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов. Задача 1 Запрос Найдено страниц (в тысячах) Шахматы | Теннис 7770 Теннис 5500 Шахматы & Теннис 1000 10
Слайд 11: Решение
Ш|Т Ш&Т Ш = (Ш|Т) – Т + (Ш & Т) = 7770 – 5500 + 1000 Ответ: 3270 Запрос Найдено страниц (в тысячах) Шахматы | Теннис 7770 Теннис 5500 Шахматы & Теннис 1000 Решение Ш Т 11
Слайд 12: Задача 2
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет: Какое количество страниц (в тысячах) будет найдено по запросу Рубин & Динамо & Спартак ? Задача 2 Запрос Найдено страниц (в тысячах) Динамо & Рубин 320 Спартак & Рубин 280 (Динамо | Спартак) & Рубин 430 12
Слайд 13: Решение
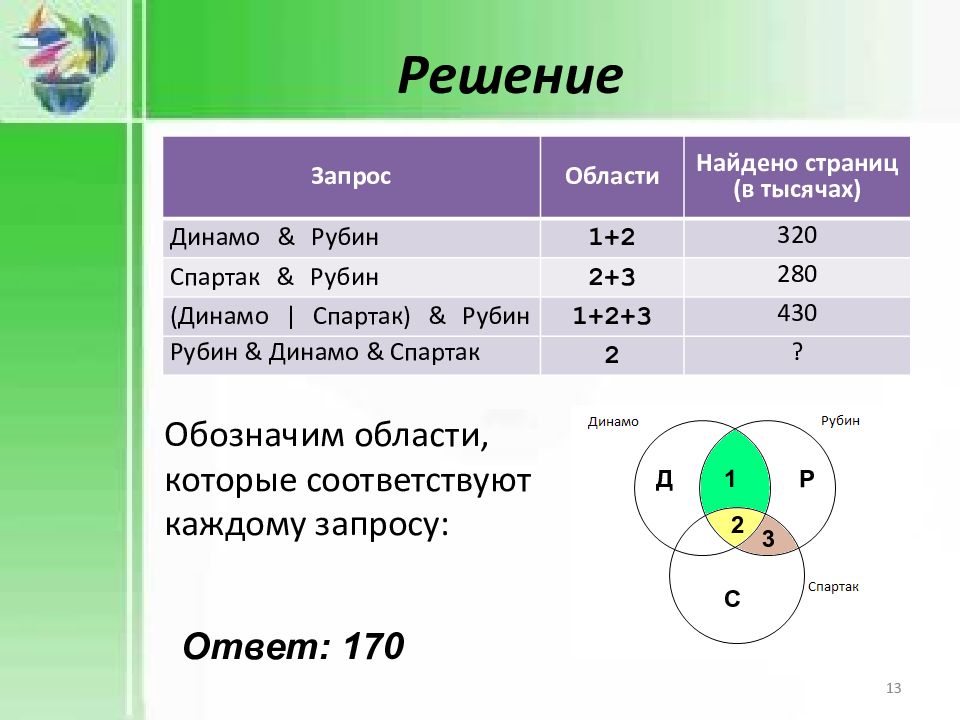
Обозначим области, которые соответствуют каждому запросу: Д 1 Р 2 3 С Ответ: 170 Запрос Области Найдено страниц (в тысячах) Динамо & Рубин 1+2 320 Спартак & Рубин 2+3 280 (Динамо | Спартак) & Рубин 1+2+3 430 Рубин & Динамо & Спартак 2 ? Решение 13
Слайд 14: Задача 3
Некоторый сегмент сети Интернет состоит из 1000 сайтов. Поисковый сервер в автоматическом режиме составил таблицу ключевых слов для сайтов этого сегмента. Вот ее фрагмент: Задача 3 Ключевое слово Количество сайтов, для которых данное слово является ключевым сканер 200 принтер 250 монитор 450 14
Слайд 15: Задача 3
Ключевое слово Количество сайтов, для которых данное слово является ключевым сканер 200 принтер 250 монитор 450 Сколько сайтов будет найдено по запросу (принтер | сканер) & монитор если было найдено: по запросу принтер | сканер 450 сайтов, по запросу принтер & монитор – 40, по запросу сканер & монитор – 50? 15
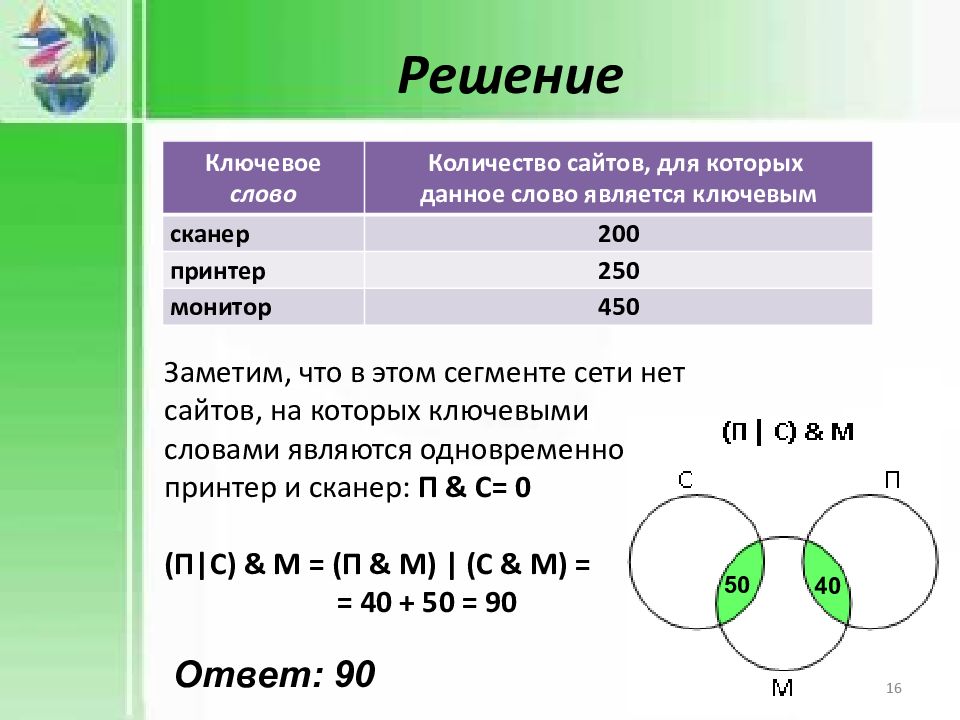
Слайд 16: Решение
Ответ: 90 Ключевое слово Количество сайтов, для которых данное слово является ключевым сканер 200 принтер 250 монитор 450 Заметим, что в этом сегменте сети нет сайтов, на которых ключевыми словами являются одновременно принтер и сканер: П & С= 0 (П | С) & М = (П & М) | (С & М) = = 40 + 50 = 90 40 50 Решение 16
Слайд 17: Задача 4
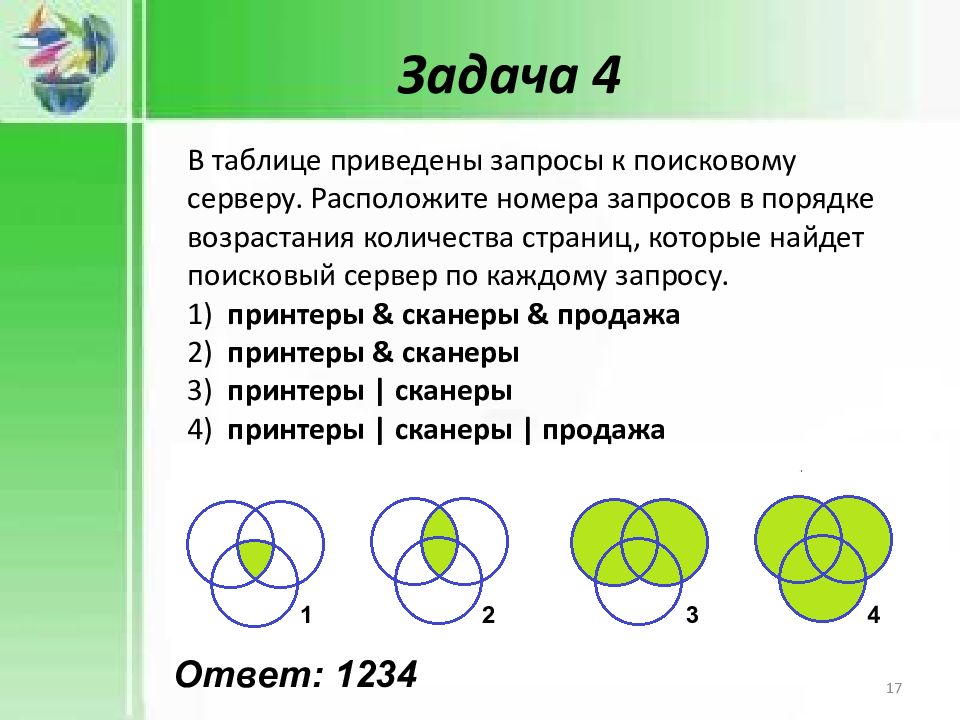
В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу. 1) принтеры & сканеры & продажа 2) принтеры & сканеры 3) принтеры | сканеры 4) принтеры | сканеры | продажа Ответ: 1234 1 2 3 4 1 2 3 4 17
Слайд 18: Задачи для тренировки
В таблице приведены запросы к поисковому серверу, условно обозначенные буквами от А до Г. Расположите запросы в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу. Ответ запишите в виде последовательности соответствующих букв. А) Гренландия & Климат & Флора & Фауна Б) Гренландия & Флора В) (Гренландия & Флора) | Фауна Г) Гренландия & Флора & Фауна В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке убывания количества страниц, которые найдет поисковый сервер по каждому запросу. 1) барокко | (классицизм & ампир) 2) барокко | классицизм 3) (классицизм & ампир) | (барокко & модерн) 4) барокко | ампир | классицизм Задачи для тренировки 18
Слайд 19: Задачи для тренировки
Некоторый сегмент сети Интернет состоит из 1000 сайтов. Поисковый сервер составил таблицу ключевых слов для сайтов этого сегмента. Вот ее фрагмент: Сколько сайтов будет найдено по запросу сомики | меченосцы | гуппи, если по запросу сомики & гуппи было найдено 0 сайтов, по запросу сомики & меченосцы – 20, а по запросу меченосцы & гуппи – 10 ? Ключевое слово Количество сайтов, для которых данное слово является ключевым сомики 250 меченосцы 200 гуппи 500 Задачи для тренировки 19
Слайд 20: Задачи для тренировки
В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета: Сколько страниц (в тысячах) будет найдено по запросу Атос & ( Портос | Арамис )? Запрос Количество страниц (тыс.) Атос & Портос 335 Атос & Арамис 235 Атос & Портос & Арамис 120 Задачи для тренировки 20
Слайд 21
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет: Сколько страниц (в тысячах) будет найдено по запросу март & апрель & май ? Запрос Найдено страниц (в тысячах) март & май 472 май & апрель 42 5 май & (март | апрель ) 6 20 Задачи для тренировки 21
Слайд 23
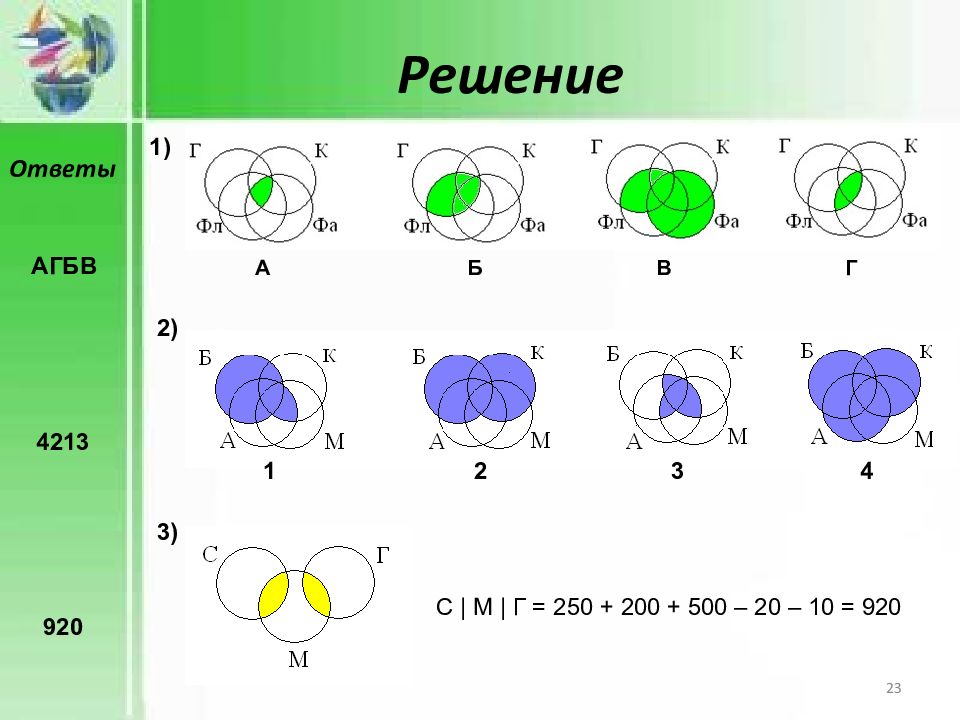
Решение 1) 2) А Б В Г 3) 1 2 3 4 АГБВ 4213 С | М | Г = 250 + 200 + 500 – 20 – 10 = 920 920 Ответы 23
Слайд 24
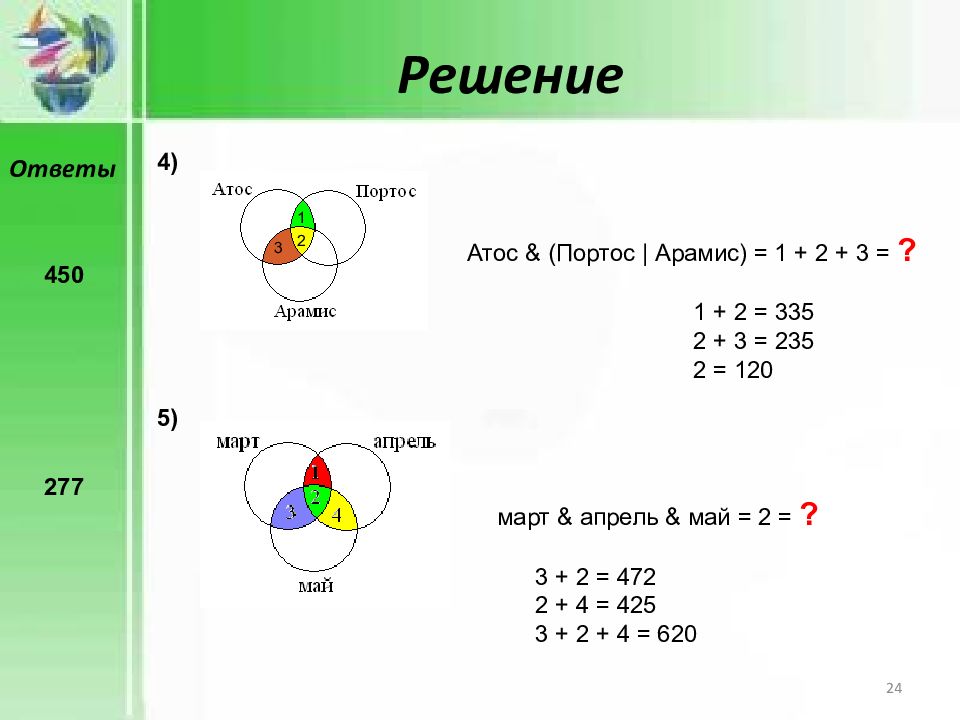
4) Решение 5) 1 2 3 Атос & ( Портос | Арамис ) = 1 + 2 + 3 = ? 1 + 2 = 335 2 + 3 = 235 2 = 120 450 277 март & апрель & май = 2 = ? 3 + 2 = 472 2 + 4 = 425 3 + 2 + 4 = 620 Ответы 24
Последний слайд презентации: Составление запросов для поисковых систем: Источники информации
Акимов О.Е., Дискретная математика. Операции логики Буля. Официальный информационный портал ЕГЭ www. ege. edu. ru Преподавание, наука и жизнь. http://kpolyakov.spb.ru http://www.wikiznanie.ru http://ru.wikipedia.org/wiki 25