Первый слайд презентации: Структуры и алгоритмы обработки данных на ЭВМ АВЛ-дерево
Красиков И.А. ТУСУР 2015
Слайд 2: Задачи
Дать определение АВЛ-дерева; Рассмотреть способы балансировки АВЛ-дерева; Научиться выполнять построение АВЛ-дерева; Научиться выполнять операции поиска, добавления, удаления узла из АВЛ-дерева. Задачи
Слайд 3: Определение
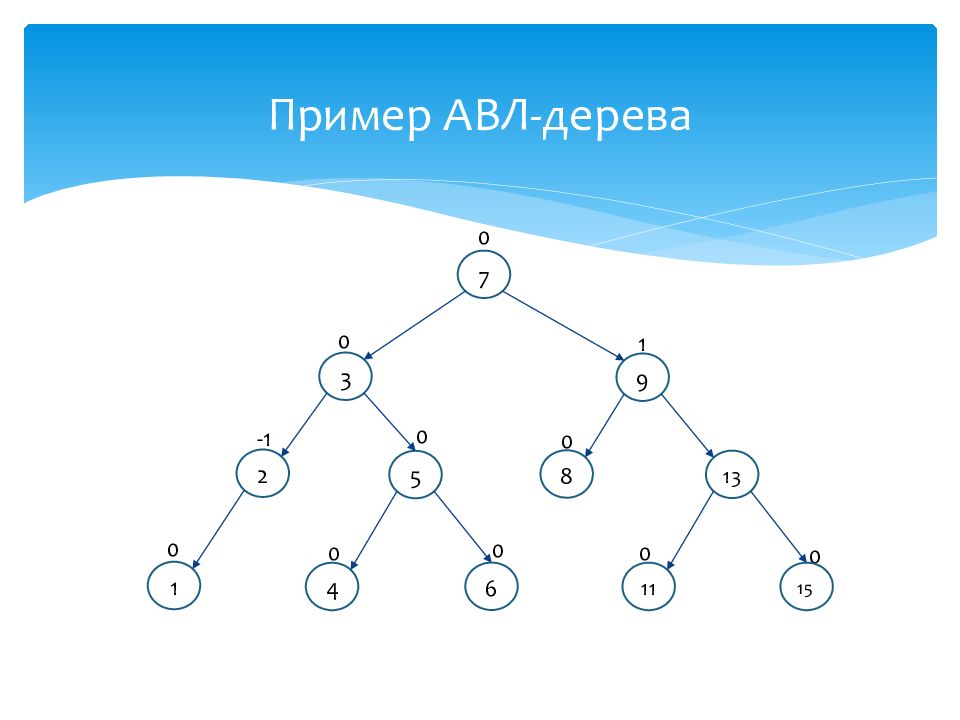
АВЛ–дерево - это структура данных, изобретенная советскими математиками: Г.М. Андельсон -Вельским и Е.М. Ландисом. АВЛ – дерево является частным случаем двоичного дерева поиска, для которого определено следующее условие: каждый узел дерева имеет коэффициент сбалансированности, который должен удовлетворять условию | h ( Rtree ) - h ( Ltree ) | ≤ 1, где h ( Ltree ) и h ( Rtree ) – высоты левого и правого поддеревьев соответственно. Т.е. коэффициент сбалансированности для каждого узла дерева должен принимать одно из трех значений {-1,0,1}. Если, хотя бы для одного узла это условие не выполняется, то дерево не является сбалансированным по АВЛ и необходима его балансировка. Кроме того, поскольку АВЛ-дерево является бинарным деревом поиска, то для каждого его узла должно выполняться условие: значения в левом поддереве должны быть меньше значения этого узла, а значения в правом поддереве должны быть больше значения данного узла. Сложность операций поиска, добавления, удаления узла в АВЛ-дереве составляет порядка О( log N ), где N – количество элементов дерева. Определение
Слайд 5: Структура АВЛ-дерева
struct Tree { int Value; Tree *Right, *Left ; }; Структура АВЛ-дерева В рассматриваемых примерах программная структура АВЛ-дерева будет иметь следующий вид:
Слайд 6: Балансировка АВЛ-дерева LL - вращение
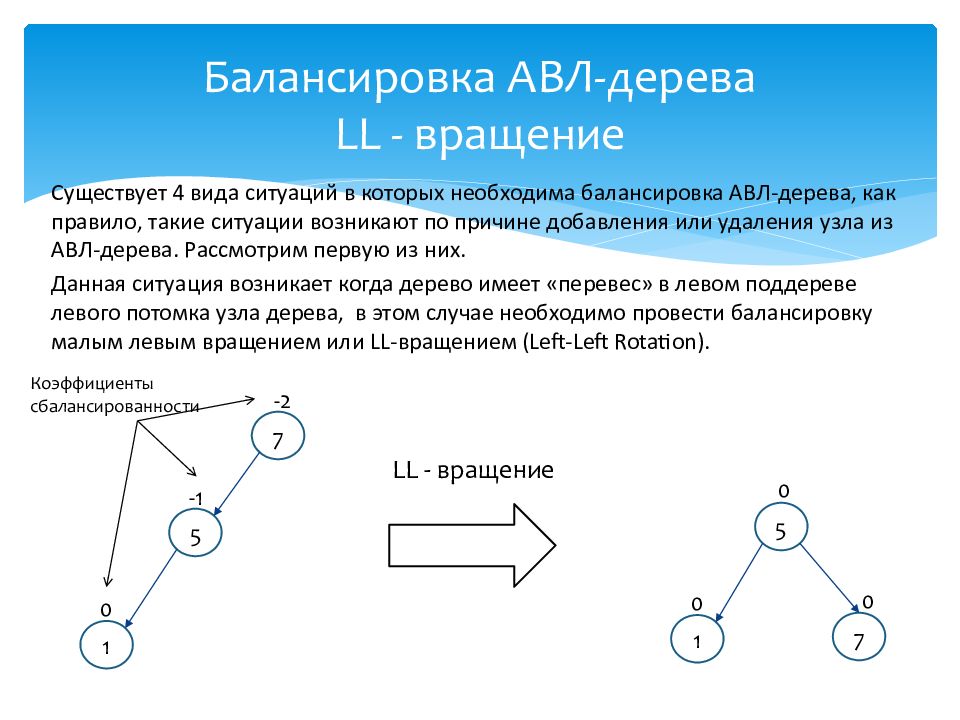
Существует 4 вида ситуаций в которых необходима балансировка АВЛ-дерева, как правило, такие ситуации возникают по причине добавления или удаления узла из АВЛ-дерева. Рассмотрим первую из них. Данная ситуация возникает когда дерево имеет «перевес» в левом поддереве левого потомка узла дерева, в этом случае необходимо провести балансировку малым левым вращением или LL- вращением ( Left-Left Rotation ). 7 5 1 0 -1 -2 7 5 1 0 0 0 Коэффициенты сбалансированности LL - вращение
Слайд 7: Балансировка АВЛ-дерева LL - вращение
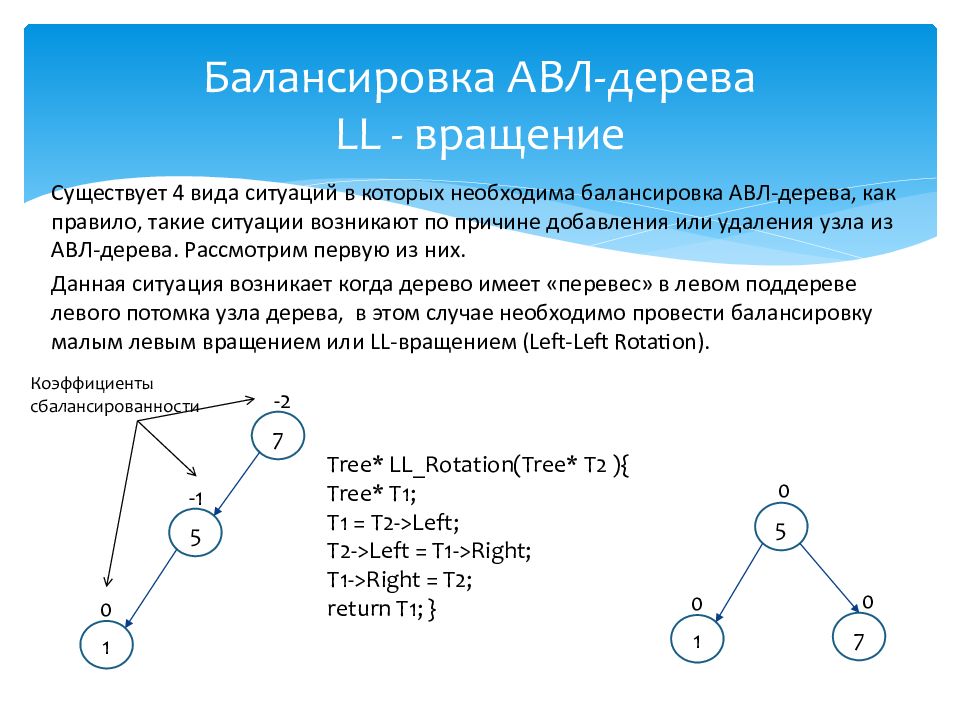
Tree * LL_Rotation(Tree* T2 ){ Tree * T1; T1 = T2->Left; T2- >Left = T1->Right; T1- >Right = T2; return T1 ; } Балансировка АВЛ-дерева LL - вращение Существует 4 вида ситуаций в которых необходима балансировка АВЛ-дерева, как правило, такие ситуации возникают по причине добавления или удаления узла из АВЛ-дерева. Рассмотрим первую из них. Данная ситуация возникает когда дерево имеет «перевес» в левом поддереве левого потомка узла дерева, в этом случае необходимо провести балансировку малым левым вращением или LL- вращением ( Left-Left Rotation ). 7 5 1 0 -1 -2 7 5 1 0 0 0 Коэффициенты сбалансированности
Слайд 8: Балансировка АВЛ-дерева RR - вращение
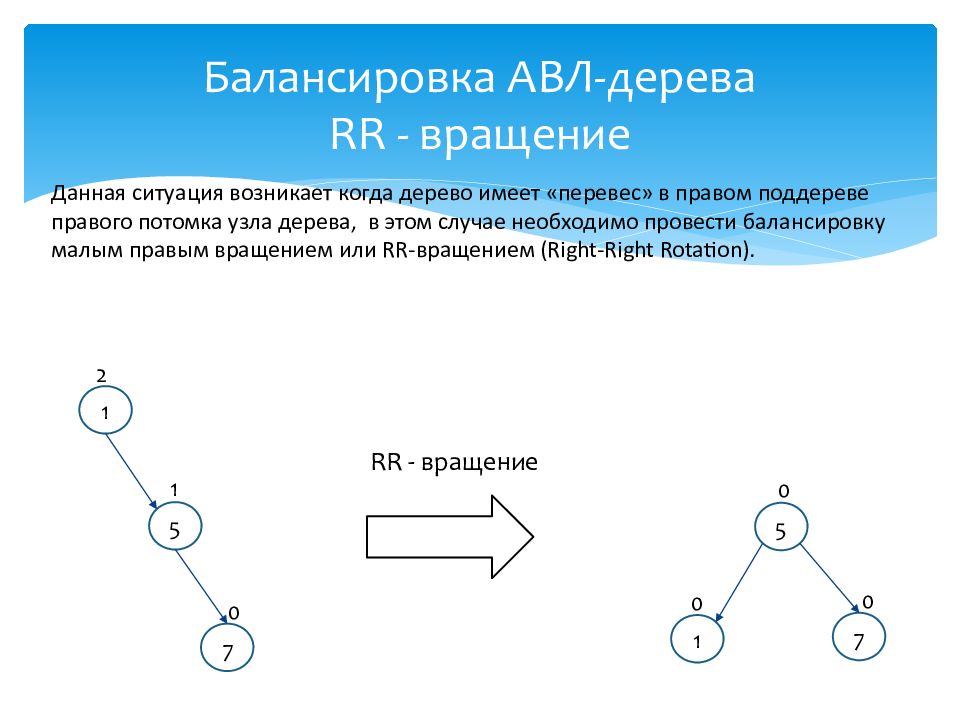
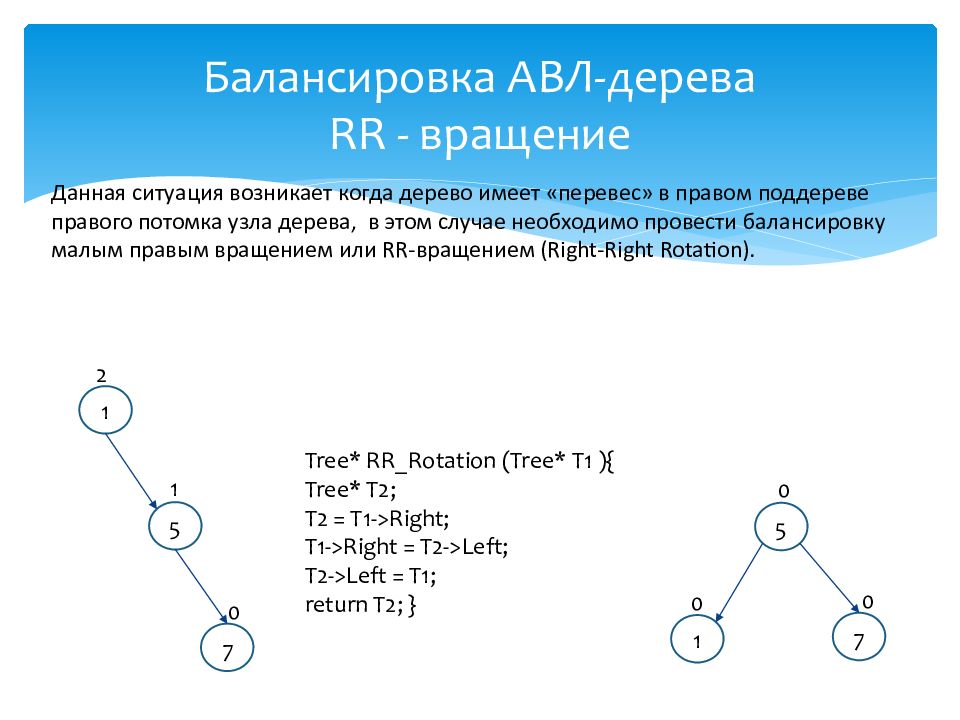
Данная ситуация возникает когда дерево имеет «перевес» в правом поддереве правого потомка узла дерева, в этом случае необходимо провести балансировку малым правым вращением или RR- вращением ( Right-Right Rotation ). 1 5 7 0 1 2 7 5 1 0 0 0 RR - вращение
Слайд 9: Балансировка АВЛ-дерева RR - вращение
Данная ситуация возникает когда дерево имеет «перевес» в правом поддереве правого потомка узла дерева, в этом случае необходимо провести балансировку малым правым вращением или RR- вращением ( Right-Right Rotation ). 1 5 7 0 1 2 7 5 1 0 0 0 Tree* RR_Rotation (Tree* T1 ){ Tree* T2; T2 = T1->Right; T1->Right = T2->Left; T2->Left = T1; return T2; }
Слайд 10: Балансировка АВЛ-дерева LR - вращение
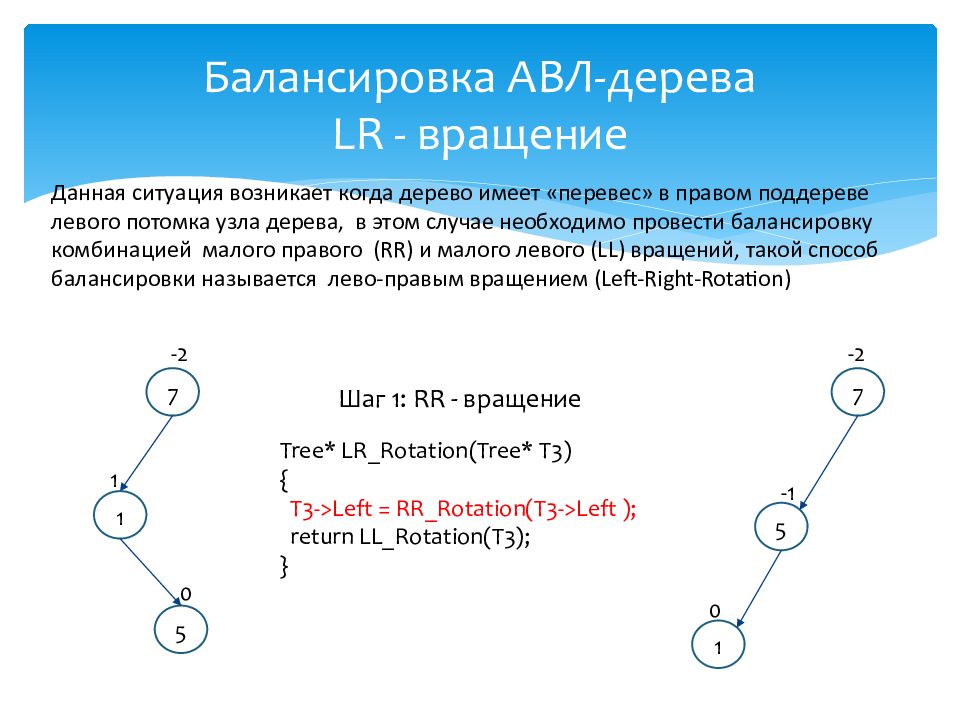
Данная ситуация возникает когда дерево имеет «перевес» в правом поддереве левого потомка узла дерева, в этом случае необходимо провести балансировку комбинацией малого правого ( RR ) и малого левого ( LL ) вращений, такой способ балансировки называется лево-правым вращением ( Left-Right-Rotation) 7 1 5 0 1 - 2 7 5 1 0 -2 -1 Шаг 1: RR - вращение Tree* LR_Rotation (Tree* T3) { T3->Left = RR_Rotation(T3->Left ); return LL_Rotation(T3); }
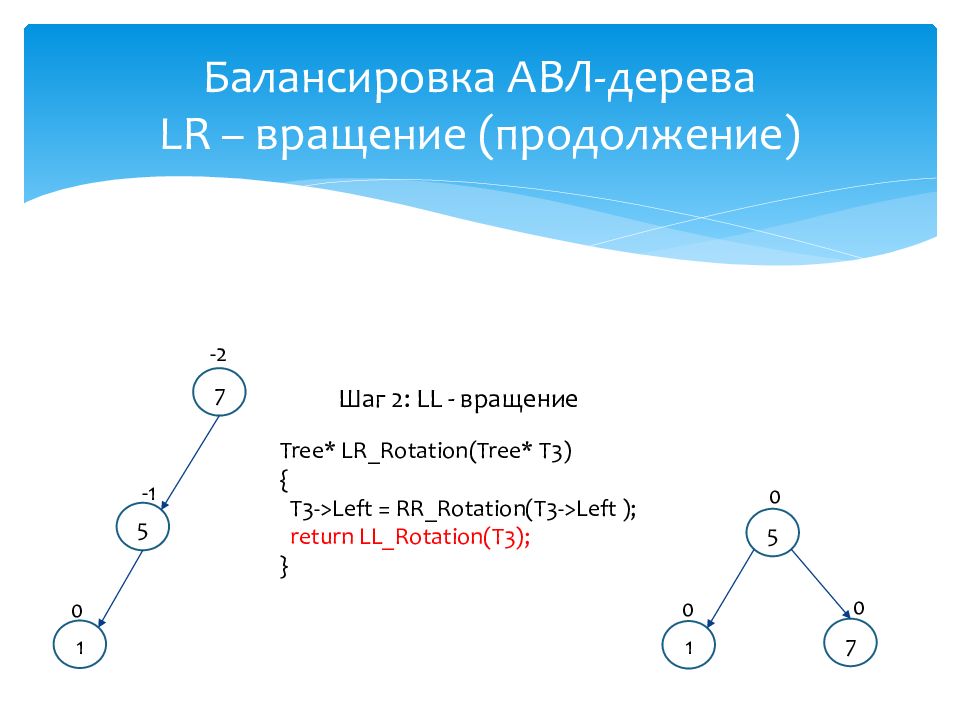
7 5 1 0 -2 -1 Шаг 2 : LL - вращение Tree* LR_Rotation (Tree* T3) { T3->Left = RR_Rotation(T3->Left ); return LL_Rotation(T3); } 7 5 1 0 0 0
Слайд 12: Балансировка АВЛ-дерева R L - вращение
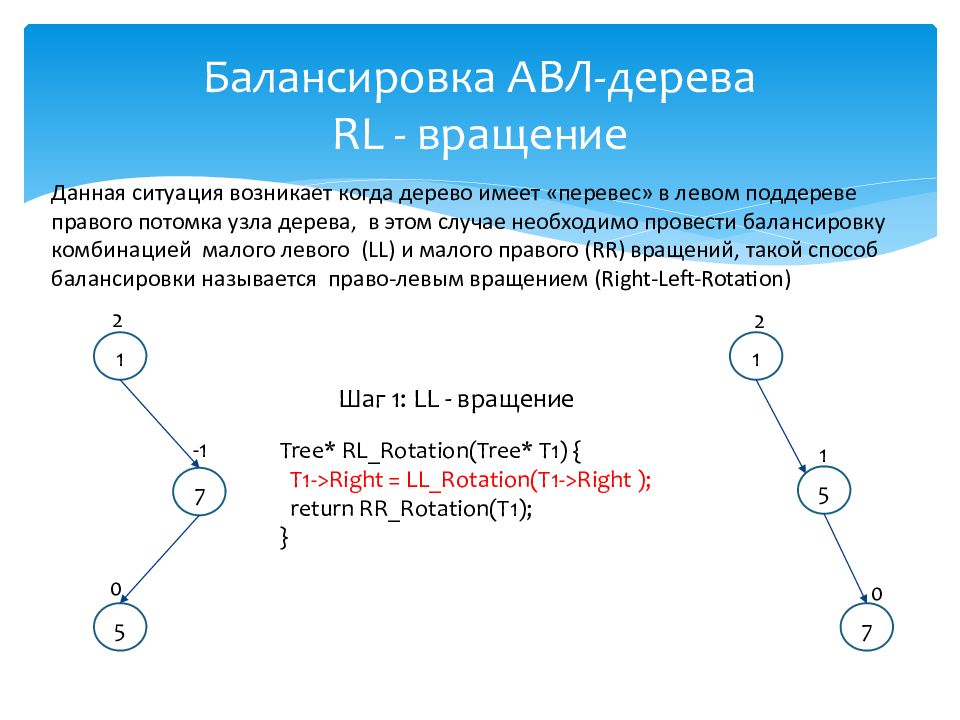
Данная ситуация возникает когда дерево имеет «перевес» в левом поддереве правого потомка узла дерева, в этом случае необходимо провести балансировку комбинацией малого левого ( LL ) и малого правого ( RR ) вращений, такой способ балансировки называется право-левым вращением ( Right-Left-Rotation) 1 7 5 0 - 1 2 1 5 7 0 2 1 Шаг 1: LL - вращение Tree* RL_Rotation (Tree* T1) { T1->Right = LL_Rotation(T1->Right ); return RR_Rotation(T1); }
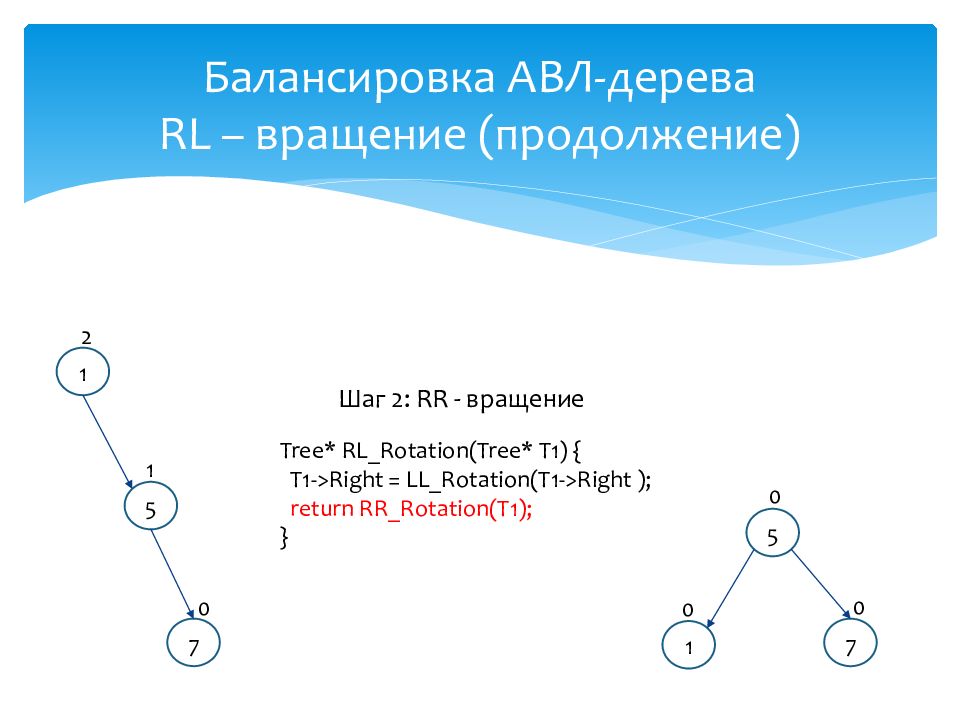
Слайд 13: Балансировка АВЛ-дерева RL – вращение (продолжение)
Шаг 2 : RR - вращение Tree* RL_Rotation (Tree* T1) { T1->Right = LL_Rotation(T1->Right ); return RR_Rotation(T1); } 7 5 1 0 0 0 1 5 7 0 2 1
Слайд 14: Построение АВЛ-дерева
1 0 Рассмотрим процесс построения АВЛ-дерева, состоящего из последовательности чисел: 1, 15, 7, 2, 3, 4, 9, 8, 5, 6, 11, 13 Новый
Слайд 15: Построение АВЛ-дерева
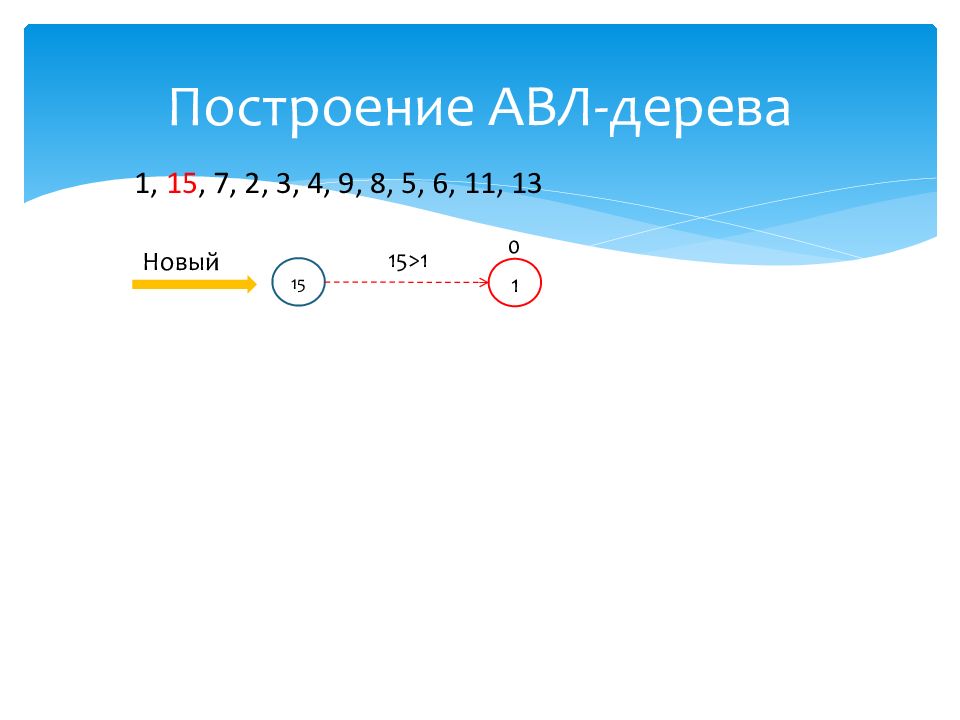
1 0 Новый 15 15 >1 1, 15, 7, 2, 3, 4, 9, 8, 5, 6, 11, 13
Слайд 16: Построение АВЛ-дерева
1 0 Новый 15 15 1, 15, 7, 2, 3, 4, 9, 8, 5, 6, 11, 13
Слайд 17: Построение АВЛ-дерева
1 1 Новый 7 15 0 7 >1 1, 15, 7, 2, 3, 4, 9, 8, 5, 6, 11, 13
Слайд 18: Построение АВЛ-дерева
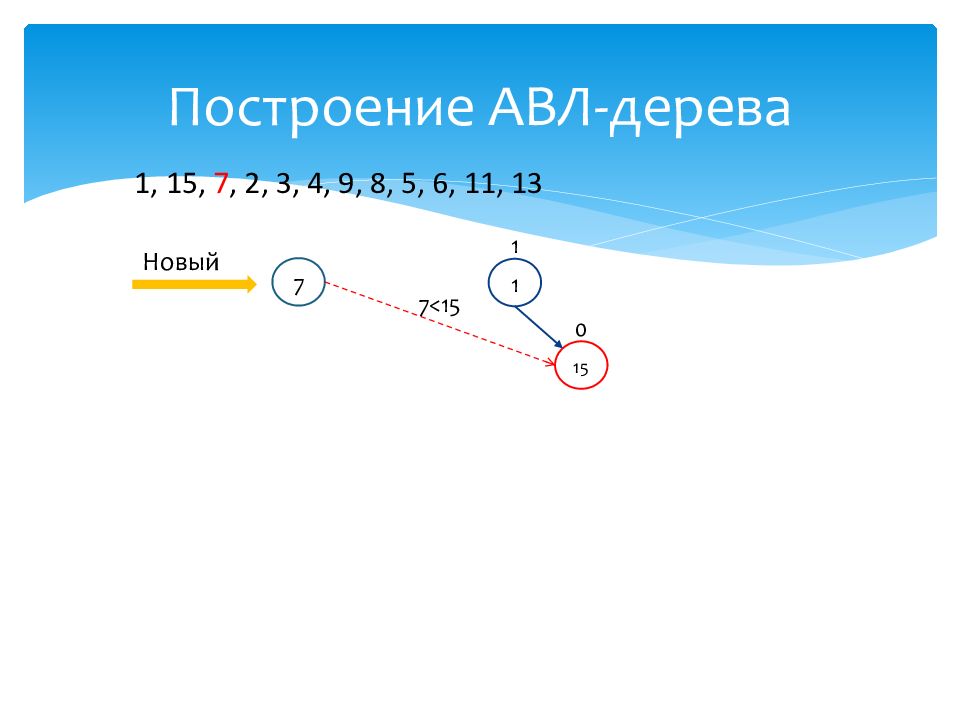
1 1 Новый 7 15 0 7<15 1, 15, 7, 2, 3, 4, 9, 8, 5, 6, 11, 13
Слайд 19: Построение АВЛ-дерева
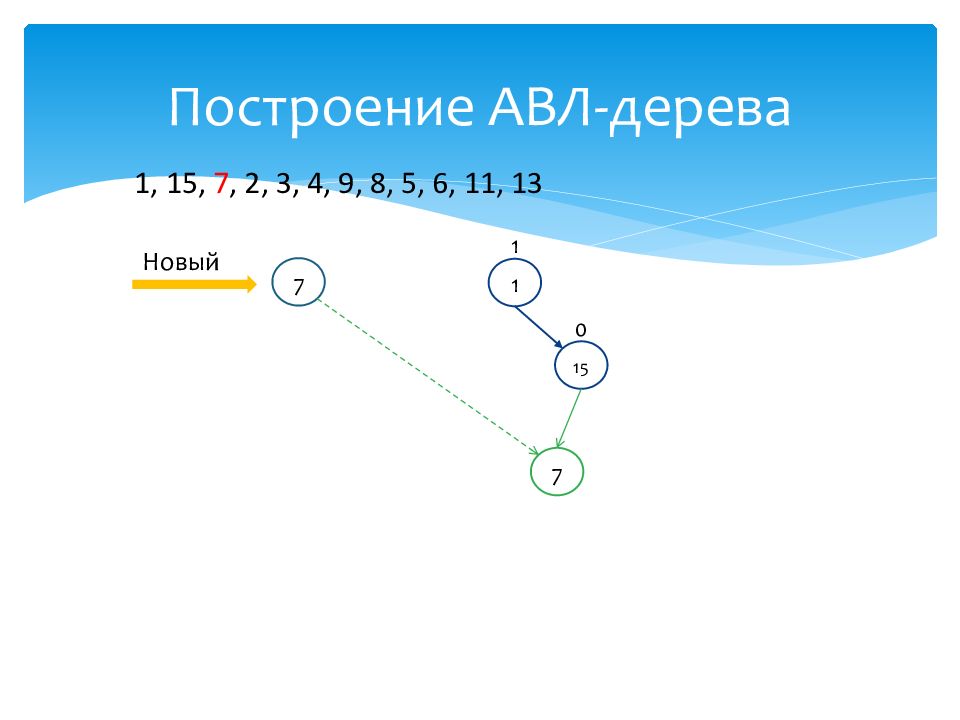
1 1 Новый 7 15 0 7 1, 15, 7, 2, 3, 4, 9, 8, 5, 6, 11, 13
Слайд 20: Построение АВЛ-дерева
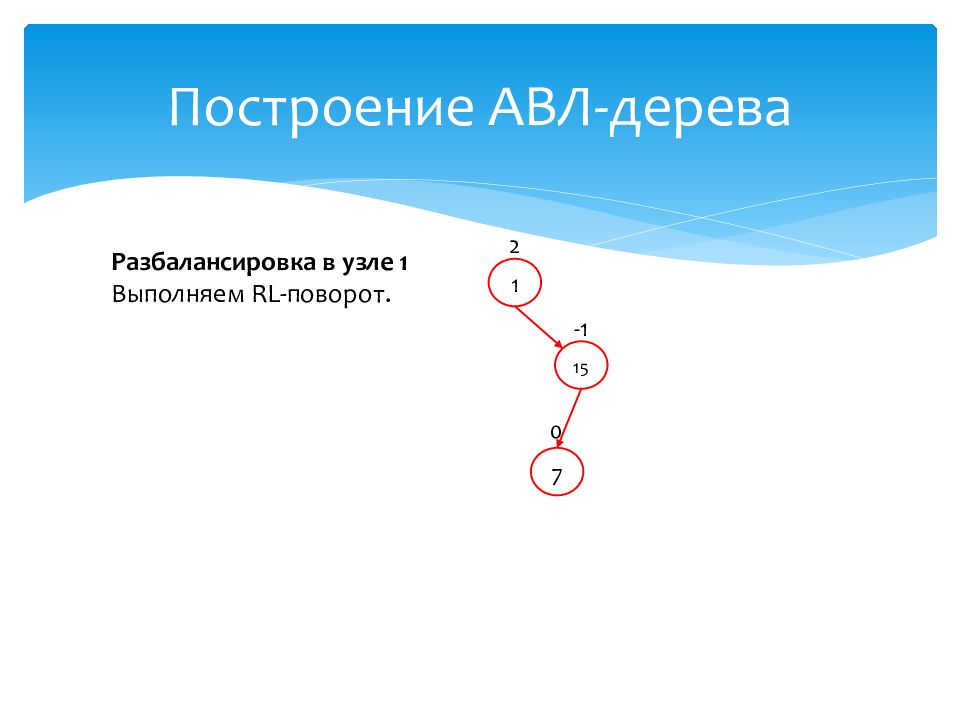
1 2 15 -1 7 0 Разбалансировка в узле 1 Выполняем RL- поворот.
Слайд 21: Построение АВЛ-дерева
1 0 15 0 7 0 Новый 2 2 < 7 1, 15, 7, 2, 3, 4, 9, 8, 5, 6, 11, 13
Слайд 22: Построение АВЛ-дерева
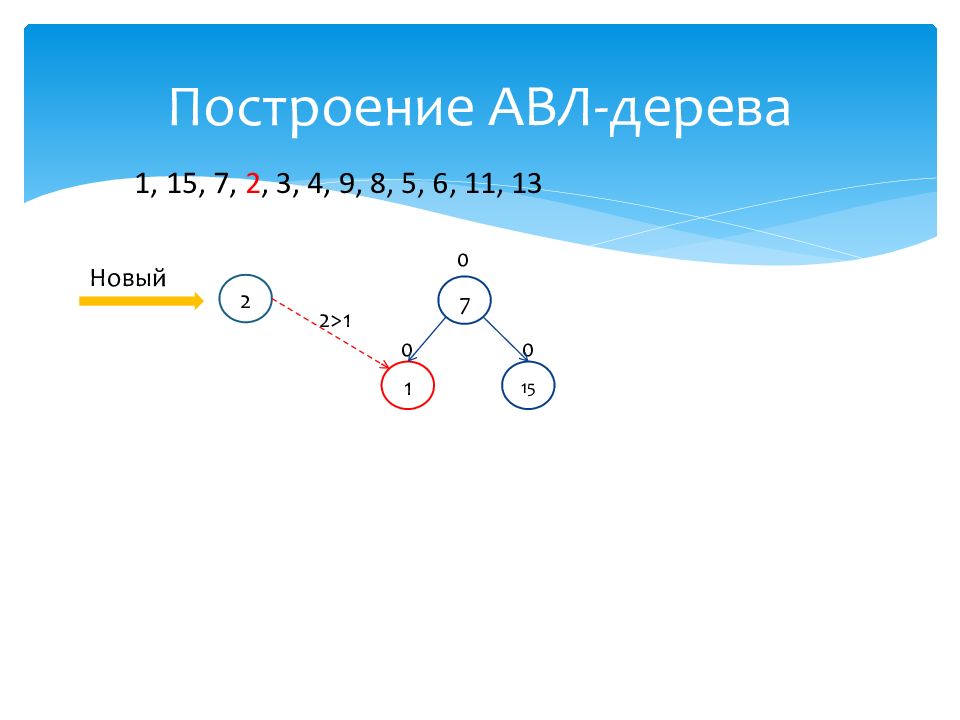
1 0 15 0 7 0 Новый 2 2 > 1 1, 15, 7, 2, 3, 4, 9, 8, 5, 6, 11, 13
Слайд 23: Построение АВЛ-дерева
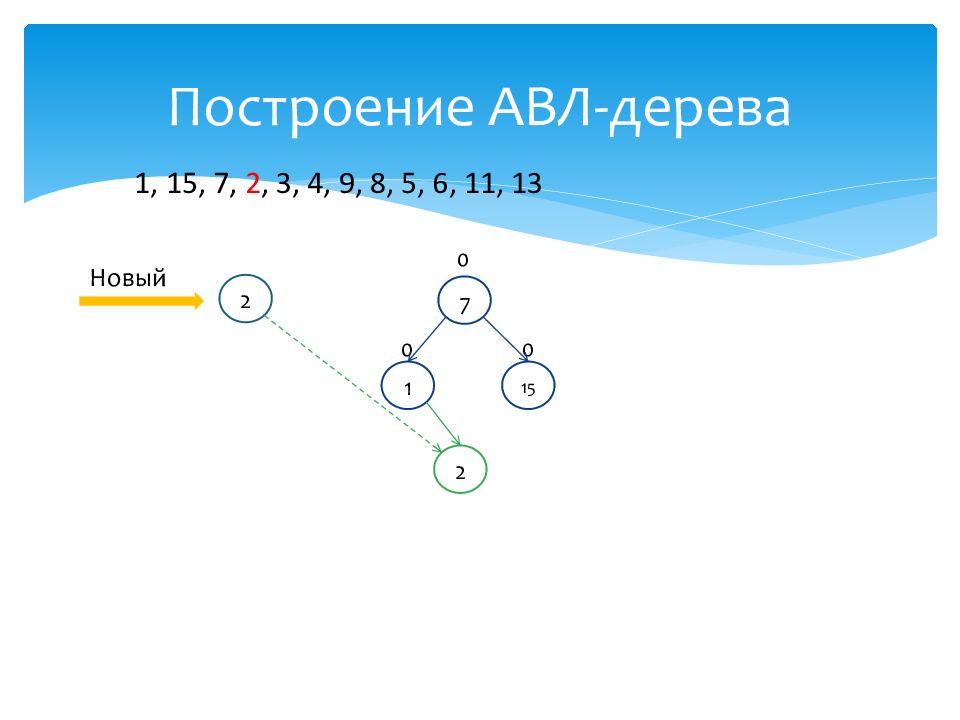
1 0 15 0 7 0 Новый 2 2 1, 15, 7, 2, 3, 4, 9, 8, 5, 6, 11, 13
Слайд 24: Построение АВЛ-дерева
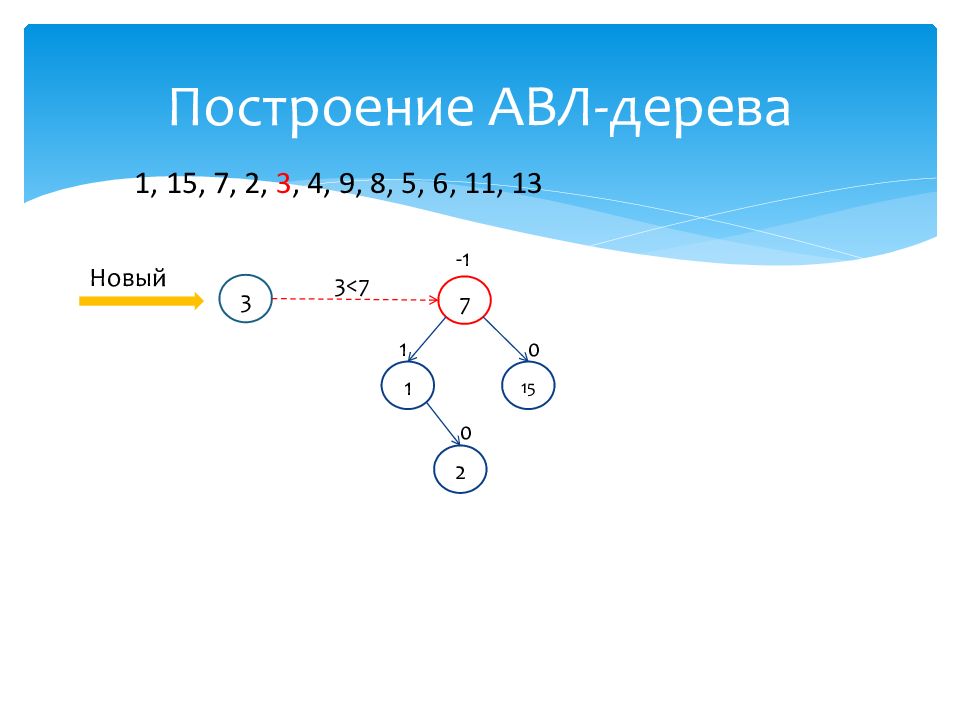
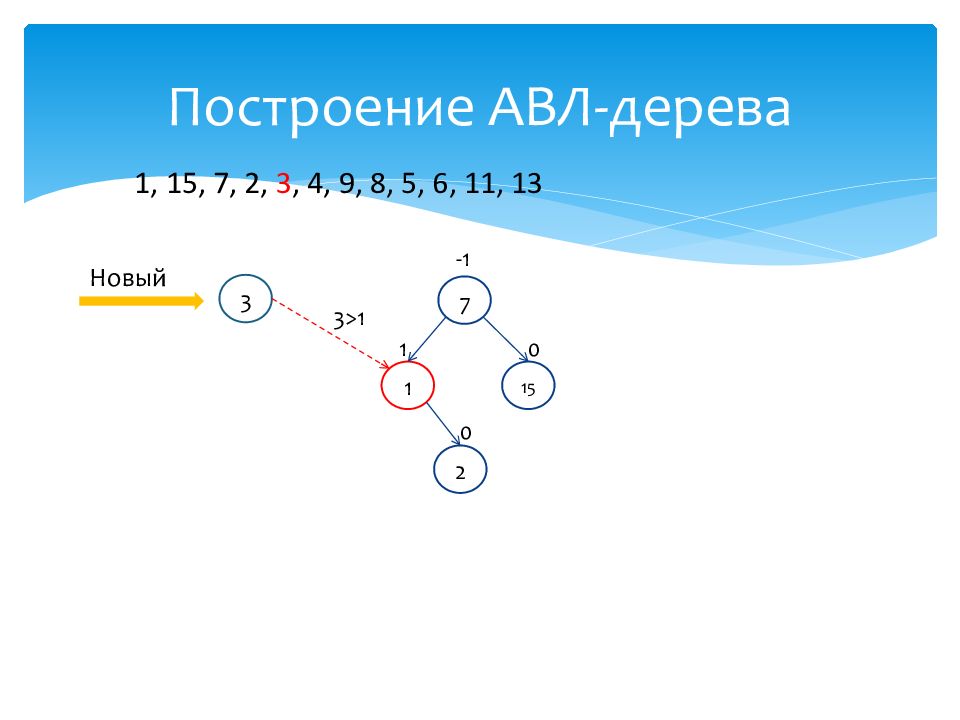
1 1 15 0 7 -1 2 0 1, 15, 7, 2, 3, 4, 9, 8, 5, 6, 11, 13 Новый 3 3<7
Слайд 25: Построение АВЛ-дерева
1 1 15 0 7 -1 2 0 1, 15, 7, 2, 3, 4, 9, 8, 5, 6, 11, 13 Новый 3 3 >1
Слайд 26: Построение АВЛ-дерева
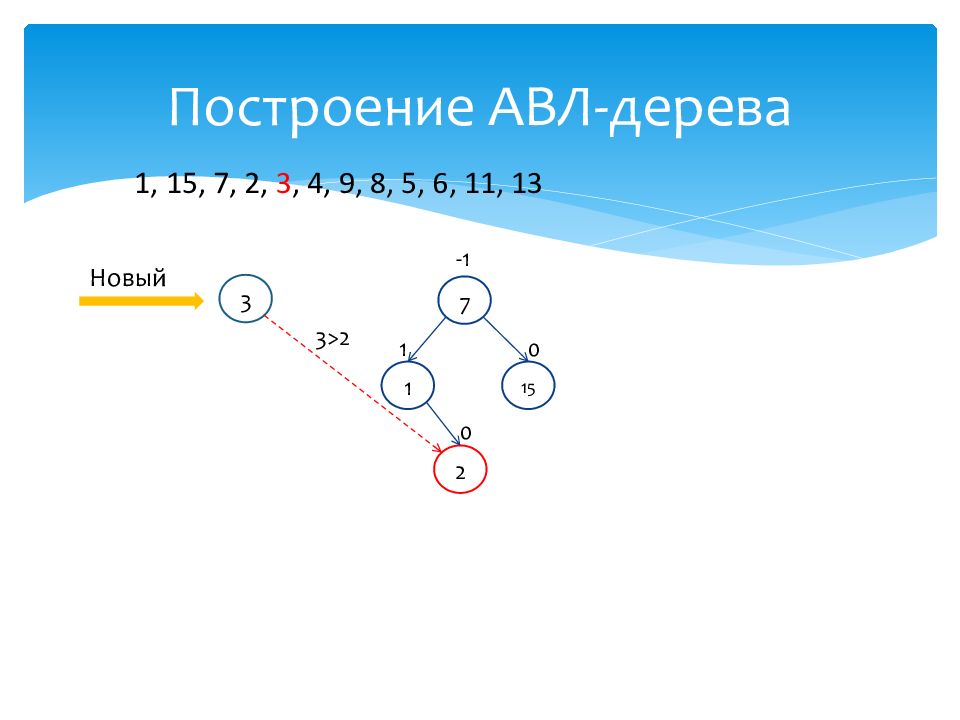
1 1 15 0 7 -1 2 0 1, 15, 7, 2, 3, 4, 9, 8, 5, 6, 11, 13 Новый 3 3>2
Слайд 27: Построение АВЛ-дерева
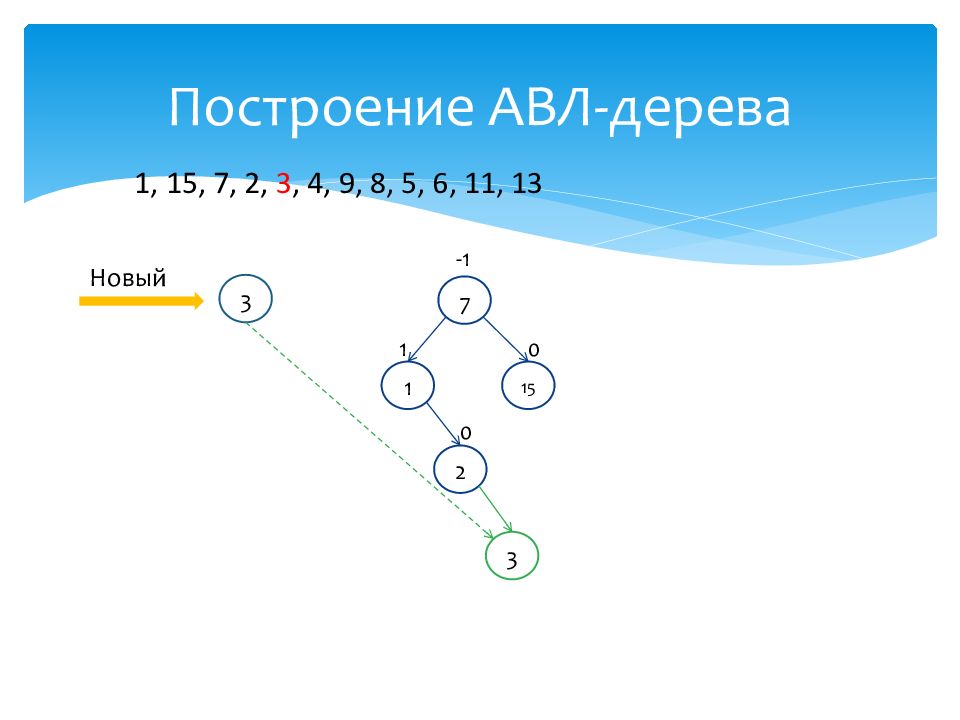
1 1 15 0 7 -1 2 0 1, 15, 7, 2, 3, 4, 9, 8, 5, 6, 11, 13 Новый 3 3
Слайд 28: Построение АВЛ-дерева
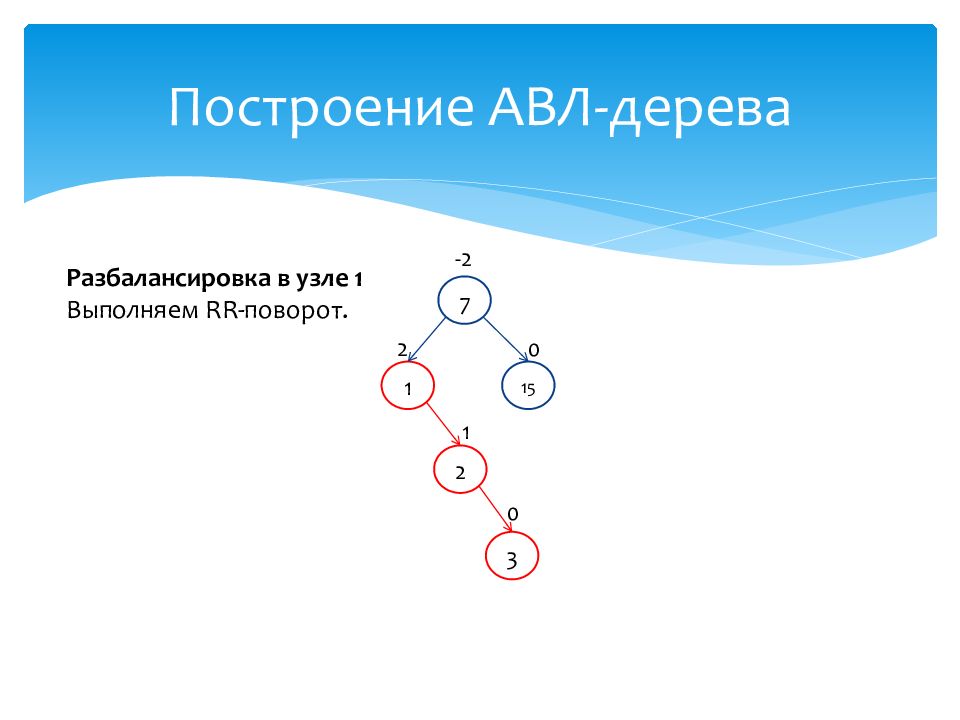
1 2 15 0 7 -2 2 1 3 0 Разбалансировка в узле 1 Выполняем RR- поворот.
Слайд 29: Построение АВЛ-дерева
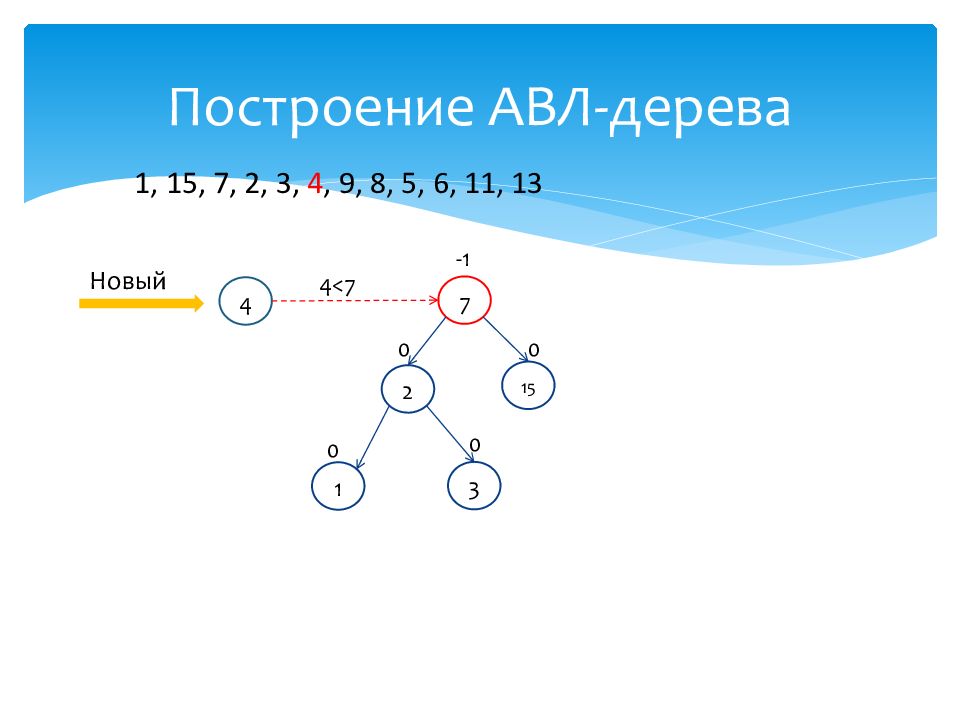
1 0 15 0 7 -1 2 0 3 0 Новый 4 4<7 1, 15, 7, 2, 3, 4, 9, 8, 5, 6, 11, 13
Слайд 30: Построение АВЛ-дерева
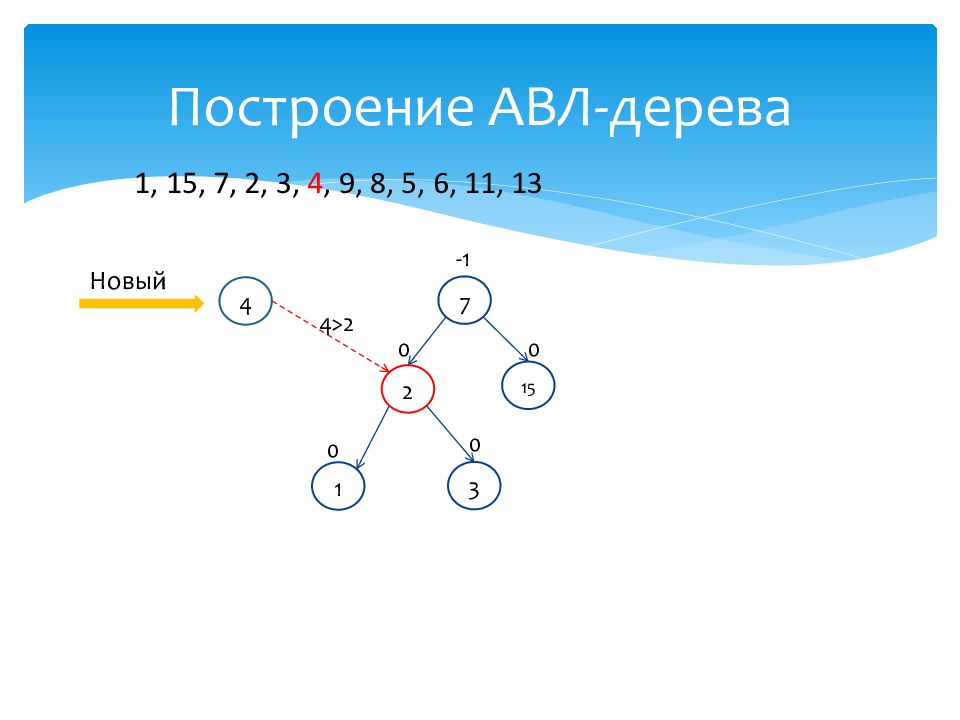
1 0 15 0 7 -1 2 0 3 0 Новый 4 4>2 1, 15, 7, 2, 3, 4, 9, 8, 5, 6, 11, 13
Слайд 31: Построение АВЛ-дерева
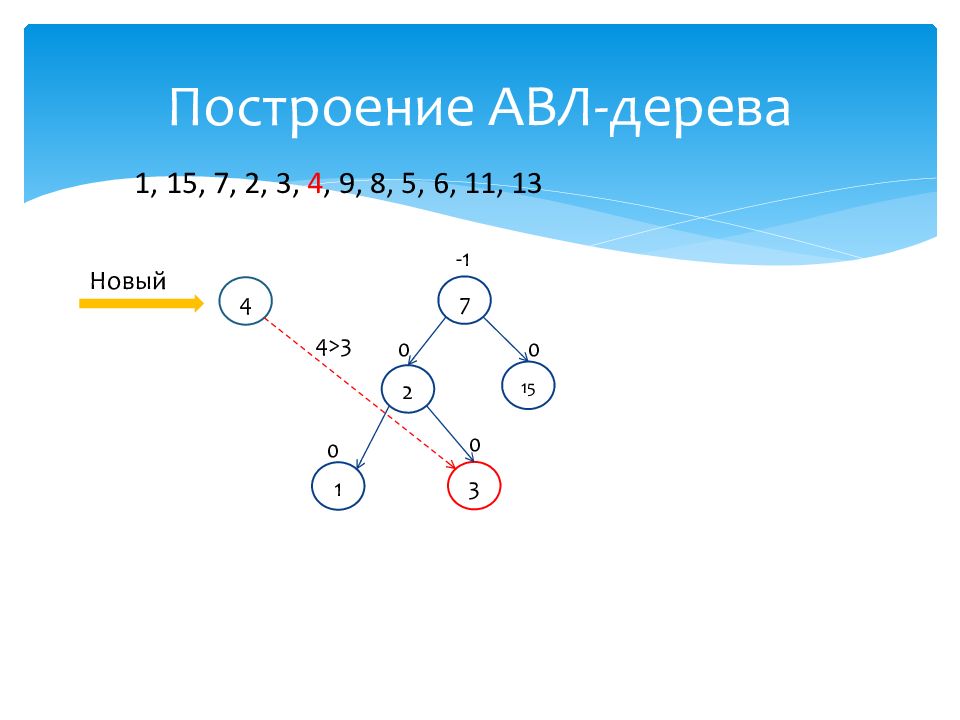
1 0 15 0 7 -1 2 0 3 0 Новый 4 4>3 1, 15, 7, 2, 3, 4, 9, 8, 5, 6, 11, 13
Слайд 32: Построение АВЛ-дерева
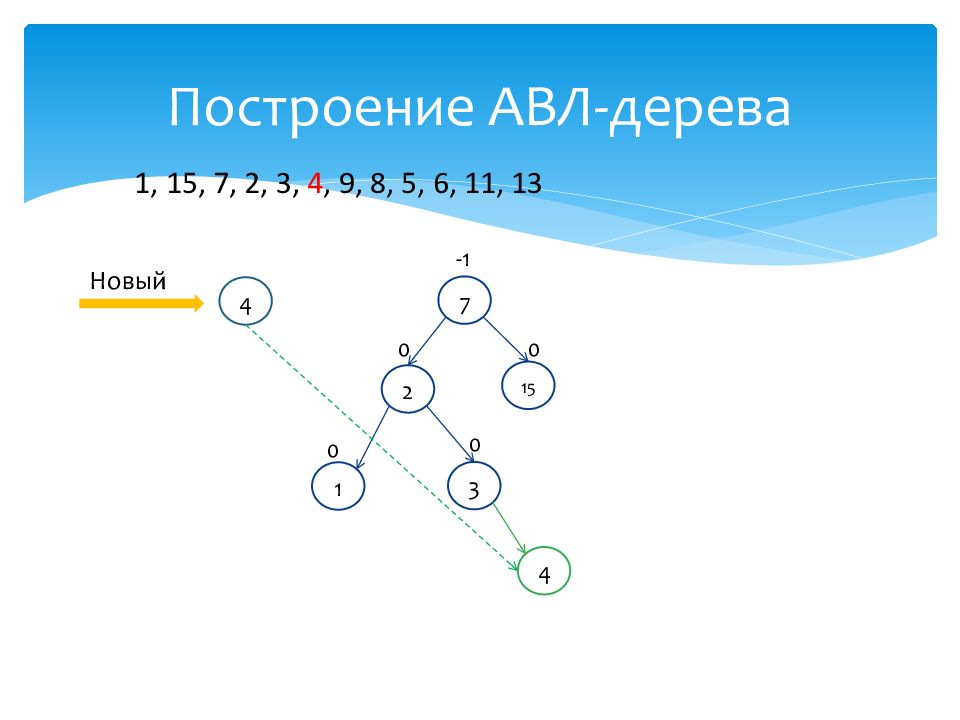
1 0 15 0 7 -1 2 0 3 0 Новый 4 1, 15, 7, 2, 3, 4, 9, 8, 5, 6, 11, 13 4
Слайд 33: Построение АВЛ-дерева
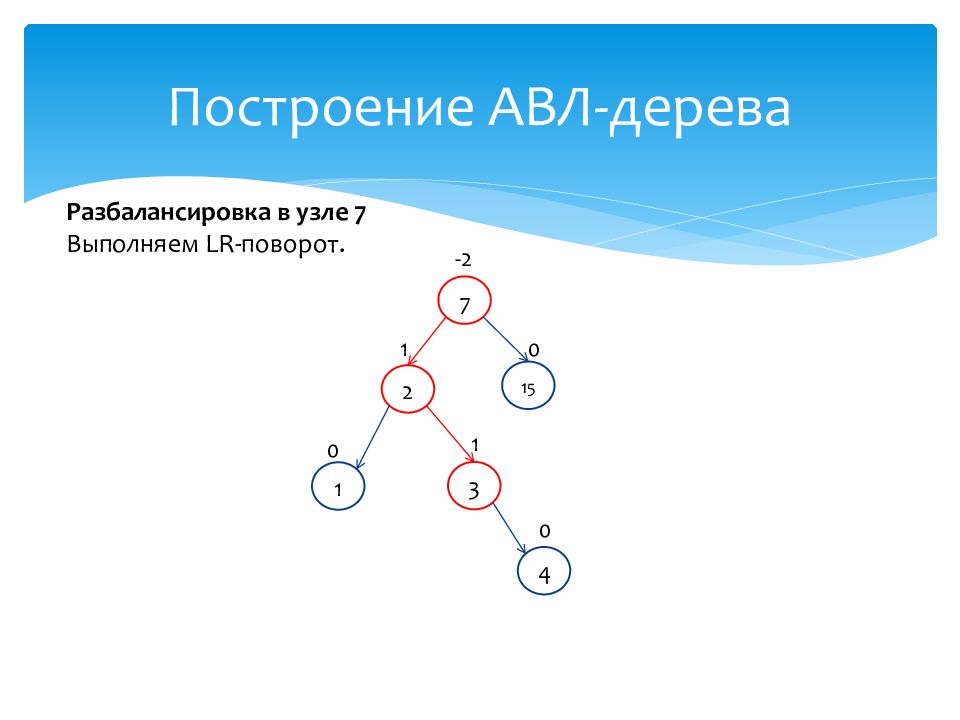
1 0 15 0 7 -2 2 1 3 1 4 0 Разбалансировка в узле 7 Выполняем L R- поворот.
Слайд 34: Построение АВЛ-дерева
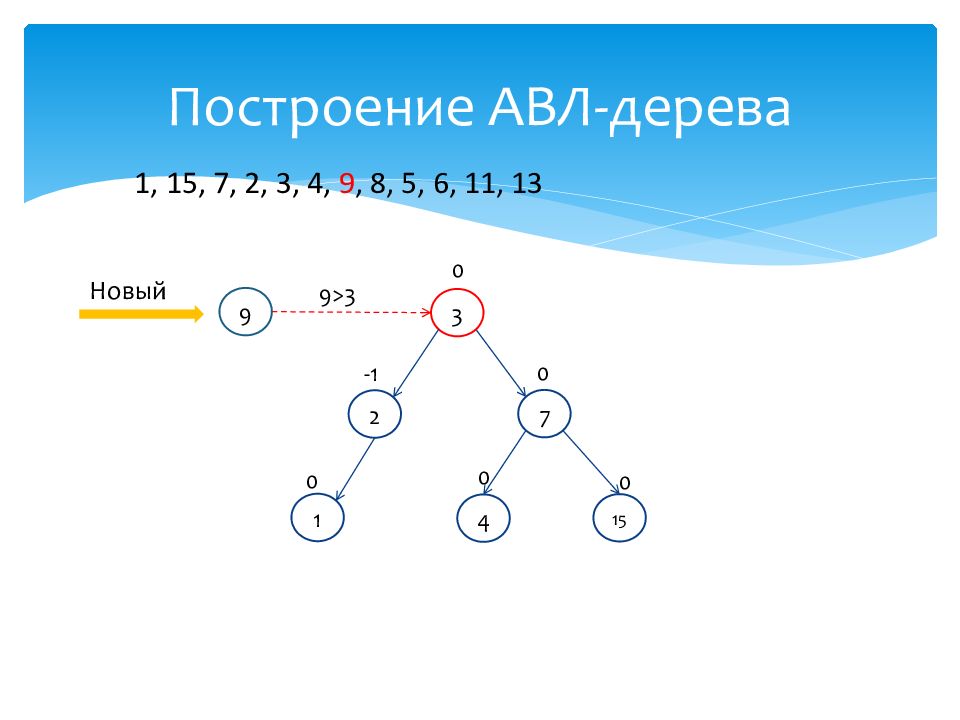
1 0 15 0 7 0 2 -1 3 0 4 0 Новый 9 9>3 1, 15, 7, 2, 3, 4, 9, 8, 5, 6, 11, 13
Слайд 35: Построение АВЛ-дерева
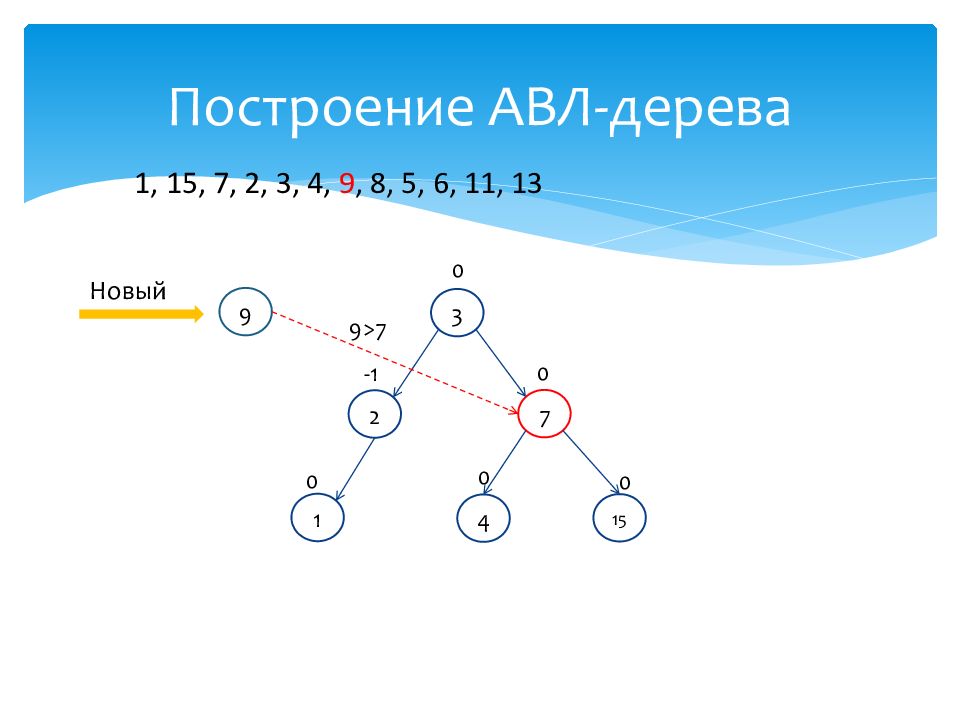
1 0 15 0 7 0 2 -1 3 0 4 0 Новый 9 9>7 1, 15, 7, 2, 3, 4, 9, 8, 5, 6, 11, 13
Слайд 36: Построение АВЛ-дерева
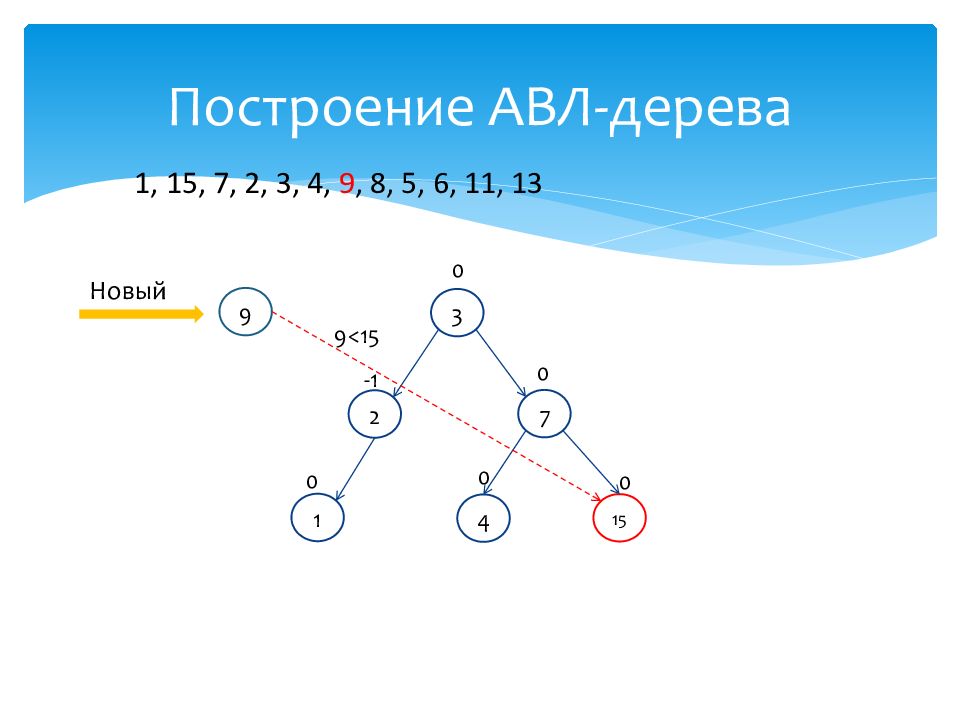
1 0 15 0 7 0 2 -1 3 0 4 0 Новый 9 9<15 1, 15, 7, 2, 3, 4, 9, 8, 5, 6, 11, 13
Слайд 37: Построение АВЛ-дерева
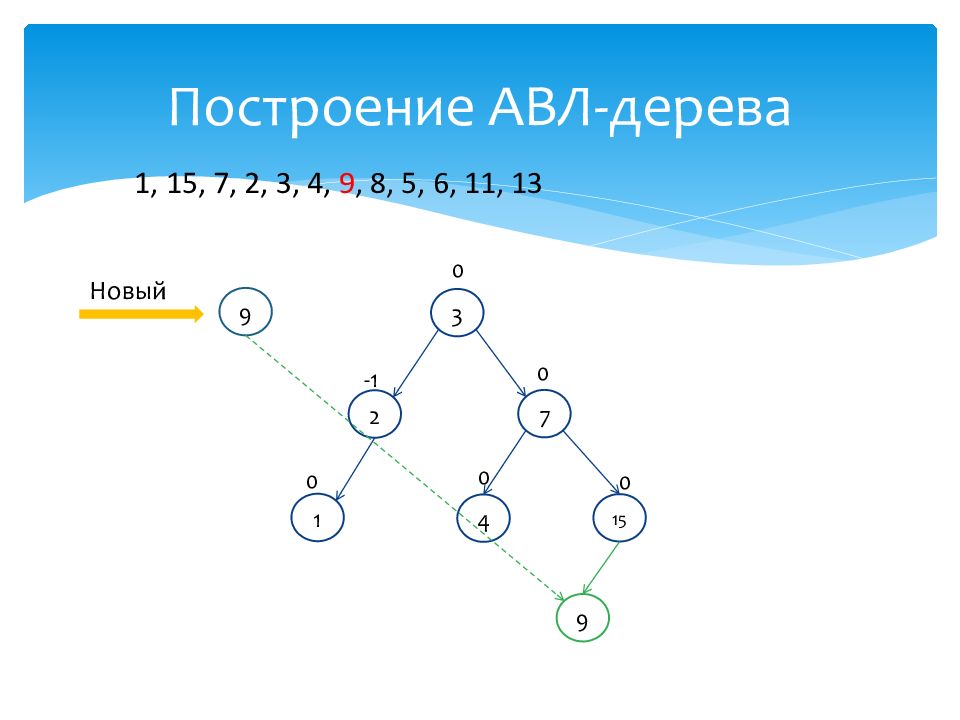
1 0 15 0 7 0 2 -1 3 0 4 0 Новый 9 1, 15, 7, 2, 3, 4, 9, 8, 5, 6, 11, 13 9
Слайд 38: Построение АВЛ-дерева
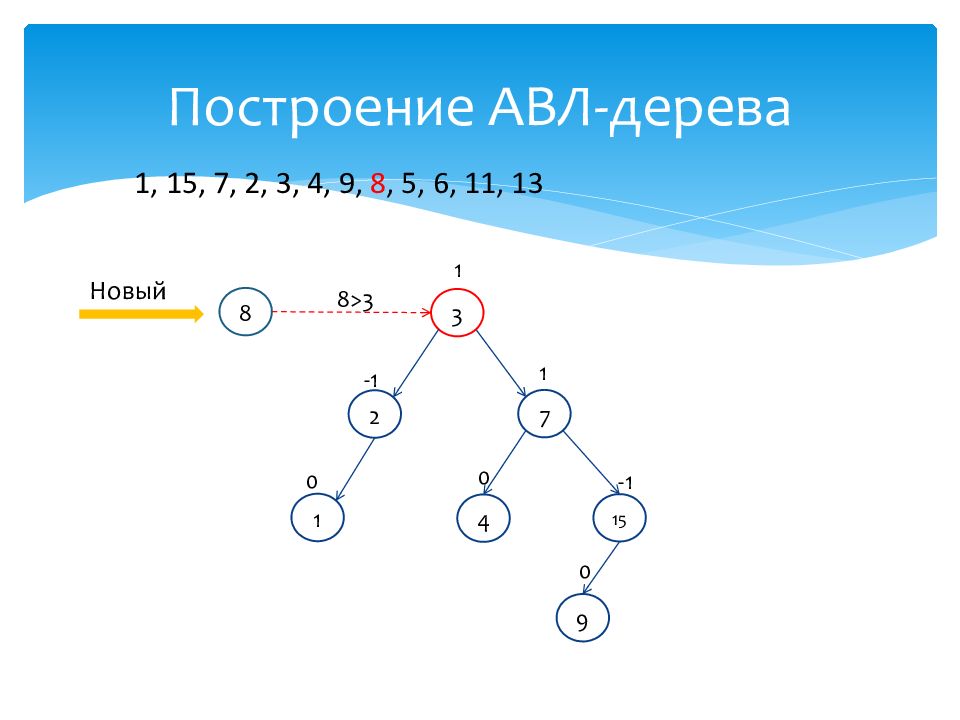
1 0 15 -1 7 1 2 -1 3 1 4 0 Новый 8 1, 15, 7, 2, 3, 4, 9, 8, 5, 6, 11, 13 9 0 8>3
Слайд 39: Построение АВЛ-дерева
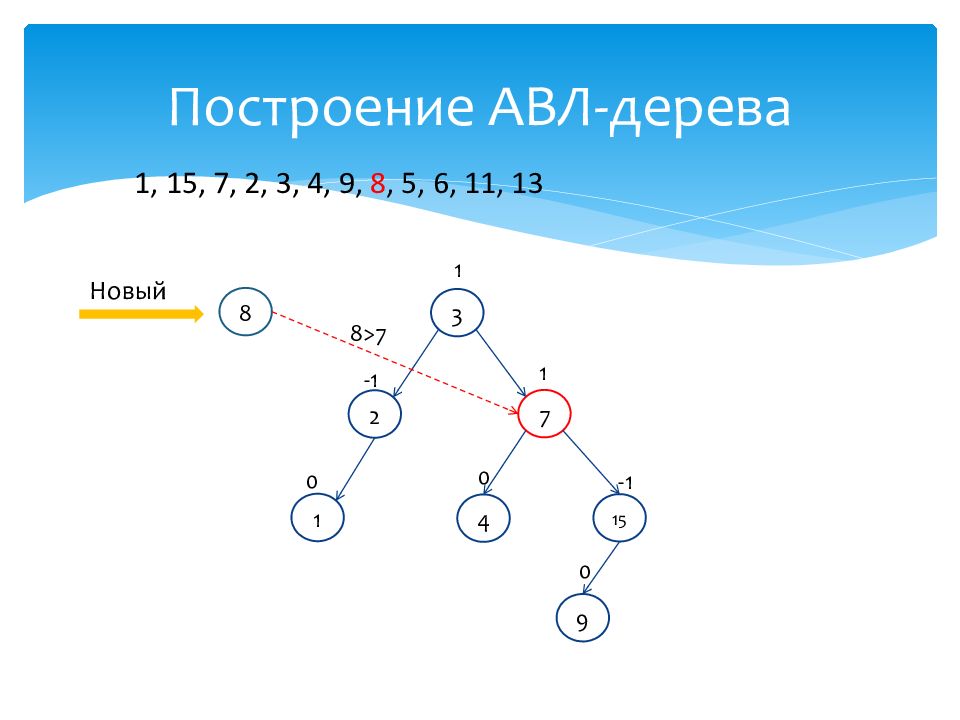
1 0 15 -1 7 1 2 -1 3 1 4 0 Новый 8 1, 15, 7, 2, 3, 4, 9, 8, 5, 6, 11, 13 9 0 8>7
Слайд 40: Построение АВЛ-дерева
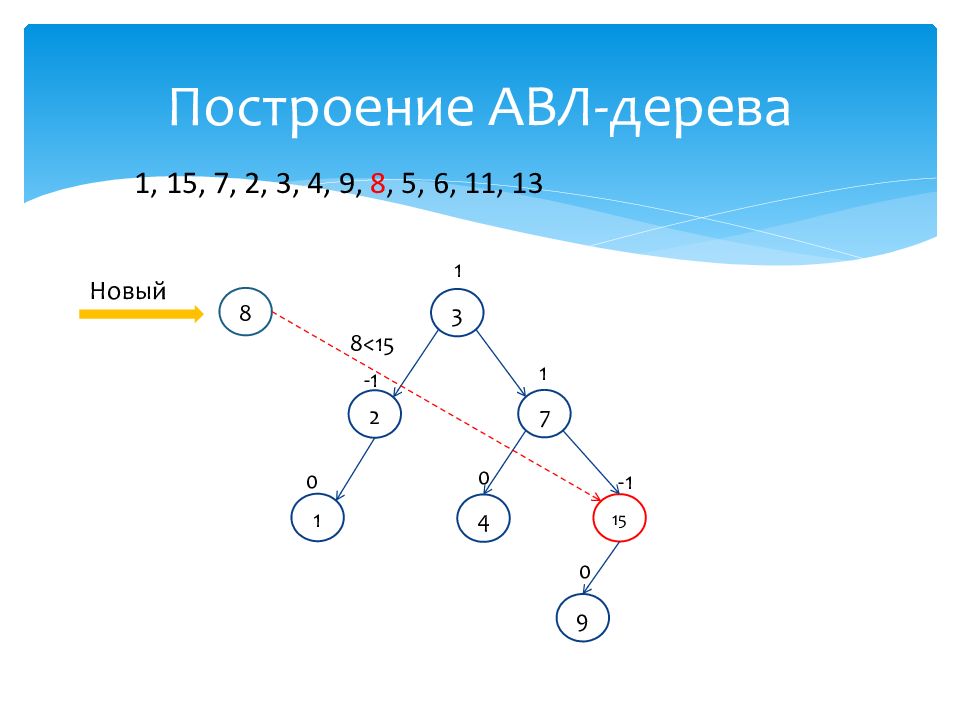
1 0 15 -1 7 1 2 -1 3 1 4 0 Новый 8 1, 15, 7, 2, 3, 4, 9, 8, 5, 6, 11, 13 9 0 8<15
Слайд 41: Построение АВЛ-дерева
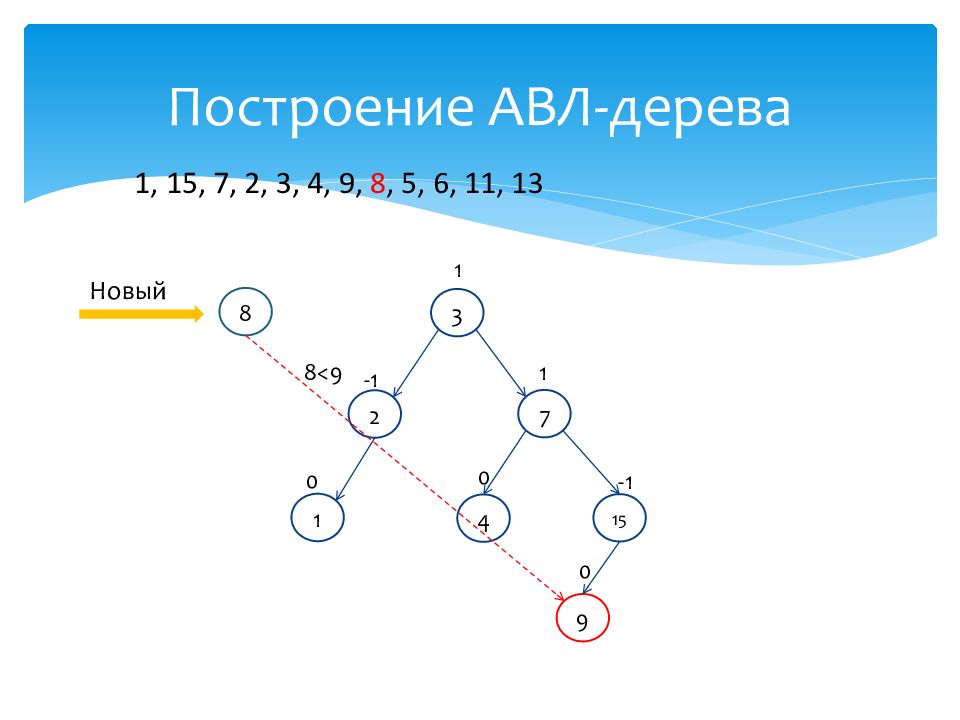
1 0 15 -1 7 1 2 -1 3 1 4 0 Новый 8 1, 15, 7, 2, 3, 4, 9, 8, 5, 6, 11, 13 9 0 8<9
Слайд 42: Построение АВЛ-дерева
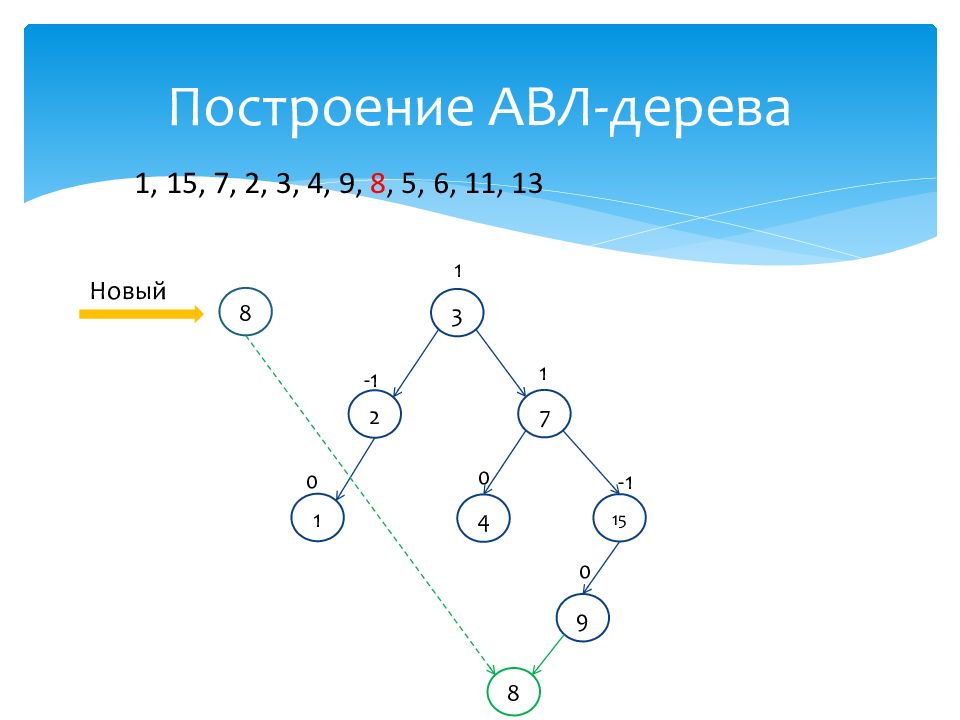
1 0 15 -1 7 1 2 -1 3 1 4 0 Новый 8 1, 15, 7, 2, 3, 4, 9, 8, 5, 6, 11, 13 9 0 8
Слайд 43: Построение АВЛ-дерева
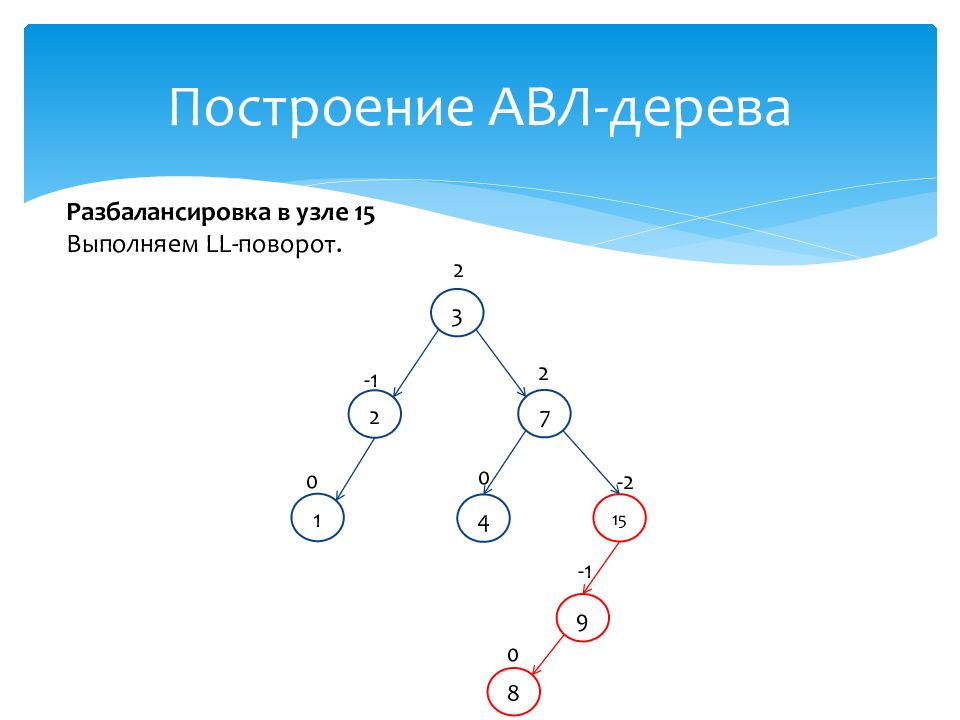
1 0 15 -2 7 2 2 -1 3 2 4 0 9 -1 8 0 Разбалансировка в узле 15 Выполняем LL- поворот.
Слайд 44: Построение АВЛ-дерева
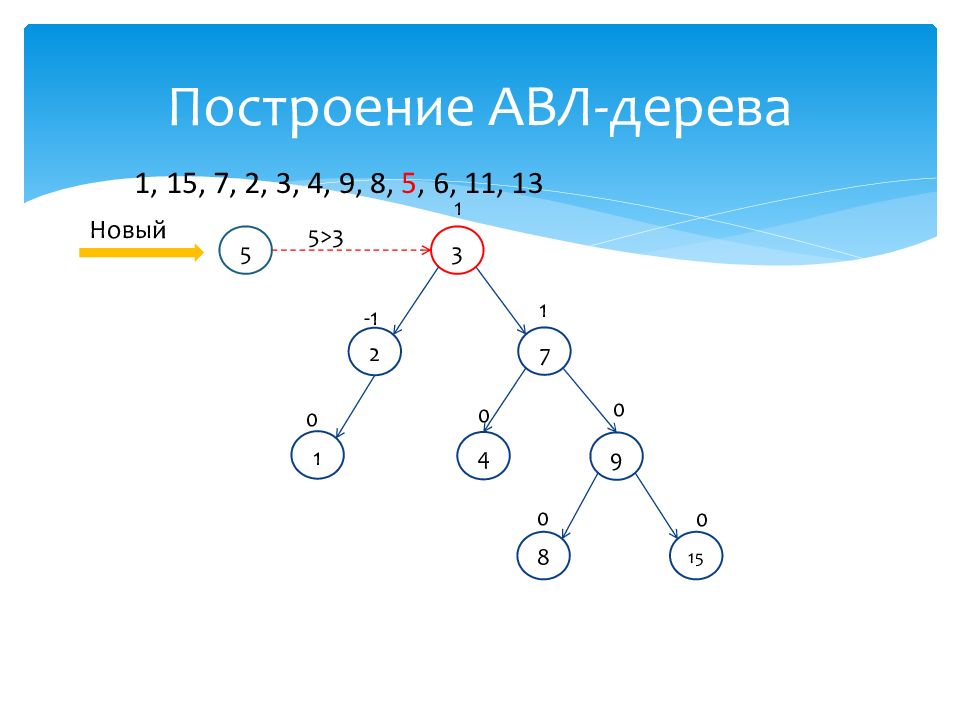
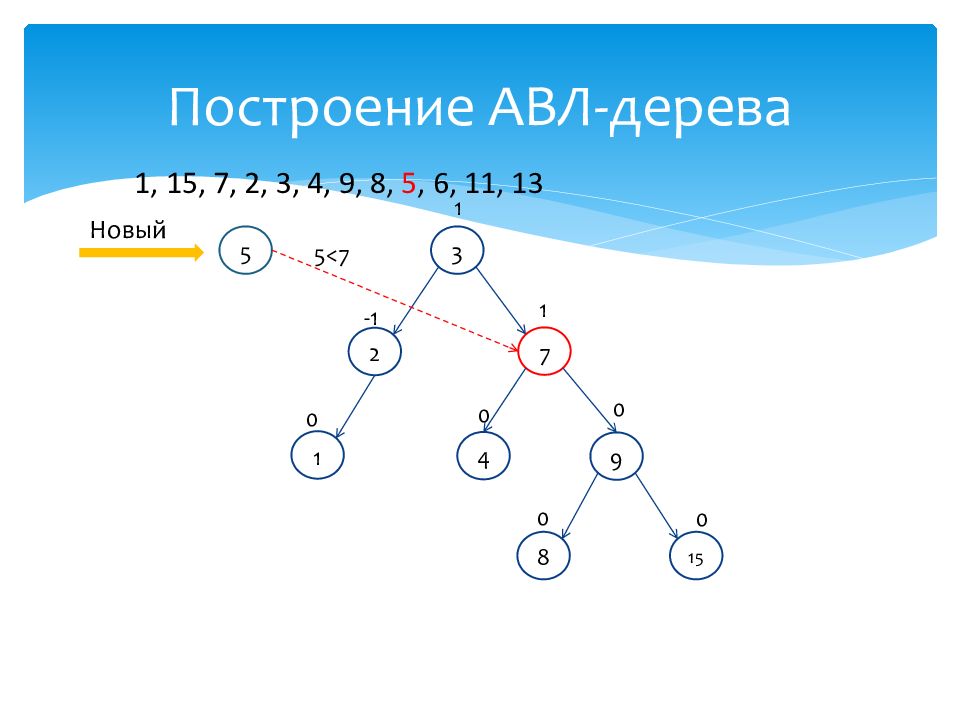
1 0 15 0 7 1 2 -1 3 1 4 0 9 0 8 0 Новый 5 5>3 1, 15, 7, 2, 3, 4, 9, 8, 5, 6, 11, 13
Слайд 45: Построение АВЛ-дерева
1 0 15 0 7 1 2 -1 3 1 4 0 9 0 8 0 Новый 5 5<7 1, 15, 7, 2, 3, 4, 9, 8, 5, 6, 11, 13
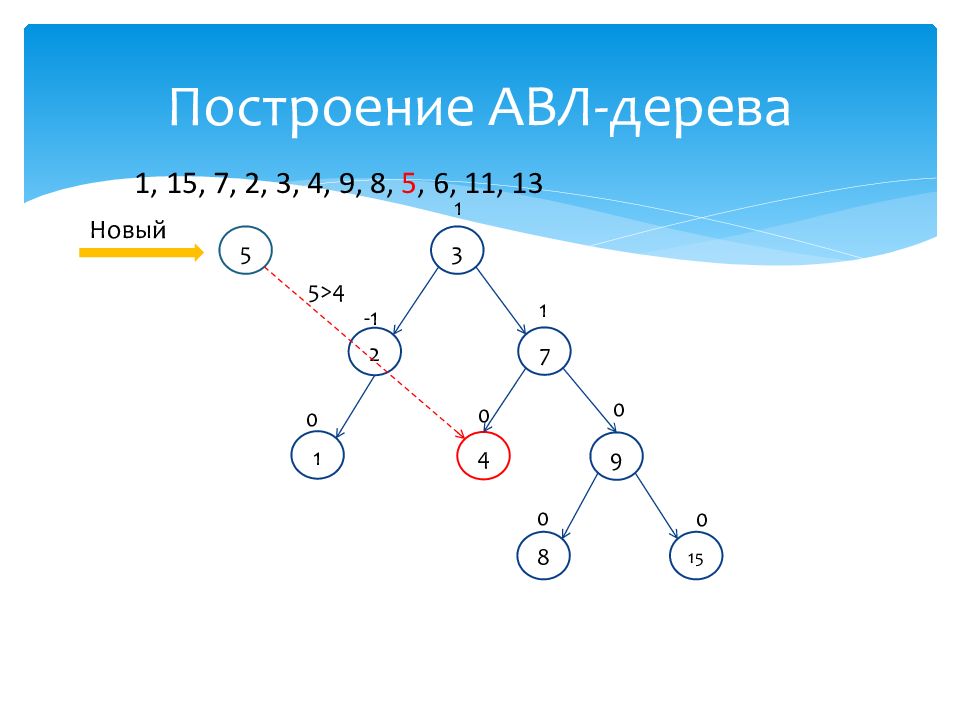
Слайд 46: Построение АВЛ-дерева
1 0 15 0 7 1 2 -1 3 1 4 0 9 0 8 0 Новый 5 5>4 1, 15, 7, 2, 3, 4, 9, 8, 5, 6, 11, 13
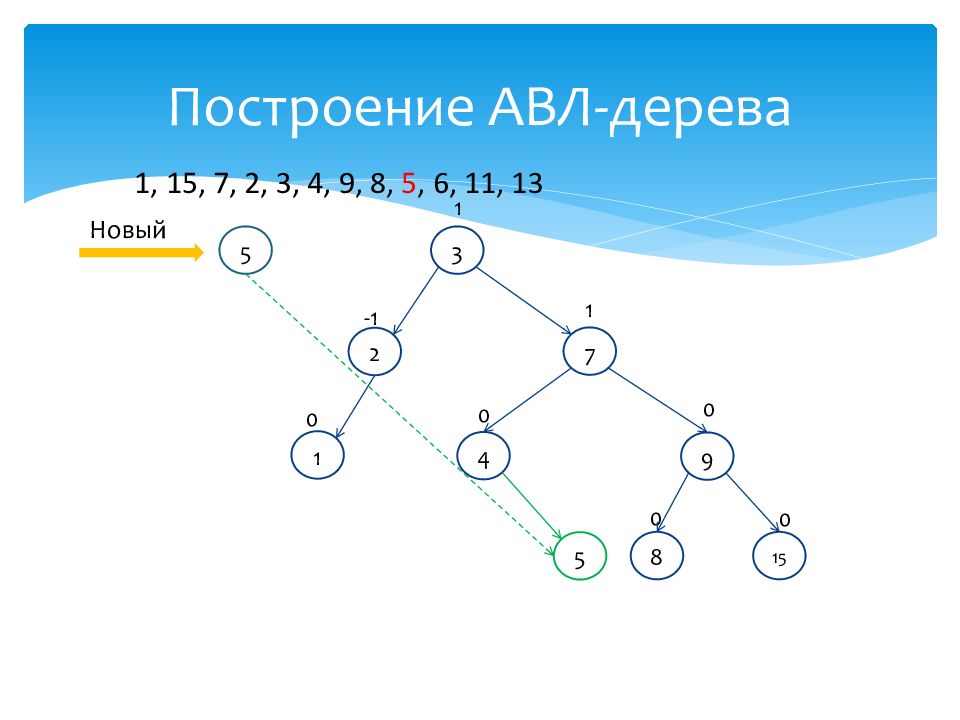
Слайд 47: Построение АВЛ-дерева
1 0 15 0 7 1 2 -1 3 1 4 0 9 0 8 0 Новый 5 1, 15, 7, 2, 3, 4, 9, 8, 5, 6, 11, 13 5
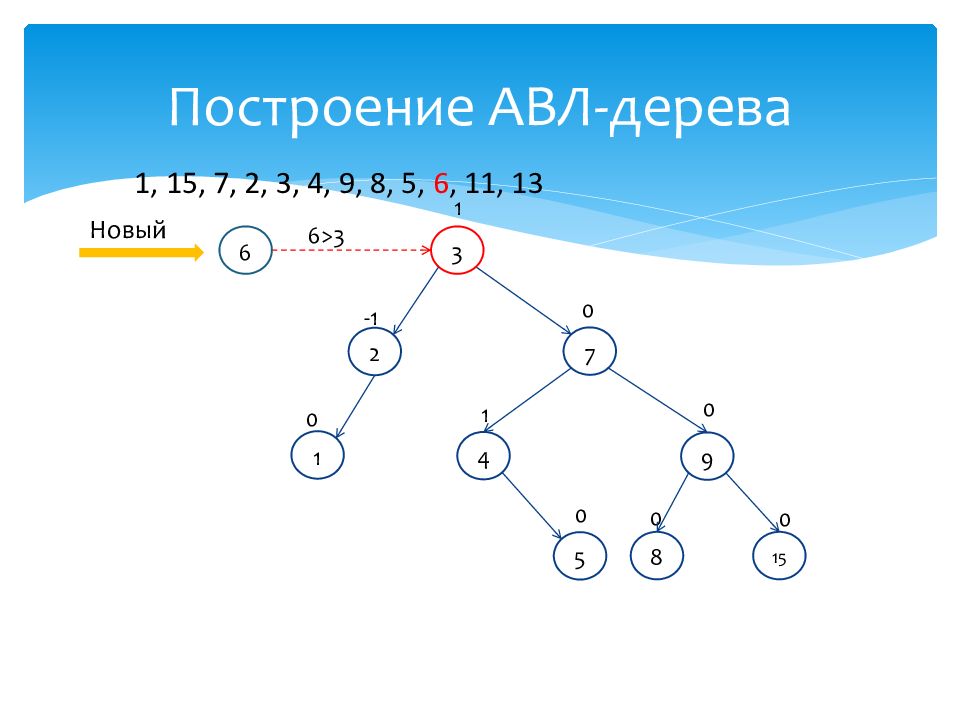
Слайд 48: Построение АВЛ-дерева
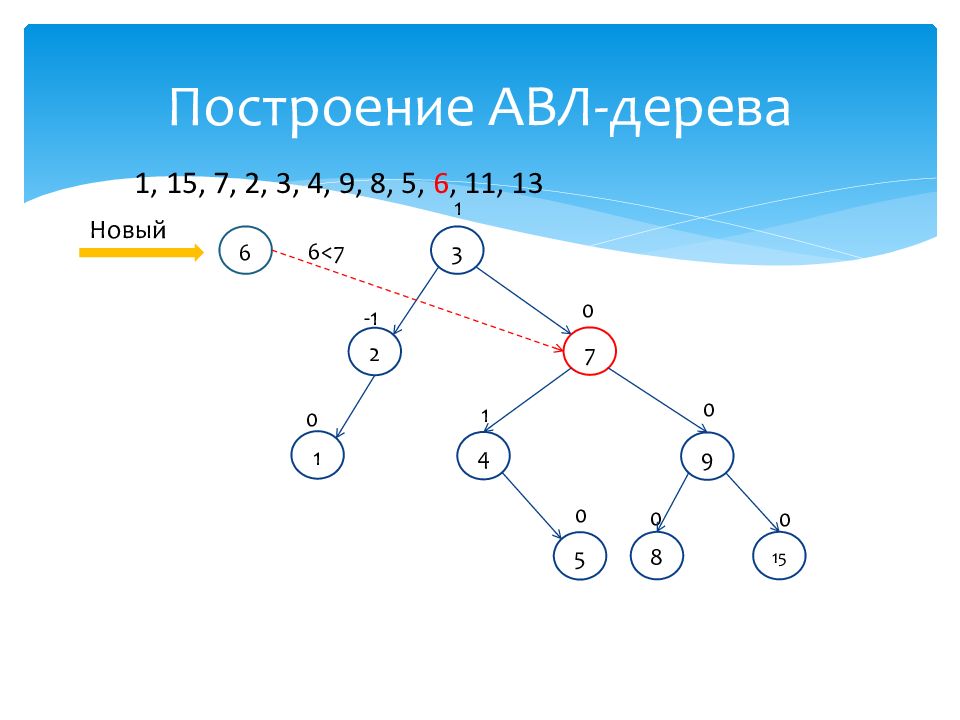
1 0 15 0 7 0 2 -1 3 1 4 1 9 0 8 0 Новый 6 1, 15, 7, 2, 3, 4, 9, 8, 5, 6, 11, 13 5 0 6>3
Слайд 49: Построение АВЛ-дерева
1 0 15 0 7 0 2 -1 3 1 4 1 9 0 8 0 Новый 6 1, 15, 7, 2, 3, 4, 9, 8, 5, 6, 11, 13 5 0 6<7
Слайд 50: Построение АВЛ-дерева
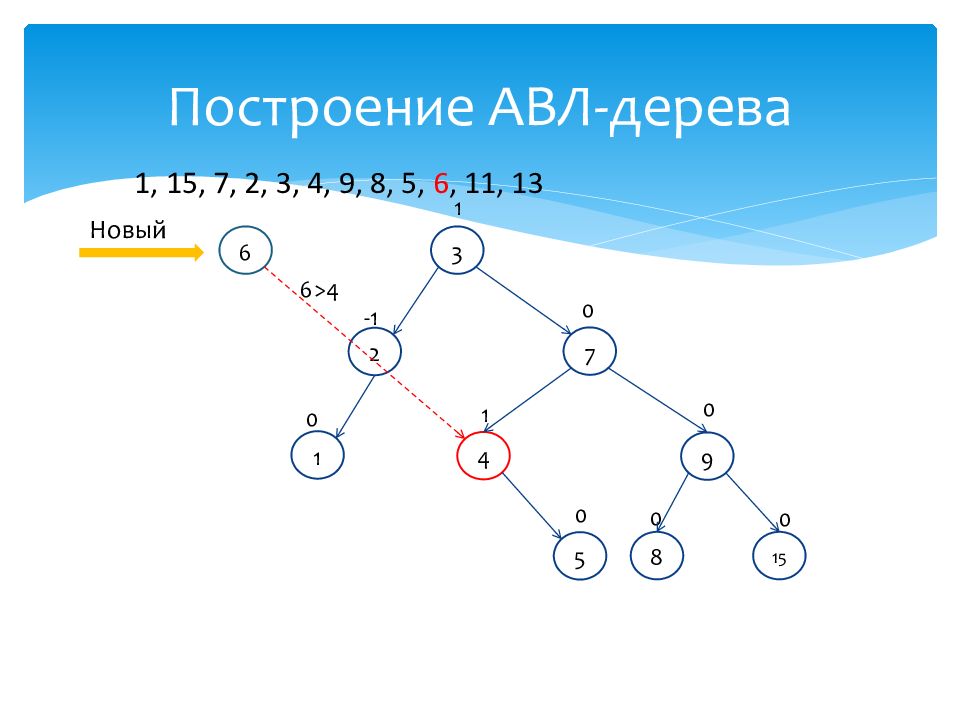
1 0 15 0 7 0 2 -1 3 1 4 1 9 0 8 0 Новый 6 1, 15, 7, 2, 3, 4, 9, 8, 5, 6, 11, 13 5 0 6>4
Слайд 51: Построение АВЛ-дерева
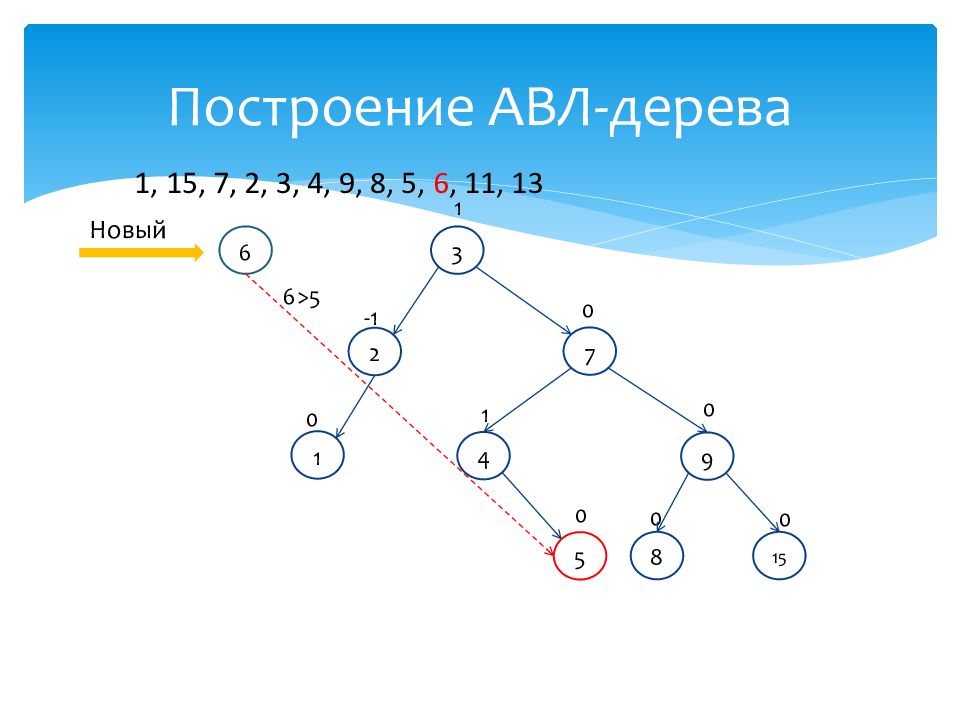
1 0 15 0 7 0 2 -1 3 1 4 1 9 0 8 0 Новый 6 1, 15, 7, 2, 3, 4, 9, 8, 5, 6, 11, 13 5 0 6>5
Слайд 52: Построение АВЛ-дерева
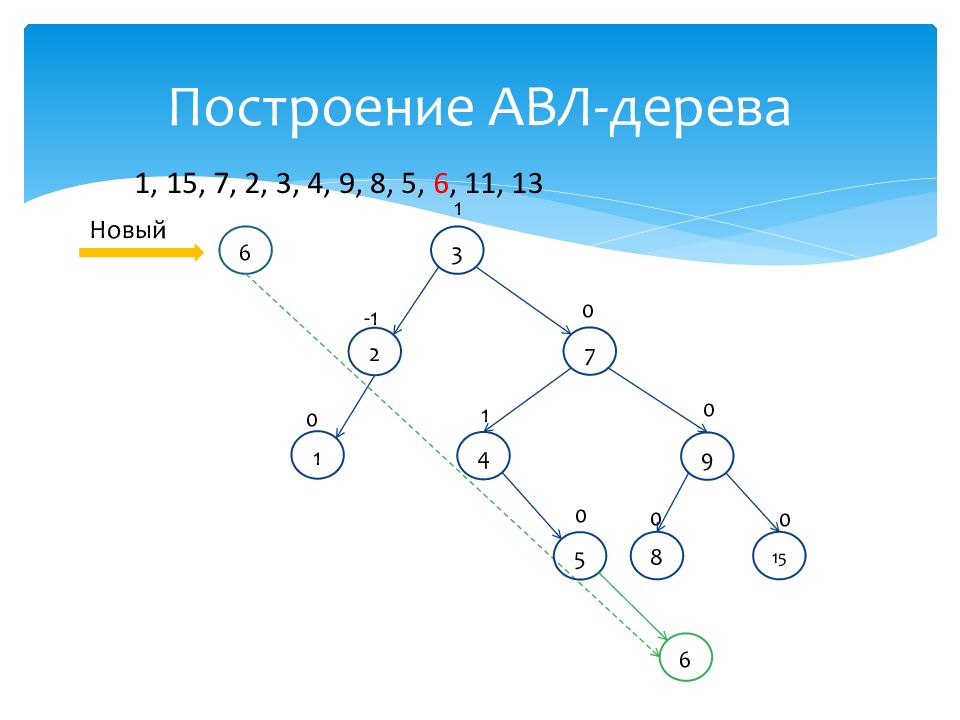
1 0 15 0 7 0 2 -1 3 1 4 1 9 0 8 0 Новый 6 1, 15, 7, 2, 3, 4, 9, 8, 5, 6, 11, 13 5 0 6
Слайд 53: Построение АВЛ-дерева
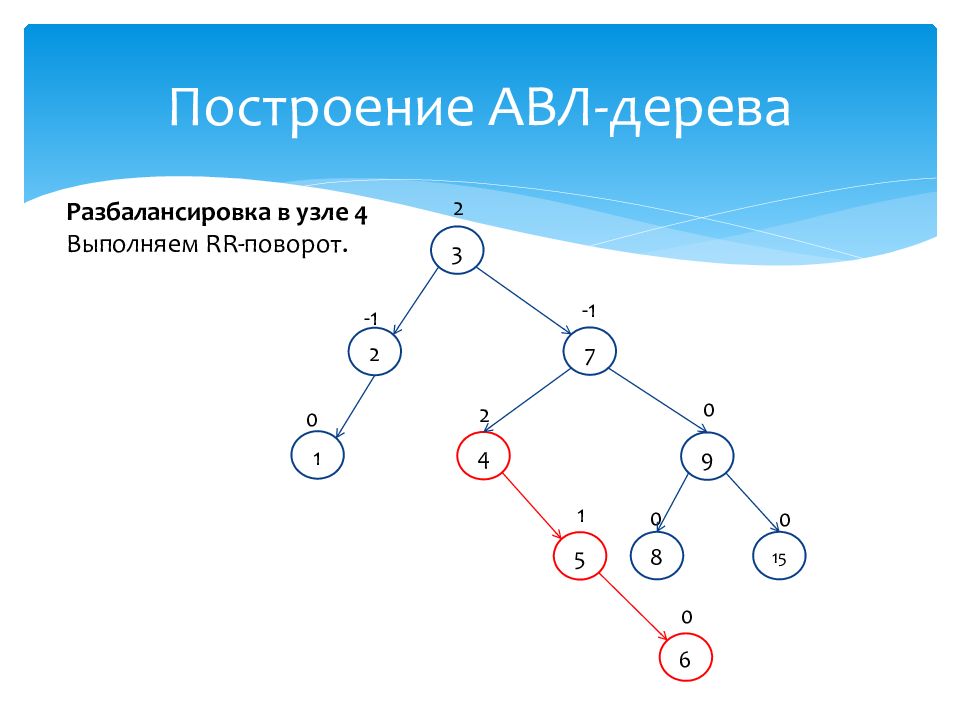
1 0 15 0 7 -1 2 -1 3 2 4 2 9 0 8 0 5 1 6 0 Разбалансировка в узле 4 Выполняем RR- поворот.
Слайд 54: Построение АВЛ-дерева
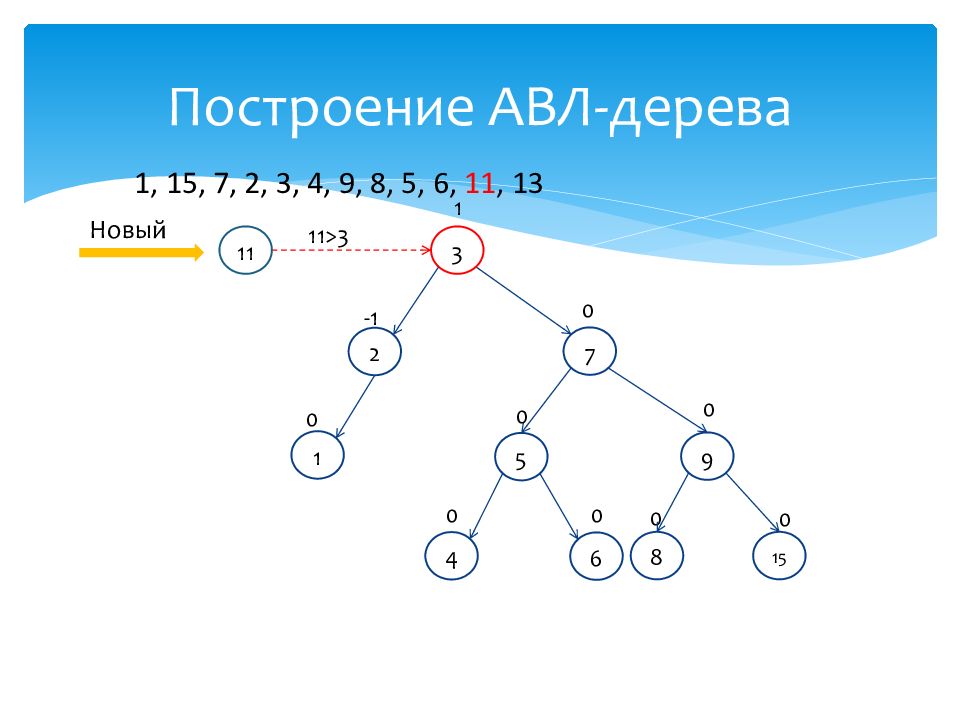
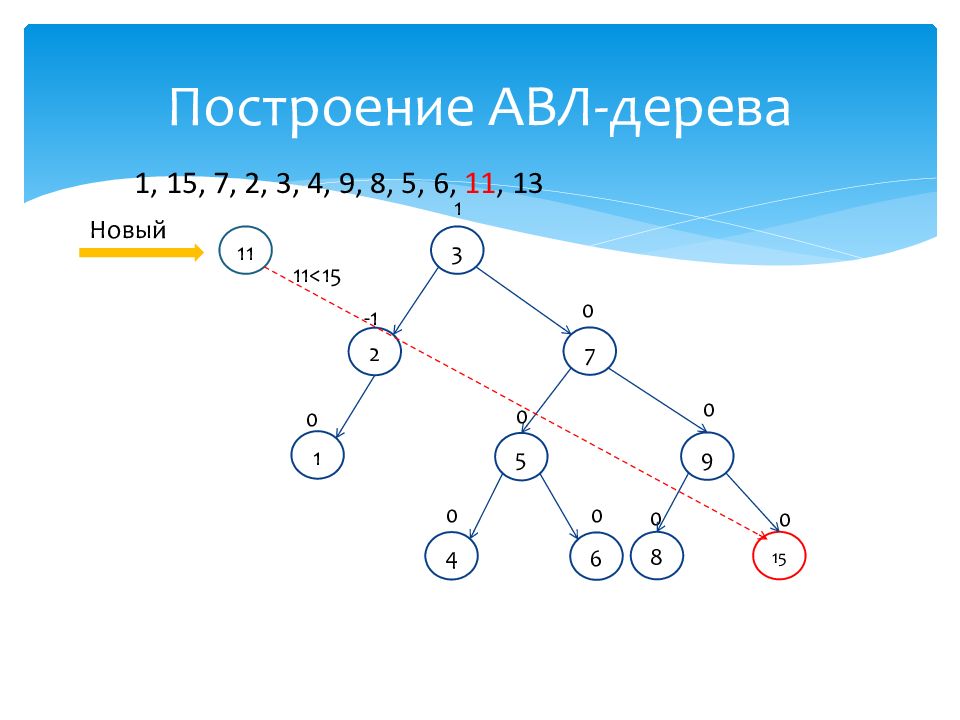
1 0 15 0 7 0 2 -1 3 1 4 0 9 0 8 0 5 0 6 0 Новый 11 11>3 1, 15, 7, 2, 3, 4, 9, 8, 5, 6, 11, 13
Слайд 55: Построение АВЛ-дерева
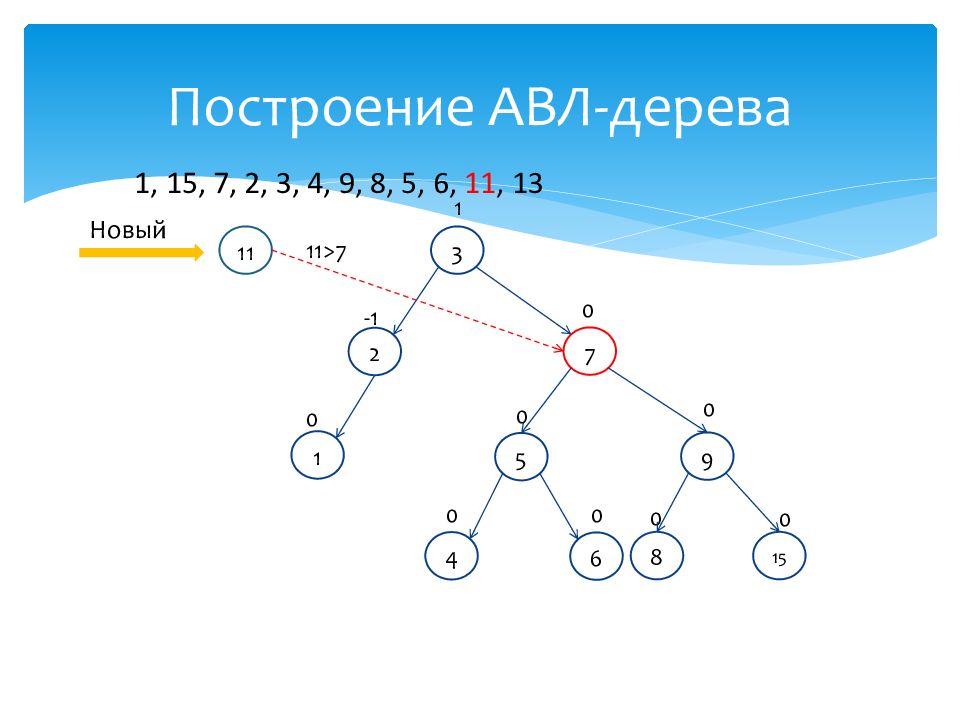
1 0 15 0 7 0 2 -1 3 1 4 0 9 0 8 0 5 0 6 0 Новый 11 11>7 1, 15, 7, 2, 3, 4, 9, 8, 5, 6, 11, 13
Слайд 56: Построение АВЛ-дерева
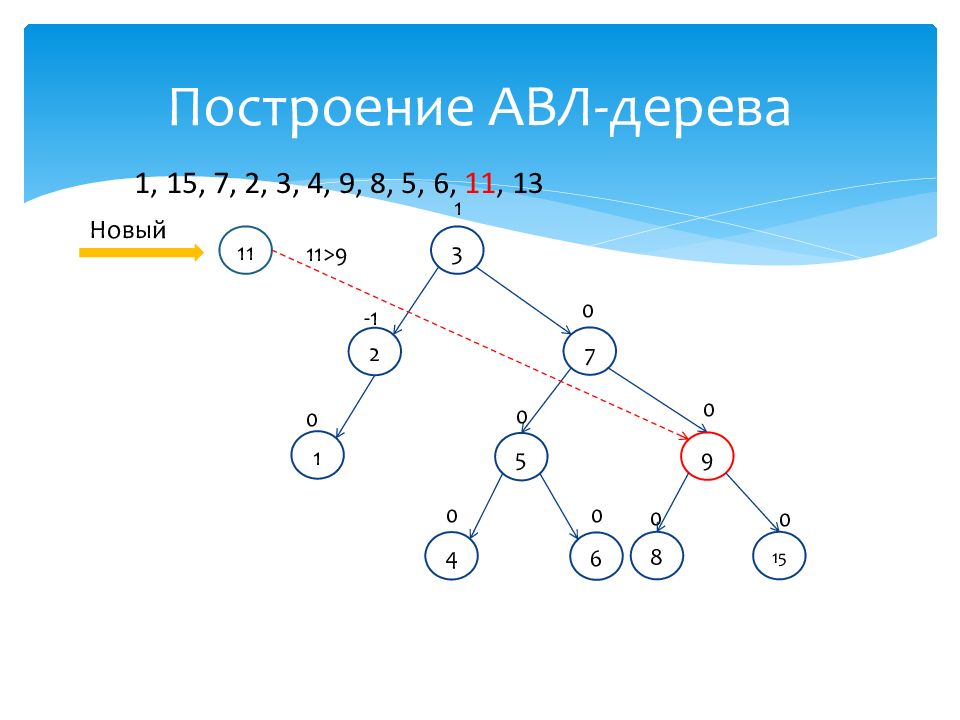
1 0 15 0 7 0 2 -1 3 1 4 0 9 0 8 0 5 0 6 0 Новый 11 11>9 1, 15, 7, 2, 3, 4, 9, 8, 5, 6, 11, 13
Слайд 57: Построение АВЛ-дерева
1 0 15 0 7 0 2 -1 3 1 4 0 9 0 8 0 5 0 6 0 Новый 11 11<15 1, 15, 7, 2, 3, 4, 9, 8, 5, 6, 11, 13
Слайд 58: Построение АВЛ-дерева
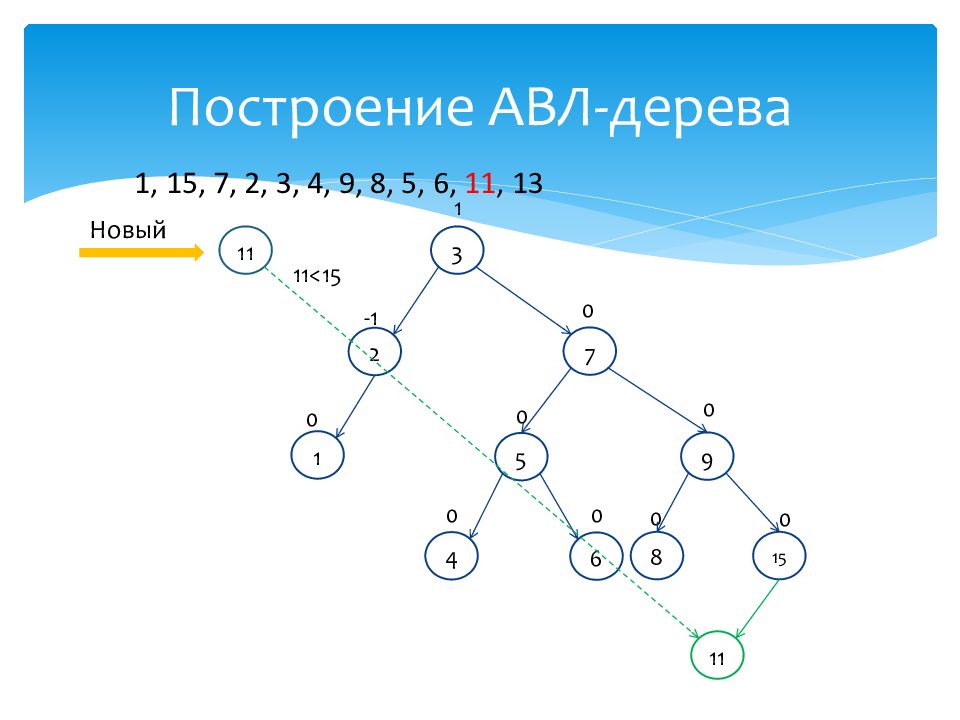
1 0 15 0 7 0 2 -1 3 1 4 0 9 0 8 0 5 0 6 0 Новый 11 11<15 1, 15, 7, 2, 3, 4, 9, 8, 5, 6, 11, 13 11
Слайд 59: Построение АВЛ-дерева
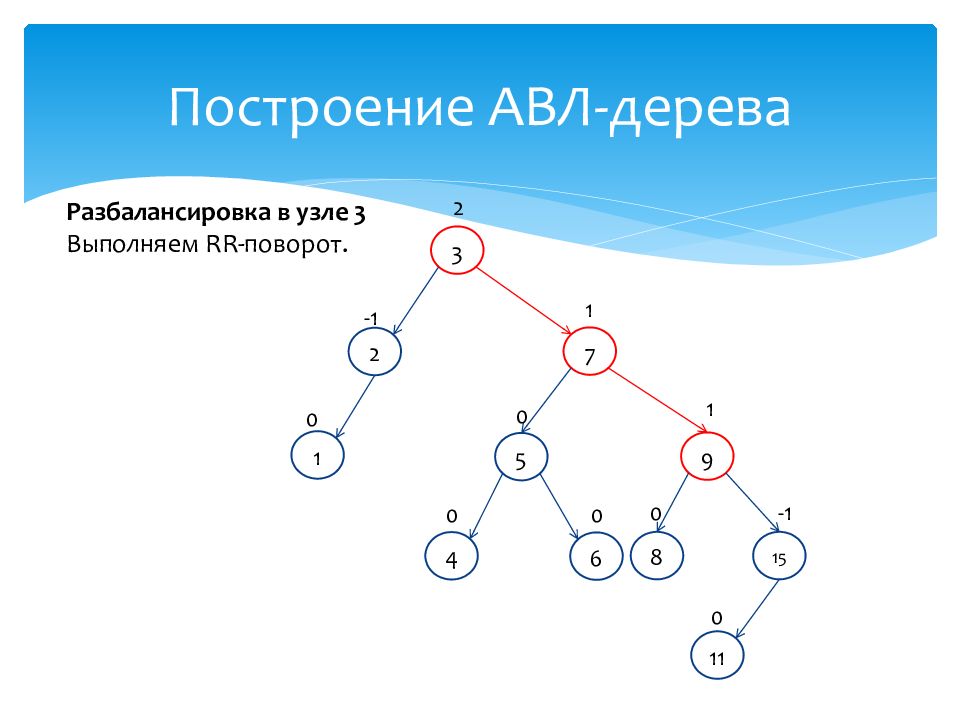
1 0 15 -1 7 1 2 -1 3 2 4 0 9 1 8 0 5 0 6 0 11 0 Разбалансировка в узле 3 Выполняем RR- поворот.
Слайд 60: Построение АВЛ-дерева
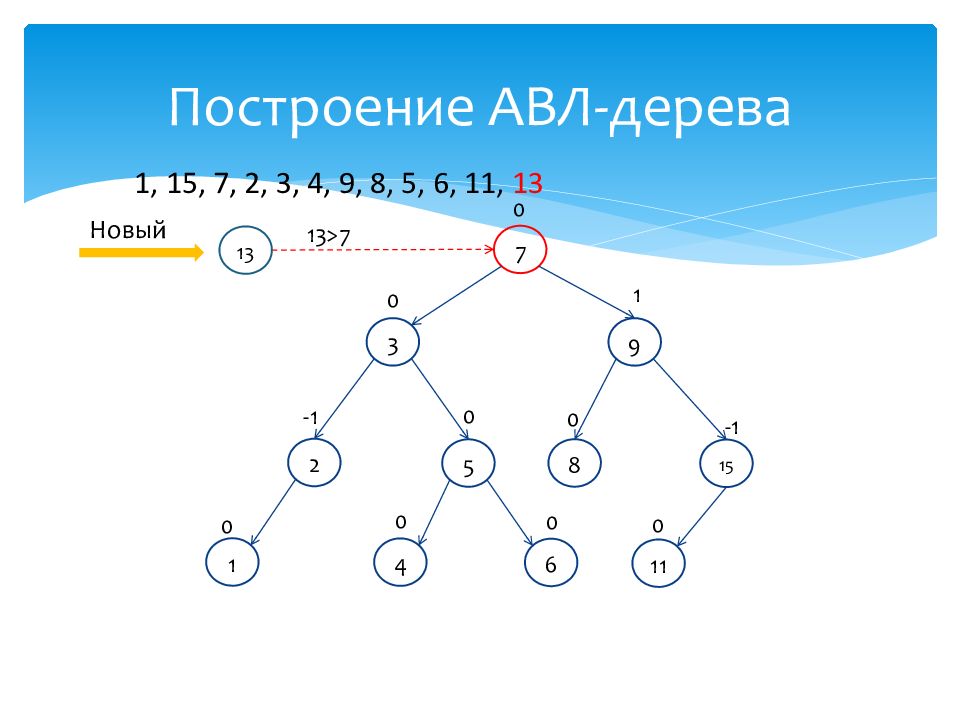
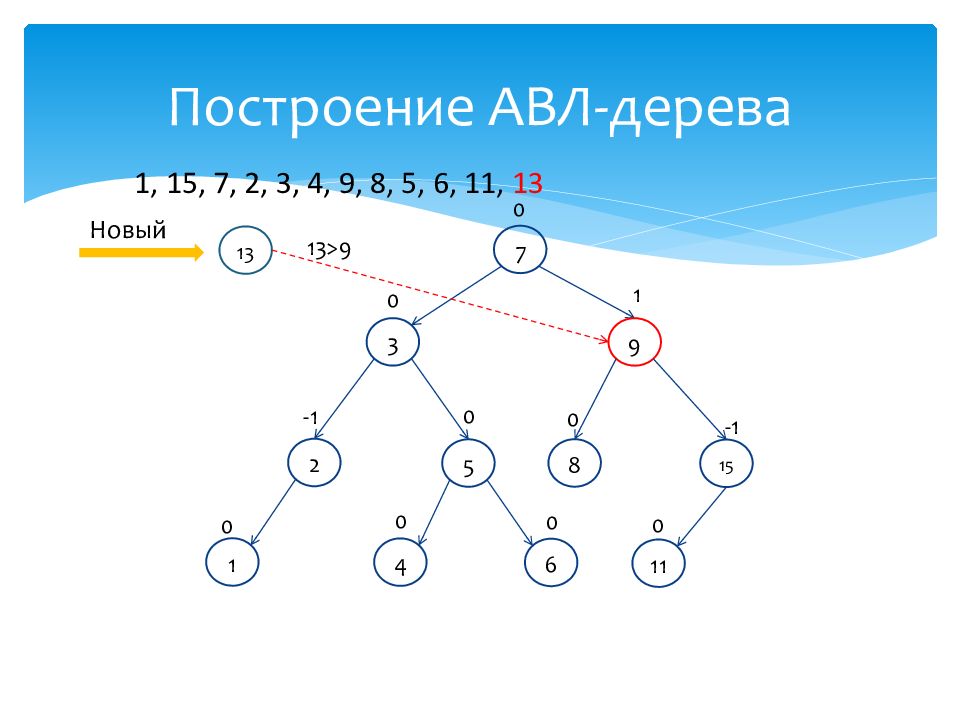
1 0 15 -1 7 0 2 -1 3 0 4 0 9 1 8 0 5 0 6 0 11 0 1, 15, 7, 2, 3, 4, 9, 8, 5, 6, 11, 13 Новый 13 13>7
Слайд 61: Построение АВЛ-дерева
1 0 15 -1 7 0 2 -1 3 0 4 0 9 1 8 0 5 0 6 0 11 0 1, 15, 7, 2, 3, 4, 9, 8, 5, 6, 11, 13 Новый 13 13>9
Слайд 62: Построение АВЛ-дерева
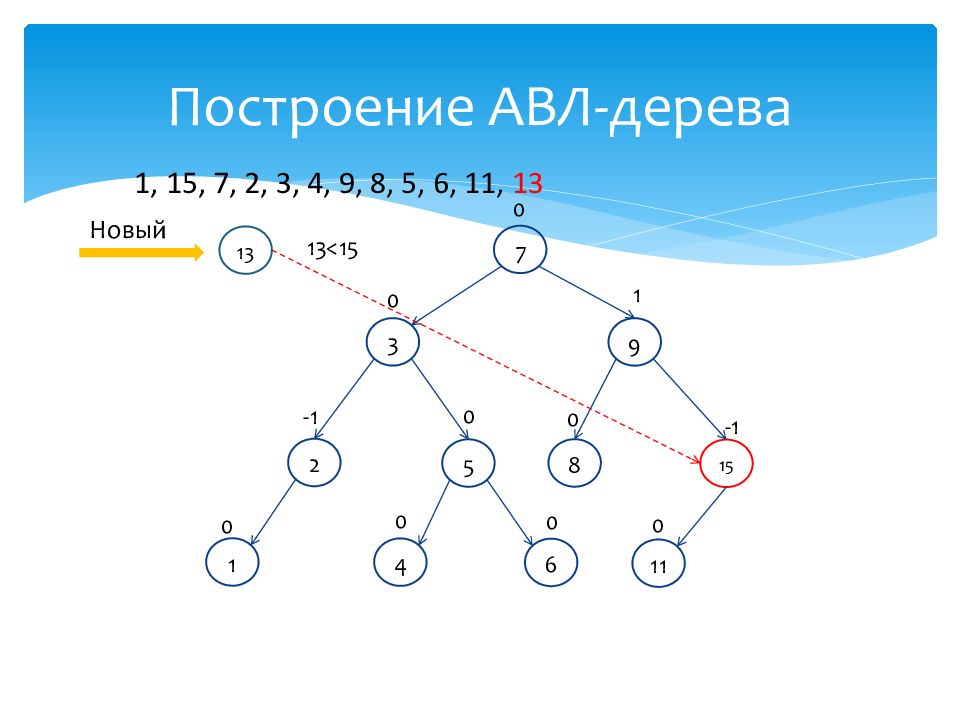
1 0 15 -1 7 0 2 -1 3 0 4 0 9 1 8 0 5 0 6 0 11 0 1, 15, 7, 2, 3, 4, 9, 8, 5, 6, 11, 13 Новый 13 13<15
Слайд 63: Построение АВЛ-дерева
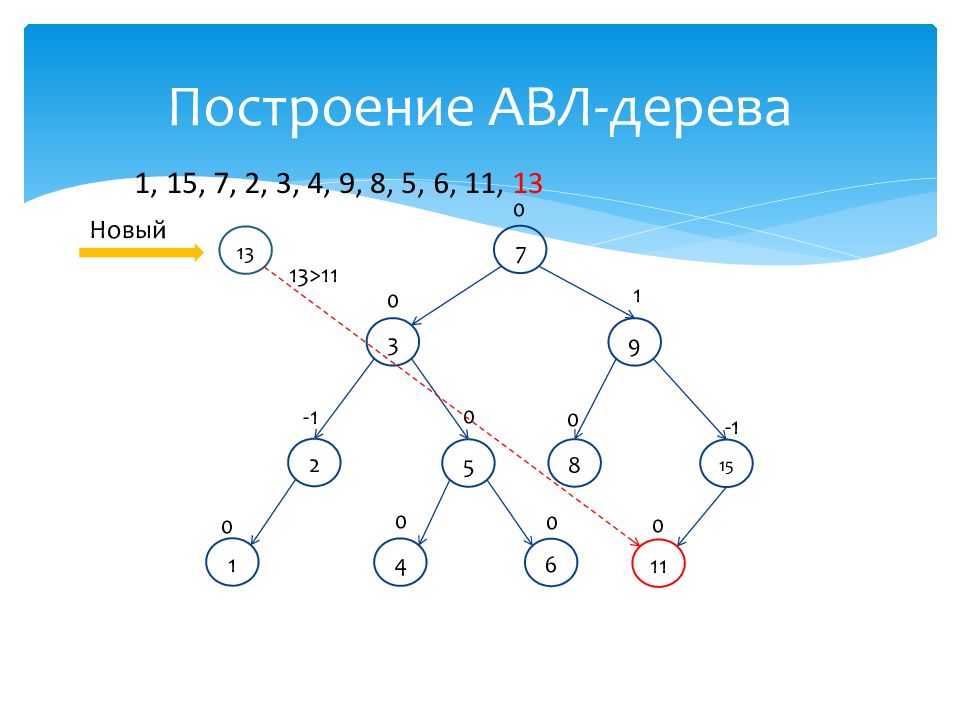
1 0 15 -1 7 0 2 -1 3 0 4 0 9 1 8 0 5 0 6 0 11 0 1, 15, 7, 2, 3, 4, 9, 8, 5, 6, 11, 13 Новый 13 13>11
Слайд 64: Построение АВЛ-дерева
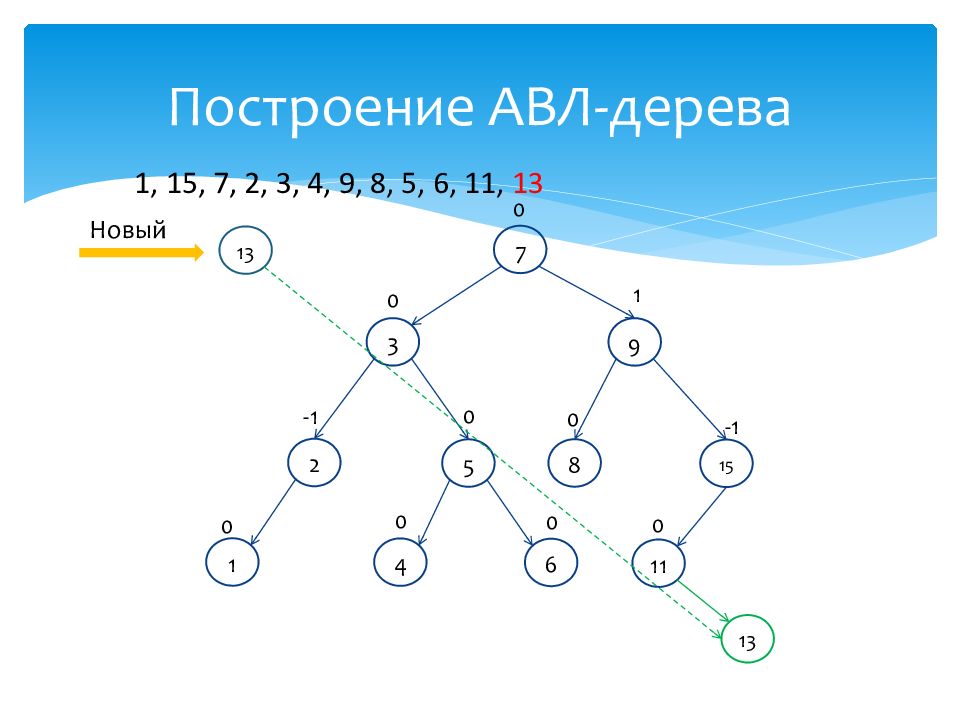
1 0 15 -1 7 0 2 -1 3 0 4 0 9 1 8 0 5 0 6 0 11 0 1, 15, 7, 2, 3, 4, 9, 8, 5, 6, 11, 13 Новый 13 13
Слайд 65: Построение АВЛ-дерева
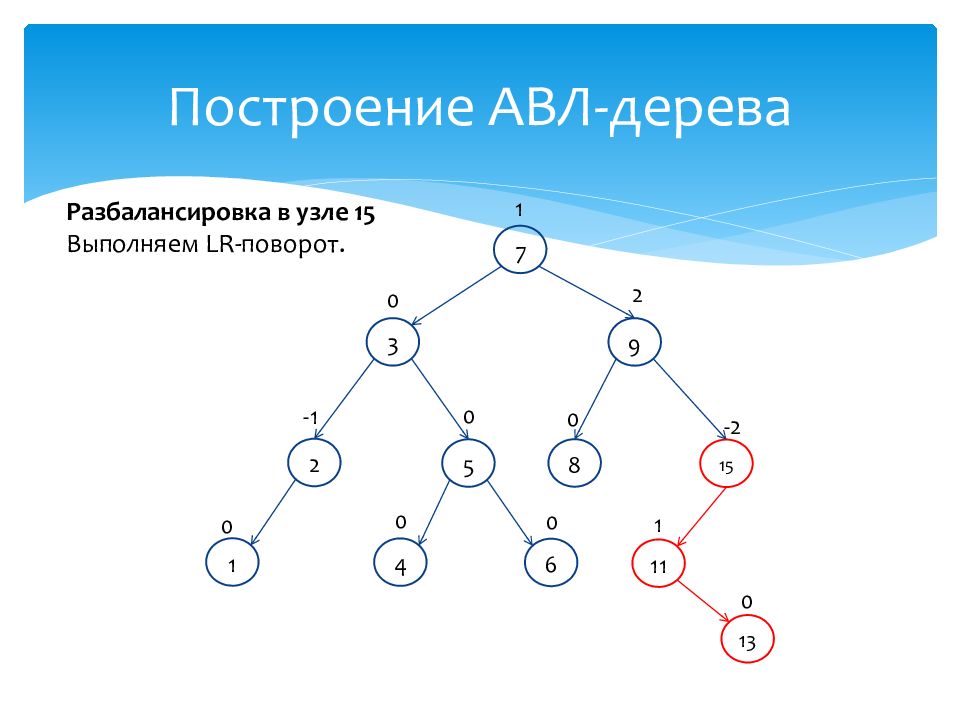
1 0 15 -2 7 1 2 -1 3 0 4 0 9 2 8 0 5 0 6 0 11 1 13 0 Разбалансировка в узле 15 Выполняем L R- поворот.
Слайд 66: Построение АВЛ-дерева
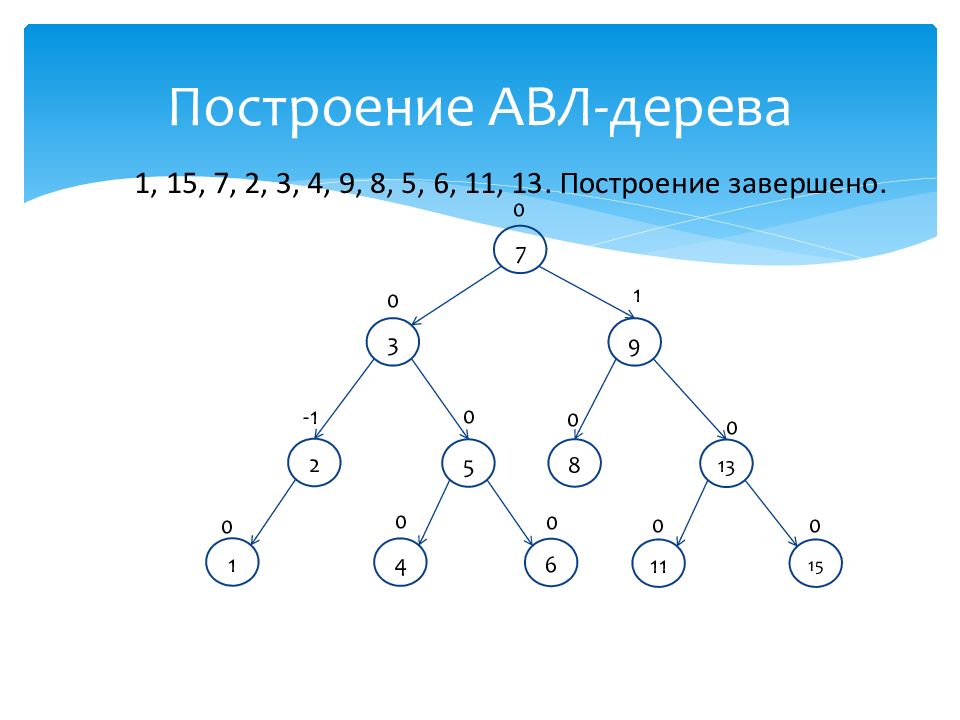
1 0 13 0 7 0 2 -1 3 0 4 0 9 1 8 0 5 0 6 0 11 0 15 0 1, 15, 7, 2, 3, 4, 9, 8, 5, 6, 11, 13. Построение завершено.
Слайд 67: Удаление узла из АВЛ-дерева
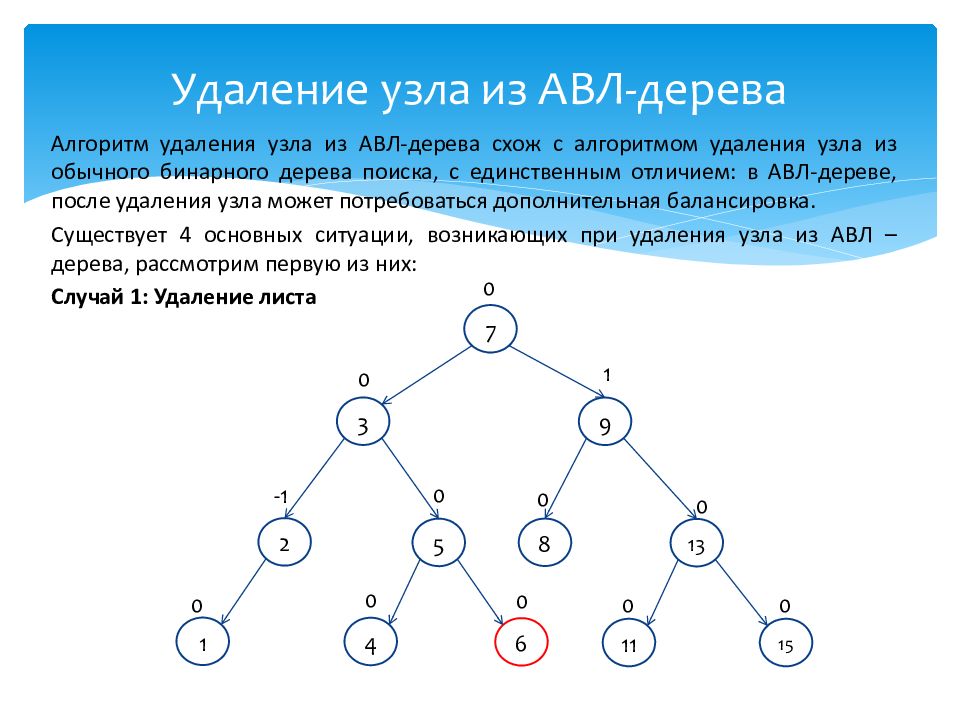
Алгоритм удаления узла из АВЛ-дерева схож с алгоритмом удаления узла из обычного бинарного дерева поиска, с единственным отличием: в АВЛ-дереве, после удаления узла может потребоваться дополнительная балансировка. Существует 4 основных ситуации, возникающих при удаления узла из АВЛ – дерева, рассмотрим первую из них: Случай 1: Удаление листа 1 0 13 0 7 0 2 -1 3 0 4 0 9 1 8 0 5 0 6 0 11 0 15 0 Удаление узла из АВЛ-дерева
Слайд 68: Удаление узла из АВЛ-дерева (случай 1)
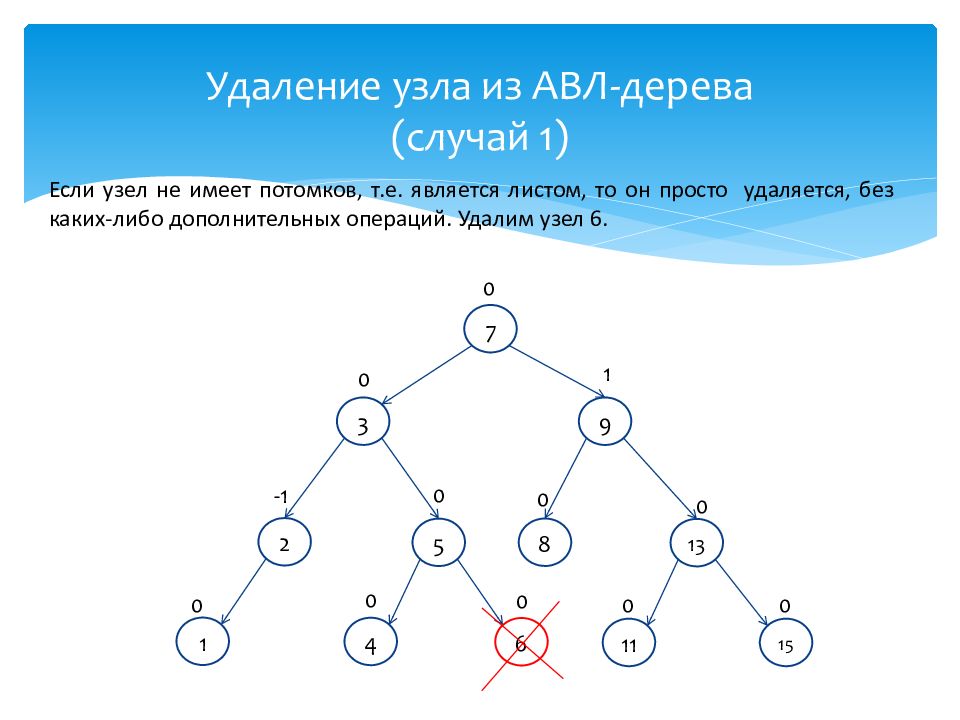
Если узел не имеет потомков, т.е. является листом, то он просто удаляется, без каких-либо дополнительных операций. Удалим узел 6. 1 0 13 0 7 0 2 -1 3 0 4 0 9 1 8 0 5 0 6 0 11 0 15 0
Слайд 69: Удаление узла из АВЛ-дерева (случай 2)
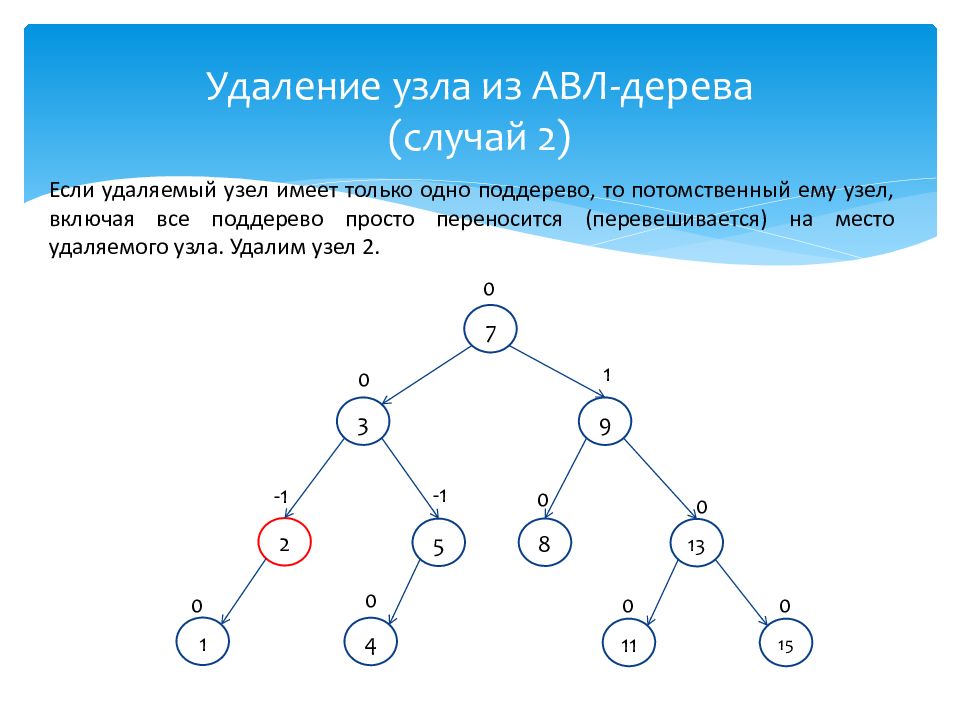
Если удаляемый узел имеет только одно поддерево, то потомственный ему узел, включая все поддерево просто переносится (перевешивается) на место удаляемого узла. Удалим узел 2. 1 0 13 0 7 0 2 -1 3 0 4 0 9 1 8 0 5 -1 11 0 15 0
Слайд 70: Удаление узла из АВЛ-дерева (случай 2)
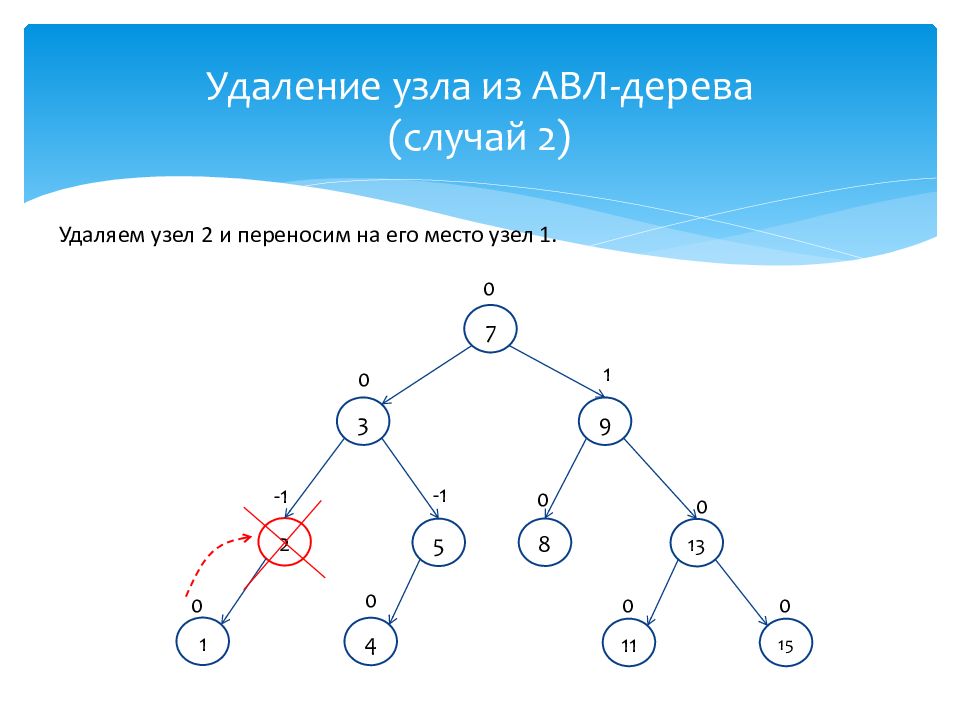
Удаляем узел 2 и переносим на его место узел 1. 1 0 13 0 7 0 2 -1 3 0 4 0 9 1 8 0 5 -1 11 0 15 0
Слайд 71: Удаление узла из АВЛ-дерева (случай 3)
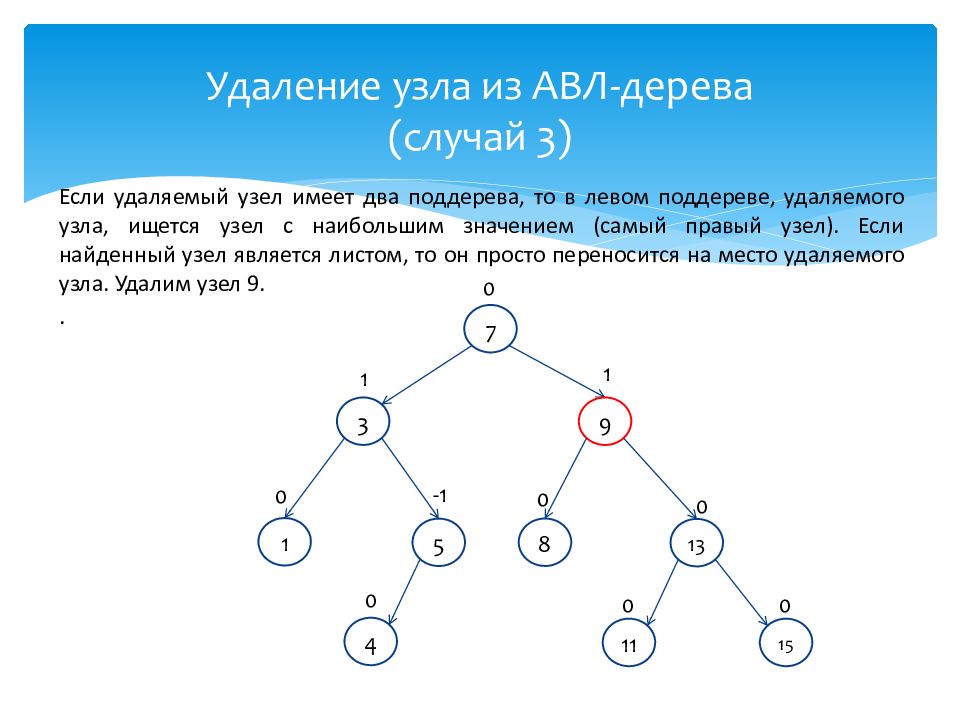
Если удаляемый узел имеет два поддерева, то в левом поддереве, удаляемого узла, ищется узел с наибольшим значением (самый правый узел). Если найденный узел является листом, то он просто переносится на место удаляемого узла. Удалим узел 9. . 13 0 7 0 1 0 3 1 4 0 9 1 8 0 5 -1 11 0 15 0
Слайд 72: Удаление узла из АВЛ-дерева (случай 3)
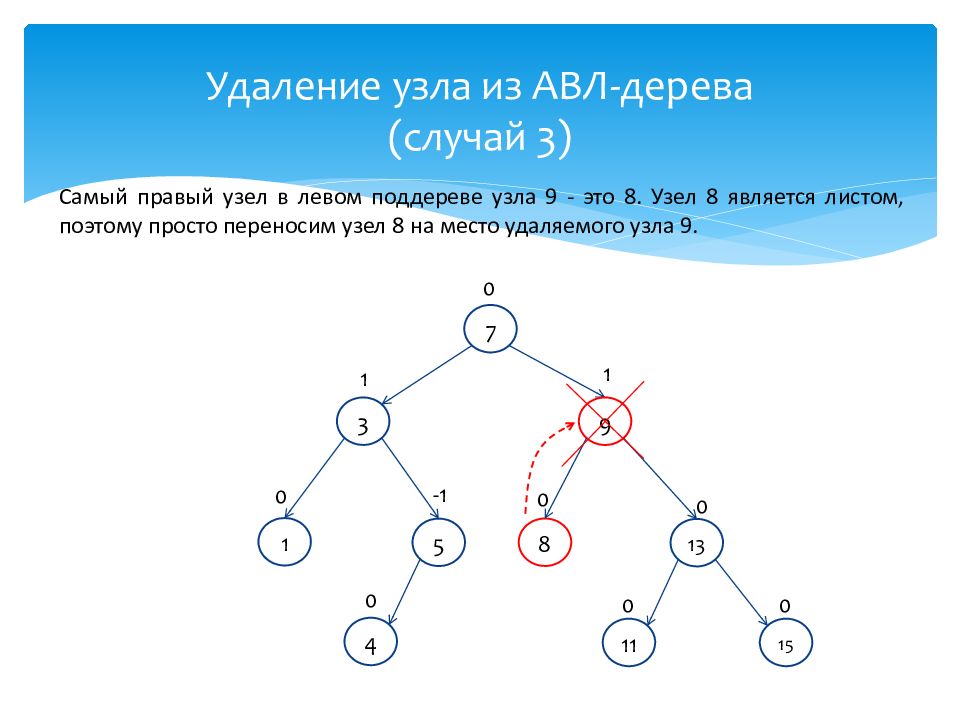
С амый правый узел в левом поддереве узла 9 - это 8. Узел 8 является листом, поэтому просто переносим узел 8 на место удаляемого узла 9. 13 0 7 0 1 0 3 1 4 0 9 1 8 0 5 -1 11 0 15 0
Слайд 73: Удаление узла из АВЛ-дерева (случай 3)
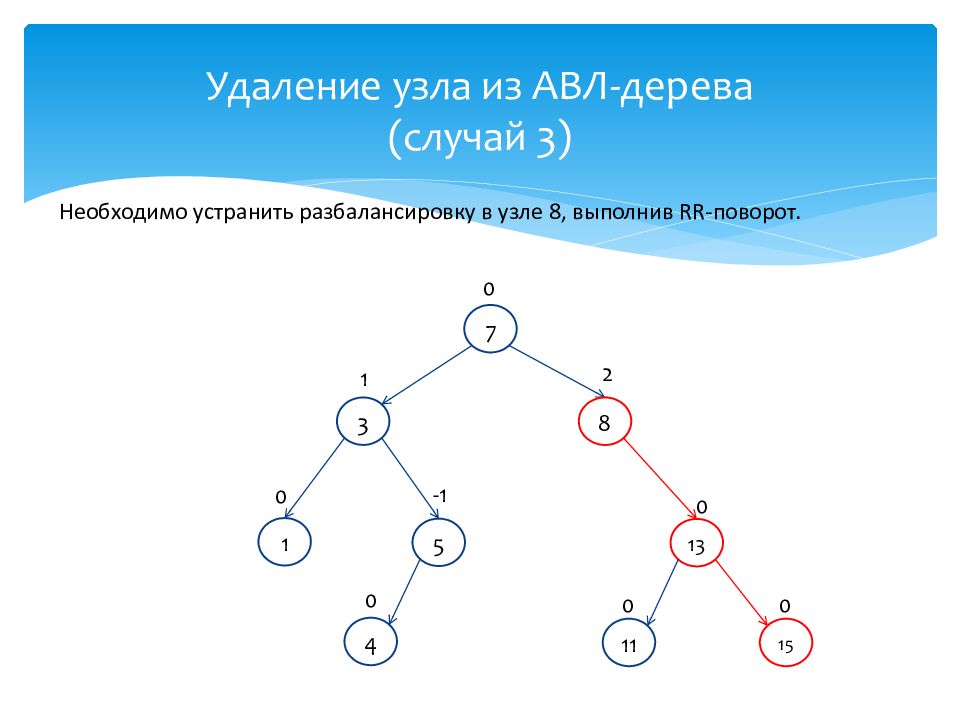
Необходимо устранить разбалансировку в узле 8, выполнив RR- поворот. 13 0 7 0 1 0 3 1 4 0 8 2 5 -1 11 0 15 0
Слайд 74: Удаление узла из АВЛ-дерева (случай 4)
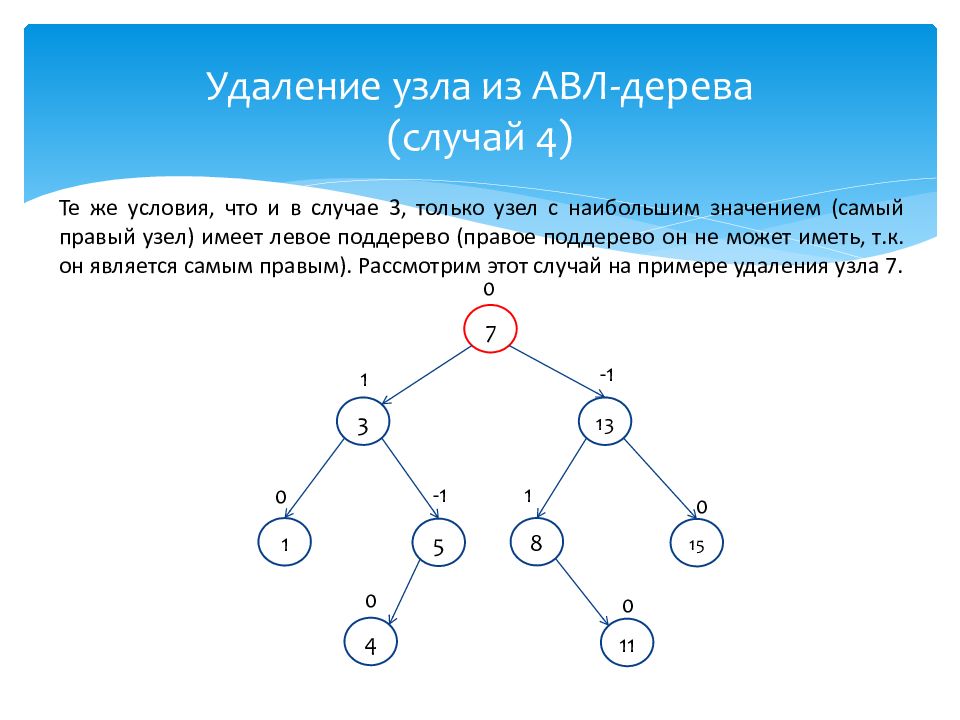
Те же условия, что и в случае 3, только узел с наибольшим значением (самый правый узел ) имеет левое поддерево (правое поддерево он не может иметь, т.к. он является самым правым). Рассмотрим этот случай на примере удаления узла 7. 15 0 7 0 1 0 3 1 4 0 13 -1 5 -1 11 0 8 1
Слайд 75: Удаление узла из АВЛ-дерева (случай 4)
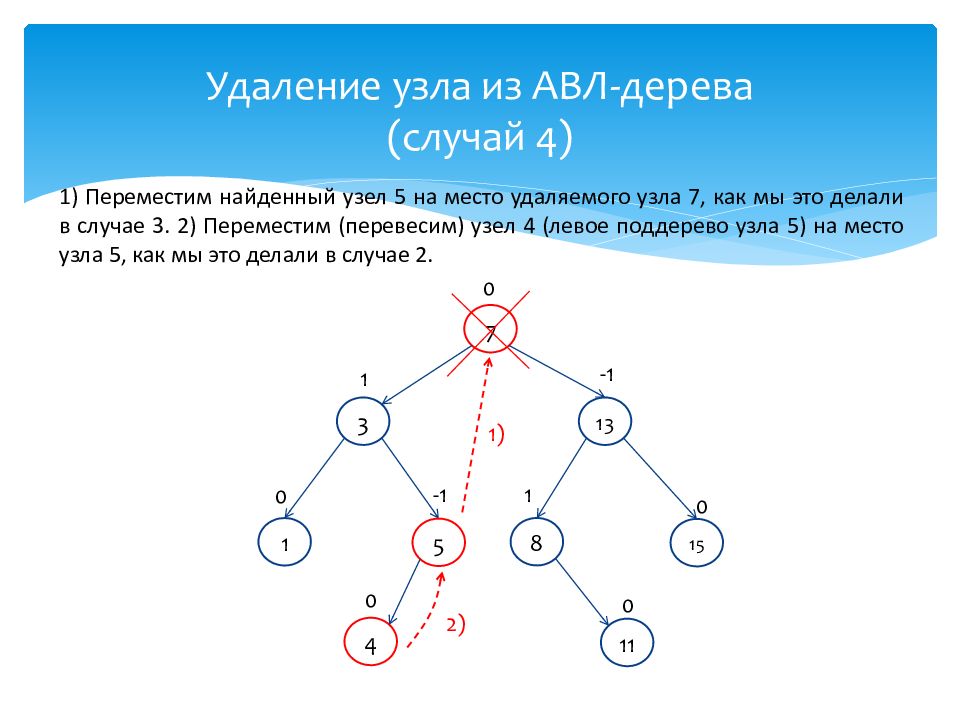
1) Переместим найденный узел 5 на место удаляемого узла 7, как мы это делали в случае 3. 2) Переместим (перевесим) узел 4 (левое поддерево узла 5) на место узла 5, как мы это делали в случае 2. 15 0 7 0 1 0 3 1 4 0 13 -1 5 -1 11 0 8 1 1) 2 )
Слайд 76: Удаление узла из АВЛ-дерева (случай 4)
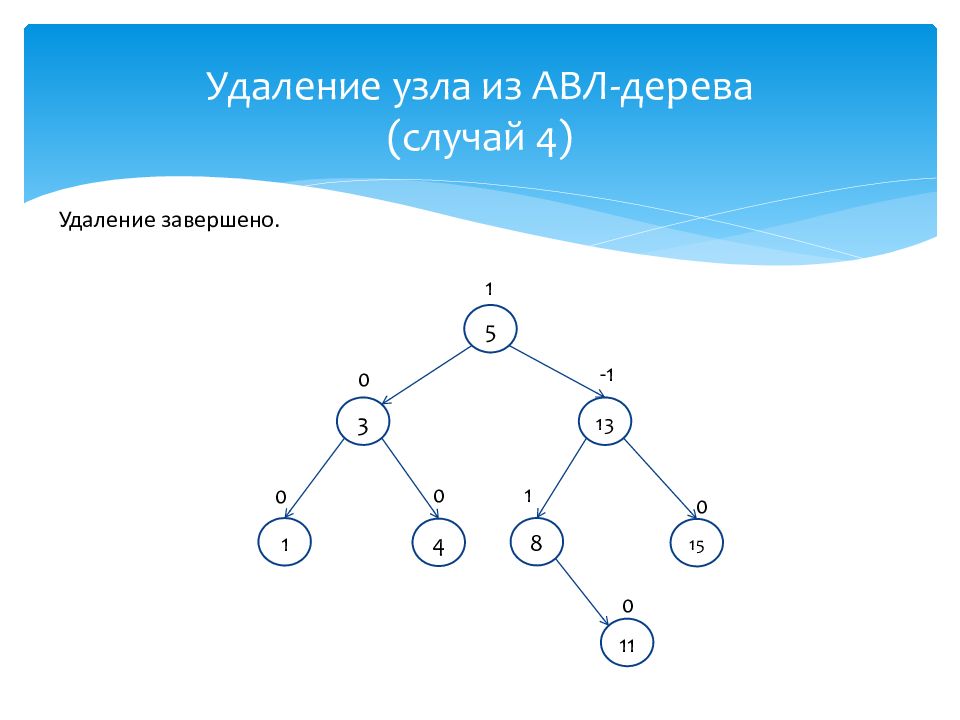
Удаление завершено. 15 0 5 1 1 0 3 0 13 -1 4 0 11 0 8 1
Слайд 77: Выводы
Рассмотрели определение и программную структуру АВЛ-дерева; Научились выполнять построение АВЛ-дерева; Научились осуществлять поиск элемента в АВЛ-дереве на примерах операций добавления, удаления элемента; Научились выполнять операции добавления, удаления узла из АВЛ-дерева. Выводы