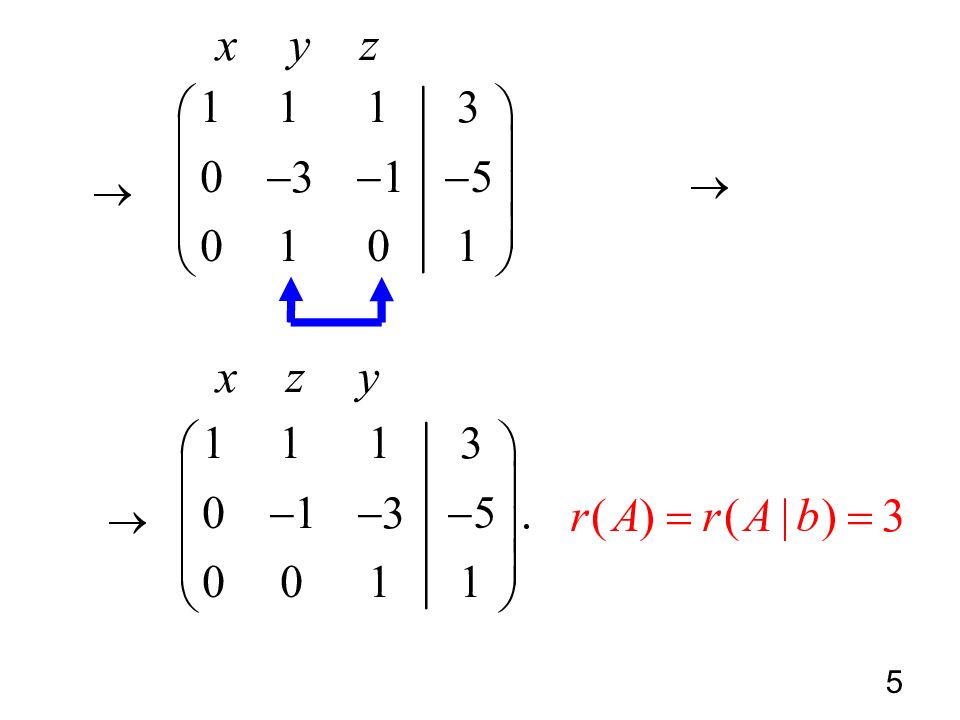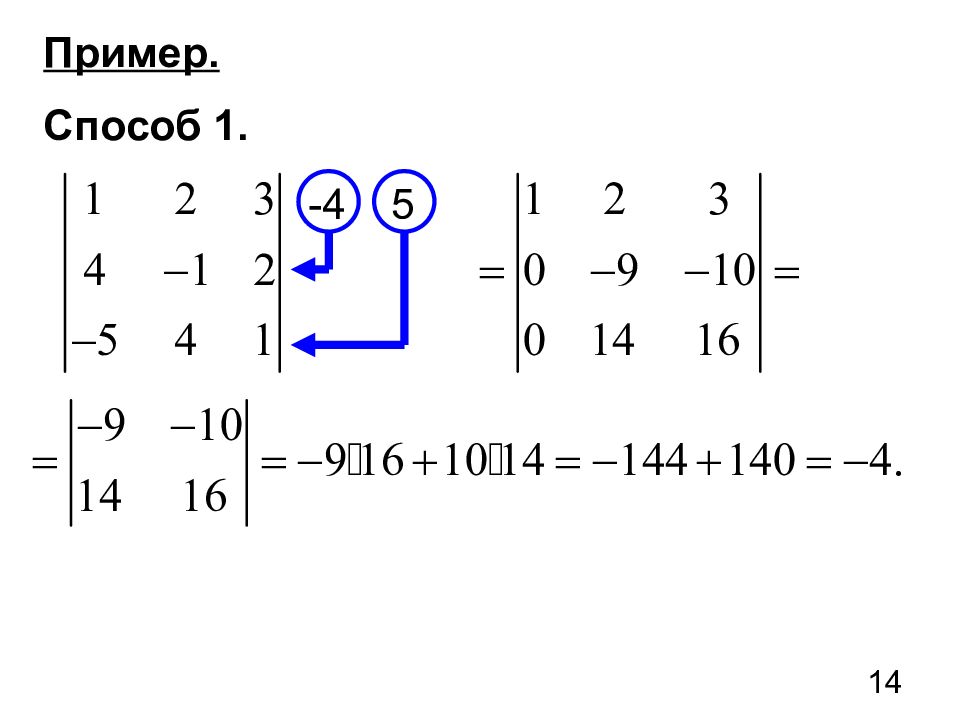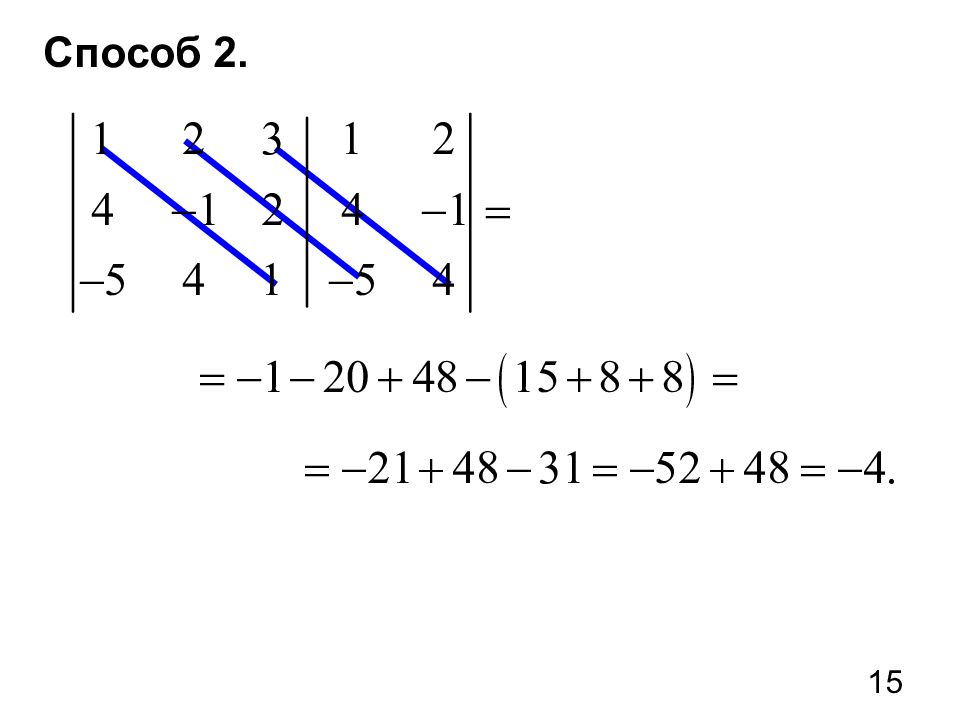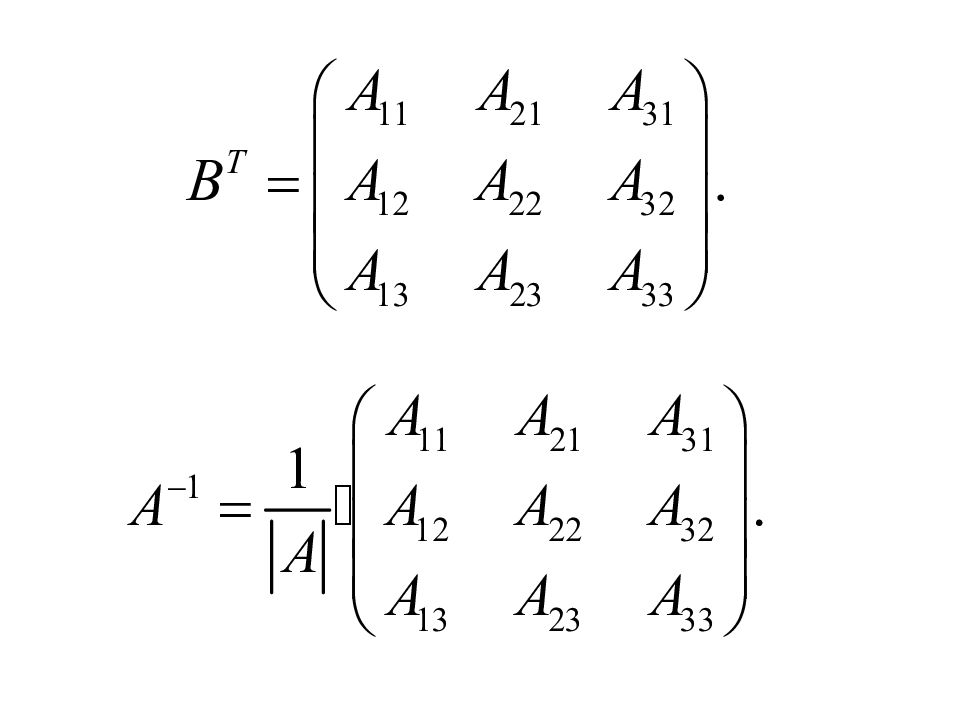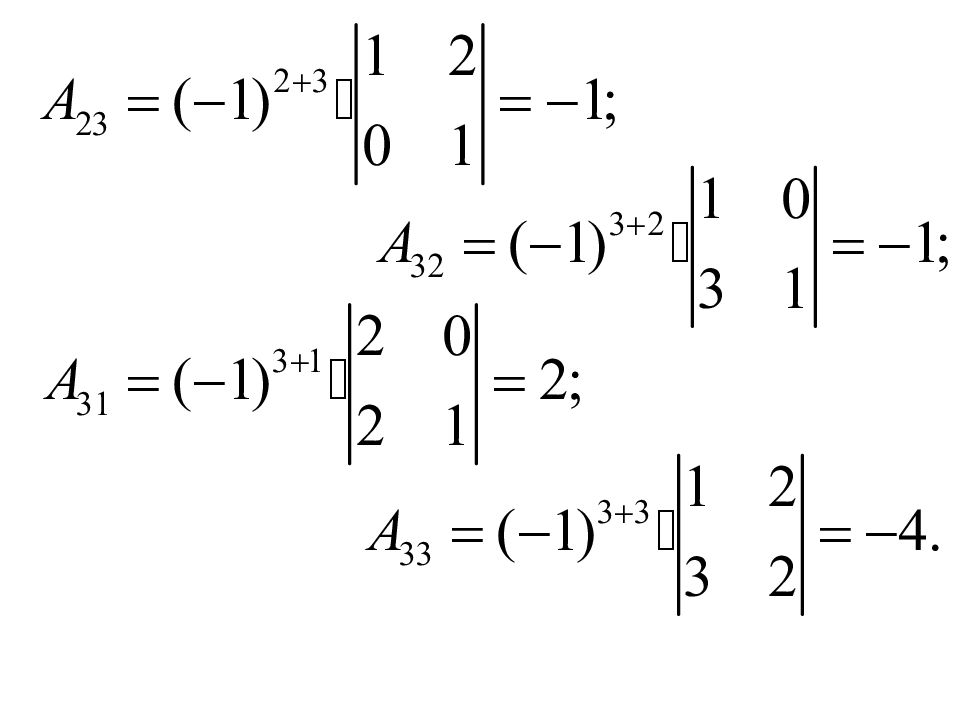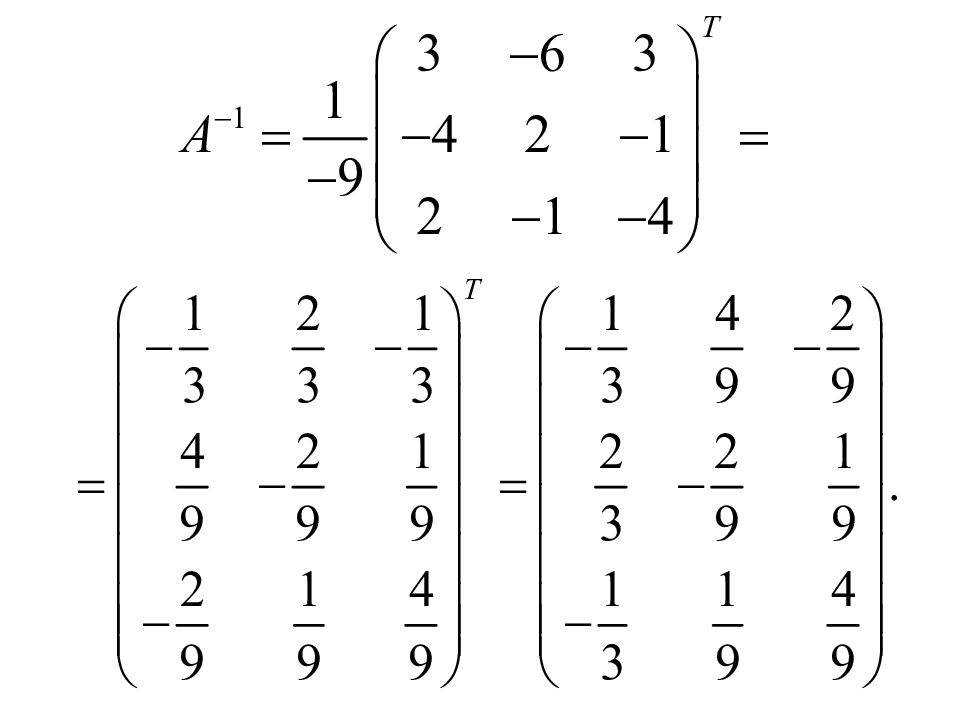1 Лекция N 7 Тема: Метод Гаусса
2 Решение систем линейных уравнений. Метод Гаусса Пример.
3 1) Составим расширенную матрицы системы
4 2) Приведем матрицу к ступенчатому виду -2 +
5
6 3) Составим новую систему Система имеет единственное решение Можно было продолжить преобразования, и привести систему к виду Гаусса.
7 Теорема Кронекера-Капелли. 1) Если, то система не имеет решения 2) Если, где - число неизвестных, то система имеет единственное решение 3) Если, то система имеет бесконечное множество решений.
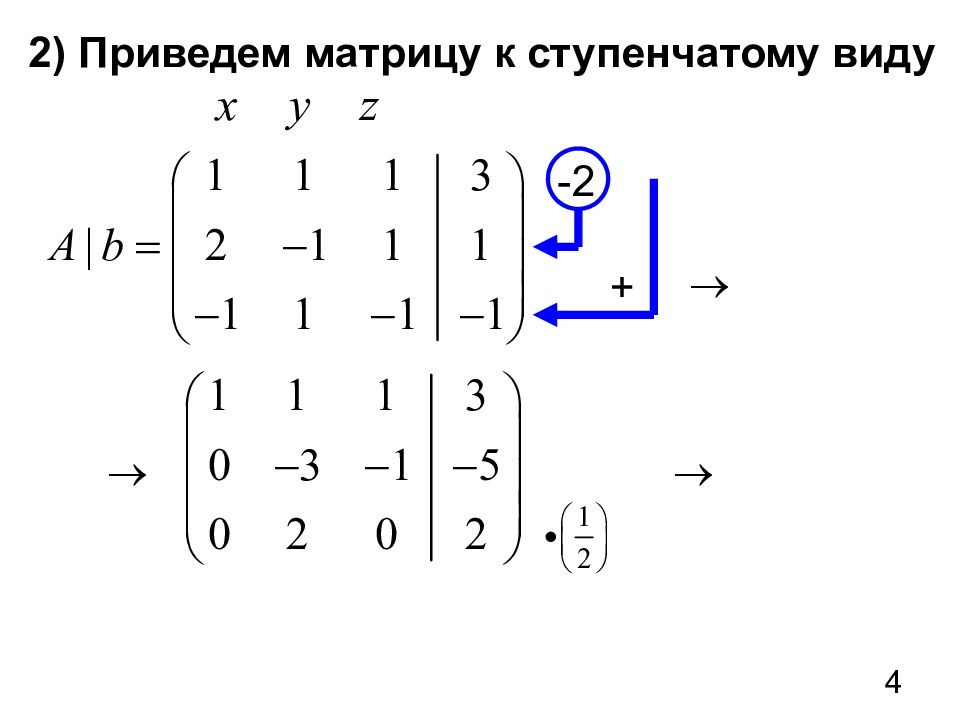
8 Примеры Пример 1. Исследовать на совместность и решить систему методом Гаусса. -5
9 Система имеет бесконечное множество решений. Найдем число свободных неизвестных Базисная неизвестная, свободная. Обозначим свободную неизвестную Получим Ответ:, где
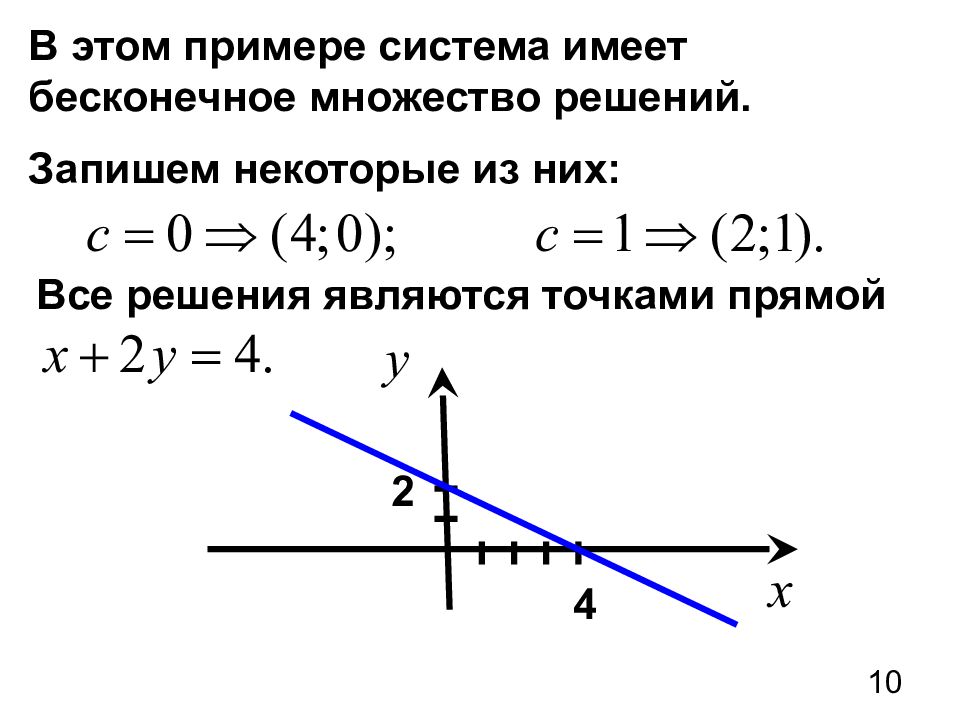
10 В этом примере система имеет бесконечное множество решений. Запишем некоторые из них: Все решения являются точками прямой 4 2
11 Пример 2. Исследовать на совместность и решить систему методом Гаусса. -1 -2
12 Система несовместна (по теореме Кронекера-Капелли) -1
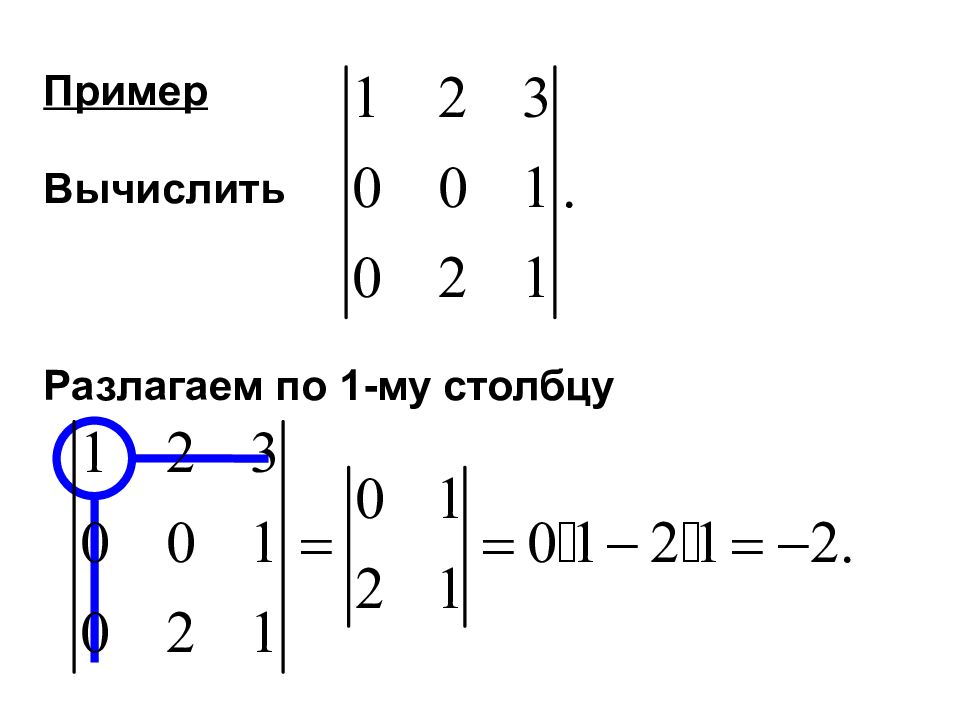
13 Мы рассмотрели два метода решения систем линейных уравнений: 1) Метод Крамера 2) Метод Гаусса Метод Крамера предполагает вычисление определителей. Мы вычисляли определители 3-его порядка разложением по элементам первой строки.
14 Пример. Способ 1. -4 5
15 Способ 2.
16 1) Определитель не изменится, если поменять строки на соответствующие столбцы Свойства определителей 2) Если у определителя 2 одинаковые строки или столбца, то он равен нулю. 3) Если у определителя нулевая строка или столбец, то он равен нулю.
17 4) Если две строки (столбца) поменять местами, то знак определителя изменится на противоположный. Свойства определителей 5) Общий множитель строки (столбца) можно выносить за знак определителя. 6) Определитель не изменится, если к элементам строки (столбца) прибавить элементы другой строки (столбца), умноженные на число.
18 Пример. Вычислить: (т.к. две одинаковые строки)
Пусть дана матрица Определителем второго порядка, соответствующим данной матрице, называется число Определитель обозначают символом
Таким образом, Числа называются элементами определителя Пример
Приведем свойства определителя второго порядка 1. Определитель не изменится, если его строки поменять местами с соответствующими столбцами, т.е.
2. При перестановке двух строк (или столбцов) определитель изменит знак на противоположный, т.е.
3. Определитель с двумя одинаковыми строками (или столбцами) равен нулю. 4. Общий множитель всех элементов строки (или столбца) можно выносить за знак определителя:
5. Если все элементы какой-либо строки (столбца) равны нулю, то определитель равен нулю 6. Если к элементам какой-либо строки (или столбца) определителя прибавить соответствующие элементы другой строки (или столбца), умноженные на одно и то же число, то определитель не изменит своей величины, т.е.
Рассмотрим матрицу Определитель третьего порядка
Определителем третьего порядка называют число
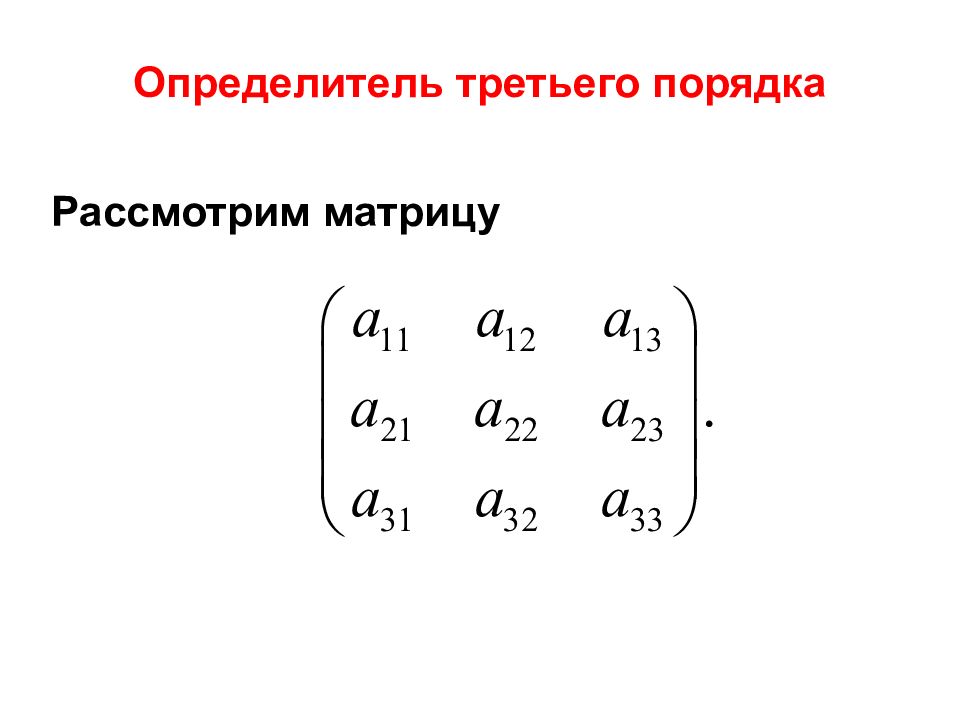
Назовем минором, соответствующим данному элементу определителя третьего порядка, определитель второго порядка, полученный из данного вычеркиванием строки и столбца, на пересечении которых стоит данный элемент. Например, минор соответствующий элементу есть определитель
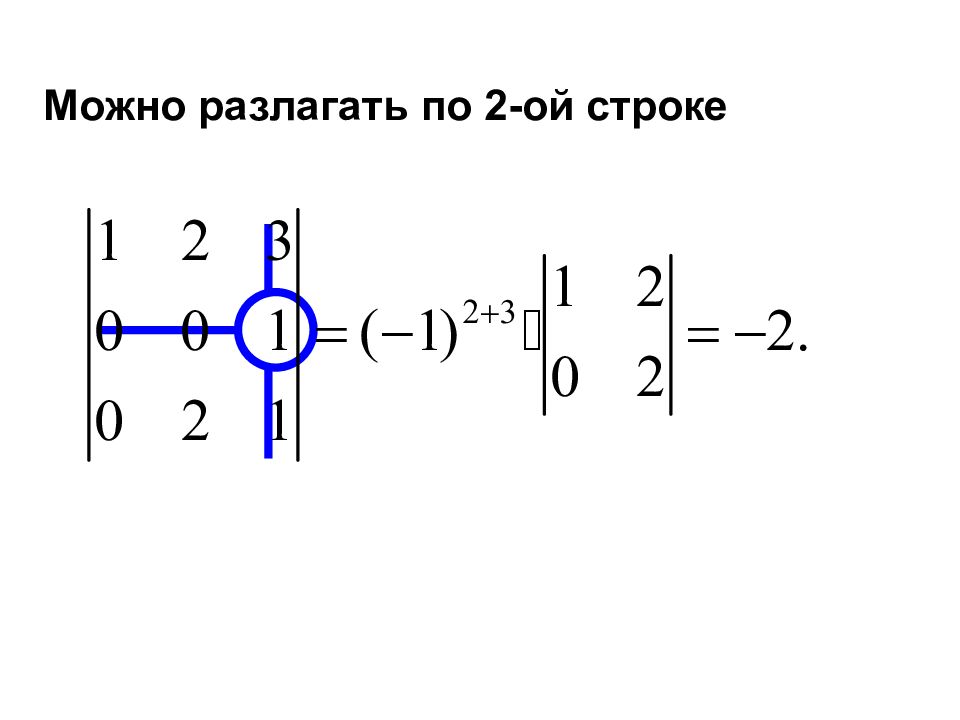
Назовем алгебраическим дополнением Например, Правило. Определитель третьего порядка равен сумме попарных произведений элементов какой-либо его строки (или столбца) на их алгебраические дополнения
Пример Вычислить Разлагаем по 1-му столбцу
Можно разлагать по 2-ой строке
Все свойства определителей 2-ого порядка остаются справедливыми для определителей 3-его порядка. Свойства Пример Вычислить т.к. совпадают первая и вторая строки.
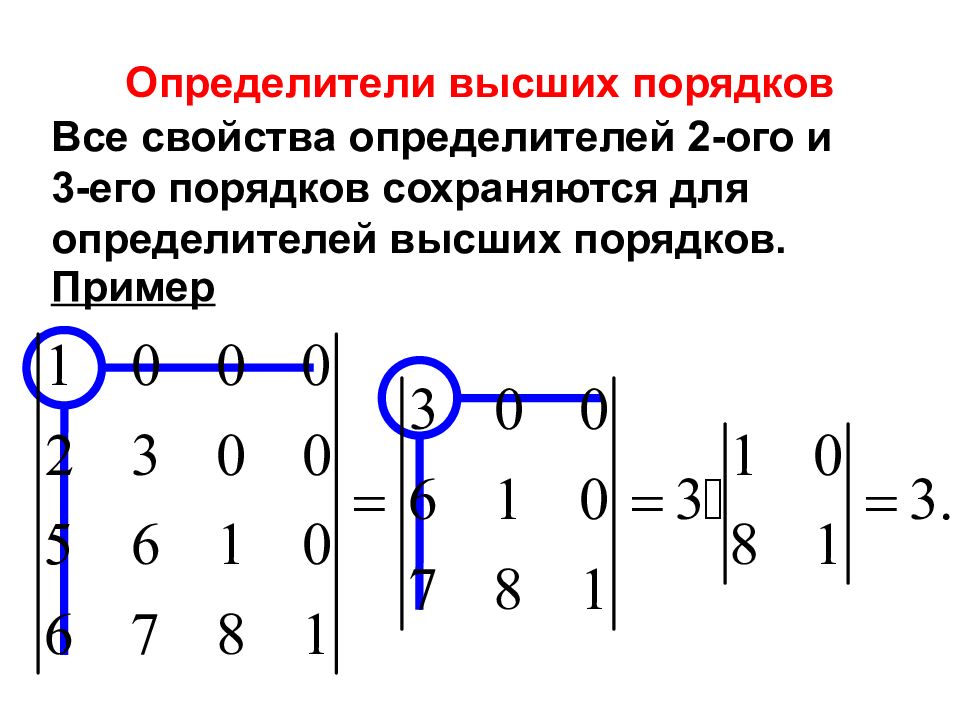
Все свойства определителей 2-ого и 3-его порядков сохраняются для определителей высших порядков. Определители высших порядков Пример
Понятие обратной матрицы вводится только для квадратных матриц. Обратная матрица Опр. Матрица называется обратной к матрице, если - единичная матрица
Теорема. Для того, чтобы квадратная матрица A имела обратную, необходимо и достаточно, чтобы матрица A была невырожденной, т.е. чтобы её определитель был отличен от нуля. Рассмотрим
Составим матрицу из алгебраических дополнений Составим новую матрицу поменяв местами строки и столбцы (матрица называется транспонированной ).
Составим матрицу, обратную матрице второго порядка Здесь Тогда
Пример. то A – невырожденная, и, следовательно, существует обратная матрица
Вычисляем алгебраические дополнения:
Свойства Примеры Вычислить определитель произведения 1. 2.
По свойству 1
Домашнее задание 1. Проверить, что, действительно
Домашнее задание 2. Вычислить
