Слайд 2: Рассматриваемые вопросы
Определение надежности. Количественные показатели надежности. Факторы, определяющие надежность. Классификация моделей надежности. Моделирование и оценка надежности ПС. Статические модели. Динамические модели. Эмпирические модели. МиКПО
Слайд 3: Определение надежности
Надежность – свойство ПС сохранять работоспособность в течение определенного периода времени в определенных условиях эксплуатации с учетом последствий для пользователя каждого отказа. Работоспособное состояние ПС – такое состояние, при котором ПС способно выполнять заданные функции с параметрами, установленными требованиями технического задания. С переходом ПС в неработоспособное состояние связано событие отказа. МиКПО
1. Вероятность безотказной работы – вероятность того, что в пределах заданной наработки отказ системы не наступит. Наработка – продолжительность или объем работы. где – вероятность безотказной работы, – случайное время работы до отказа, – заданная наработка. Внимание: время процессорное! 2. Вероятность отказа – вероятность того, что в пределах заданной наработки отказ системы наступит. МиКПО
Слайд 5: Количественные показатели надежности ( часть 2)
3. Интенсивность отказов – условная плотность вероятности возникновения отказа ПС в определенный момент времени при условии, что до этого времени отказ не возник. – плотность вероятности отказа в момент времени, – число отказов в единицу времени. Если, то. Если, то. МиКПО
Слайд 6: Количественные показатели надежности ( часть 3 )
4. Средняя наработка до отказа – математическое ожидание времени работы ПС до очередного отказа. , где n – количество отказов. 5. Среднее время восстановления – математическое ожидание времени отказа. , где, где – время на локализацию отказа, – время на устранение отказа, – время на проверку работоспособности. 6. Коэффициент готовности – вероятность того, что ПС окажется в работоспособном состоянии в произвольный момент времени его использования по назначению. МиКПО
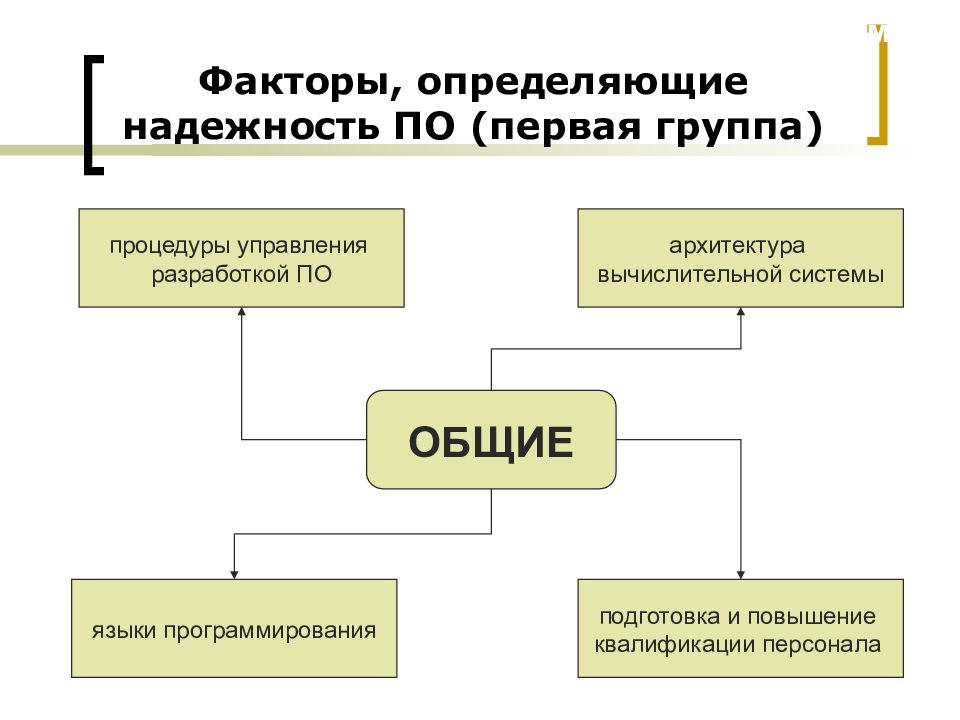
Слайд 7: Факторы, определяющие надежность ПО (первая группа)
ОБЩИЕ процедуры управления разработкой ПО подготовка и повышение квалификации персонала архитектура вычислительной системы языки программирования МиКПО
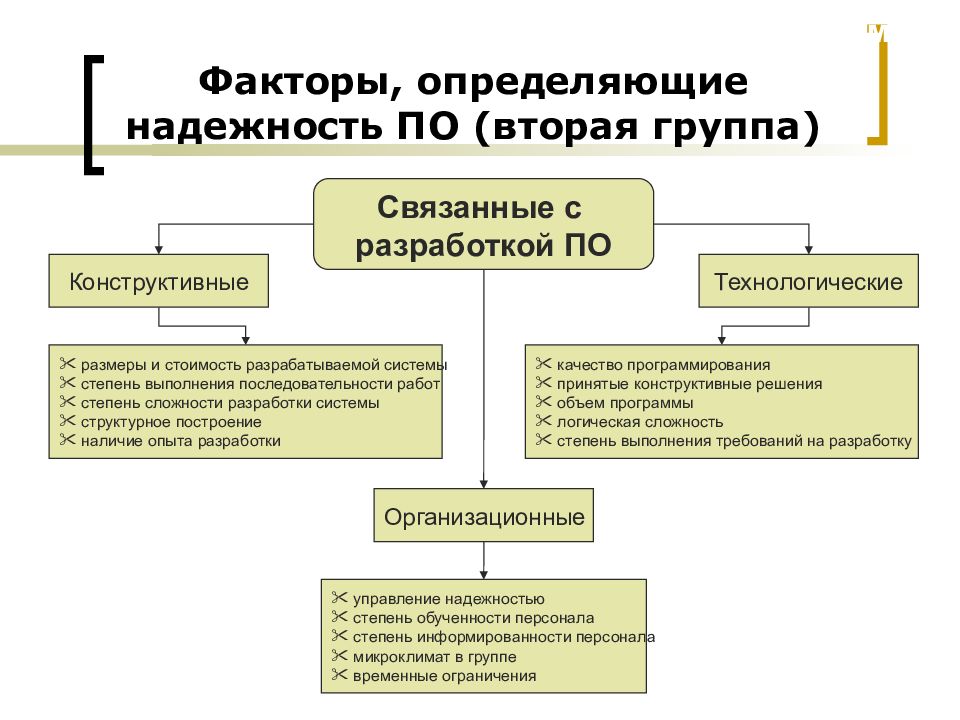
Слайд 8: Факторы, определяющие надежность ПО (вторая группа)
Связанные с разработкой ПО Конструктивные Технологические Организационные Факторы, определяющие надежность ПО (вторая группа) размеры и стоимость разрабатываемой системы степень выполнения последовательности работ степень сложности разработки системы структурное построение наличие опыта разработки качество программирования принятые конструктивные решения объем программы логическая сложность степень выполнения требований на разработку управление надежностью степень обученности персонала степень информированности персонала микроклимат в группе временные ограничения МиКПО
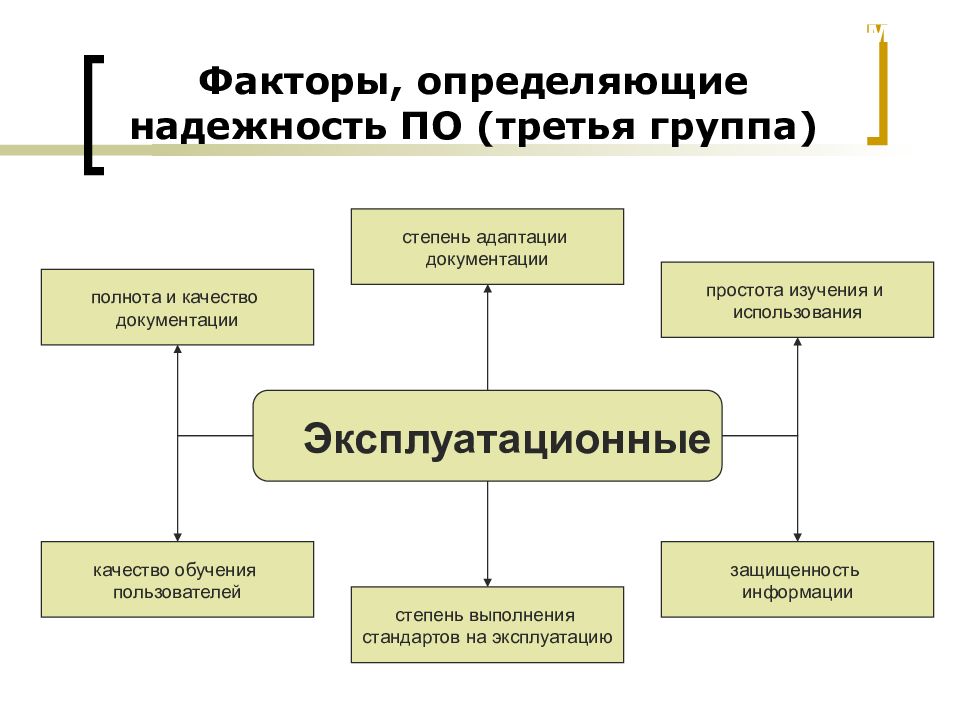
Слайд 9: Факторы, определяющие надежность ПО (третья группа)
Эксплуатационные полнота и качество документации качество обучения пользователей степень адаптации документации простота изучения и использования степень выполнения стандартов на эксплуатацию защищенность информации МиКПО
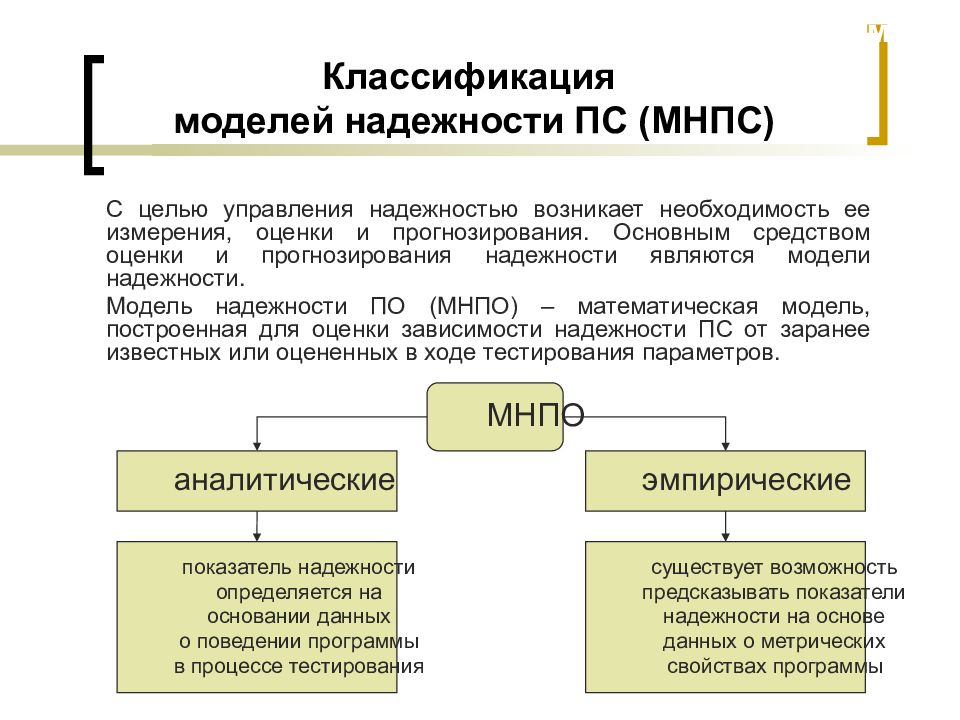
Слайд 10: Классификация моделей надежности ПС (МНПС)
С целью управления надежностью возникает необходимость ее измерения, оценки и прогнозирования. Основным средством оценки и прогнозирования надежности являются модели надежности. Модель надежности ПО (МНПО) – математическая модель, построенная для оценки зависимости надежности ПС от заранее известных или оцененных в ходе тестирования параметров. МНПО аналитические эмпирические показатель надежности определяется на основании данных о поведении программы в процессе тестирования существует возможность предсказывать показатели надежности на основе данных о метрических свойствах программы МиКПО
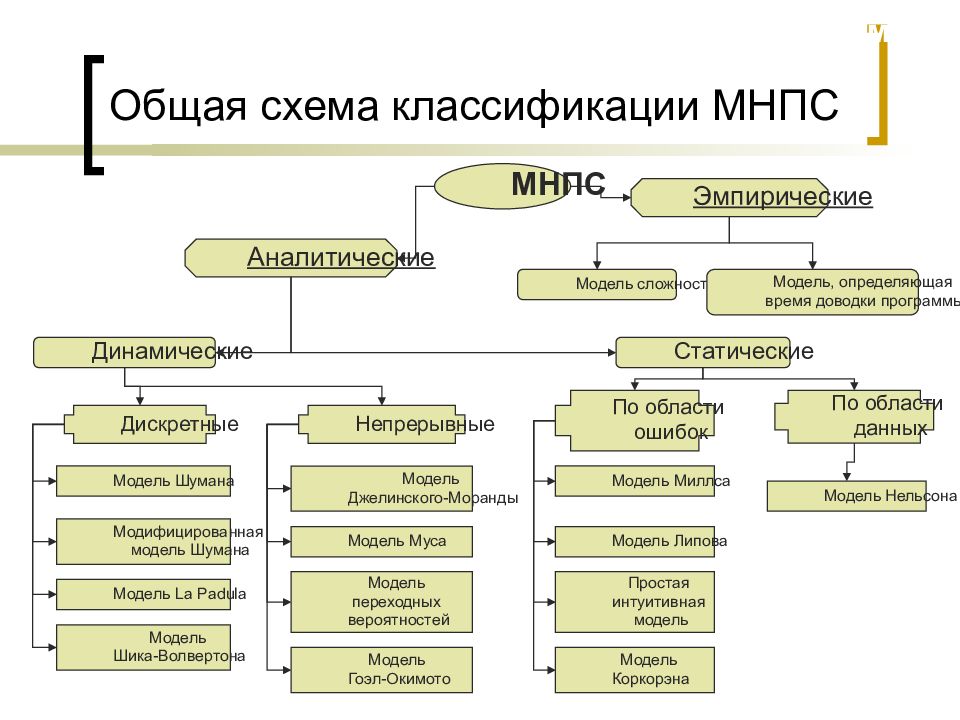
Слайд 11: Общая схема классификации МНПС
МНПС Аналитические Эмпирические Динамические Статические Непрерывные По области ошибок Дискретные По области данных Модель сложности Модель, определяющая время доводки программы Модель Шумана Модифицированная модель Шумана Модель La Padula Модель Шика-Волвертона Модель Джелинского-Моранды Модель Муса Модель переходных вероятностей Модель Гоэл-Окимото Модель Миллса Модель Липова Простая интуитивная модель Модель Коркорэна Модель Нельсона МиКПО
Слайд 12: Аналитические модели надежности ПО
Статические модели (СМ) Появление отказов не связано со временем. СМ по области ошибок – учитывается связь количества ошибок и числа тестовых прогонов. СМ по области данных – учитывается связь количества ошибок с характеристиками входных данных ПС. Динамические модели (ДМ) Поведение отказов зависит от времени. Для использования ДМ необходимо иметь данные о появлении отказов по времени. В ДМ с непрерывным временем (ДНМ) фиксируются интервалы каждого отказа, т.е. получается непрерывная картина появления отказов по времени. В ДМ с дискретным временем (ДДМ) фиксируются число отказов за некоторое время и поведение программы представлено в дискретных точках. МиКПО
Слайд 13: СМ: модель Миллса
Модель Миллса – модель, оценивающая остаточное число ошибок в программе. Состоит из 2 этапов: определение N, т.е. количества оставшихся ошибок проверка гипотезы об N Условно предположим, что в программе имеется не более k собственных ошибок. Искусственно вносим S ошибок. Программа тестируется, пока не будут обнаружены все (или почти все) внесенные ошибки, одновременно фиксируется количество обнаруженных собственных ошибок n. , где V – количество обнаруженных искусственных ошибок , где C – уровень значимости модели, так называемая «мера доверия» По формуле (1) предсказывается возможное число оставшихся в программе ошибок. Формула (2) служит для установления доверительного уровня прогноза. Если не все S найдены, то C рассчитывается по формуле (3): j – число ошибок, найденных при тестировании, принадлежащих подмножеству S МиКПО
Слайд 14: Модель Миллса (задача 1)
Решение. Ответ : с вероятностью 80% можно утверждать, что в программе осталось 2 ошибки. Модель Миллса (задача 1) Дано : k=4; n=2; S=20; V=20; Найти : N - ? C - ? Условие : Предположительно, перед началом тестирования в программе было 4 ошибки, искусственно было внесено ещё 20. В процессе тестирования выявили 20 внесённых и 2 собственные ошибки. Оценить надёжность программы. МиКПО
Слайд 15: Модель Миллса (задача 2)
Решение. Ответ : с вероятностью 33% можно утверждать, что в программе остались от 2 до 3 ошибок. Модель Миллса (задача 2) Дано : k=3; n=2; S= 6 ; V=j=5; Найти : N - ? C - ? Условие : Предположительно, перед началом тестирования в программе было 3 ошибки. Искусственно было внесено ещё 6. В процессе тестирования выявили 5 внесённых и 2 собственные ошибки. Оценить надёжность программы. МиКПО
Слайд 16: Модель Миллса (задача 3 )
Условие : Предположительно, перед началом тестирования в программе было 100 ошибок. Искусственно было внесено ещё 20. В процессе каждого испытания было выявлено определённое количество ошибок (см. табл.) Оценить количество оставшихся ошибок в программе после каждого прогона, а также меру доверия после последнего прогона. Решение. Модель Миллса (задача 3 ) Дано : k= 100 ; S= 20 ; Найти : N - ? C - ? n 25 20 20 15 10 9 1 V 5 4 2 4 2 2 1 МиКПО
Слайд 17: СМ: модель Липова
Модель даёт возможность оценить вероятность присутствия в программе определённого количества ошибок. q – вероятность обнаружения ошибки в каждом тесте при СМ: модель Липова МиКПО где m – количество тестов, проводимых при тестировании q – вероятность обнаружения ошибки в каждом из тестов S – общее количество искусственно внесённых ошибок N – количество собственных ошибок до начала тестирования
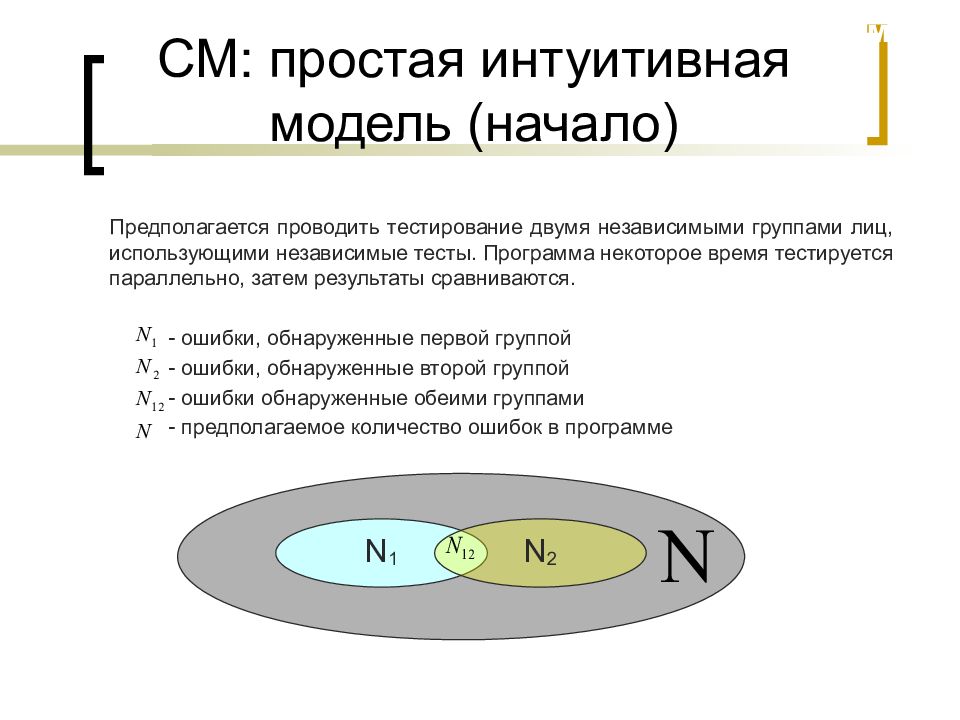
Слайд 18: СМ: простая интуитивная модель (начало)
Предполагается проводить тестирование двумя независимыми группами лиц, использующими независимые тесты. Программа некоторое время тестируется параллельно, затем результаты сравниваются. - ошибки, обнаруженные первой группой - ошибки, обнаруженные второй группой - ошибки обнаруженные обеими группами - предполагаемое количество ошибок в программе МиКПО N 1 N 2
Слайд 19: Простая интуитивная модель (конец)
E 1 и E 2 – эффективности тестирования групп 1 и 2 соответственно N – предположительное число ошибок в программе R – остаточное число ошибок в программе МиКПО
Слайд 20: Простая интуитивная модель (задача)
Условие : При проведении тестирования первой группой было обнаружено 15 ошибок, второй – 25 ошибок. Общих ошибок - 5. Определить надежность по простой интуитивной модели. Решение. Простая интуитивная модель (задача) Дано : N 1 =15; N 2 =25; N 12 =5; Найти : N - ? R - ? МиКПО
Слайд 21: СМ: модель Коркорэна
N 0 – число безотказных испытаний N – число испытаний N i – количество ошибок i- го типа a i – вероятность появления ошибки i- го типа Y i – вероятность появления ошибок Y i =a i, если N i >0 Y i =0, если N i =0 k – известное число типов ошибок R – показатель уровня надёжности Преимущества : легкий расчёт и получение показателя надёжности в виде числа. Недостатки : необходимо знать вероятности появления ошибок в том или ином классе задач. МиКПО
Слайд 22: Модель Коркорэна (задача)
Ответ: с уверенностью в 39% можно утверждать, что программа будет работать без сбоя. Тип ошибки Вероятность появления (a i ) Количество выявленных ошибок 1.Ошибки вычисления ( A ) 0.09 5 2.Логические ошибки ( B ) 0.26 25 3.Ошибки ввода-вывода ( C,E ) 0.16 3 4.Ошибки манипулирования данными ( D ) 0.18 - 5.Ошибки сопряжения ( F ) 0.17 11 6.Ошибки определения данных ( G ) 0.08 3 7.Ошибки в БД ( H ) 0.06 11 Условие : При тестировании программы было проведено 100 испытаний, при которых было выявлено следующее число ошибок по типам (см. табл.). Из 100 испытаний 20 было проведено безуспешно. Необходимо определить надёжность программы. Решение МиКПО
Слайд 23: СМ: Модель Нельсона (начало)
Программа P может быть определена как описание некоторой вычислительной функции F на множестве E всех возможных наборов входных данных таких, что каждый элемент E i представляет собой набор значений данных, необходимых для выполнения прогона программы. Выполнение программы приводит к получению для каждого E i определённого значения функции F(E i ). Множество E определяет все возможные вычисления в программе, т.е. каждому входному тестовому набору соответствует определённый прогон P и наоборот. Наличие ошибок в программе означает, что ей на самом деле соответствует функция F’, отличная от заданной функции F. Для некоторых E i отклонение выхода F’(E i ) от желаемого результата F(E i ) находятся в допустимых пределах. МиКПО
Слайд 24: Модель Нельсона (продолжение)
Для всех оставшихся E i, образующих подмножество E c, выполнение программы не обеспечивает приемлемых результатов (отказ) Если при каждом прогоне на вход программе подаётся один E i тестовый набор данных, то вероятность того, что прогон программы приведёт к отказу равен вероятности того, что набор данных E i, используемый в данном прогоне, принадлежит E c. И эта вероятность равна где Q – вероятность того, что прогон программы на наборе входных данных E i, случайно выбранного из E закончится отказом; n c – число различных значений тестовых данных, принадлежащих E c ( вызывающих отказ); N – общее число входных тестов МиКПО
Слайд 25: Модель Нельсона (продолжение)
Однако, в процессе реального функционирования программы, выбор входных данных диктуется определёнными условиями. Конкретный набор тестовых данных E i может быть выбран с вероятности P i, тогда - прогон заканчивается получением приемлемого результата - прогон заканчивается отказом МиКПО
Слайд 26: Модель Нельсона (конец)
На практике, выбор входных данных для каждого прогона нельзя считать независимым. Поэтому принимают: P ji – вероятность выбора E i набора данных для j- го прогона. Тогда для каждого j- го прогона вероятность того, что он закончится отказом, вычисляется по формуле: Надёжность R(n ) – вероятность того, что в последовательности из n прогонов каждый из прогонов не закончится отказом - формула Нельсона МиКПО
Слайд 27: ДДМ: модель Шумана (начало)
Модель Шумана относится к аналитическим динамическим дискретным моделям. На модель существуют следующие о граничения: Исходное количество ошибок в программе – постоянная величина, которая уменьшается пропорционально тому, как ошибки исправляются. Общее число операторов в программе постоянно. Скорость обнаружения ошибок пропорциональна числу оставшихся ошибок. МиКПО
Слайд 28: Модель Шумана (продолжение)
Предполагается, что до начала тестирования было Е т ошибок. В течение машинного времени отладки устраняется с () ошибок в расчете на один оператор программы. Удельное число ошибок на оператор программы, оставшееся в программе после времени тестирования r () = Е т / I т - с () (1) где I т – известное постоянное, общее число операторов программы. Предполагается, что частота отказов z(t) пропорциональна числу ошибок, оставшихся в программе после отладки: z(t) = C * r () (2) где C – некоторая постоянная, а t – время работы программы без отказов. Функция надежности (вероятность безотказной работы программы на интервале от 0 до t ) рассчитывается по формуле R(t, ) = exp{-C * [E т / I т - с ()] * t} (3) t cp = 1 / (С * [E т / I т - с ()]) (4) где t cp – время безотказной работы программы. МиКПО
Слайд 29: Модель Шумана (продолжение)
В процессе тестирования фиксируются данные об ошибках и времени прогона, которые заносятся в таблицу: № прогона Время прогона Количество ошибок на прогоне … … … n – общее число прогонов, из них: r – безуспешных время прогона: Т 1, Т 2, …, Т r ( n – r ) – успешных время прогона: t 1, t 2, …, t n-r Общее время прогонов H равно: (5) Предполагая, что интенсивность появления ошибок постоянна и равна , получаем: ( 6 ) где A i – количество ошибок на i -ом прогоне. (7) МиКПО
Слайд 30: Модель Шумана (конец)
Имея данные для двух различных моментов тестирования 1 и 2, которые выбираются произвольно с учетом требования с ( 2 ) с ( 1 ), сопоставляют уравнения (4) и (7). Получаем: (8) (9) (10) (11) Получив неизвестные E T и C, можно рассчитать надежность программы по формуле (3). МиКПО
Слайд 31: Модель Шумана (задача)
Условие: в программе имеется 4381 оператор. В процессе последовательных тестовых прогонов были получены следующие данные (см. таблицу). МиКПО № прогона 1 2 A 3 4 5 6 7 8 B 9 10 Количество ошибок 1 2 1 1 1 1 1 2 1 1 Время (м) 5 8 2 1 5 1 1 2 5 5 Найти: вероятность безотказной работы программы в течение времени t = 60 мин при = 35 мин.
Слайд 32: Модель Шумана (решение задачи)
Выберем 2 точки, исходя из требования, чтобы число ошибок, найденных на интервале A–B, было больше, чем на интервале 0 –A. За точку A возьмем 2 прогон, а за точку B – 8 прогон. Тогда ошибки, найденные на этапах тестирования на интервалах 0– A и A–B, будут равны соответственно: ε C ( A ) = 3 / 4381 = 0.0007 ε C ( B ) = 7 / 4381 = 0.0015 Время тестирования на интервалах равно: A = 5 + 8 = 13 B = 2 + 1 + 5 + 1 + 1 + 2 = 12 Рассчитываем интенсивности появления ошибок на двух интервалах: λ A = 3 / 13 = 0.23 λ B = 7 / 1 2 = 0. 58 Это число имеющихся до начала тестирования ошибок. Коэффициент пропорциональности равен: Рассчитаем вероятность безотказной работы в течение времени t при = 35 мин: Возьмем t = 60 мин: МиКПО
Слайд 33: ДДМ: Модифицированная модель Шумана
Не учитывается число операторов в программе. E T и C получают из соотношений: 1) 2) i – время прогона i m – общее число тестовых интервалов m i – число прогонов, завершившихся отказом в i- ом интервале (число ошибок) n i – общее число ошибок, обнаруженных, но не включенных к i -ому интервалу Достоинство модели: можно исправлять ошибки, внося изменения в программу во время тестирования. МиКПО
Слайд 34: ДДМ: модель La Padula
S i – число тестов m i – число отказов во время i- го этапа m – число этапов R – предусмотренная надежность A – параметр роста МиКПО
Слайд 35: ДНМ: модель Муса (начало)
Модель учитывает два вида времени функционирования: суммарное время функционирования, которое отсчитывается в ходе разработки программы, вплоть до того, когда происходит оценка надежности; оперативное время, т.е. время от контрольного момента и далее при условии, что дальнейшего исправления ошибок не будет. Суммарное число обнаруженных и устраненных ошибок: (1) N 0 – первоначальное число ошибок M 0 – общее число отказов, которые могут произойти за все время испытания программы T 0 – средняя наработка на отказ в начале испытания С – коэффициент сжатия тестов (для устранения избыточности при тестировании) – суммарное время функционирования (2) B – коэффициент уменьшения числа ошибок (3) n – число зарегистрированных ошибок m – число зарегистрированных отказов МиКПО
Слайд 36: Модель Муса (конец)
(4) m – число зарегистрированных отказов (5) T – текущее время средней наработки на отказ T 0 – требуемая величина наработки на отказ, задаваемая в договоре заказчиком (6) f – средняя скорость выполнения программы, отнесенная к числу операторов k – коэффициент появления ошибок; характеризует скорость, с которой появились бы ошибки, если бы программа выполнялась линейно; диапазон – от 1.54*10 -7 до 3.99*10 -7 (7) (8) (9) R(t) – надежность для оперативного времени Δ m – число отказов Δ – время тестирования МиКПО
Слайд 37: ДНМ: модель Джелинского-Моранды (начало)
Исходные данные для использования этой модели собираются в процессе тестирования ПС. При этом фиксируется время до очередного отказа. Основное положение, на котором базируется модель, заключается в том, что значение интервалов времени тестирования между обнаружением 2 ошибок имеет экспоненциальное распределение с частотой ошибок (или интенсивностью отказов), пропорциональной числу еще не выявленных ошибок. Каждая обнаруженная ошибка устраняется, число оставшихся ошибок уменьшается на единицу. Функция плотности распределения времени обнаружения i- той ошибки отсчитывается от времени выявления ( i-1 )-ой ошибки : λ i – частота отказов (интенсивность отказов), которая пропорциональна числу еще не выявленных ошибок в программе N – число ошибок, первоначально присутствующих в программе C – коэффициент пропорциональности МиКПО
Слайд 38: Модель Джелинского-Моранды (продолжение)
При заданных значениях λ i рассчитываются P(t i ). Далее экстраполяция кривой функции плотности распределения дает прогнозное значение вероятности появления ошибки на любом временном интервале. N – первоначальное количество ошибок n – общее число удаленных ошибок за все время тестирования Наиболее вероятные значения величин N` и C` (оценки максимального правдоподобия) можно получить на основе данных, полученных при тестировании. Для этого фиксируют время выполнения программы до очередного отказа: t 1, t 2,.. t k. Значения N и C получают решением системы: , где МиКПО
Слайд 39: Модель Джелинского-Моранды (конец)
Поскольку полученные значения N` и C` – вероятностные и точность их зависит от количества интервалов тестирования (или количества ошибок), найденных к моменту оценки надежности, асимптотические оценки дисперсий определяются с помощью следующих формул: где и Чтобы получить числовые значения λ i нужно подставить вместо N и C их возможные значения N` и C`. Рассчитав K значений по формуле (2) и подставив их в формулу (1), можно определить вероятность безотказной работы на различных временных интервалах. На основе полученных расчетных данных строится график зависимости вероятности безотказной работы от времени. МиКПО
Слайд 40: ДДМ: модель Шика-Волвертона (начало)
Модификация модели Джелинского-Моранды для случая возникновения на рассматриваемом интервале более одной ошибки предложена Волвертоном и Шиком. При этом считается, что исправление ошибок производится лишь после истечения интервала времени, на котором они возникли. В основе модели Шика-Волвертона лежит предположение, согласно которому частота ошибок пропорциональна не только количеству ошибок в программах, но и времени тестирования, т.е. вероятность обнаружения ошибок с течением времени возрастает. Частота ошибок (интенсивность обнаружения ошибок) λ i предполагается постоянной в течение интервала времени t i и пропорциональна числу ошибок, оставшихся в программе по истечении (i-1 )-го интервала; но она пропорциональна также и суммарному времени, уже затраченному на тестирование (включая среднее время выполнения программы в текущем интервале. В данной модели наблюдаемым событием является число ошибок, обнаруживаемых в заданном временном интервале, а не время ожидания каждой ошибки, как это было для модели Джелинского-Моранды. МиКПО
Слайд 41: Модель Шика-Волвертона (конец)
Уравнения для определения N` и C` имеют следующий вид: где и t j – продолжительность временного интервала, в котором наблюдается M j ошибок T i-1 – время, накопленное за ( i-1) интервалов N i-1 – суммарное числа ошибок, обнаруженных за период от первого до (i-1)- го интервала времени включительно M – общее число временных интервалов N M – суммарное число обнаруженных ошибок МиКПО
Слайд 42: ДНМ: модель Гоэл-Окимото
Z ( t ) – функция степени риска и она не изменяется по мере возникновения отказов При каждом отказе выявляется и устраняется одна ошибка. a,b – неизвестные константы n – число устраненных ошибок за время тестирования от 0 до Т t i – время i- го отказа E – ожидаемое число ошибок P(t) – функция надежности t – оперативное время МиКПО
Слайд 43: ДНМ: модель переходных вероятностей (начало)
Модель основана на марковском процессе, протекающем в дискретной системе с непрерывным временем. Марковский процесс (процесс без последствий) – процесс в котором для каждого момента времени вероятность любого состояния системы в будущем зависит от состояния во времени t 0 и не зависит от того, каким образом система пришла в это состояние. Последовательность состояний системы ( n, n-1, n-2,..) соответствует периодам времени, когда предыдущая ошибка уже исправлена, а новая – не обнаружена. Последовательность состояний системы ( m, m-1, m-2,..) соответствует периодам времени, когда ошибки исправляются. Ошибки обнаруживаются с интенсивностью λ, а исправляются с интенсивностью μ. p ij – вероятность перехода из одного состояния системы в другое Δ t – бесконечно малое m n n-1 n-2 m-1 1- λ n-1 Δ t 1- λ n Δ t 1- λ n-2 Δ t λ n Δ t 1- μ m Δ t 1- μ m-1 Δ t μ m Δ t λ n-1 Δ t μ m-1 Δ t λ n-2 Δ t m-k+1 n-k+1 n-k n-k-1 m-k 1- λ n-k Δ t 1- λ n-k+1 Δ t 1- λ n-k-1 Δ t λ n-k+1 Δ t 1- μ m-k+1 Δ t 1- μ m-k Δ t μ m-k+1 Δ t λ n-k Δ t μ m-k Δ t λ n-k-1 Δ t μ m-k+2 Δ t МиКПО
Слайд 44: Модель переходных вероятностей (конец)
Вероятности нахождения системы в том или ином состоянии определяются как : Готовность системы определяется как сумма вероятностей нахождения в работоспособном состоянии: Под готовностью системы к моменту времени t понимается вероятность того, что система находится в рабочем состоянии во время t. Надежность системы после времени t отладки, за которое уже выявлено К ошибок, может быть определена из состояния: – интервал времени, когда может появиться (К+1)-я ошибка κ (K) – принятая постоянная интенсивность проявления ошибок МиКПО
Слайд 45: Эмпирические модели
Модель сложности Базируется на свойствах внутренней и внешней связанности модулей. D ij – вероятность того, что модуль i будет изменяться, если модуль j изменяется S i, S j – внутренняя связанность модулей C ij – внешняя связанность модулей Модель, определяющая время доводки программы Позволяет при тестовой сборке системы определить возможное число необходимых исправлений и время, необходимое для доведения ПС до рабочего состояния. p ij – вероятность того, что изменения в i вызовут необходимость изменений в j МиКПО