Слайд 2: 5.1 Трение
Слайд 3: Силы трения
С явлением трения мы знакомы с детства. В разных случаях мы говорим: «В походе не натрите ноги»; в школе — «Сотрите с доски записи». Первые исследования трения были проведе-ны итальянским ученым Леонардо да Винчи более 400 лет тому назад, но результаты его работы не были опубликованы. Законы трения открыли французские ученые Гильом Амонтон (1699 г.) и Шарль Огюстен Кулон (1785 г.).
Слайд 4: Гийом Амонтон
Guillaume Amontons День рождения: 31.08.1663 Место рождения: Париж, Дата смерти: 11.10.1705 Место смерти: Париж, Гражданство: Французский физик и механик, член Французской академии наук (French Academy of Sciences), первооткрыватель концепции абсолютного нуля (-273 °C); один из основателей трибологии, давший свое имя одному из физических явлений в области трения и изобретатель барометра.
Слайд 5: Шарль Огюстен Кулон
(1736-1806) — выдающийся французский инженер и физик, один из основателей электростатики. Исследовал деформацию кручения нитей, установил ее законы. Изобрел (1784) крутильные весы и открыл (1785) закон, названные его именем. Установил законы сухого трения. Экспериментальные исследования Кулона имели основополагающее значение для формирования учения об электричестве и магнетизме. Член Парижской академии наук.
Слайд 6: Трибология - наука о трении
Трибология (от греч. tribo – растираю) - наука, занимающаяся изучением трения и износа узлов машин и механизмов. Результаты научной дея-тельности трибологов касаются явлений, возника-ющих при контакте двух перемещающихся отно-сительно друг друга поверхностей. Как правило, целью трибологических исследований и разрабо-ток является уменьшение износа и предупрежде-ние повреждений трущихся поверхностей путем применения соответствующих смазочных матери-алов и иными способами. Трибология граничит с такими смежными дисциплинами, как теоретичес-кая механика, металловедение, сопротивление материалов, физика, химия и т.п.
Слайд 7: 5.1.1 Трение скольжения
При стремлении сдвинуть одно тело по поверхности другого, в плоскости соприкосновения тел возникает сила сопротивления их относительному движению, называемая силой трения скольжения. В теоретической механике рассматривается только сухое трение, когда между трущимися поверхностями отсутствует смазка. Различают силу трения скольжения при покое и при движении.
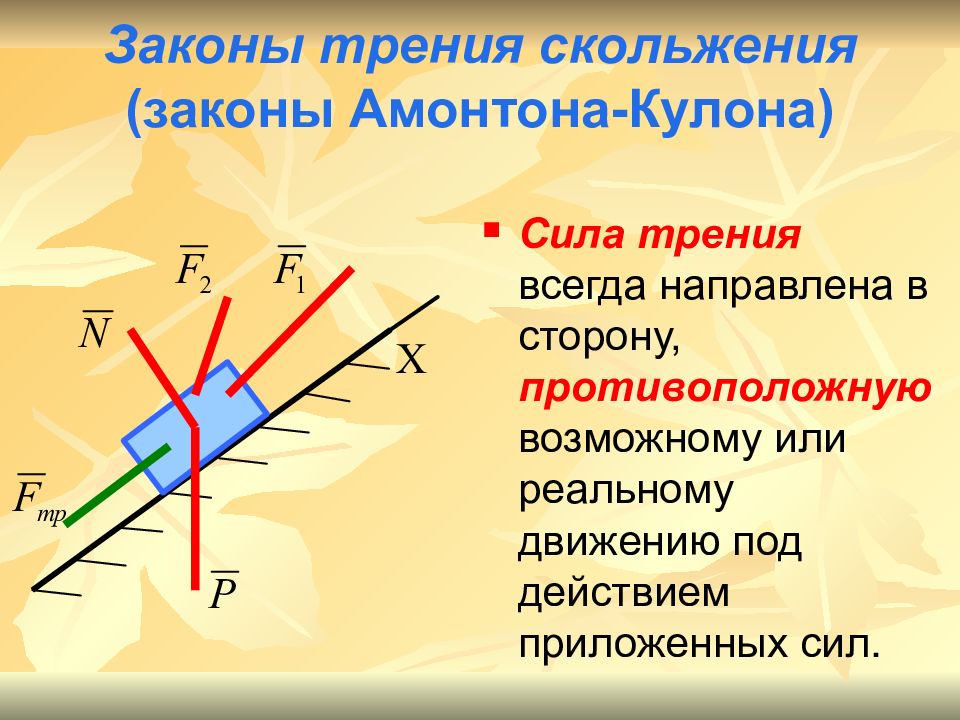
Слайд 8: Законы трения скольжения (законы Амонтона-Кулона)
Сила трения всегда направлена в сторону, противоположную возможному или реальному движению под действием приложенных сил.
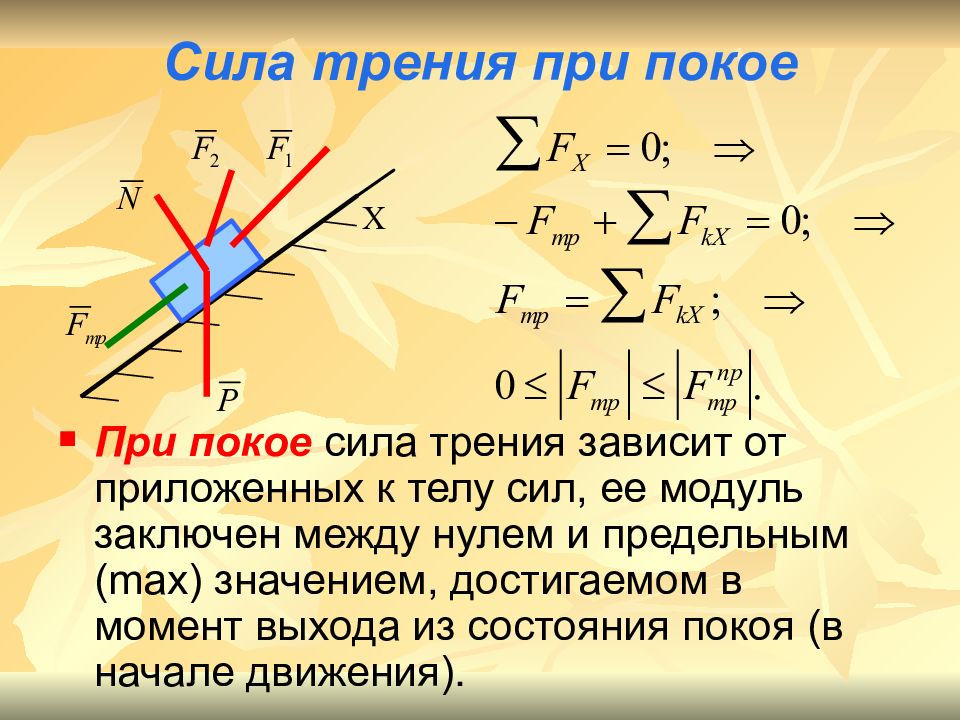
Слайд 9: Сила трения при покое
При покое сила трения зависит от приложенных к телу сил, ее модуль заключен между нулем и предельным ( max ) значением, достигаемом в момент выхода из состояния покоя (в начале движения).
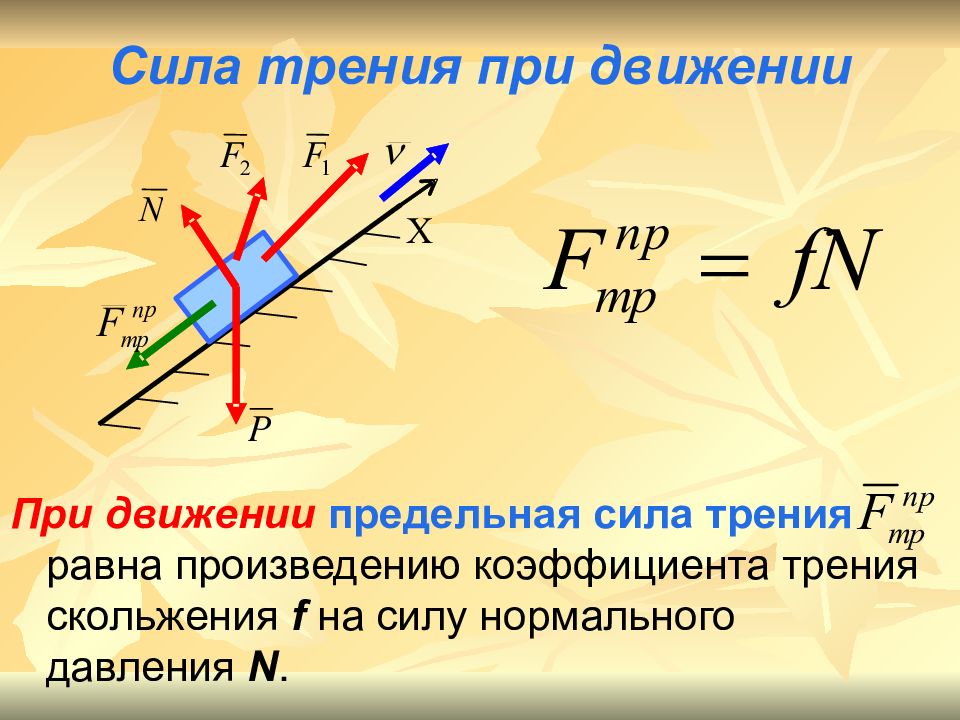
Слайд 10: Сила трения при движении
При движении предельная сила трения равна произведению коэффициента трения скольжения f на силу нормального давления N.
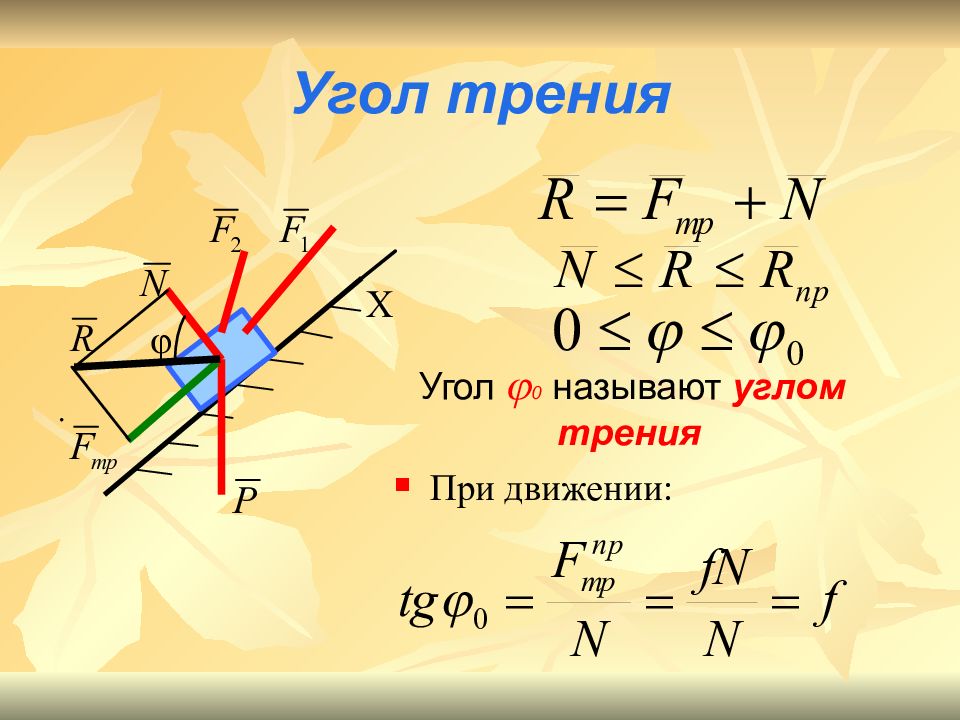
Слайд 11
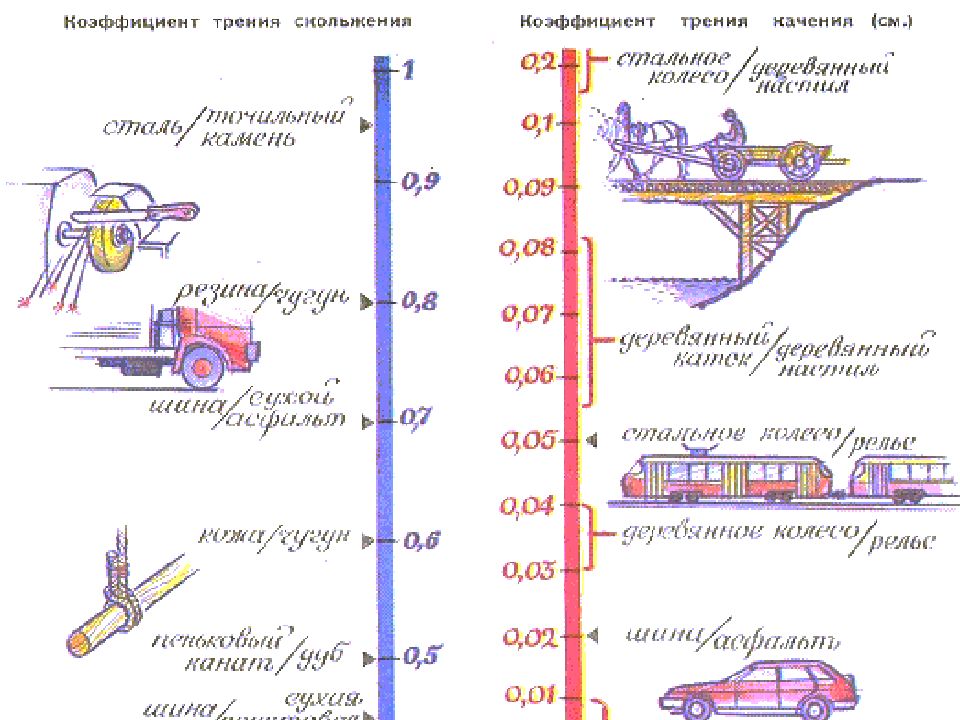
Значение предельной силы трения в довольно широких пределах не зависит от размеров соприкасающихся при трении поверхностей. от скорости зависит незначительно. В приближенных расчетах принимают = const. Коэффициент трения скольжения f определяют экспериментально, так как он зависит от материала и физического состояния трущихся поверхностей.
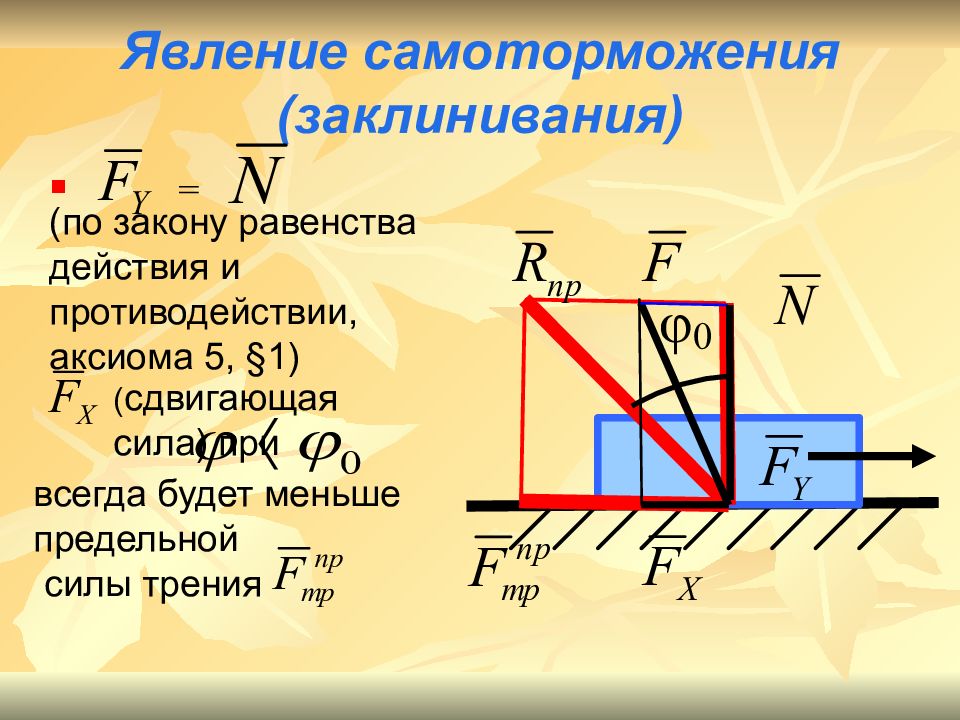
Слайд 13: Явление самоторможения (заклинивания)
= (по закону равенства действия и противодействии, аксиома 5, § 1) ( сдвигающая сила) при всегда будет меньше предельной силы трения
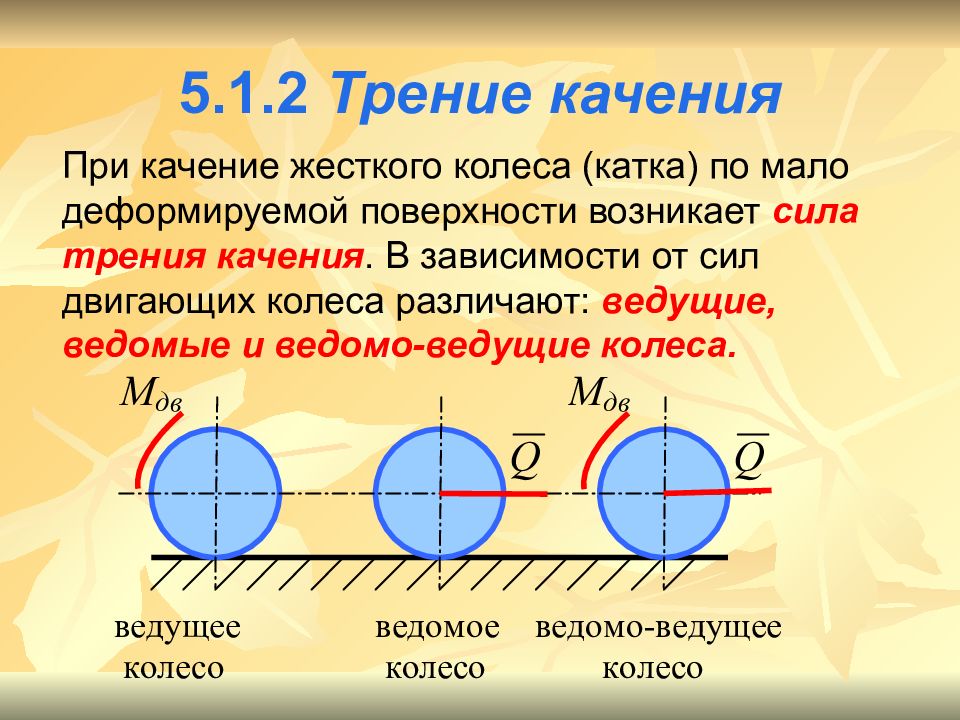
Слайд 14: 5.1.2 Трение качения
При качение жесткого колеса (катка) по мало деформируемой поверхности возникает сила трения качения. В зависимости от сил двигающих колеса различают: ведущие, ведомые и ведомо-ведущие колеса.
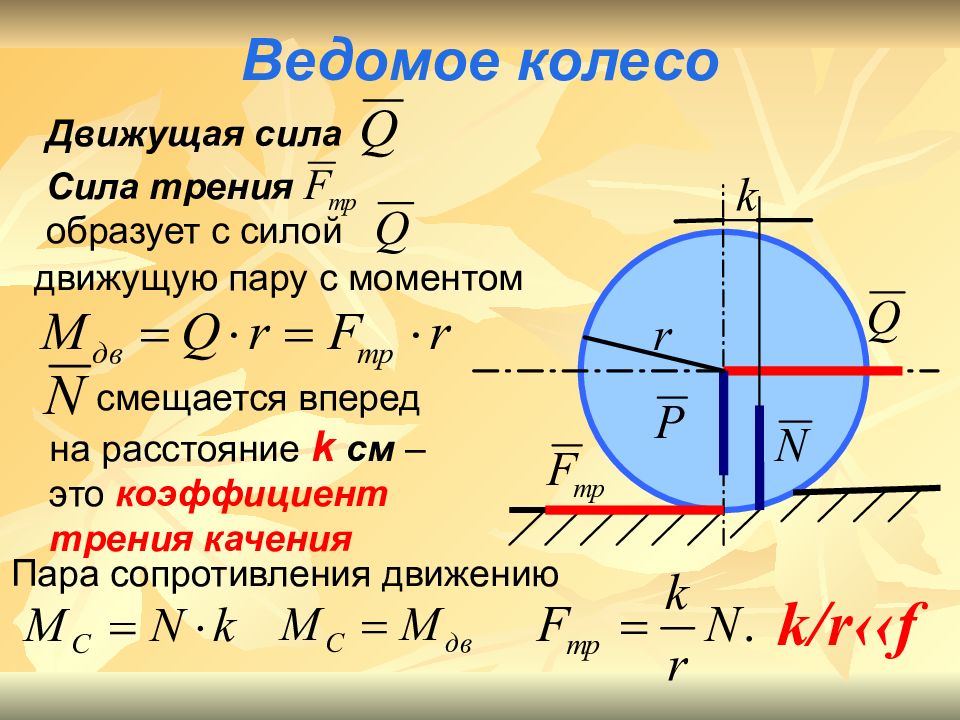
Слайд 15: Ведомое колесо
Движущая сила Сила трения образует с силой движущую пару с моментом смещается вперед на расстояние k см – это коэффициент трения качения Пара сопротивления движению k / r ‹‹ f
Слайд 16: Ведущее колесо
Движущий момент Мдв= F ּ r = F ′ ּ r направлена вперед по движению и образует вместе с силой сопротивления пару Пара сил и с моментом сопротивления
Слайд 17: Качение колеса возможно, если
ведущее колесо не буксует, если так как, то
Слайд 18: Законы трения качения:
Сила трения качения равна Момент сил сопротивления препятствующий качению жесткого колеса в широких пределах не зависит от радиуса колеса. Коэффициент трения качения k зависит от материала катка, плоскости соприкосновения, физического состояния поверхности. В первом приближении считают, что k зависит от угловой скорости колеса (катка) и скорости его скольжения по плоскости. Законы трения качения справедливы для не очень больших нормальных давлений и не слишком легко деформируемых материалов катка и поверхности.
Слайд 19: 5.1.3 Трение верчения
В случае, когда активные силы стремятся вращать тело (шар) вокруг нормали к общей касательной поверхности, возникает трение верчения. Коэффициент трения верчения значительно меньше коэффициента трения качения
Слайд 21: 5.2 Центр тяжести твердого тела
Центр (точка С ) системы параллельных сил тяжести всех точек тела называется центром тяжести твердого тела, а сумма сил тяжести всех его точек называется силой тяжести, действующей на него . Координаты центра тяжести твердого тела:
Слайд 22
Для однородного тела: , где V - объем всего тела; V k - объем k -й частицы. Для однородной тонкой пластины: где S – площадь пластины; S k – площадь k - ой части пластины. Для линии : где L - длина всей линии; L k - длина k -ой части линии.
Слайд 23: Способы определения координат центров тяжести тел:
Теоретические: симметрия; разбиение; дополнение; интегрирование. Экспериментальные: метод подвешивания; метод взвешивания.
Слайд 24
1. Метод разбиения – сложная фигура разбивается на совокупность простых фигур, для которых известны положения центра тяжести или легко определяются :
Слайд 25
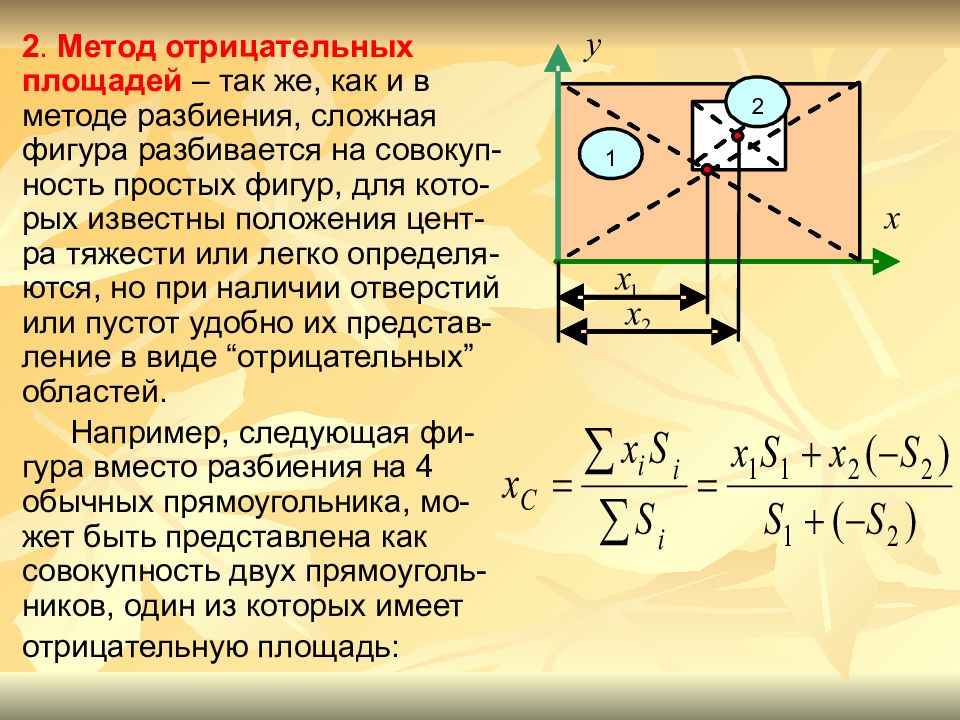
2. Метод отрицательных площадей – так же, как и в методе разбиения, сложная фигура разбивается на совокуп-ность простых фигур, для кото-рых известны положения цент-ра тяжести или легко определя-ются, но при наличии отверстий или пустот удобно их представ-ление в виде “ отрицательных ” областей. Например, следующая фи-гура вместо разбиения на 4 обычных прямоугольника, мо-жет быть представлена как совокупность двух прямоуголь-ников, один из которых имеет отрицательную площадь :
Слайд 26
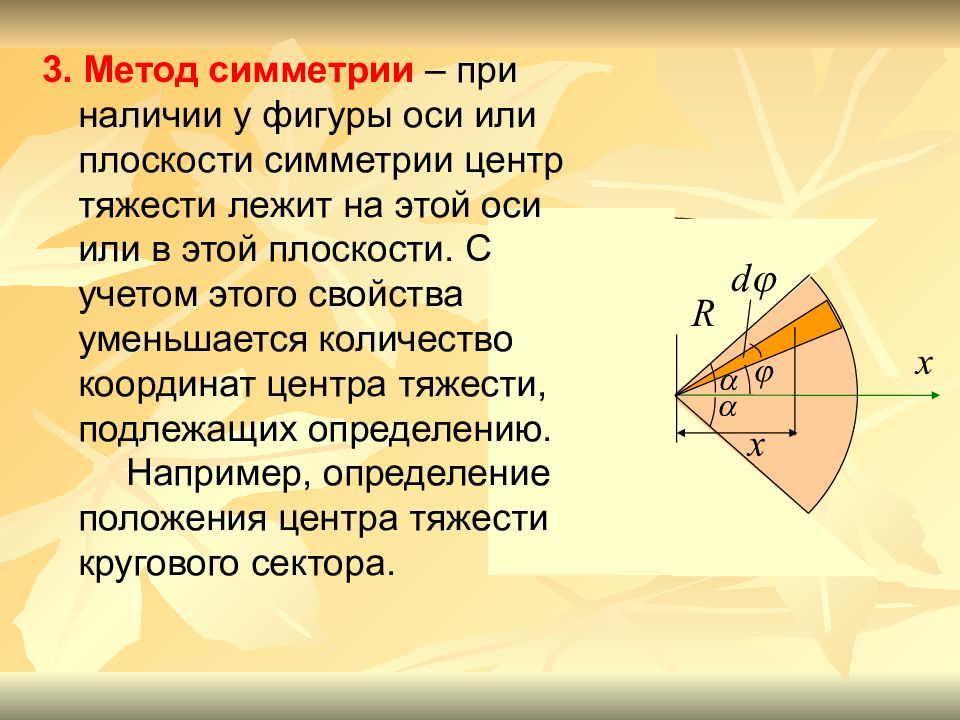
3. Метод симметрии – при наличии у фигуры оси или плоскости симметрии центр тяжести лежит на этой оси или в этой плоскости. С учетом этого свойства уменьшается количество координат центра тяжести, подлежащих определению. Например, определение положения центра тяжести кругового сектора.
Слайд 27
4. Метод интегрирования – при наличии у фигуры достаточно простого контура, описываемым известным уравнением (окружность, парабола и т.п.), выбирается элементарная площадка или полоска и выполняется аналитическое интегрирование. См. например, определение положения центра тяжести треугольника или кругового сектора. При более сложном контуре, который может быть разбит на более простые граничные отрезки используется предварительно метод разбиения. При сложностях с аналитическим интегрированием используются численные методы интегрирования.
Слайд 28
5. Метод подвешивания – экспериментальный метод, основанный на том, что при подвешивании тела или фигуры за какую-либо произвольную точку центр тяжести находится на одной вертикали с точкой подвеса. Для определения положения центра тяжести плоской фигуры достаточно ее подвесить поочередно за две любые точки и прочертить соответствующие вертикали, например, с помощью отвеса, и точка пересечений этих прямых соответствует положению центра тяжести фигуры.
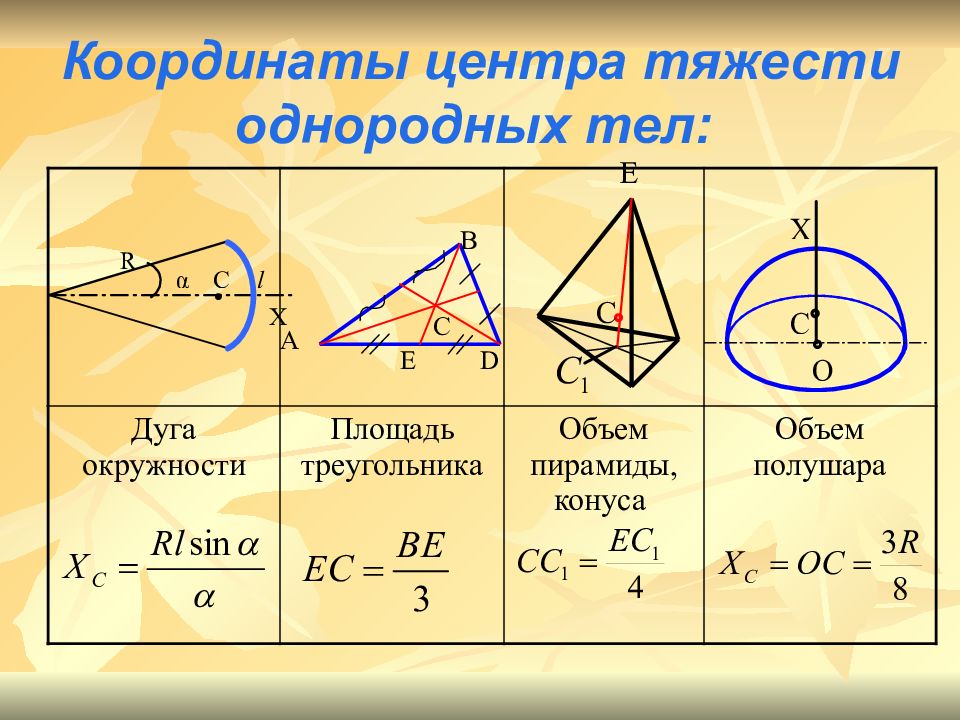
Слайд 29: Координаты центра тяжести однородных тел:
Дуга окружности Площадь треугольника Объем пирамиды, конуса Объем полушара
Слайд 30: 5.3 Статическая устойчивость 5.3.1 Устойчивость при опрокидывании
При равновесии ; - удерживающий момент; - опрокидывающий момент. При устойчивом состоянии На границе устойчивости - коэффициент устойчивости