Слайд 2: Содержание
1.Ответь на вопросы 2.Вспомни признаки равенства треугольников 3.Проверим определения 4.Реши задачи 5.Подумай и ответь Источники
накрест лежащие углы равны соответственные углы равны смежные углы равны вертикальные углы равны односторонние углы равны
Слайд 5: 2)Если две параллельные прямые пересечены секущей, то
сумма накрест лежащих углов равна 180* сумма односторонних углов равна 180* сумма соответственных углов равна 180* сумма смежных углов равна 180* сумма вертикальных углов равна 180*
Слайд 6: 3)Если при пересечении двух прямых секущей соответственные углы равны, то
прямые перпендикулярны прямые параллельны являются продолжением друг друга накладываются одна на другую прямые не пересекаются
Слайд 7: 4)Сумма смежных углов треугольника
равна 360* равна180* равна 90* равна 70* равна 140*
Слайд 8: 5)Сумма углов треугольника
равна 360* равна180* равна 90* равна 120* равна 140*
Слайд 10: 6)Вспомни признак равенства треугольника
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны
Слайд 11: 7)Вспомни признак равенства треугольника
Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого треугольника, то такие треугольники равны.
Слайд 12: 8)Вспомни признак равенства треугольника
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
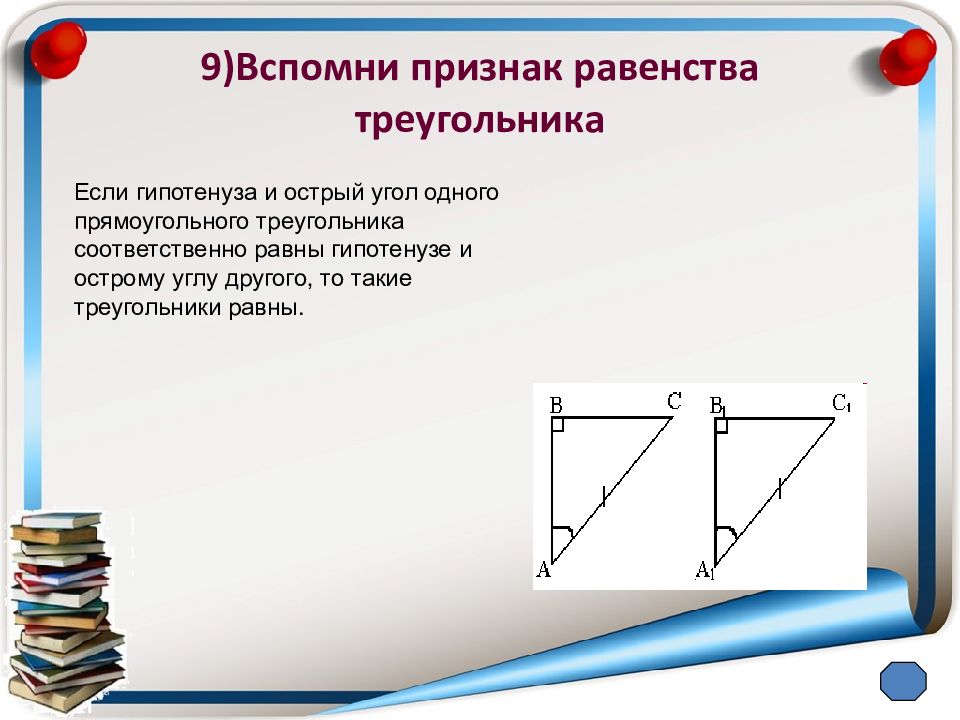
Слайд 13: 9)Вспомни признак равенства треугольника
Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны.
Слайд 14: 10)Вспомни признак равенства треугольника
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
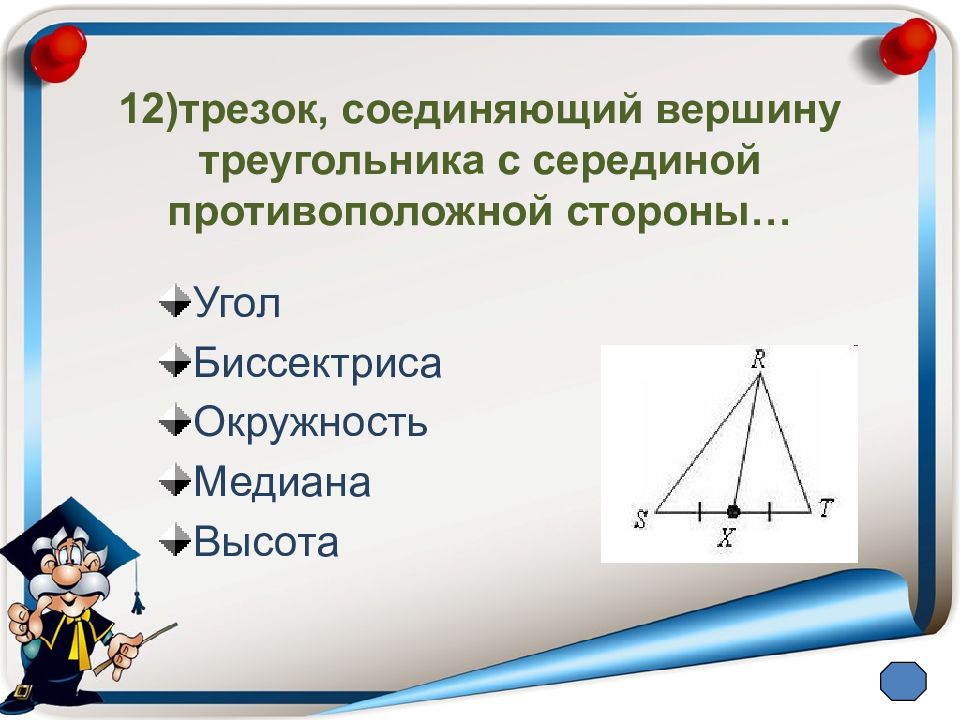
Угол Биссектриса Окружность Медиана Высота
Слайд 16: 12) трезок, соединяющий вершину треугольника с серединой противоположной стороны…
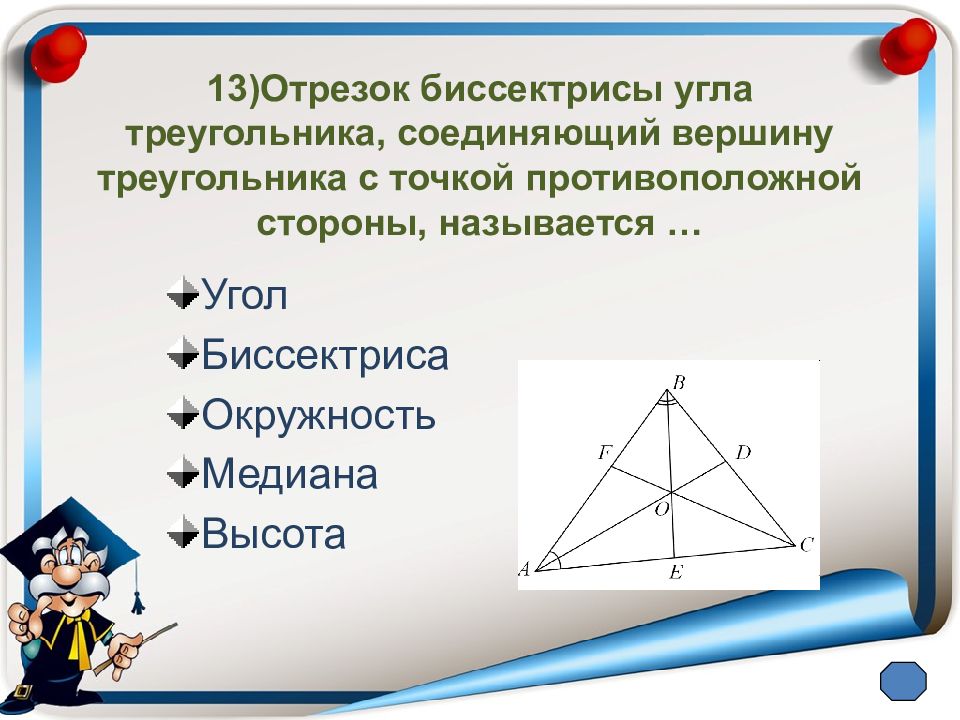
Угол Биссектриса Окружность Медиана Высота
Слайд 17: 13)Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется …
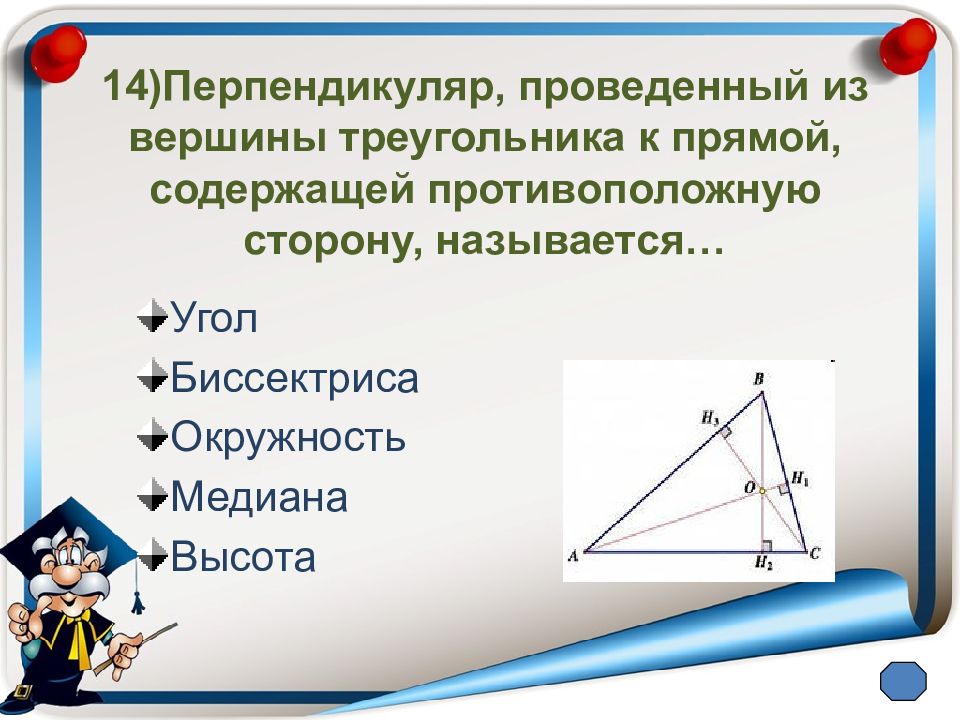
Угол Биссектриса Окружность Медиана Высота
Слайд 18: 14)Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется…
Угол Биссектриса Окружность Медиана Высота
Угол Биссектриса Окружность Медиана Высота
Слайд 20: Реши задачи и проверь свои ответы
1. Сумма вертикальных углов MOE и D ОС, образованных при пересечении прямых MC и DE, равна 204*. Найдите угол MOD. 2. Отрезок DM – биссектриса треугольника CDE. Через точку М проведена прямая, параллельная стороне CD и пересекающая сторону DE в точке N. Найдите углы треугольника DMN, если угол CDE равен 68*. 3.В треугольнике CDE с углом E, равным 32* проведена биссектриса CF, угол CFD равен 72*. Найдите угол D. 4.Периметр равнобедренного тупоугольного треугольника равен 45см, а одна из его сторон больше другой на 9см. Найдите стороны треугольника. 5.В остроугольном треугольнике MNP биссектриса угла M пересекает высоту NK в точке О, причем ОК равно 9см. Найдите расстояние от точки О до прямой MN. 12см, 12см 31см 34*,34*, 112* 78* 9 см 68*