Методическая разработка Савченко Е.М. МОУ гимназия №1, г. Полярные Зори, Мурманской обл. Л.С. Атанасян Геометрия 7 класс. Второй признак равенства треугольников
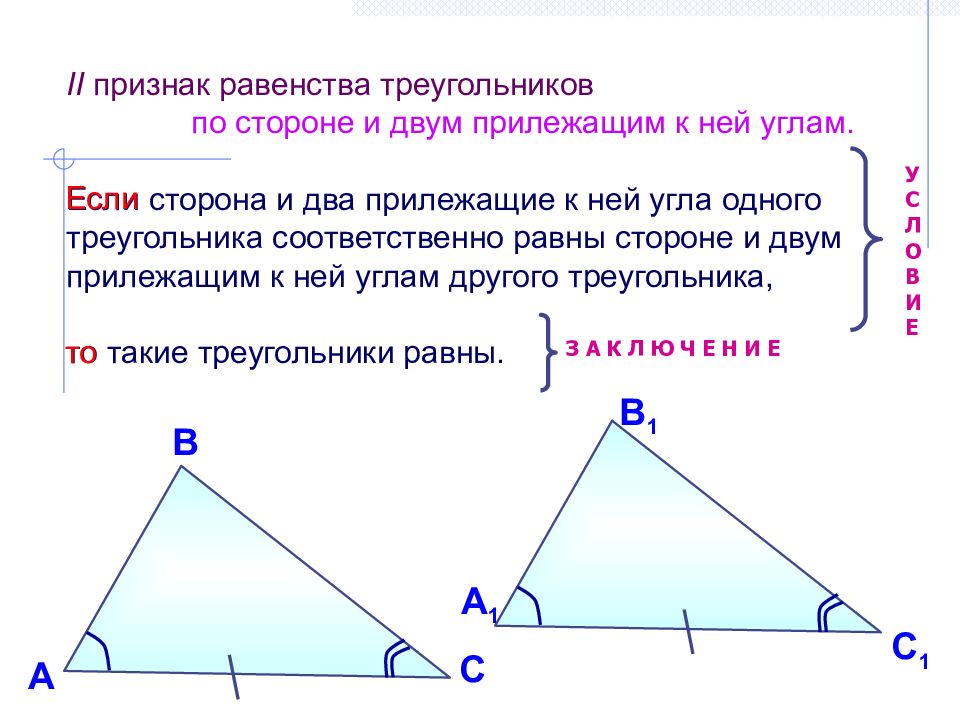
II признак равенства треугольников по стороне и двум прилежащим к ней углам. Если сторона и два прилежащие к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны. У С Л О В И Е З А К Л Ю Ч Е Н И Е С 1 А В С А 1 В 1 Если то
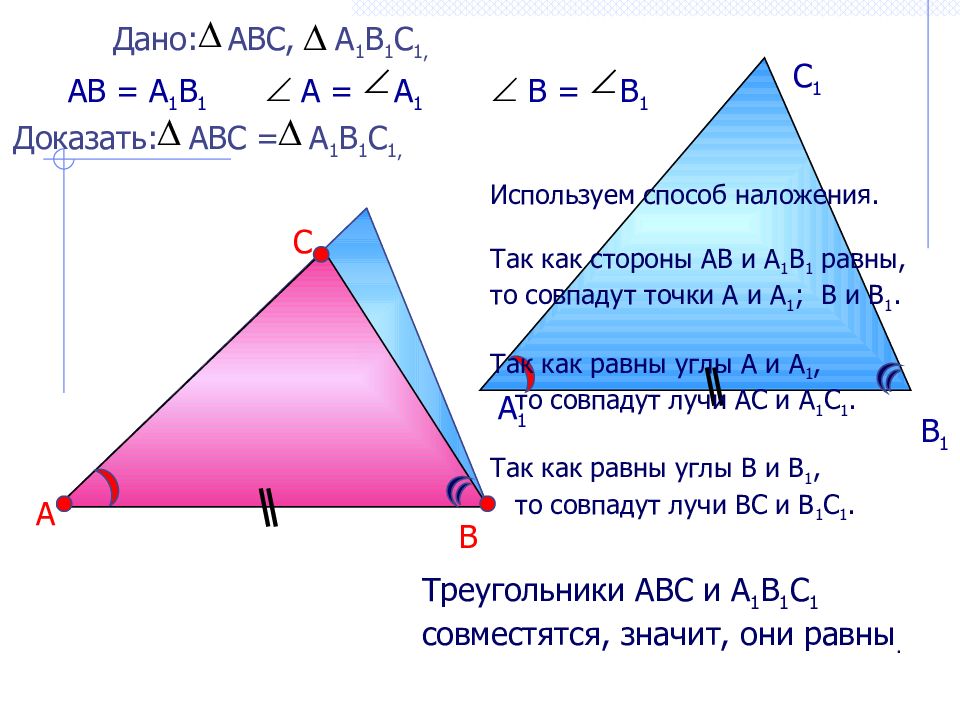
Дано: АВС, А 1 В 1 С 1, А В С А 1 В 1 С 1 АВ = А 1 В 1 А = А 1 Доказать: АВС = А 1 В 1 С 1, Треугольники АВС и А 1 В 1 С 1 совместятся, значит, они равны. В = В 1 Используем способ наложения. Так как стороны АВ и А 1 В 1 равны, то совпадут точки А и А 1 ; В и В 1. Так как равны углы А и А 1, то совпадут лучи АС и А 1 С 1. Так как равны углы В и В 1, то совпадут лучи ВС и В 1 С 1.
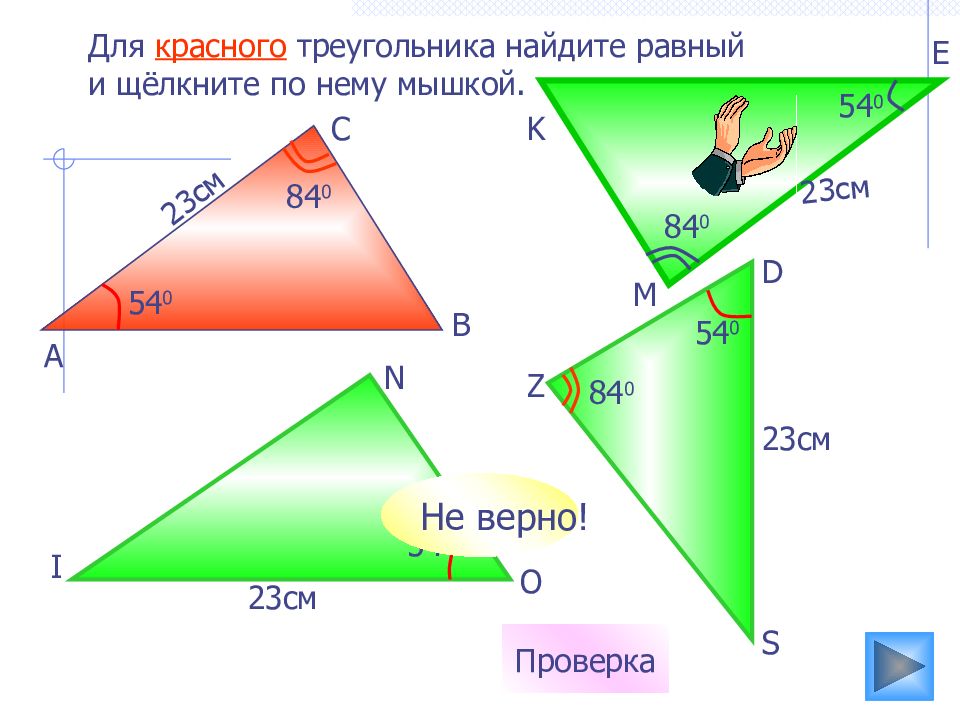
23см 54 0 Для красного треугольника найдите равный и щёлкните по нему мышкой. 23см 23см 54 0 23см 54 0 84 0 84 0 84 0 Проверка 54 0 Не верно! S K D А N I O C B M E Z
А В С D Доказать: АВС = С DO
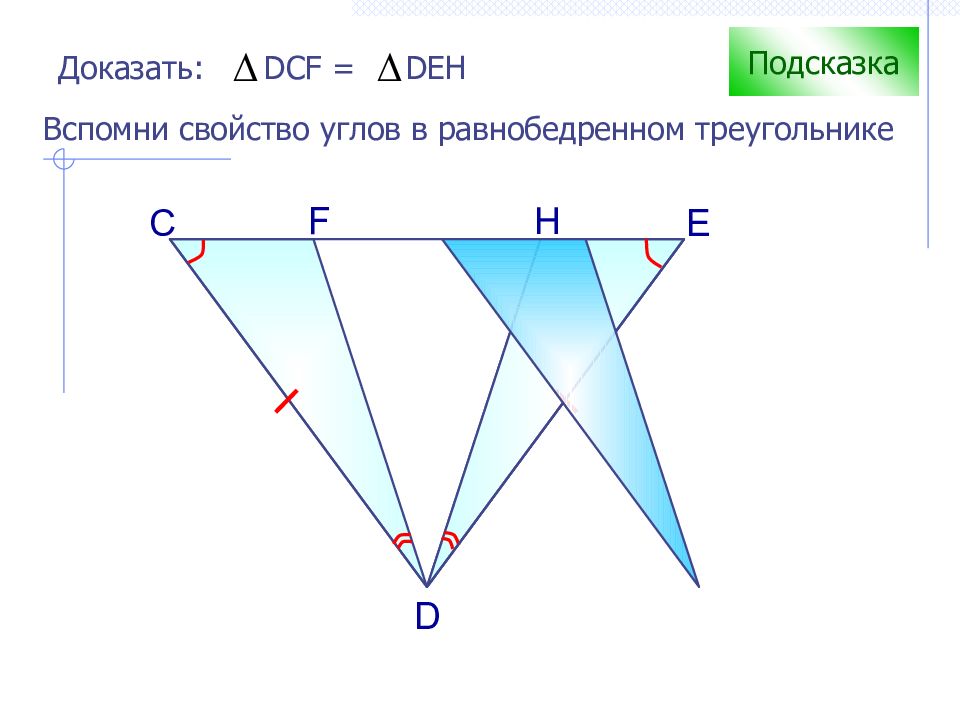
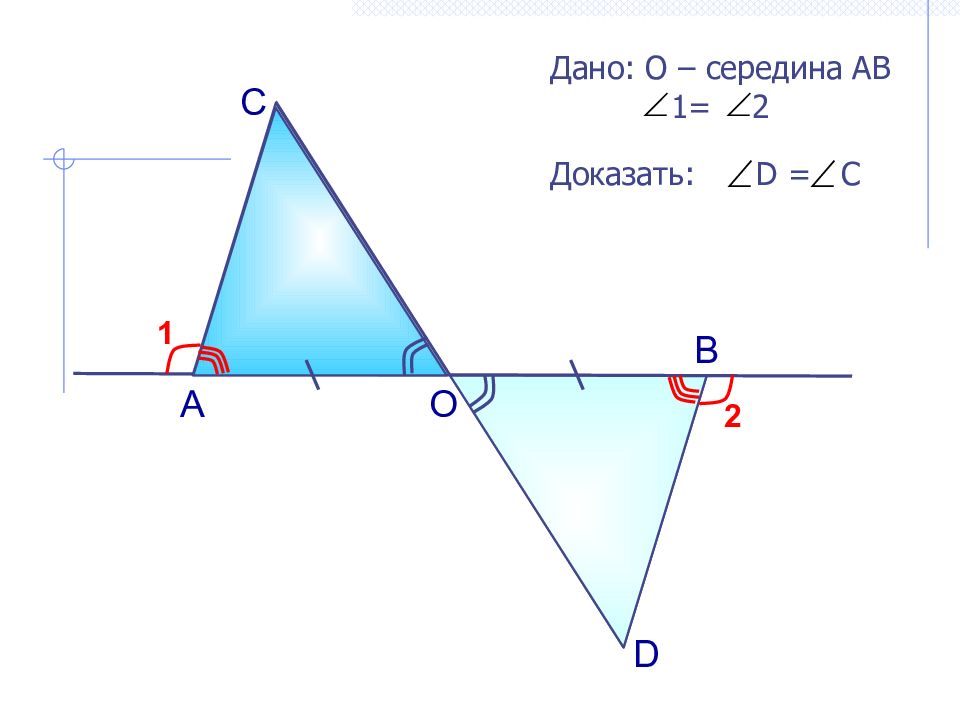
С H D Доказать: DCF = DEH F E Подсказка Вспомни свойство углов в равнобедренном треугольнике
K N A Доказать: KBA = NBC B Подсказка Определи вид треугольника АВС C
Доказать: АВС = А D М D М А В С
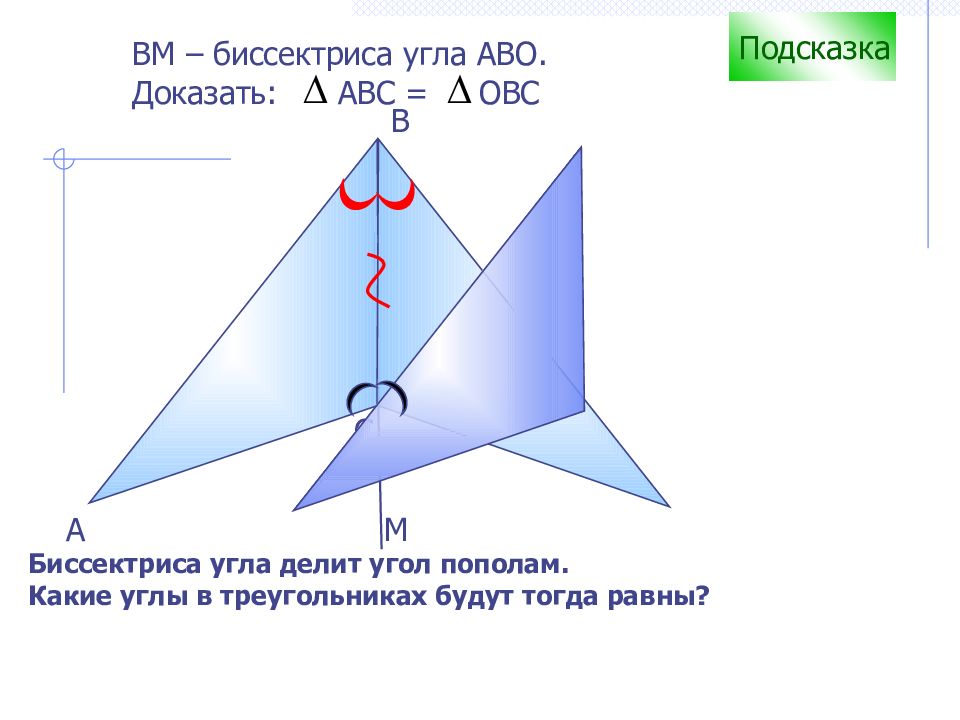
С B А В M – биссектриса угла АВО. Доказать: АВС = ОВС Подсказка Биссектриса угла делит угол пополам. Какие углы в треугольниках будут тогда равны? М
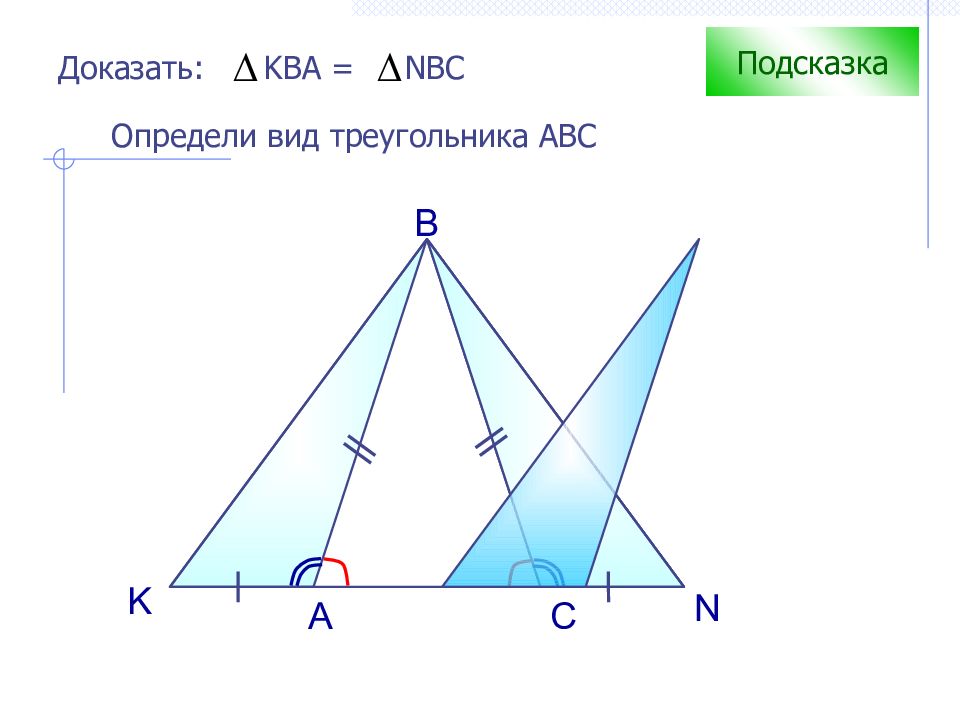
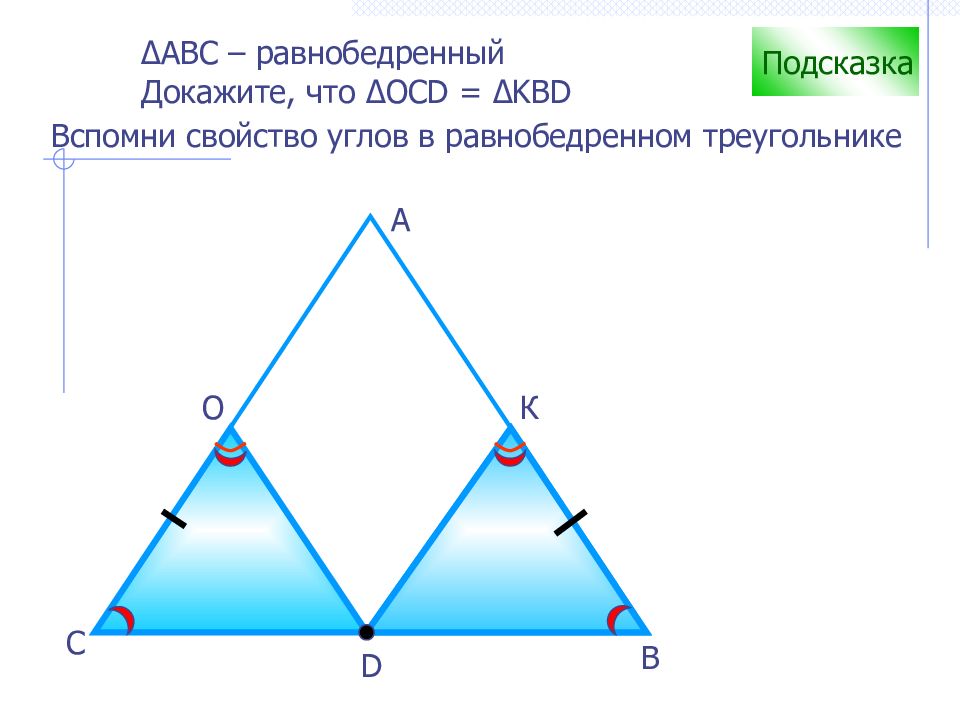
D В С А О К Подсказка Вспомни свойство углов в равнобедренном треугольнике ∆ АВС – равнобедренный Докажите, что ∆ OCD = ∆ KBD
А О В С D 1 2 Дано: О – середина АВ 1= 2 Доказать: D = C
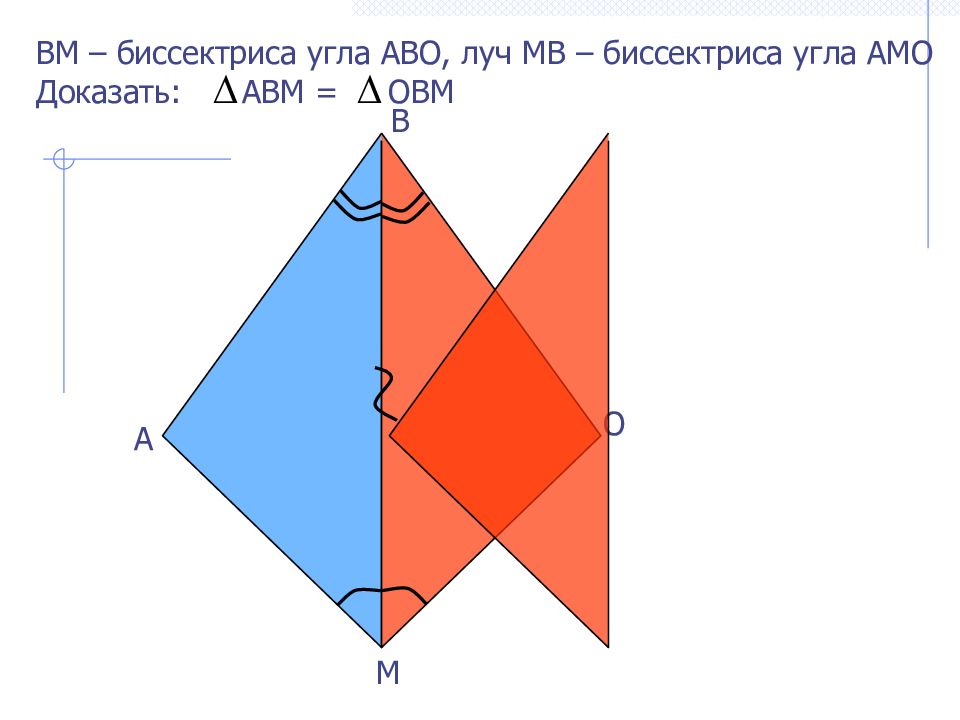
B А О В M – биссектриса угла АВО, луч МВ – биссектриса угла АМО Доказать: АВМ = ОВМ М
Дано: АВ = СВ, А = С Доказать: АМ = С N А B C M N
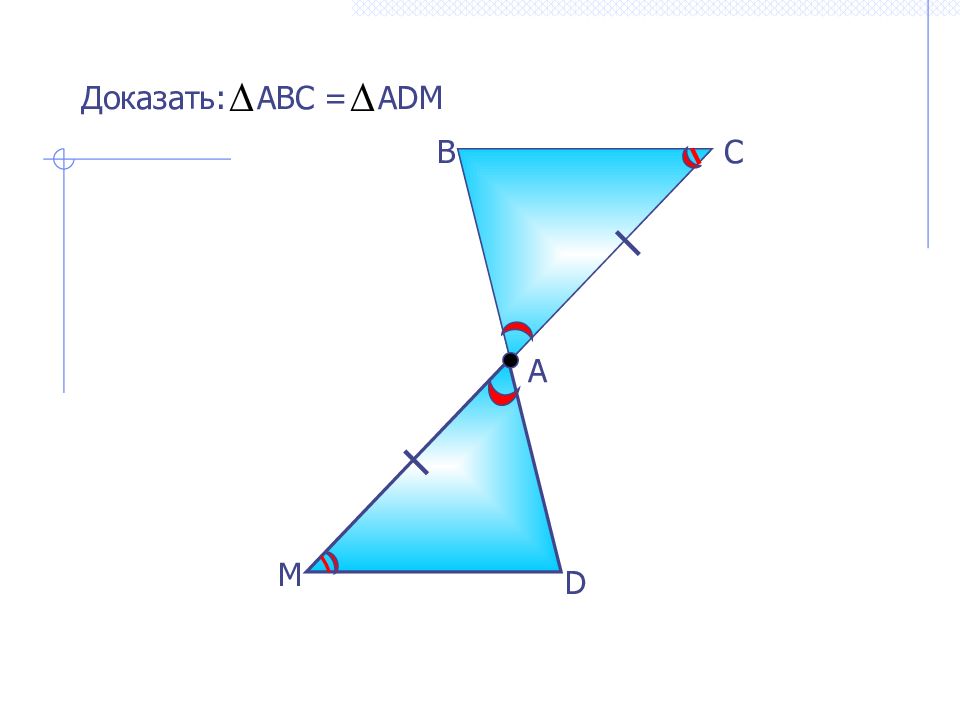
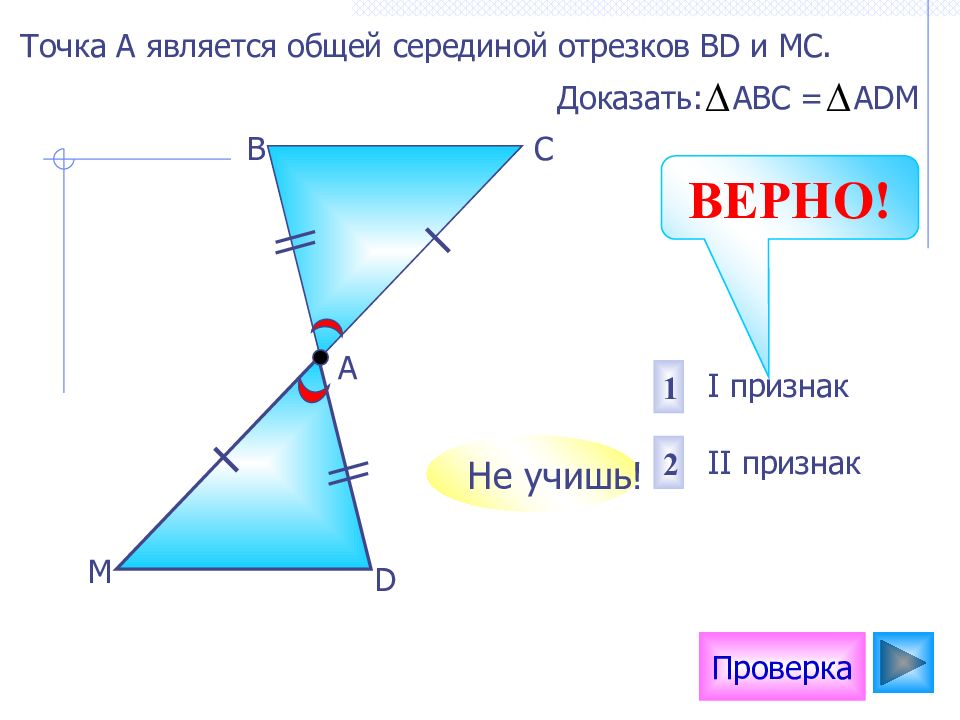
Проверка I признак II признак 2 1 Доказать: АВС = А D М D М А В С Не учишь! ВЕРНО! Точка А является общей серединой отрезков В D и МС.
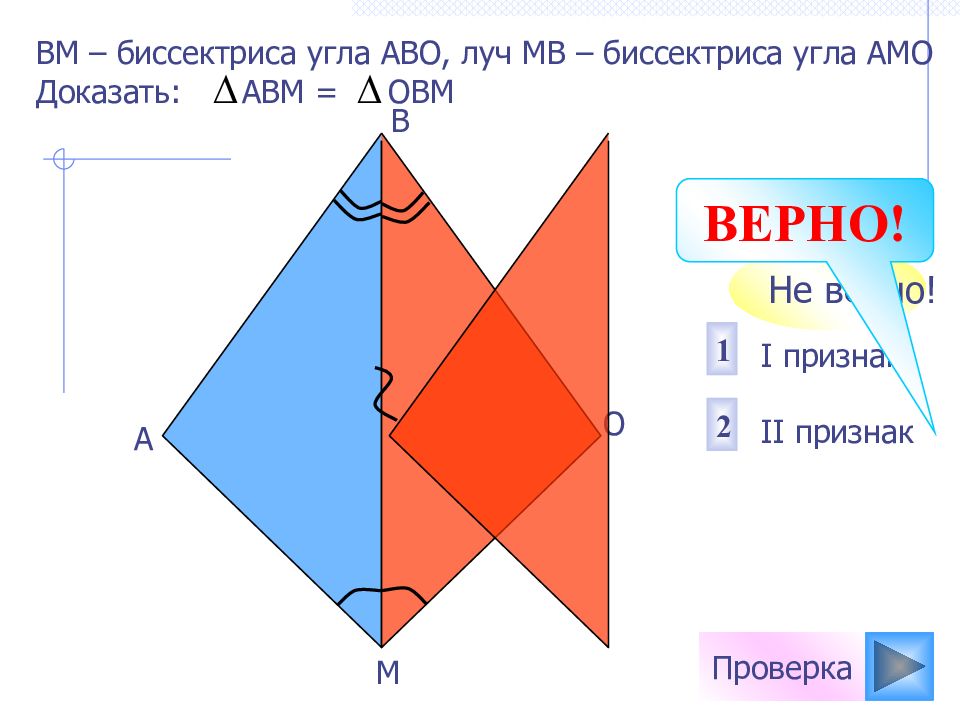
Проверка I признак II признак 1 2 Не верно! B А О В M – биссектриса угла АВО, луч МВ – биссектриса угла АМО Доказать: АВМ = ОВМ ВЕРНО! М
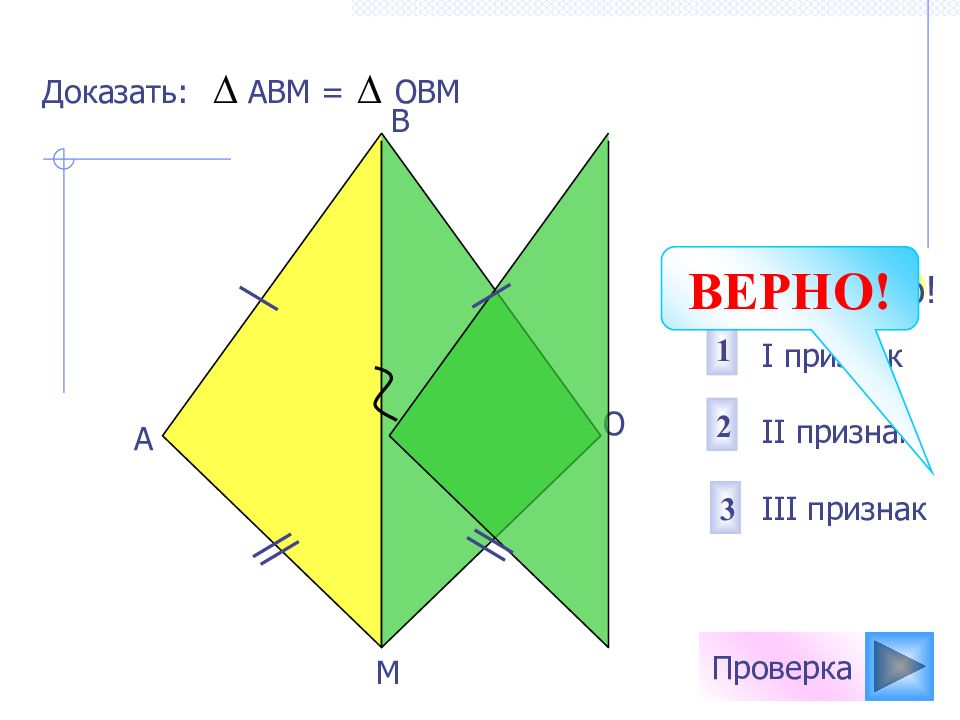
Проверка I признак II признак III признак 1 3 2 Не верно! B А О Доказать: АВМ = ОВМ ВЕРНО! М
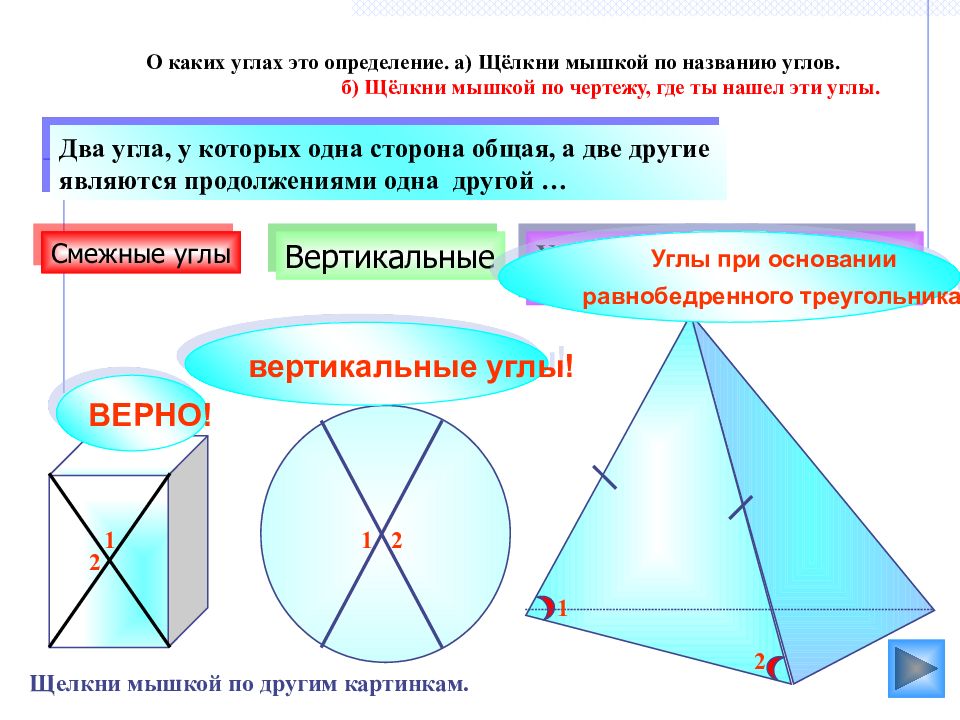
вертикальные углы! Вертикальные Углы при основании равнобедренного треугольника Два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой … Смежные углы 1 2 2 1 О каких углах это определение. а) Щёлкни мышкой по названию углов. б) Щёлкни мышкой по чертежу, где ты нашел эти углы. 1 2 ВЕРНО! Углы при основании равнобедренного треугольника ! Щелкни мышкой по другим картинкам.
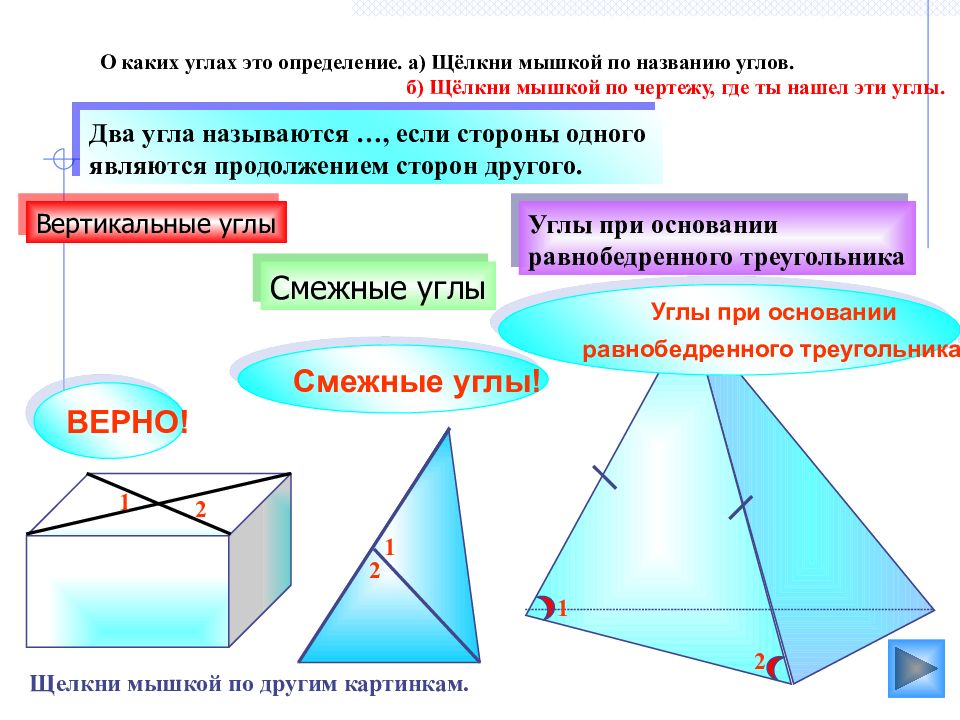
Смежные углы Углы при основании равнобедренного треугольника Два угла называются …, если стороны одного являются продолжением сторон другого. Вертикальные углы 1 2 2 1 О каких углах это определение. а) Щёлкни мышкой по названию углов. б) Щёлкни мышкой по чертежу, где ты нашел эти углы. 1 2 ВЕРНО! Смежные углы! Углы при основании равнобедренного треугольника ! Щелкни мышкой по другим картинкам.
