Первый слайд презентации: Углы, связанные с окружностью
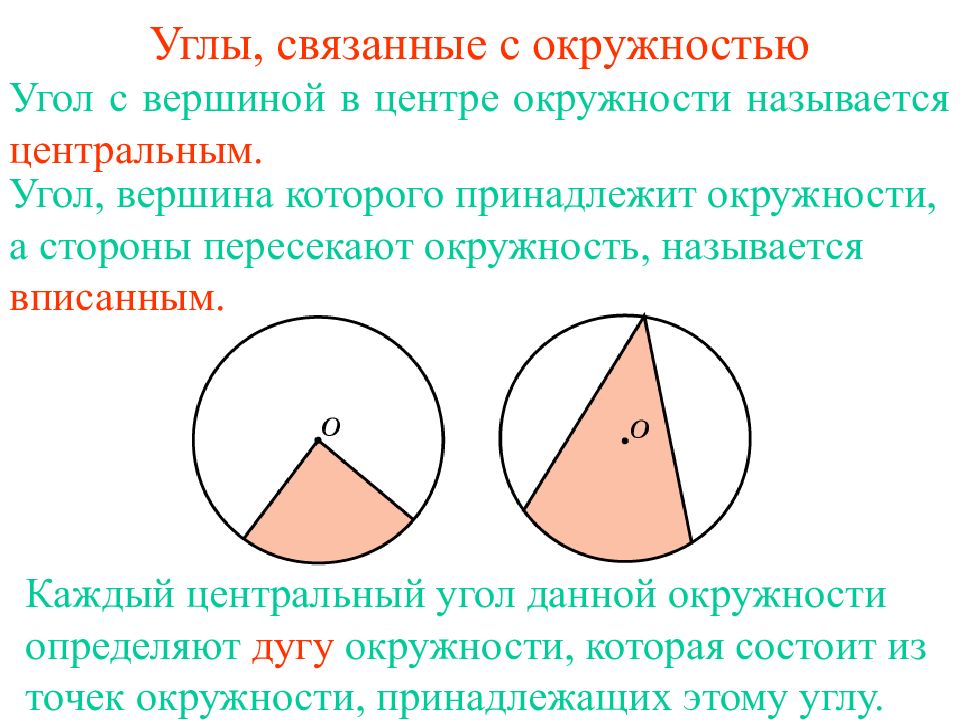
Угол с вершиной в центре окружности называется центральным. Угол, вершина которого принадлежит окружности, а стороны пересекают окружность, называется вписанным. Каждый центральный уг ол данной окружности определяют дуг у окружности, котор ая состо и т из точек окружности, принадлежащих эт ому угл у.
Слайд 2: Вписанный угол
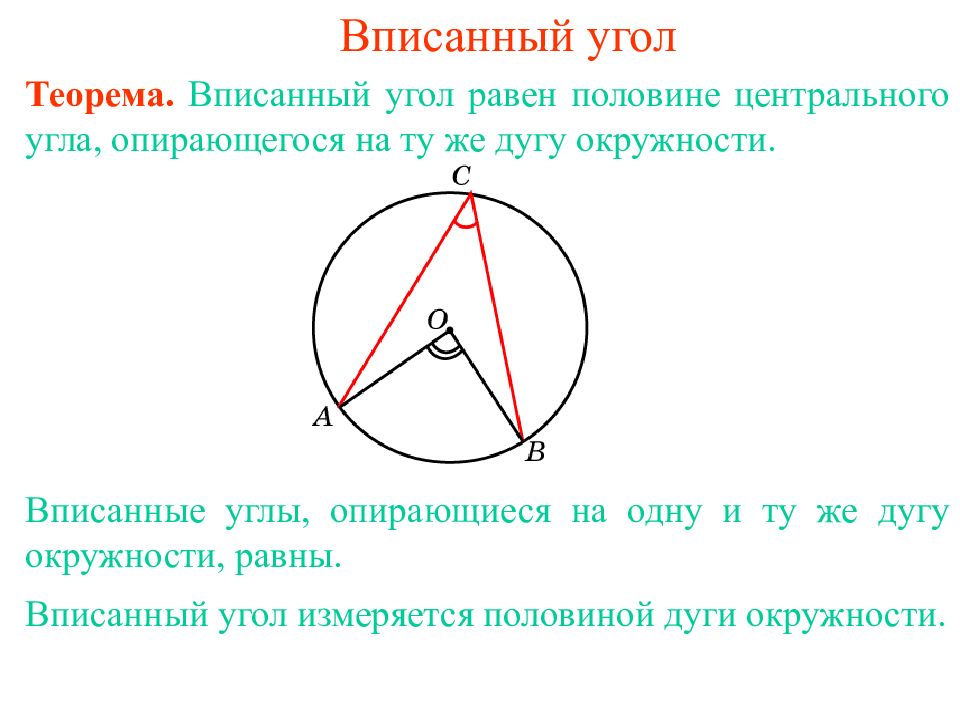
Теорема. Вписанный угол равен половине центрального угла, опирающегося на ту же дугу окружности. Вписанны й уг ол измеряется половиной дуги окружности. Вписанные углы, опирающиеся на одну и ту же дугу окружности, равны.
Слайд 3: Угол между касательной и хордой
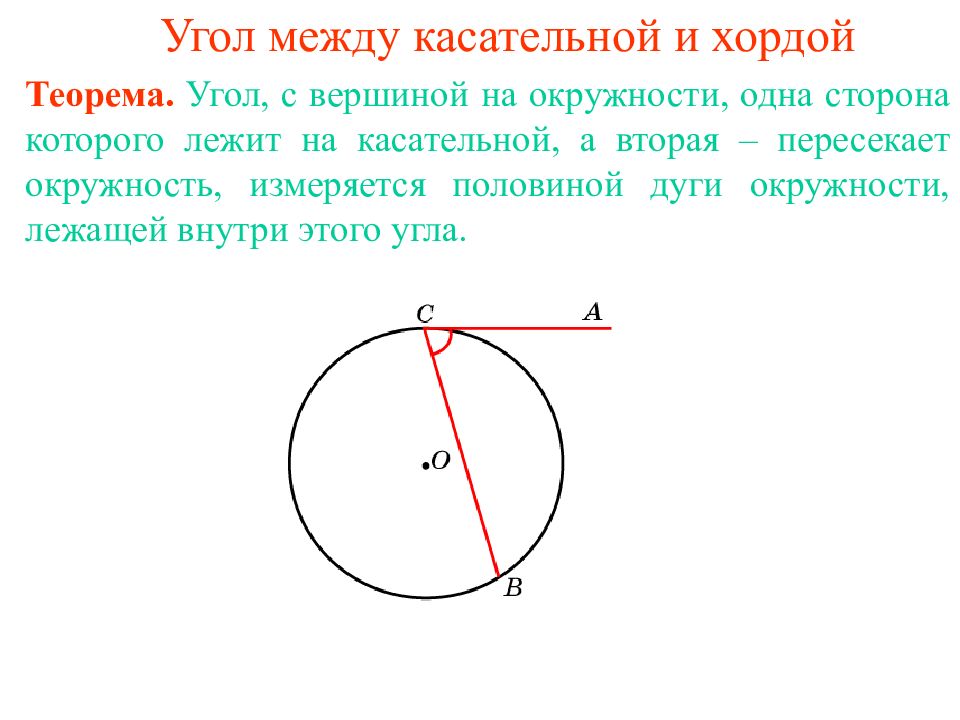
Теорема. Угол, с вершиной на окружности, одна сторона которого лежит на касательной, а вторая – пересекает окружность, измеряется половиной дуги окружности, лежащей внутри этого угла.
Слайд 4: Угол с вершиной внутри окружности
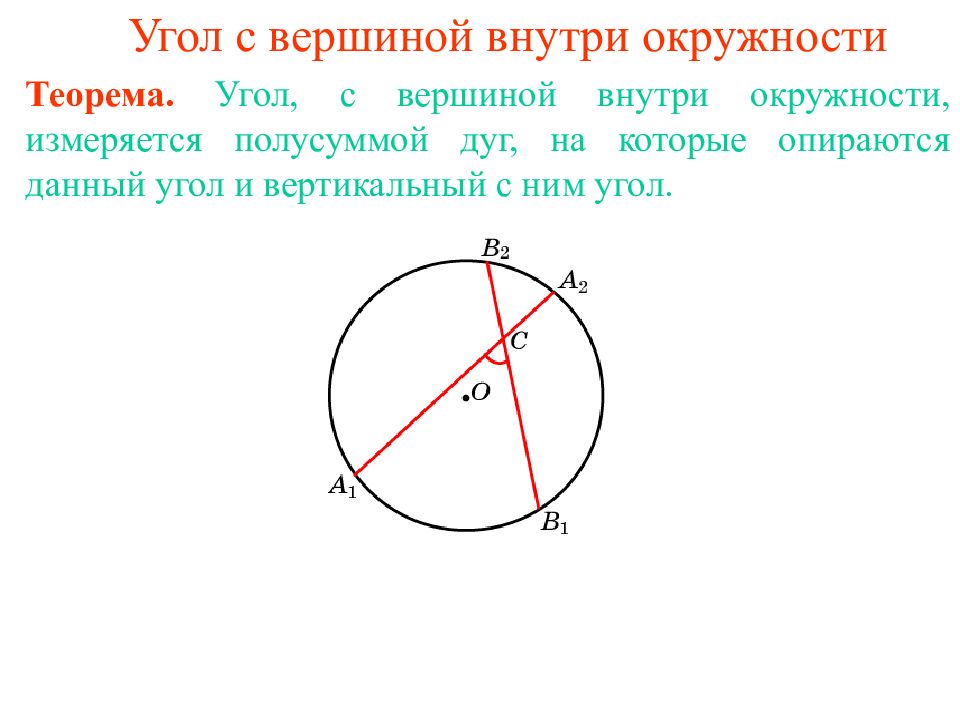
Теорема. Угол, с вершиной внутри окружности, измеряется полусуммой дуг, на которые опираются данный угол и вертикальный с ним угол.
Слайд 5: Угол с вершиной вне окружности
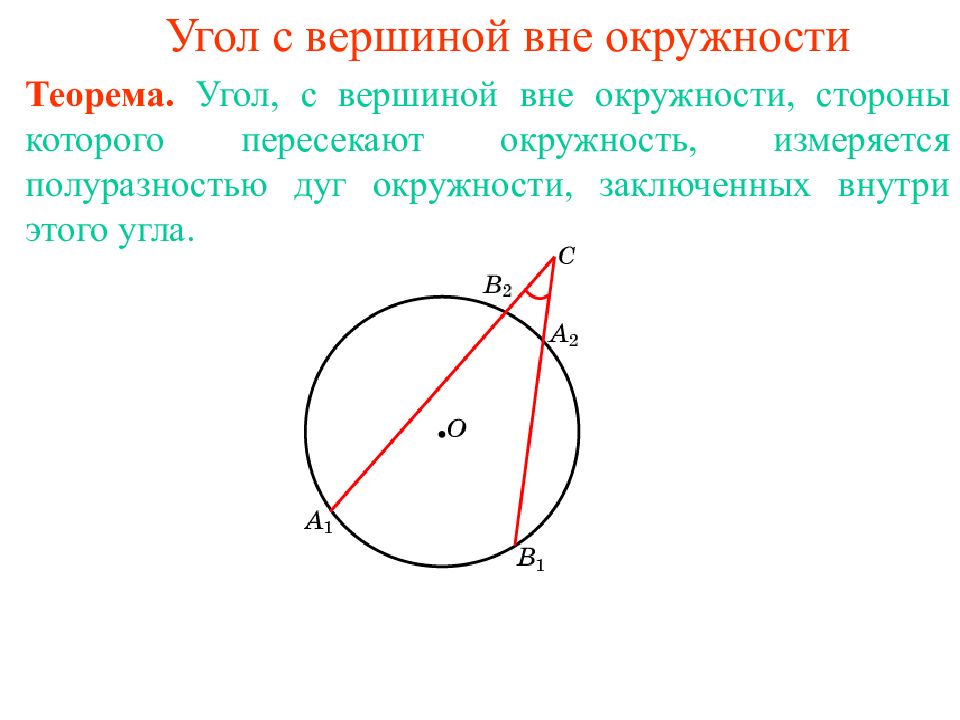
Теорема. Угол, с вершиной вн е окружности, стороны которого пересекают окружность, измеряется полу разностью дуг окружности, заключенных внутри этого угла.
Слайд 6: Угол с вершиной вне окружности
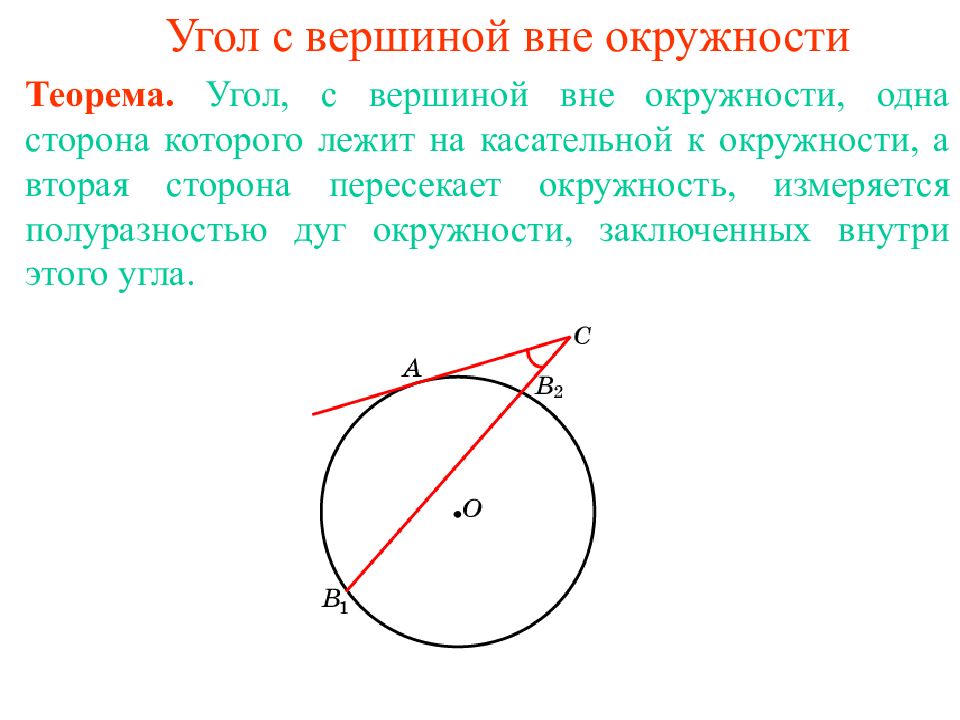
Теорема. Угол, с вершиной вн е окружности, одна сторона которого лежит на касательной к окружности, а вторая сторона пересекает окружность, измеряется полу разностью дуг окружности, заключенных внутри этого угла.
Слайд 7: Угол с вершиной вне окружности
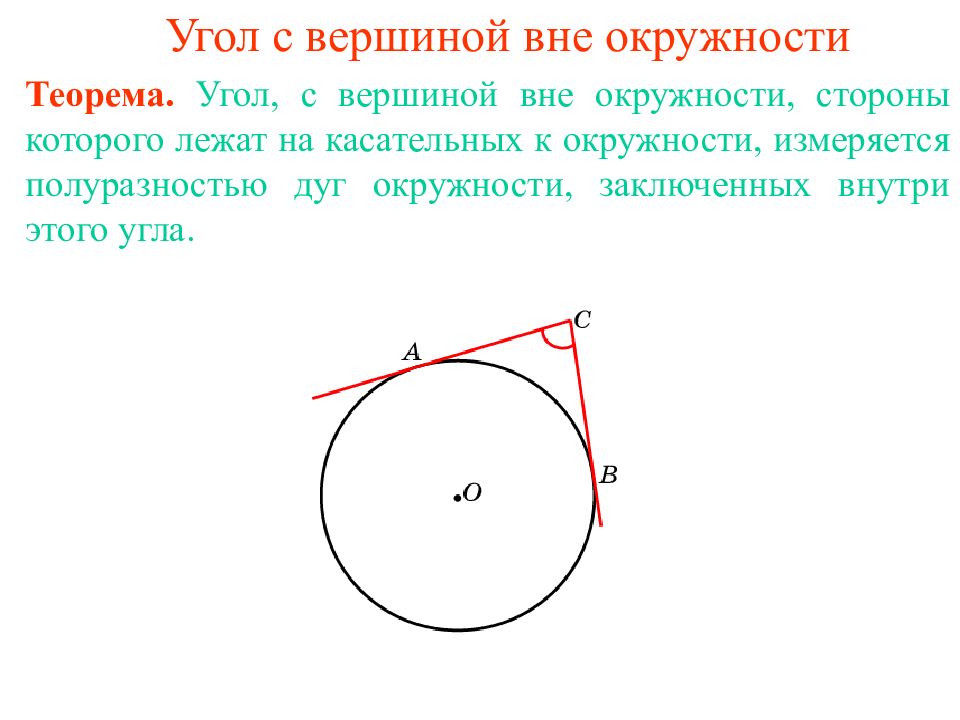
Теорема. Угол, с вершиной вн е окружности, стороны которого лежат на касательных к окружности, измеряется полу разностью дуг окружности, заключенных внутри этого угла.
Слайд 8: Упражнение 1
Чему равен вписанный угол, опирающийся на диаметр окружности? Ответ: 90 о.
Слайд 9: Упражнение 2
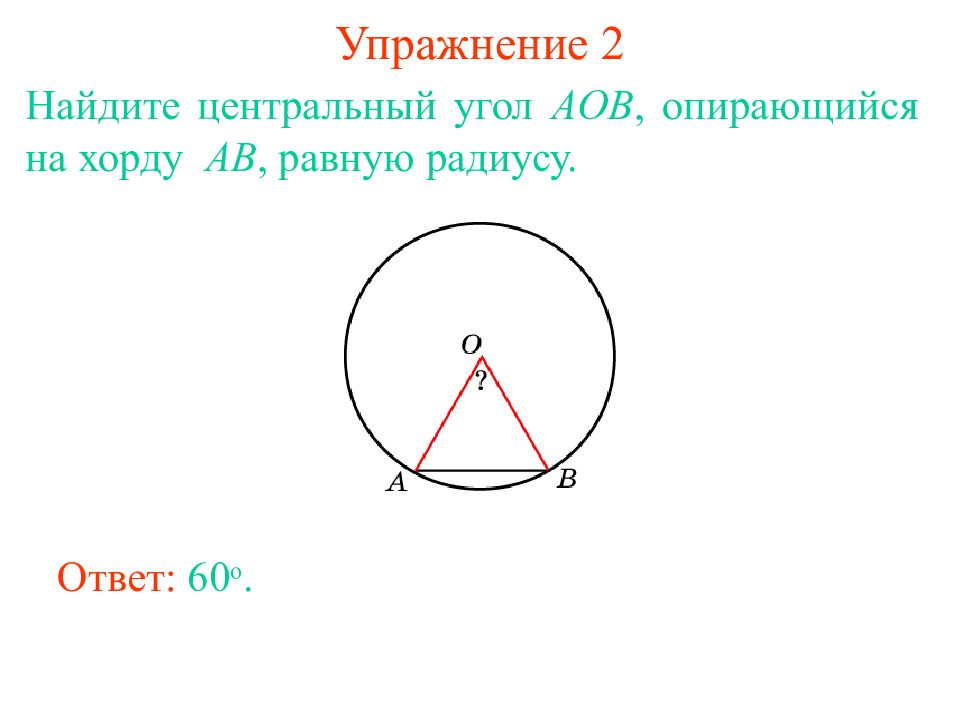
Найдите центральный угол AOB, опирающийся на хорду AB, равную радиусу. Ответ: 6 0 о.
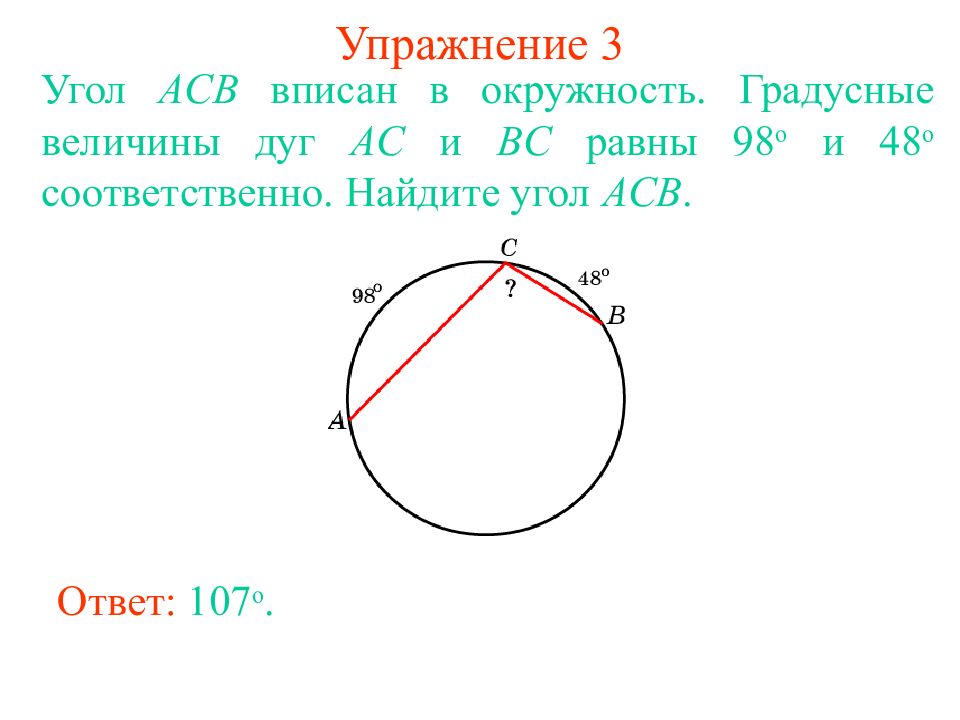
Слайд 10: Упражнение 3
Угол ACB вписан в окружность. Градусные величины дуг AC и BC равны 98 о и 48 о соответственно. Найдите угол ACB. Ответ: 107 о.
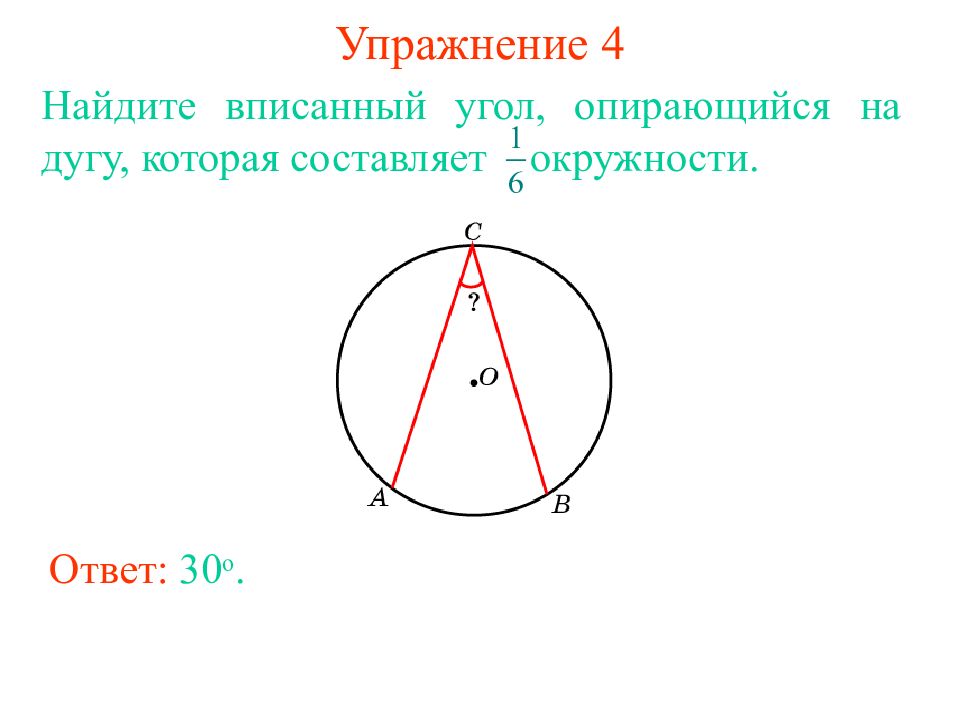
Слайд 11: Упражнение 4
Ответ: 30 о. Найдите вписанный угол, опирающийся на дугу, которая составляет окружности.
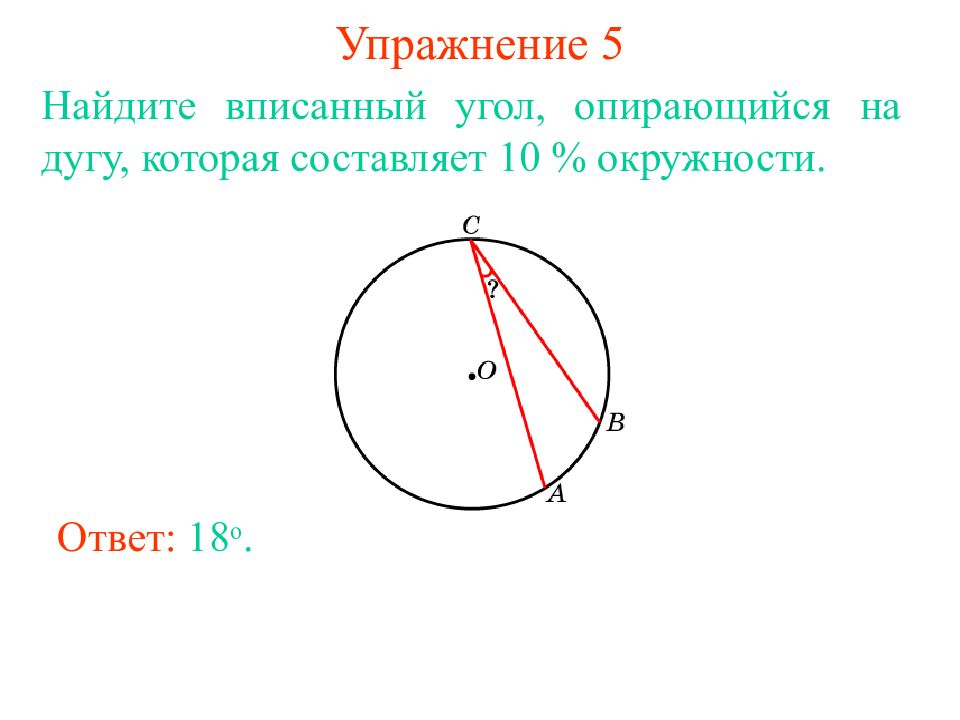
Слайд 12: Упражнение 5
Ответ: 18 о. Найдите вписанный угол, опирающийся на дугу, которая составляет 10 % окружности.
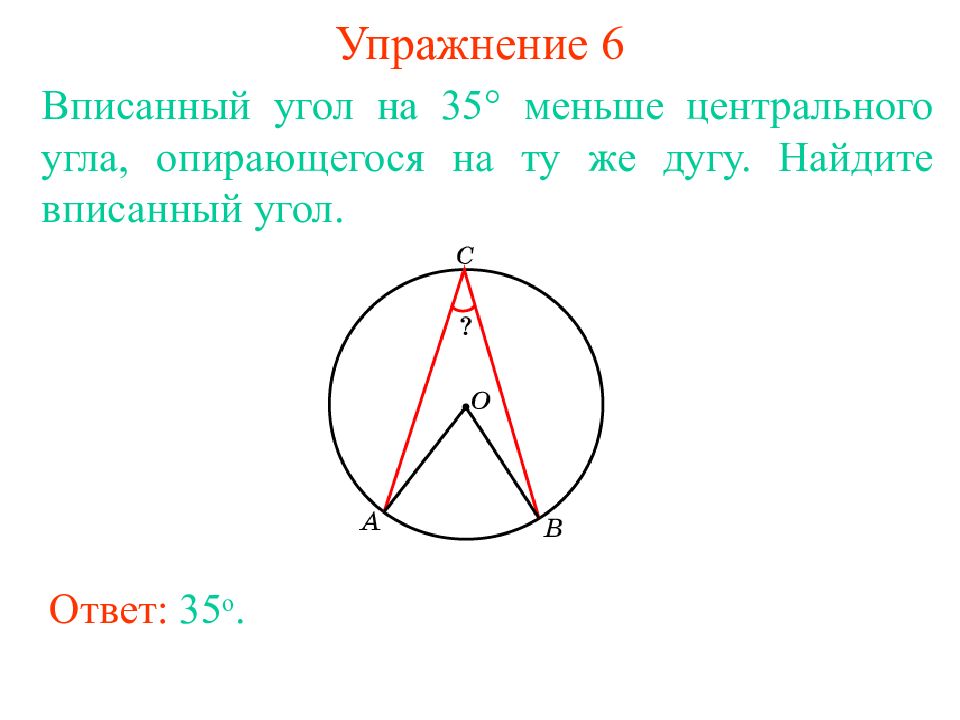
Слайд 13: Упражнение 6
Вписанный угол на 35 меньше центрального угла, опирающегося на ту же дугу. Найдите вписанный уг ол. Ответ: 35 о.
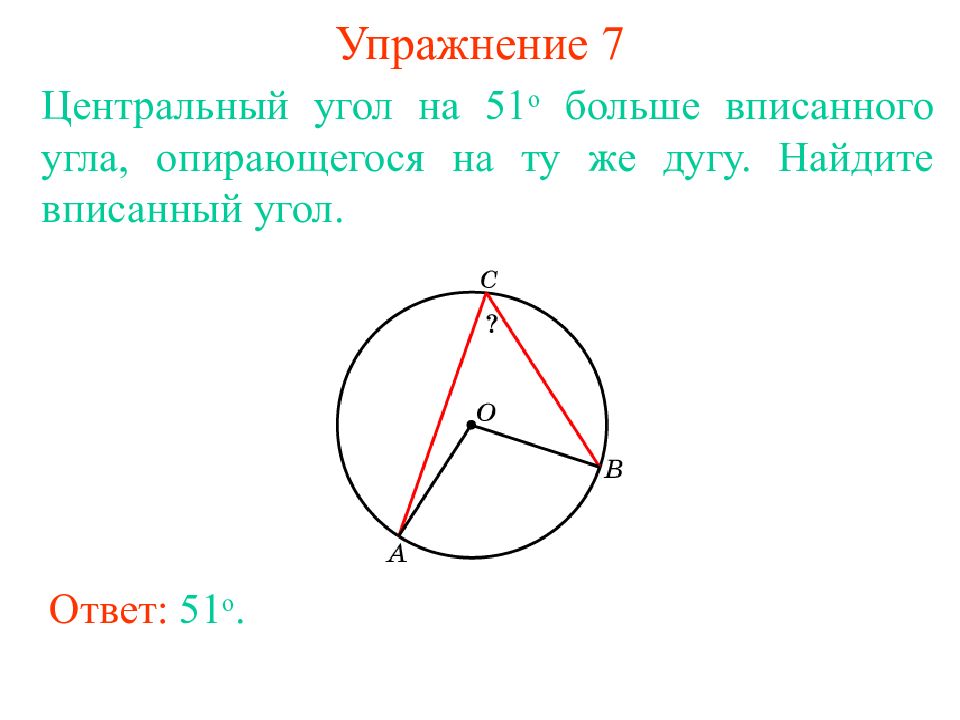
Слайд 14: Упражнение 7
Центральный угол на 51 о больше вписанного угла, опирающегося на ту же дугу. Найдите вписанный уг ол. Ответ: 51 о.
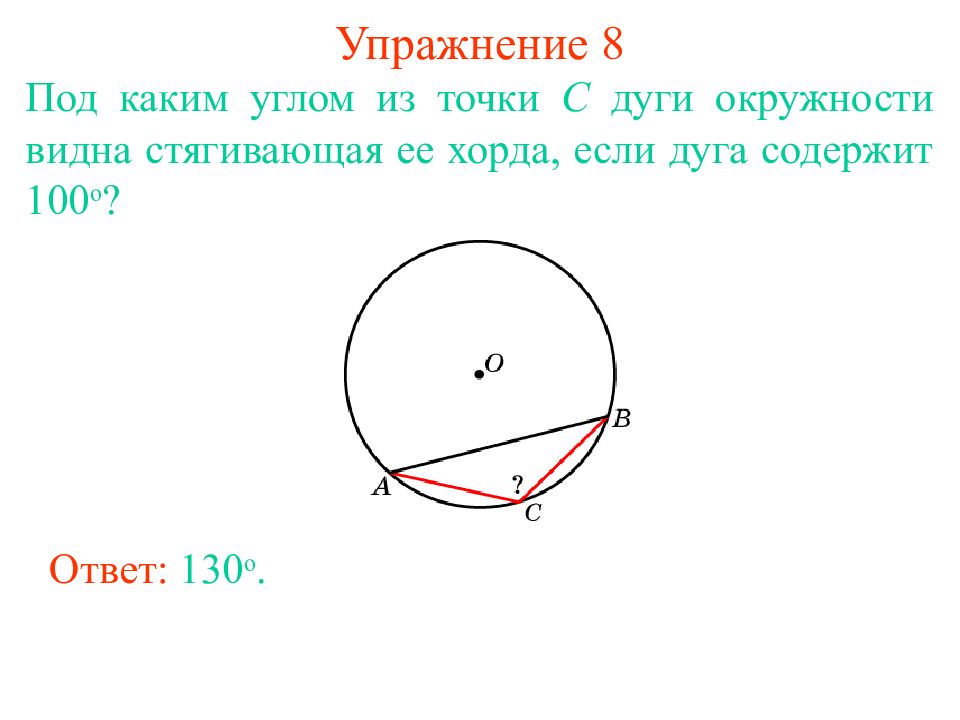
Слайд 15: Упражнение 8
Под каким углом из точки C дуги окружности видна стягивающая ее хорда, если дуга содержит 100 о ? Ответ: 13 0 о.
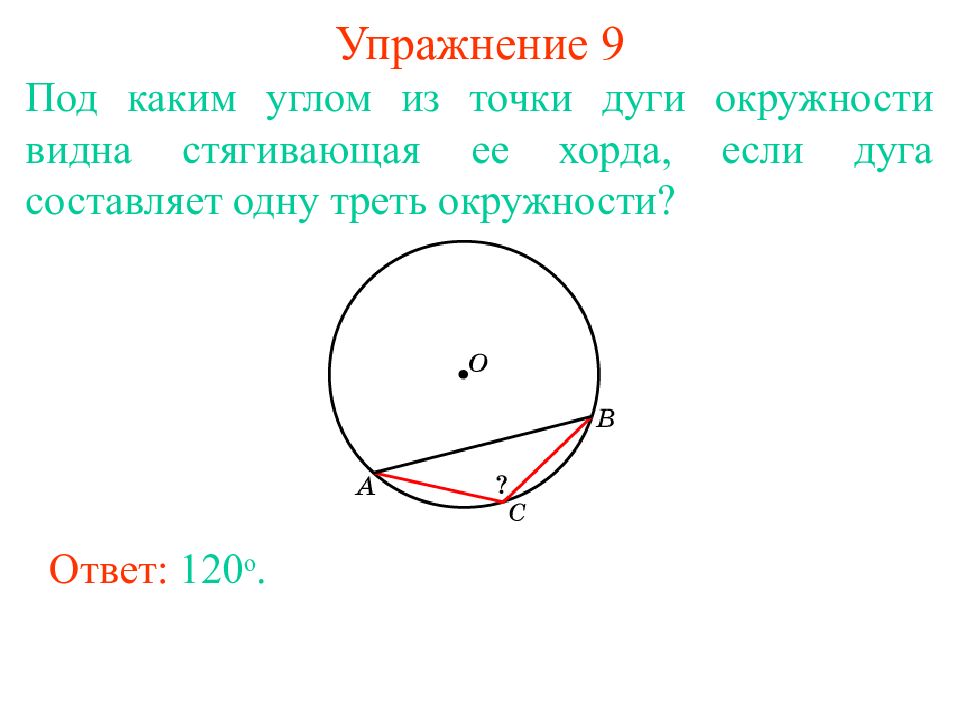
Слайд 16: Упражнение 9
Под каким углом из точки дуги окружности видна стягивающая ее хорда, если дуга составляет одну треть окружности ? Ответ: 12 0 о.
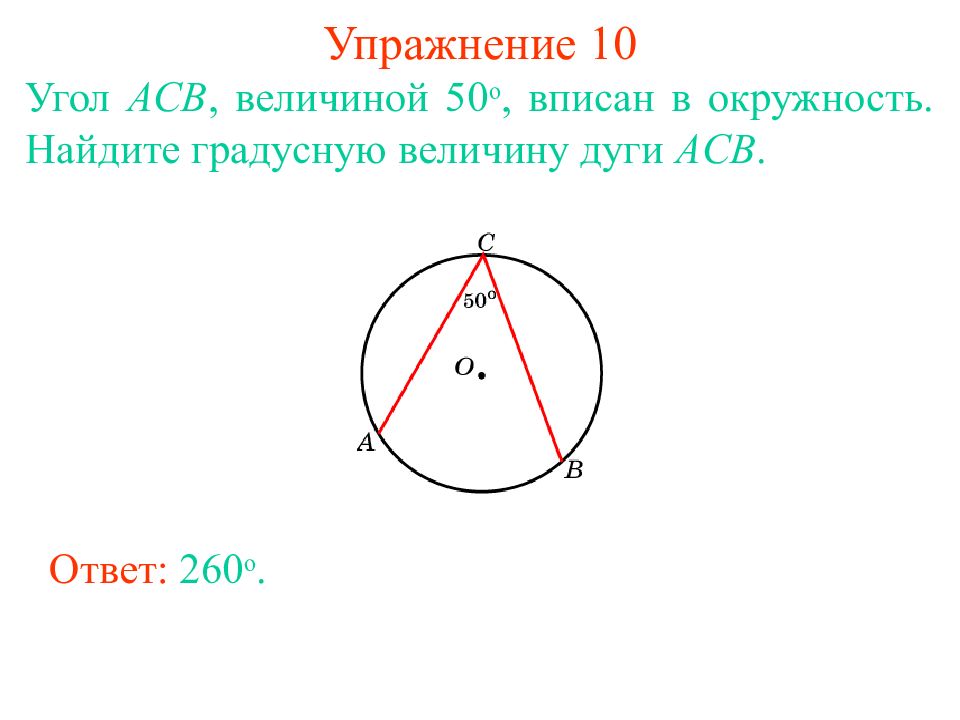
Слайд 17: Упражнение 1 0
Угол ACB, величиной 50 о, вписан в окружность. Найдите градусную величину дуги ACB. Ответ: 260 о.
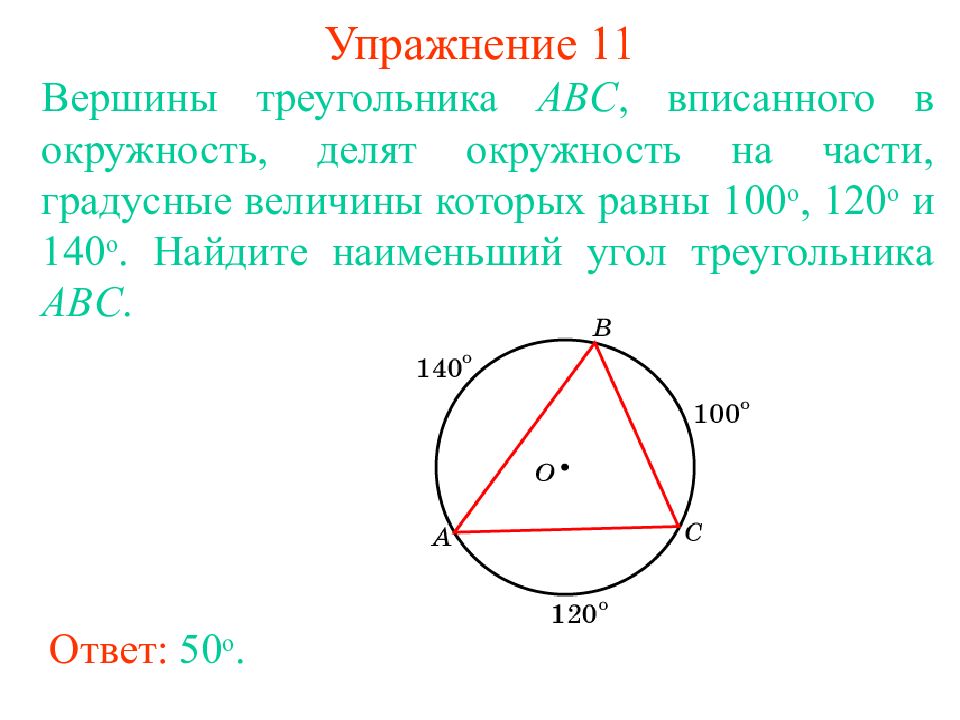
Слайд 18: Упражнение 11
Ответ: 5 0 о. Вершины треугольника ABC, вписанного в окружность, делят окружность на части, градусные величины которых равны 100 о, 120 о и 140 о. Найдите наименьший угол треугольника ABC.
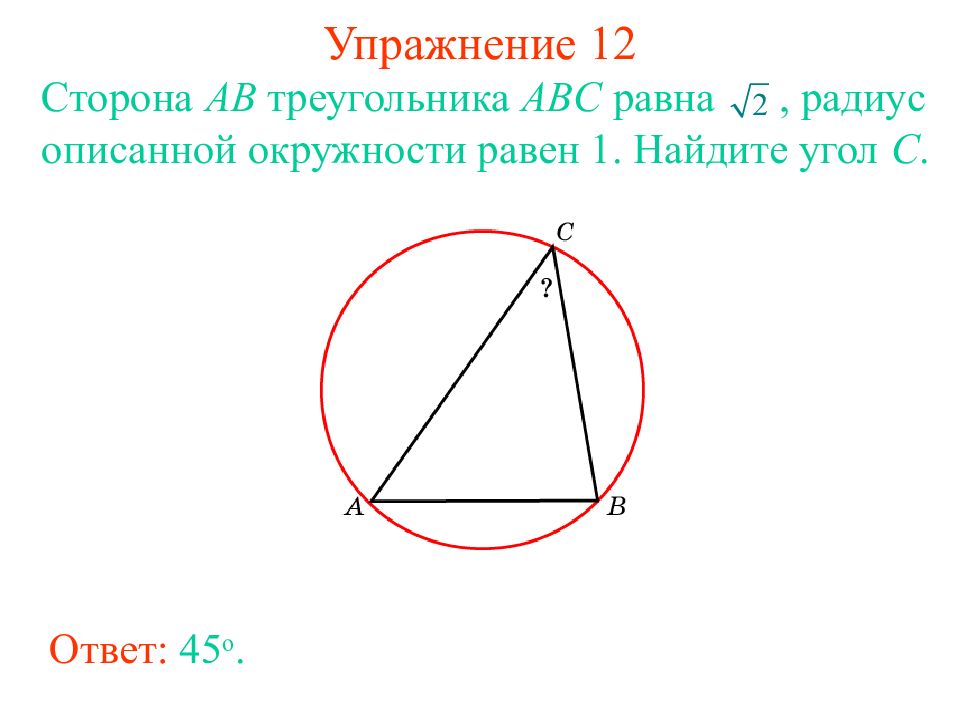
Слайд 19: Упражнение 12
Ответ: 45 о. Сторона AB треугольника ABC равна, радиус описанной окружности равен 1. Найдите угол C.
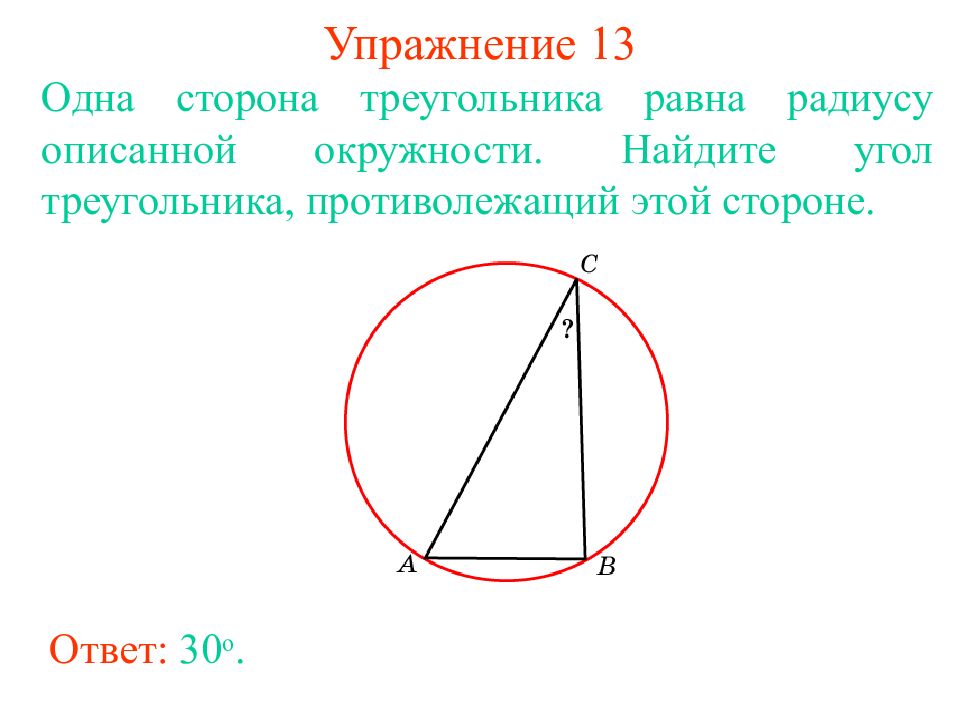
Слайд 20: Упражнение 1 3
Ответ: 30 о. Одна сторона треугольника равна радиусу описанной окружности. Найдите угол треугольника, противолежащий этой стороне.
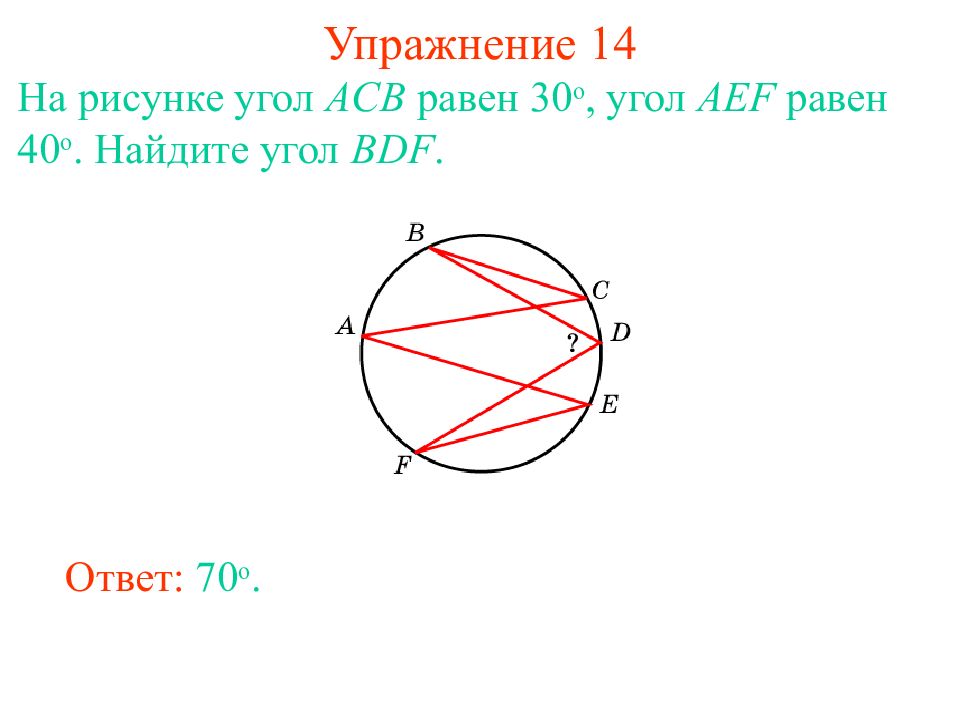
Слайд 21: Упражнение 14
На рисунке угол ACB равен 30 о, угол AEF равен 40 о. Найдите угол BDF. Ответ: 70 о.
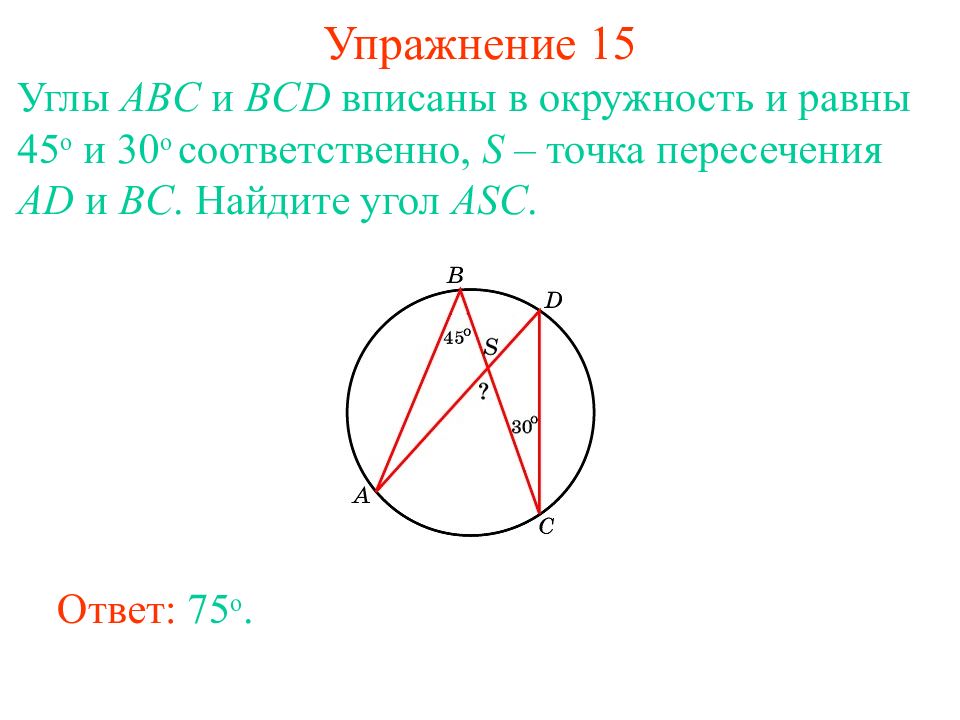
Слайд 22: Упражнение 1 5
Углы ABC и BCD вписаны в окружность и равны 45 о и 30 о соответственно, S – точка пересечения AD и BC. Найдите угол ASC. Ответ: 75 о.
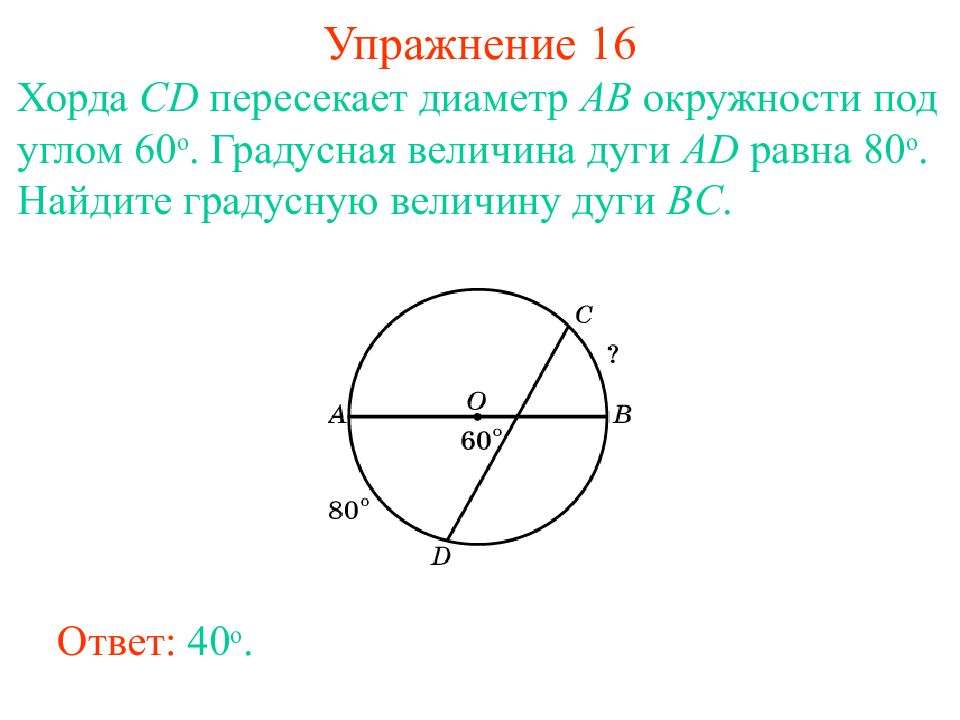
Слайд 23: Упражнение 1 6
Хорда CD пересекает диаметр AB окружности под углом 60 о. Градусная величина дуги AD равна 80 о. Найдите градусную величину дуги BC. Ответ: 4 0 о.
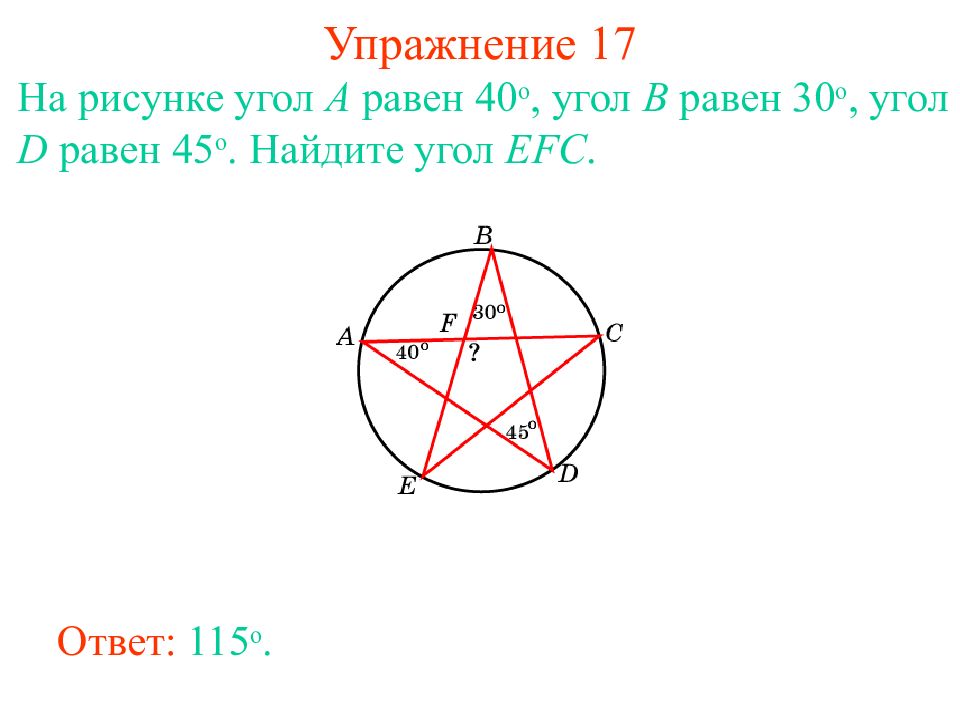
Слайд 24: Упражнение 1 7
На рисунке угол A равен 4 0 о, угол B равен 3 0 о, угол D равен 45 о. Найдите угол EFC. Ответ: 115 о.
Слайд 25: Упражнение 1 8
Стороны угла с вершиной C вне окружности отсекают от окружности дуги A 1 B 1, A 2 B 2, градусные величины которых равны 30 о и 1 0 0 о. Найдите угол C. Ответ: 35 о.
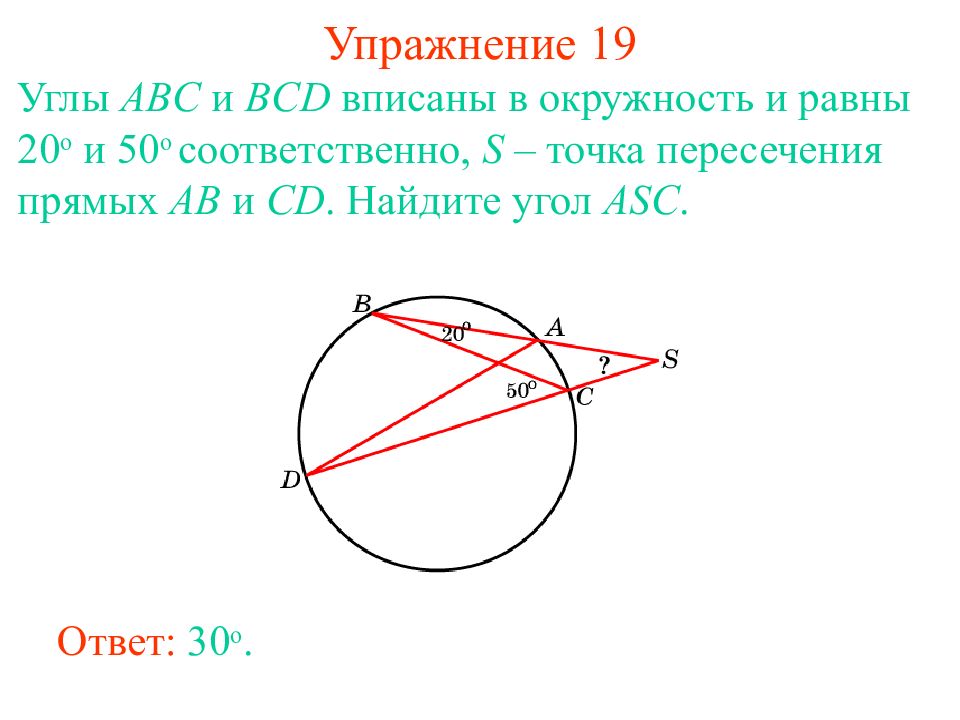
Слайд 26: Упражнение 1 9
Углы ABC и BCD вписаны в окружность и равны 20 о и 5 0 о соответственно, S – точка пересечения прямых AB и CD. Найдите угол ASC. Ответ: 30 о.
Слайд 27: Упражнение 20
Стороны угла с вершиной C вне окружности отсекают от окружности дуги AB 1, AB 2, градусные величины которых равны 6 0 о и 1 4 0 о соответственно, CA – касательная. Найдите угол C. Ответ: 40 о.
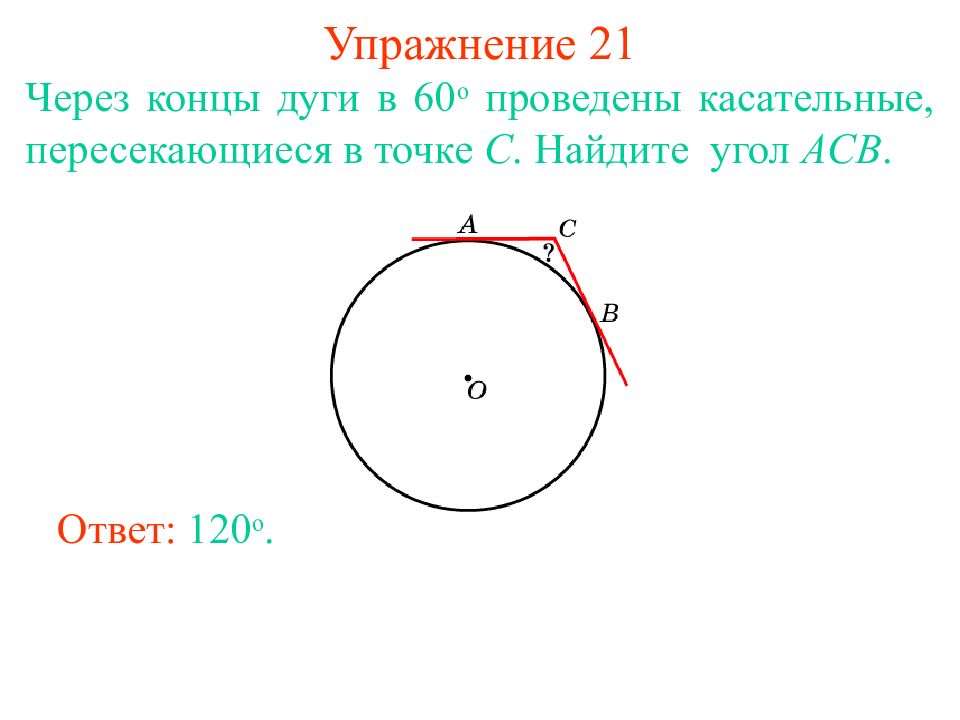
Слайд 28: Упражнение 21
Через концы дуги в 60 о проведены касательные, пересекающиеся в точке C. Найдите угол ACB. Ответ: 120 о.
Слайд 29: Упражнение 2 2
Хорда АВ стягивает дугу окружности в 44 о. Найдите углы, которые образует эта хорда с касательными к окружности, проведенными через ее концы. Ответ: 22 о.
Слайд 30: Упражнение 2 3
Две равные окружности расположены таким образом, что каждая из них проходит через центр другой. Найдите уг ол, под которым видна их общая хорда AB из центра O 1 одной из окружностей. Ответ: 12 0 о.
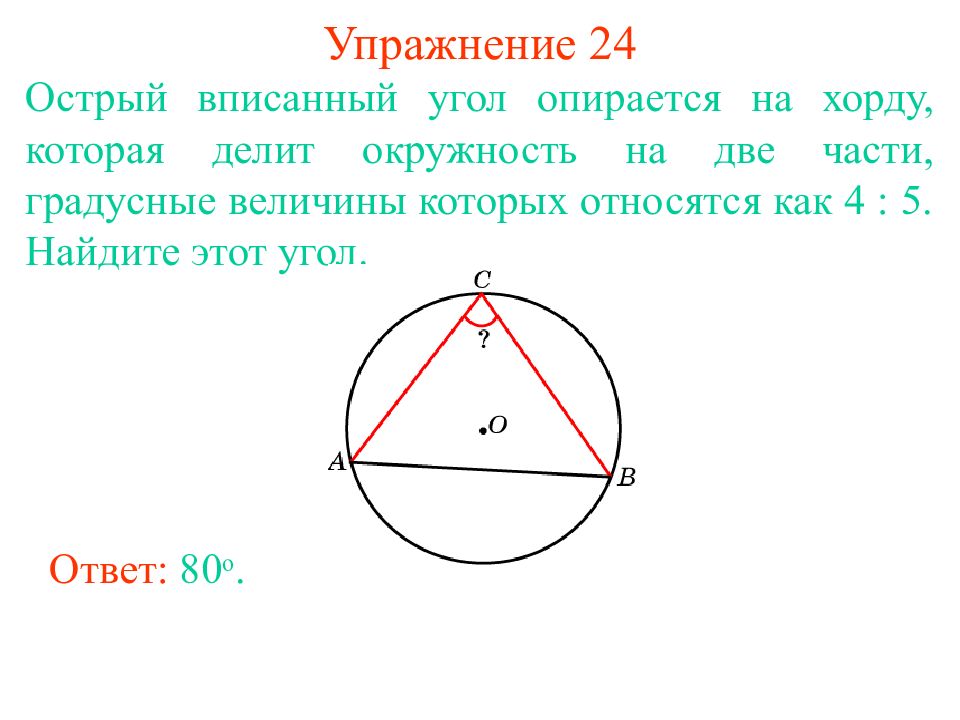
Слайд 31: Упражнение 2 4
Острый вписанный угол опирается на хорду, которая делит окружность на две части, градусные величины которых относятся как 4 : 5. Найдите этот угол. Ответ: 80 о.
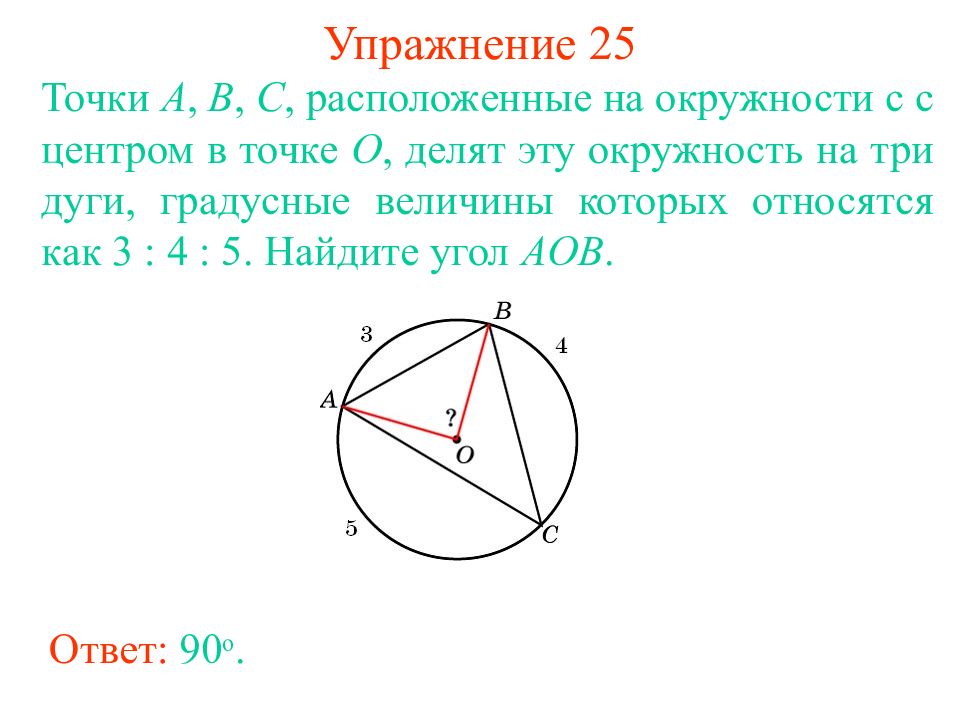
Слайд 32: Упражнение 2 5
Ответ: 90 о. Точки А, В, С, расположенные на окружности c с центром в точке O, делят эту окружность на три дуги, градусные величины которых относятся как 3 : 4 : 5. Найдите уг ол AOB.
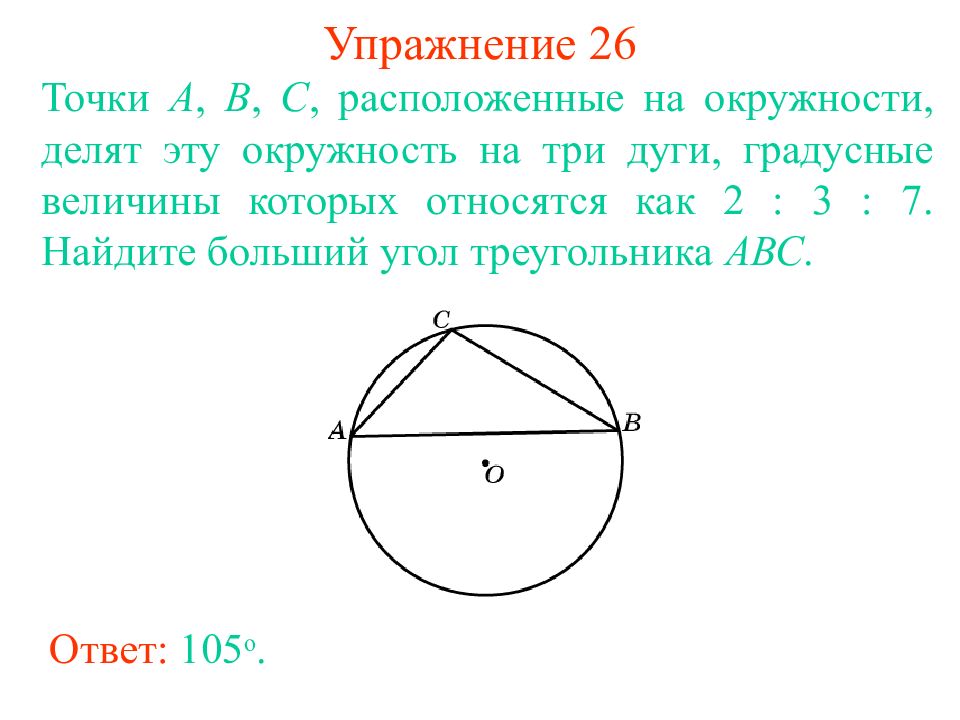
Слайд 33: Упражнение 2 6
Ответ: 105 о. Точки А, В, С, расположенные на окружности, делят эту окружность на три дуги, градусные величины которых относятся как 2 : 3 : 7. Найдите больший уг ол треугольника АВС.
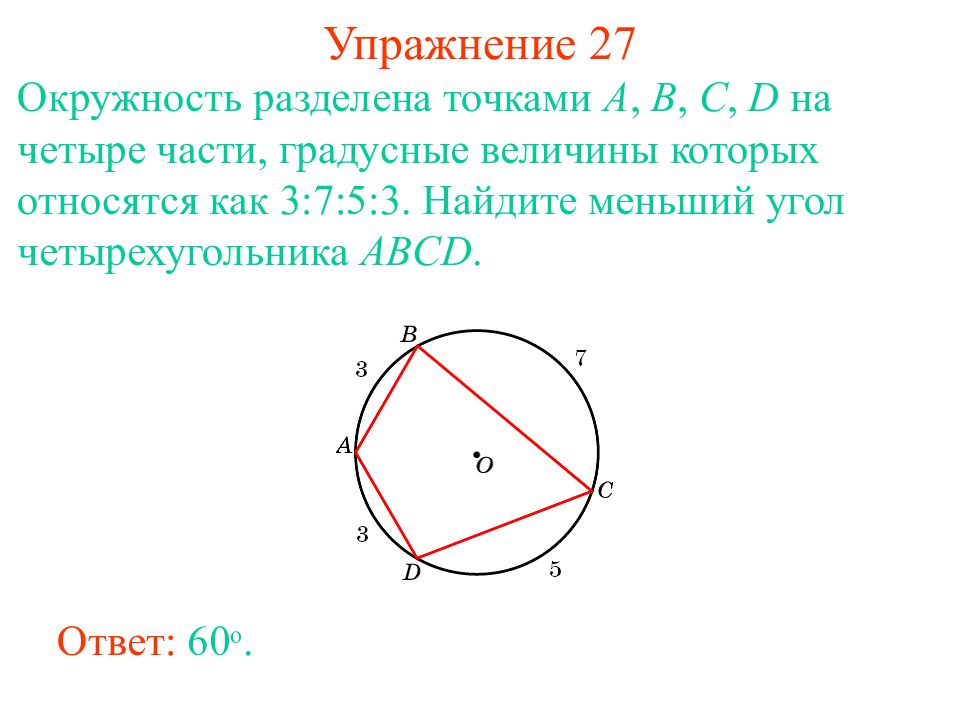
Слайд 34: Упражнение 2 7
Окружность разделена точками A, B, C, D на четыре части, градусные величины которых относятся как 3:7:5:3. Найдите меньший уг ол четырех угольника ABCD. Ответ: 60 о.
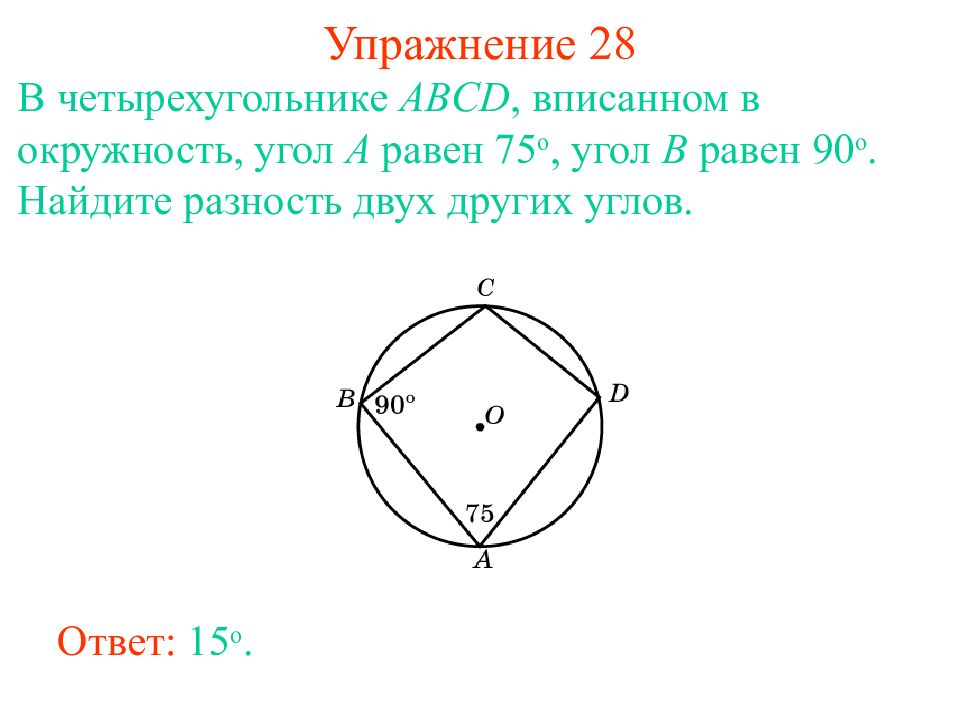
Слайд 35: Упражнение 2 8
В четырехугольнике ABCD, вписанном в окружность, угол A равен 75 о, угол B равен 90 о. Найдите разность двух других углов. Ответ: 15 о.
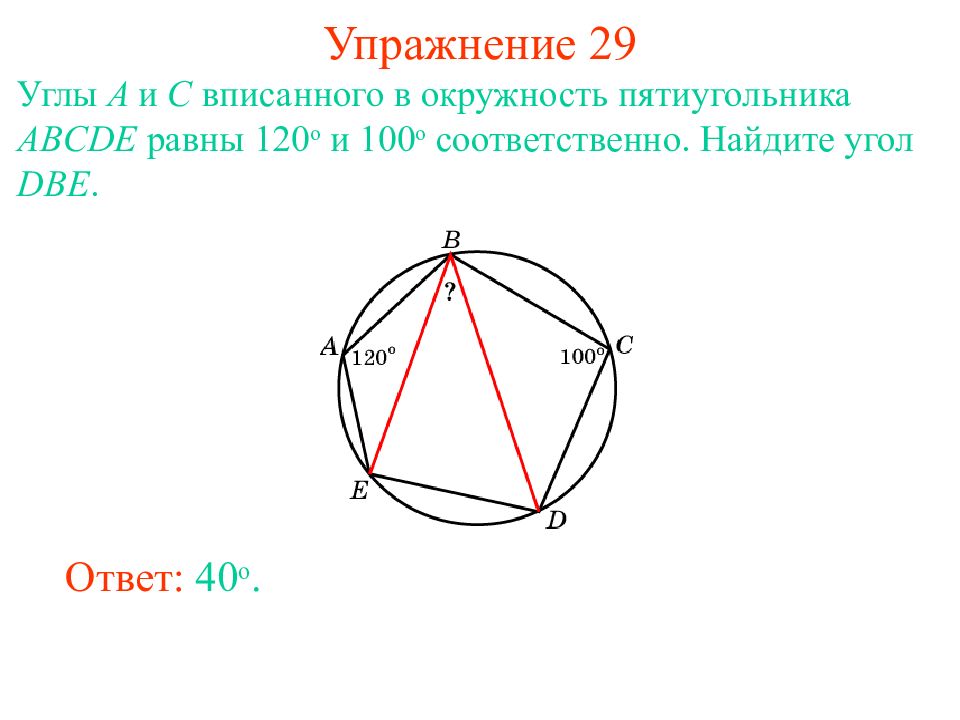
Слайд 36: Упражнение 2 9
Углы A и C вписанного в окружность пятиугольника ABCDE равны 120 о и 100 о соответственно. Найдите угол DBE. Ответ: 40 о.
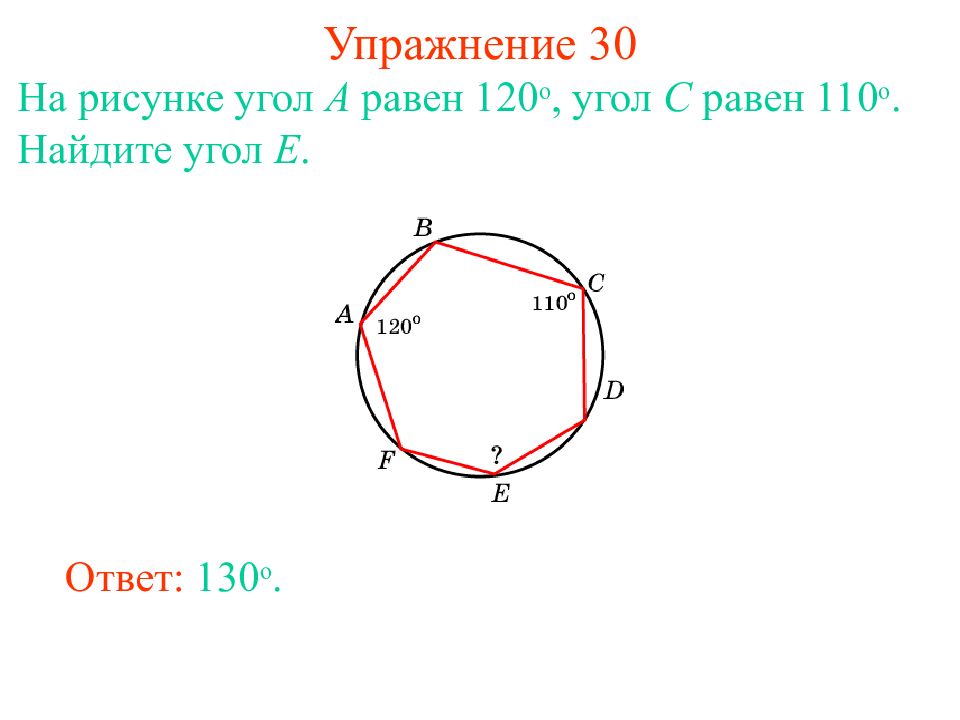
Слайд 37: Упражнение 30
На рисунке угол A равен 12 0 о, угол C равен 11 0 о. Найдите угол E. Ответ: 130 о.
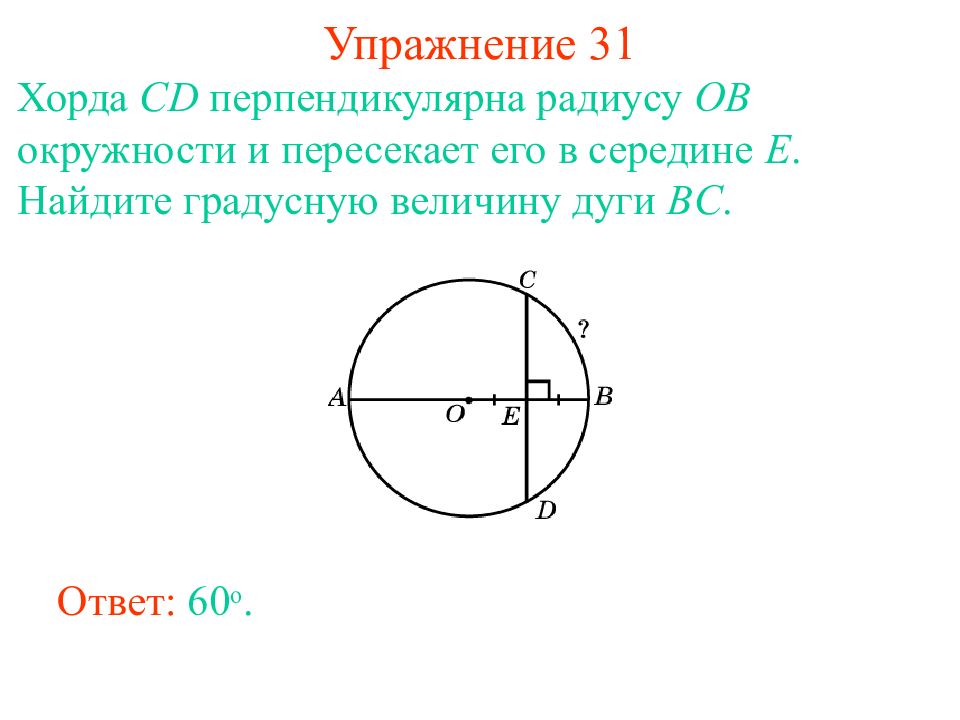
Слайд 38: Упражнение 31
Хорда CD перпендикулярна радиусу OB окружности и пересекает его в середине E. Найдите градусную величину дуги BC. Ответ: 6 0 о.
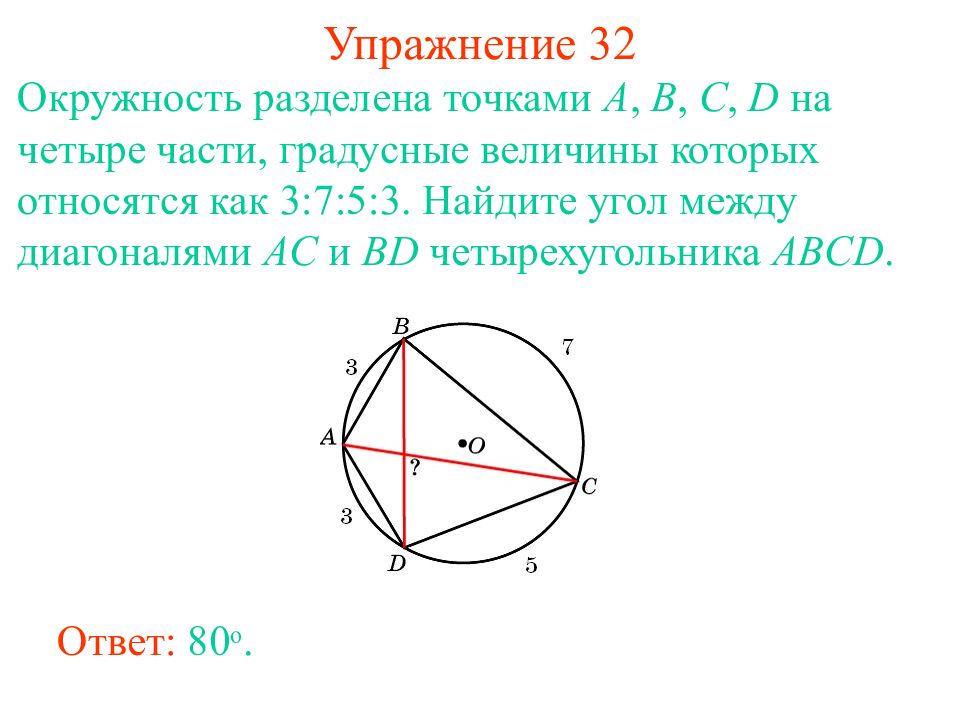
Слайд 39: Упражнение 3 2
Окружность разделена точками A, B, C, D на четыре части, градусные величины которых относятся как 3:7:5:3. Найдите угол между диагоналями AC и BD четырех угольника ABCD. Ответ: 8 0 о.
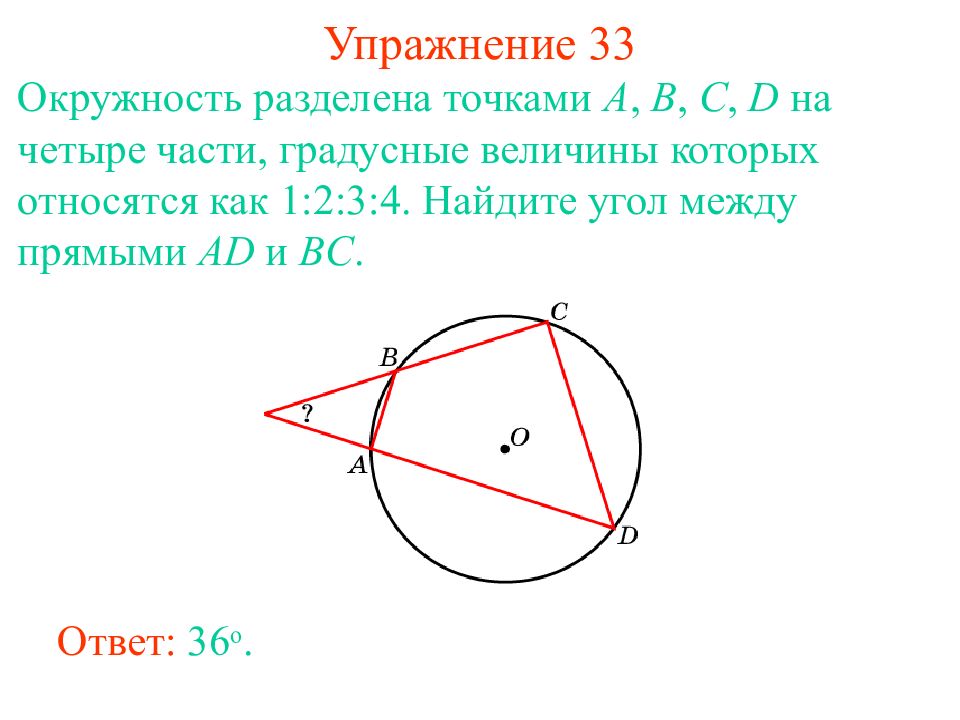
Слайд 40: Упражнение 3 3
Окружность разделена точками A, B, C, D на четыре части, градусные величины которых относятся как 1 : 2 : 3 : 4. Найдите угол между прямыми AD и BC. Ответ: 36 о.
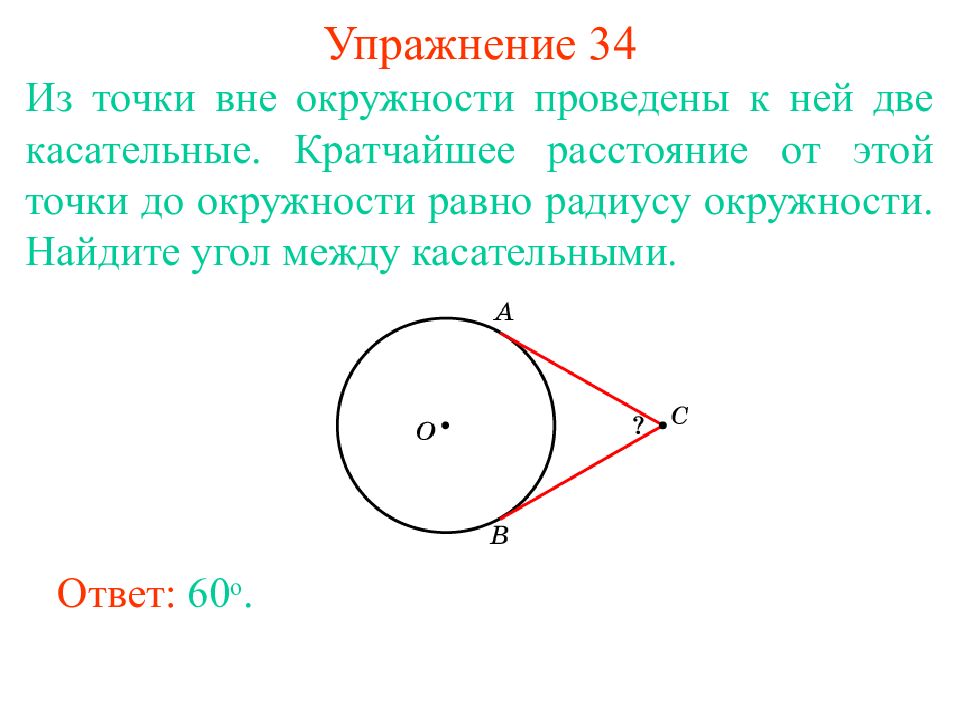
Слайд 41: Упражнение 34
Из точки вне окружности проведены к ней две касательные. Кратчайшее расстояние от этой точки до окружности равно радиусу окружности. Найдите угол между касательными. Ответ: 6 0 о.
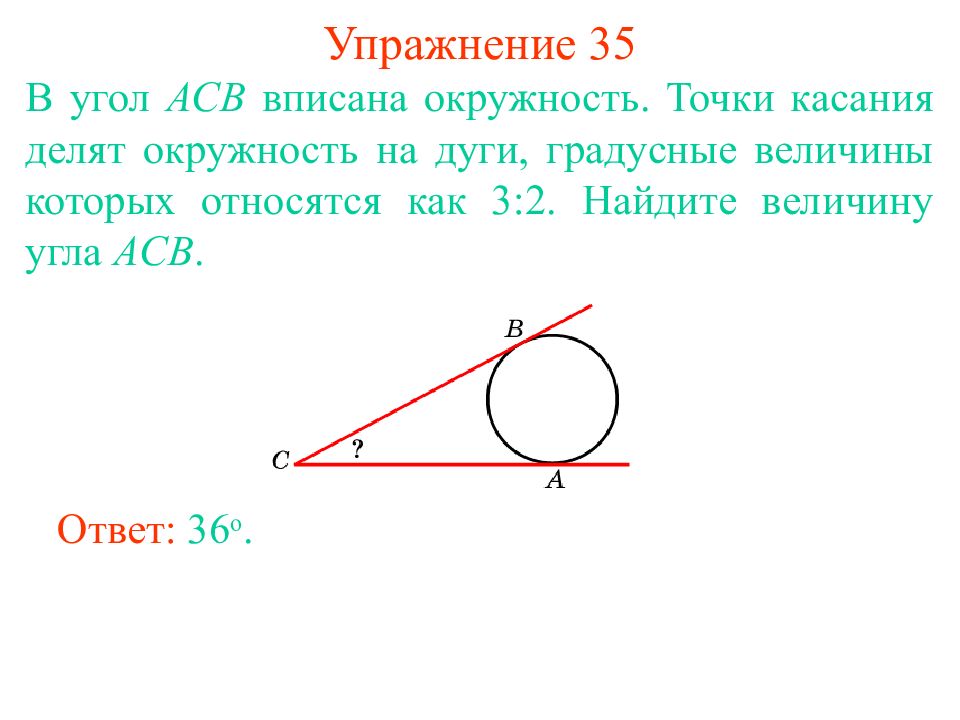
Слайд 42: Упражнение 35
В угол АС B вписана окружность. Точки касания делят окружность на дуги, градусные величины которых относятся как 3 : 2. Найдите величину угла А CB. Ответ: 36 о.
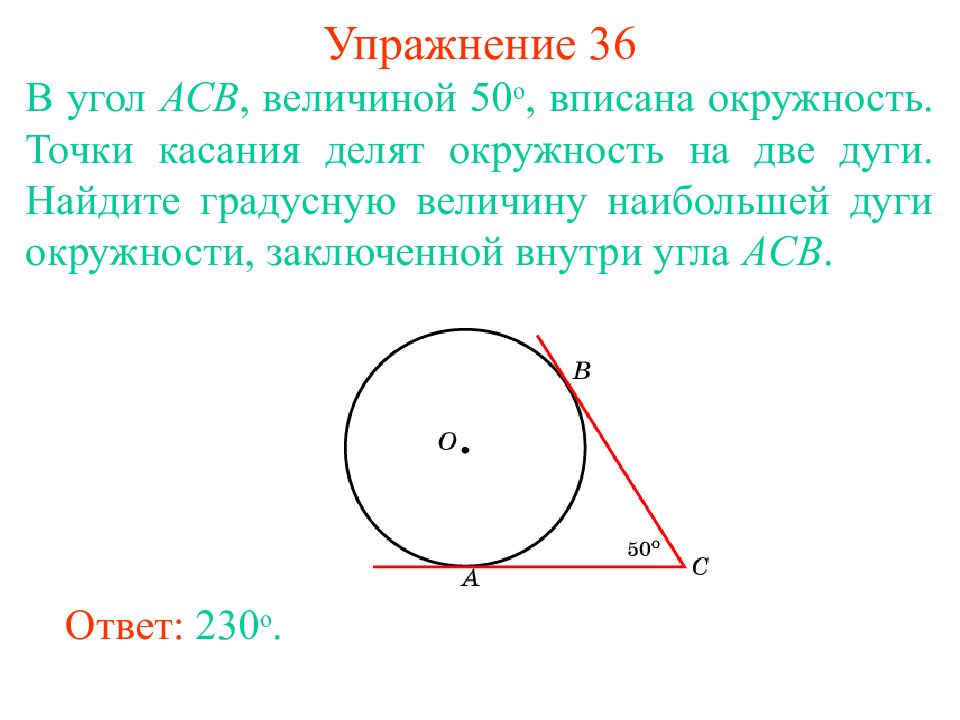
Слайд 43: Упражнение 36
В угол АС B, величиной 5 0 о, вписана окружность. Точки касания делят окружность на две дуги. Найдите градусную величину наибольшей дуги окружности, заключенной внутри угла ACB. Ответ: 230 о.
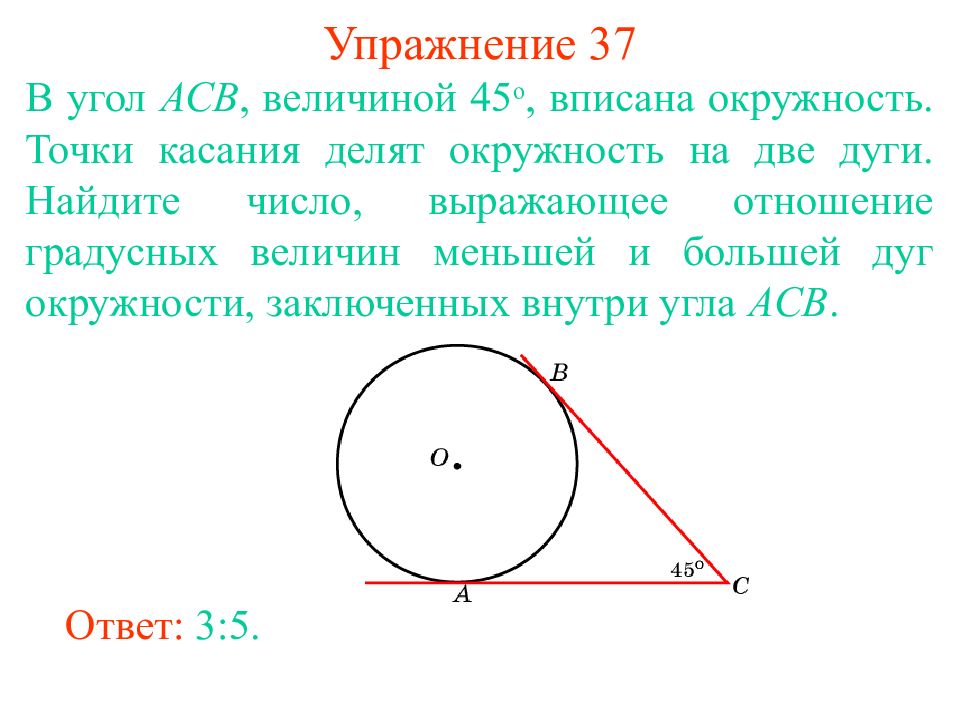
Слайд 44: Упражнение 37
В угол АС B, величиной 45 о, вписана окружность. Точки касания делят окружность на две дуги. Найдите число, выражающее отношение градусных величин меньшей и большей дуг окружности, заключенных внутри угла ACB. Ответ: 3:5.
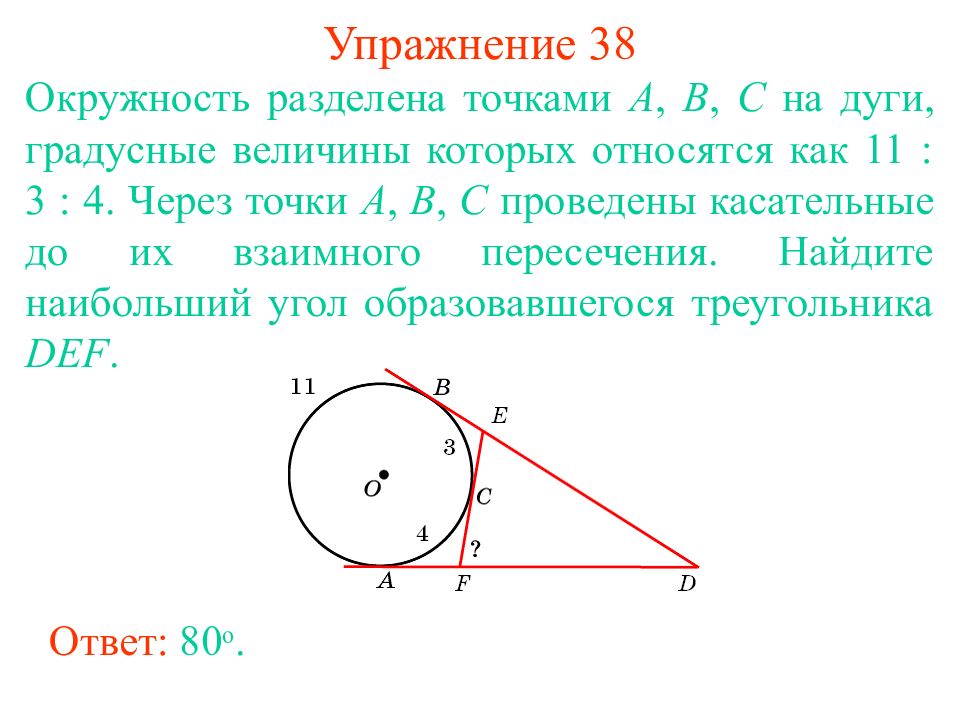
Слайд 45: Упражнение 38
Окружность разделена точками А, В, С на дуги, градусные величины которых относятся как 11 : 3 : 4. Через точки А, В, С проведены касательные до их взаимного пересечения. Найдите наибольший уг ол образовавшегося треугольника DEF. Ответ: 80 о.
Слайд 46: Упражнение 39
Треугольник ABC вписан в окружность. Угол A равен 40 о, угол B равен 60 о. Найдите угол между касательной к окружности, проведенной через вершину C и прямой AB. Ответ: 2 0 о.
Слайд 47: Упражнение 40
Треугольник ABC вписан в окружность. Угол A равен 40 о, угол B равен 60 о. Найдите угол между касательными к окружности, проведенной через вершины A и B. Ответ: 2 0 о.
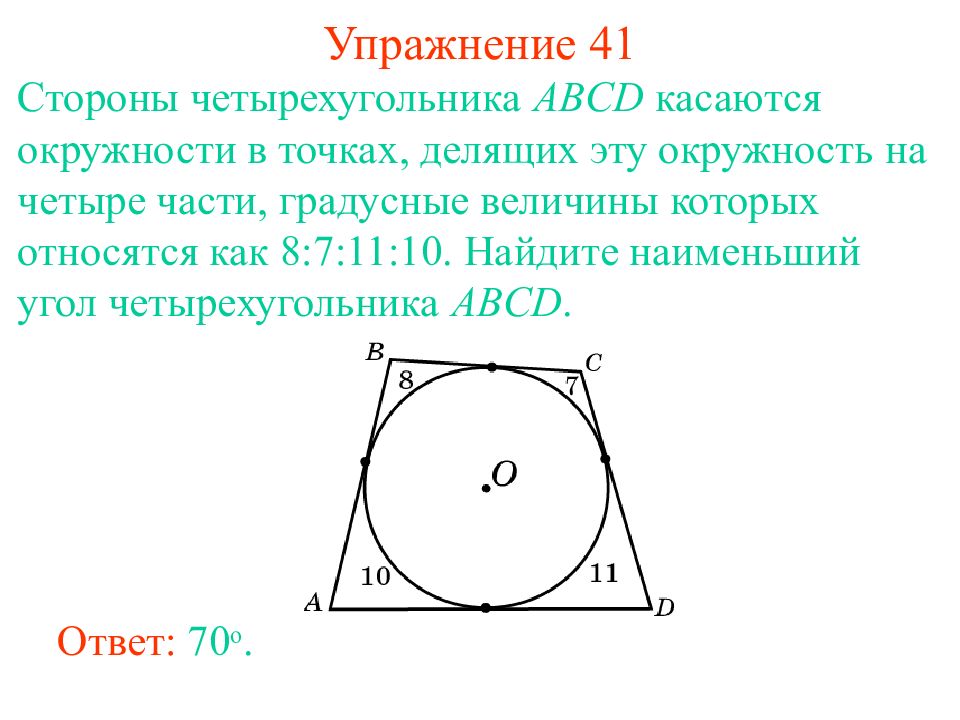
Слайд 48: Упражнение 41
Стороны четырехугольника ABCD касаются окружности в точках, делящих эту окружность на четыре части, градусные величины которых относятся как 8:7 : 11 : 10. Найдите наименьший угол четырехугольника ABCD. Ответ: 7 0 о.