Слайд 2: Содержание
I. Понятие вектора в пространстве II. Коллинеарные векторы III. Компланарные векторы IV. Действия с векторами V. Разложение вектора VI. Базисные задачи Проверь себя Об авторе Помощь в управлении презентацией Выход
Слайд 3: Понятие вектора в пространстве
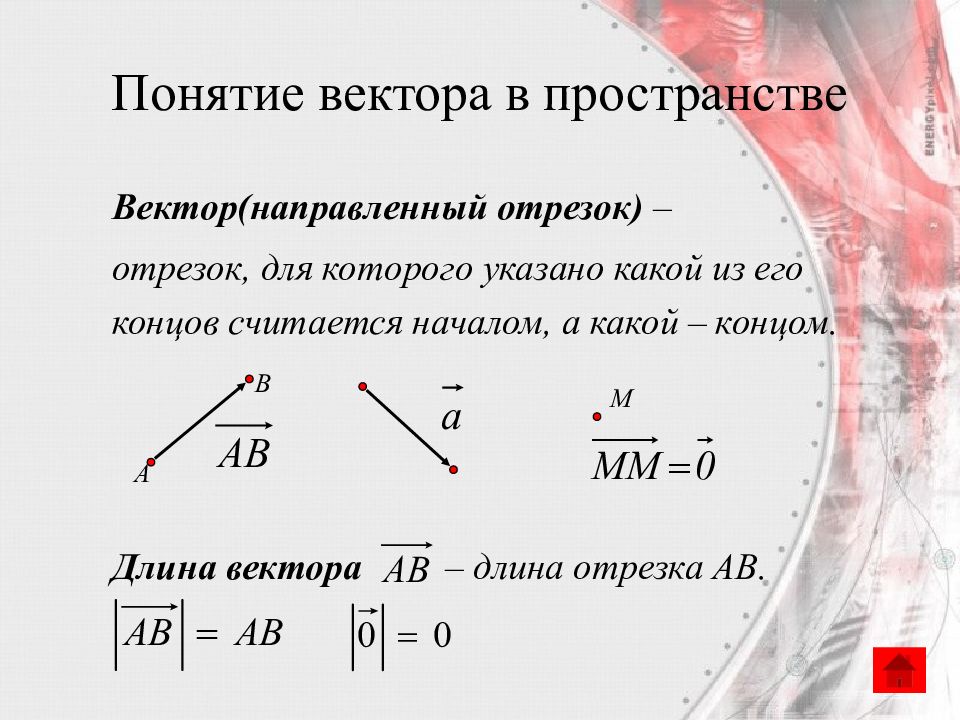
Вектор(направленный отрезок) – отрезок, для которого указано какой из его концов считается началом, а какой – концом. Длина вектора – длина отрезка AB. А В M
Слайд 4: Коллинеарные векторы
Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или параллельных прямых. Среди коллинеарных различают: Сонаправленные векторы Противоположно направленные векторы
Слайд 5: Сонаправленные векторы
Сонаправленные векторы - векторы, лежащие по одну сторону от прямой, проходящей через их начала. Нулевой вектор считается сонаправленным с любым вектором. Равные векторы
Слайд 6: Равные векторы
Равные векторы - сонаправленные векторы, длины которых равны. От любой точки можно отложить вектор, равный данному, и притом только один.
Слайд 7: Противоположно направленные векторы
Противоположно направленные векторы – векторы, лежащие по разные стороны от прямой, проходящей через их начала. Противоположные векторы
Слайд 8: Противоположные векторы
Противоположные векторы – противоположно направленные векторы, длины которых равны. Вектором, противоположным нулевому, считается нулевой вектор.
Слайд 11: Определение компланарных векторов
Компланарные векторы – векторы, при откладывании которых от одной и той же точки пространства, они будут лежать в одной плоскости. Пример: B А C D A 1 B 1 C 1 D 1
Слайд 12: О компланарных векторах
Любые два вектора всегда компланарны. Три вектора, среди которых имеются два коллинеарных, компланарны. α если
Слайд 14: Задачи на компланарность
Компланарны ли векторы: а) б) Справка Решение Известно, что векторы, и компланарны. Компланарны ли векторы: а) б) Справка Решение
Слайд 20: Действия с векторами
Сложение Вычитание Умножение вектора на число Скалярное произведение
Слайд 21: Сложение векторов
Правило треугольника Правило параллелограмма Правило многоугольника Правило параллелепипеда Свойства сложения
Слайд 23: Правило треугольника
А B C Для любых трех точек А, В и С справедливо равенство:
Слайд 26: Правило многоугольника
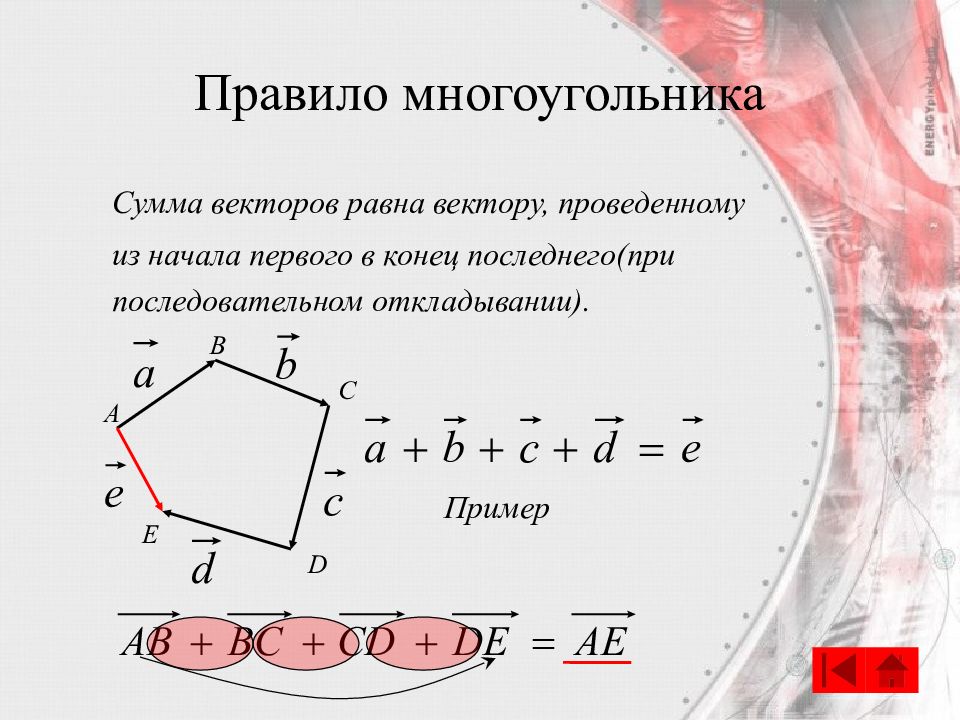
Сумма векторов равна вектору, проведенному из начала первого в конец последнего(при последовательном откладывании). B A C D E Пример
Слайд 28: Правило параллелепипеда
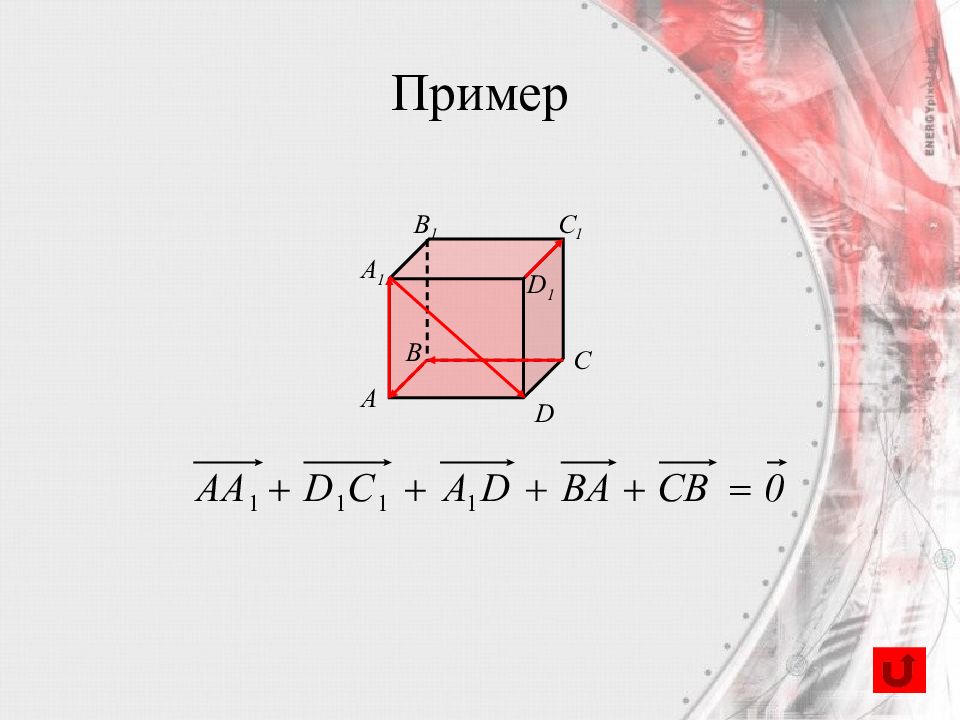
B А C D A 1 B 1 C 1 D 1 Вектор, лежащий на диагонали параллелепипеда, равен сумме векторов, проведенных из той же точки и лежащих на трех измерениях параллелепипеда.
Слайд 31: Вычитание
Разностью векторов и называется такой вектор, сумма которого с вектором равна вектору.
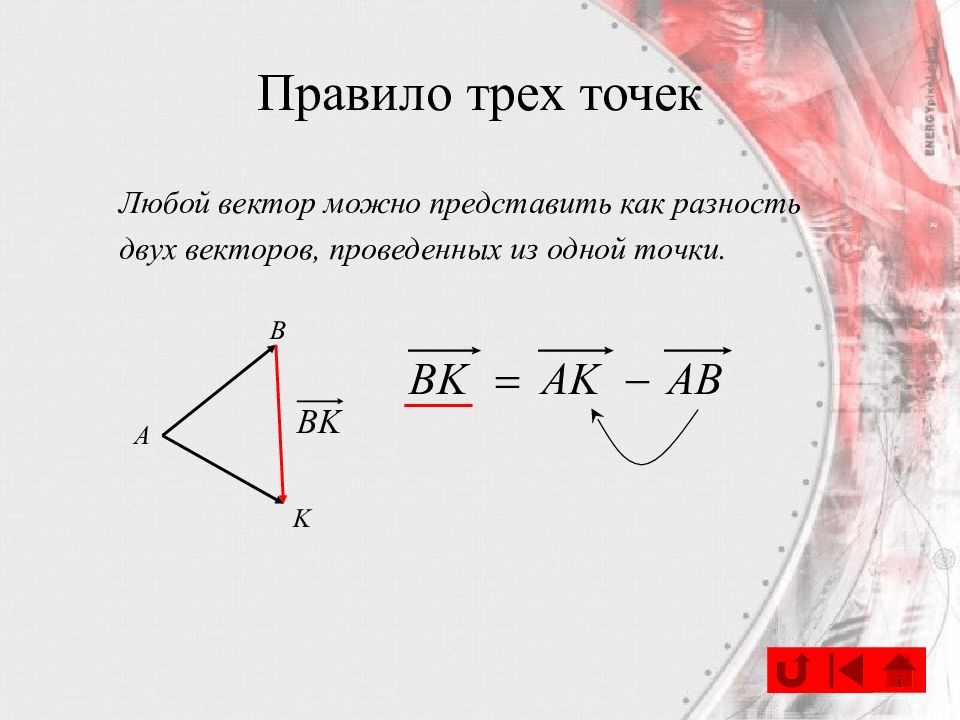
Слайд 33: Правило трех точек
Любой вектор можно представить как разность двух векторов, проведенных из одной точки. А B K
Слайд 34: Сложение с противоположным
Разность векторов и можно представить как сумму вектора и вектора, противоположного вектору. А B O
Слайд 36: Свойства
Произведением нулевого вектора на любое число считается нулевой вектор. Произведение любого вектора на число нуль есть нулевой вектор.
Слайд 38: Скалярное произведение
Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними. Справедливые утверждения Вычисление скалярного произведения в координатах Свойства скалярного произведения
Слайд 39: Справедливые утверждения
скалярное произведение ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны скалярный квадрат вектора (т.е. скалярное произведение вектора на себя) равен квадрату его длины
Слайд 43: Свойства скалярного произведения
1 0. 2 0. 3 0. 4 0. (переместительный закон) (распределительный закон) (сочетательный закон)
Слайд 44: Разложение вектора
По двум неколлинеарным векторам По трем некомпланарным векторам
Слайд 45: Разложение вектора по двум неколлинеарным векторам
Теорема. Любой вектор можно разложить по двум данным неколлинеарным векторам, причем коэффициенты разложения определяются единственным образом. Доказательство
Слайд 46: Доказательство теоремы
O A A 1 B P Пусть коллинеарен. Тогда, где y – некоторое число. Следовательно, т.е. разложен по векторам и.
Слайд 47: Доказательство теоремы
не коллинеарен ни вектору, ни вектору. Отметим О – произвольную точку. Доказательство теоремы
Слайд 48: Доказательство теоремы
Докажем, что коэффициенты разложения определяются единственным образом. Допустим: Тогда: -
Слайд 49: Разложение вектора по трем некомпланарным векторам
Если вектор p представлен в виде где x, y, z – некоторые числа, то говорят, что вектор разложен по векторам, и. Числа x, y, z называются коэффициентами разложения. Теорема Любой вектор можно разложить по трем данным некомпланарным векторам, причем коэффициенты разложения определяются единственным образом. Доказательство
Слайд 51: Доказательство теоремы
Докажем, что коэффициенты разложения определяются единственным образом. Допустим: Тогда: -
Слайд 52: Базисные задачи
Вектор, проведенный в середину отрезка Вектор, проведенный в точку отрезка Вектор, соединяющий середины двух отрезков Вектор, проведенный в центроид треугольника Вектор, проведенный в точку пересечения диагоналей параллелограмма Вектор, лежащий на диагонали параллелепипеда
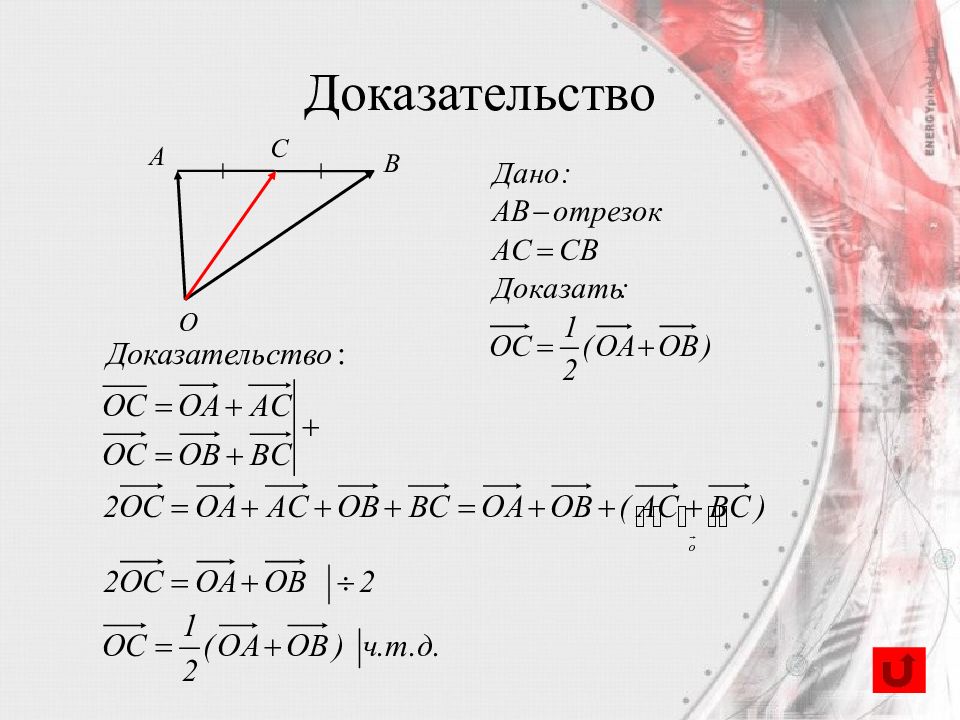
Слайд 53: Вектор, проведенный в середину отрезка,
С A B O Доказательство равен полусумме векторов, проведенных из той же точки в его концы.
Слайд 55: Вектор, проведенный в точку отрезка
С A B O m n Доказательство Точка С делит отрезок АВ в отношении т : п.
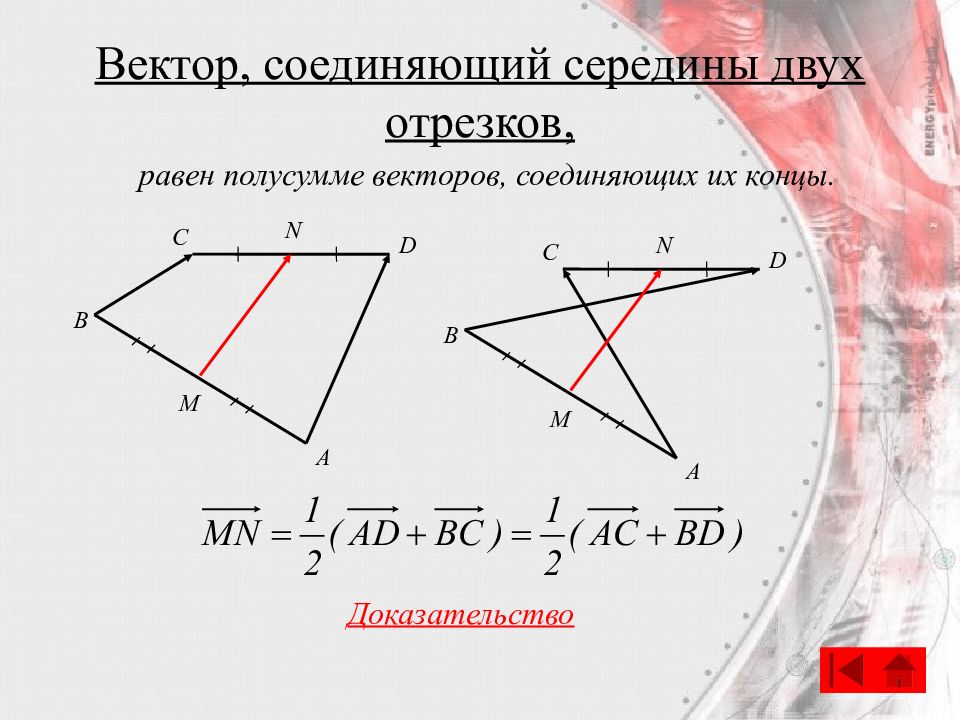
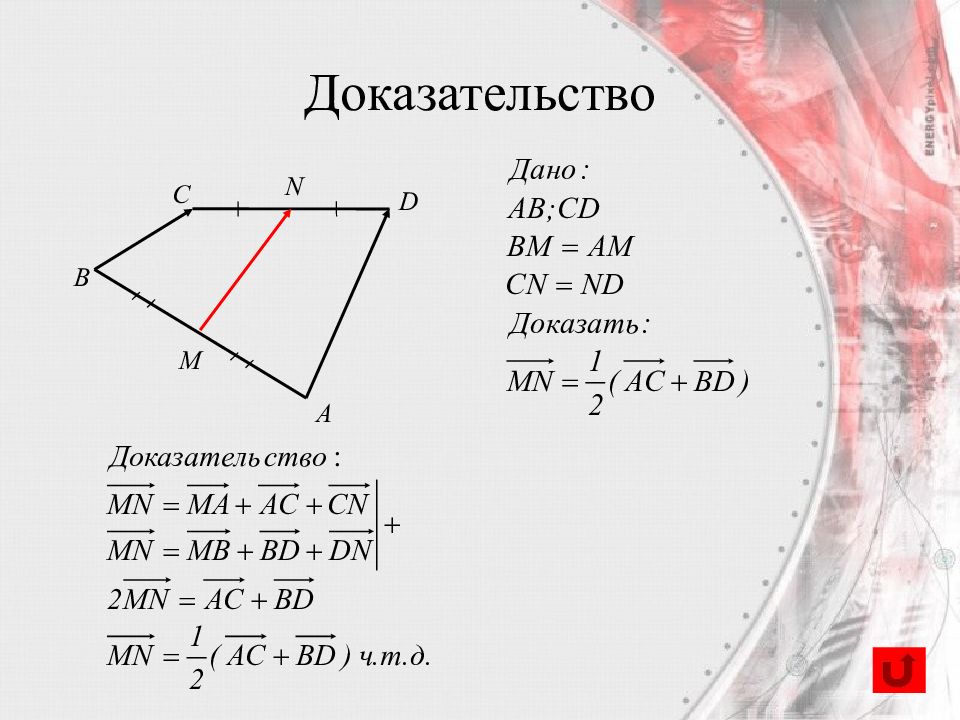
Слайд 57: Вектор, соединяющий середины двух отрезков,
С A B D M N С A B D M N Доказательство равен полусумме векторов, соединяющих их концы.
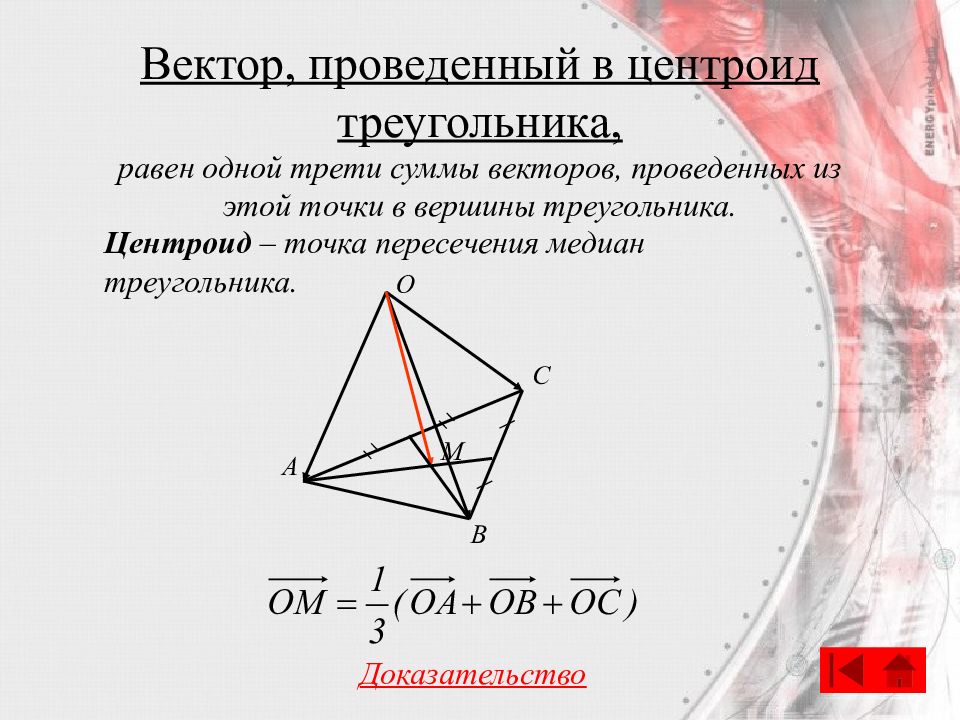
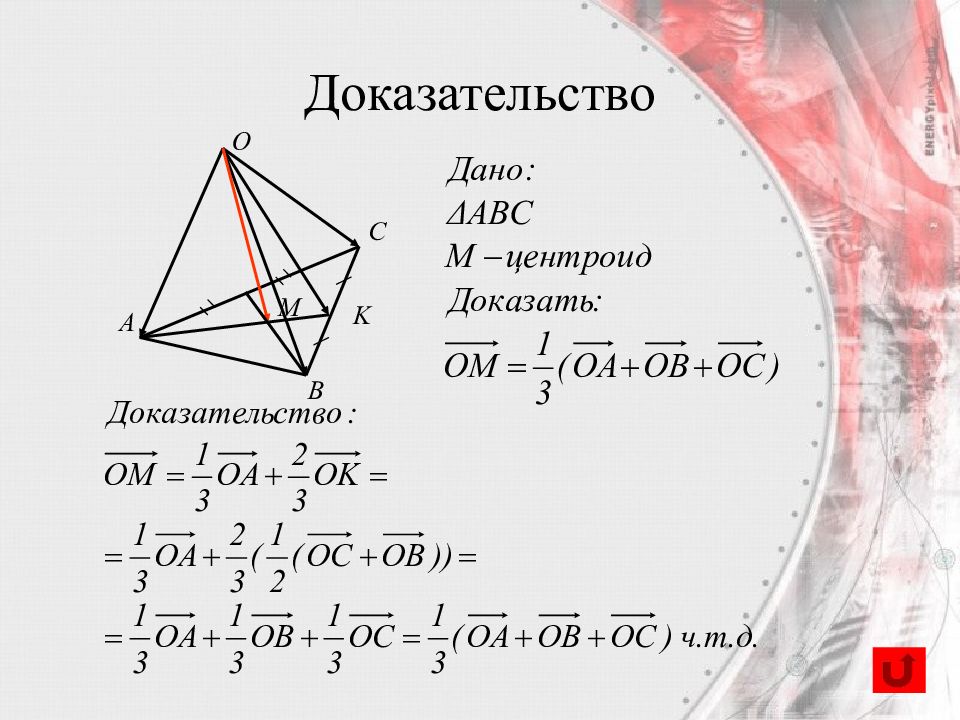
Слайд 59: Вектор, проведенный в центроид треугольника,
Центроид – точка пересечения медиан треугольника. С O A B M Доказательство равен одной трети суммы векторов, проведенных из этой точки в вершины треугольника.
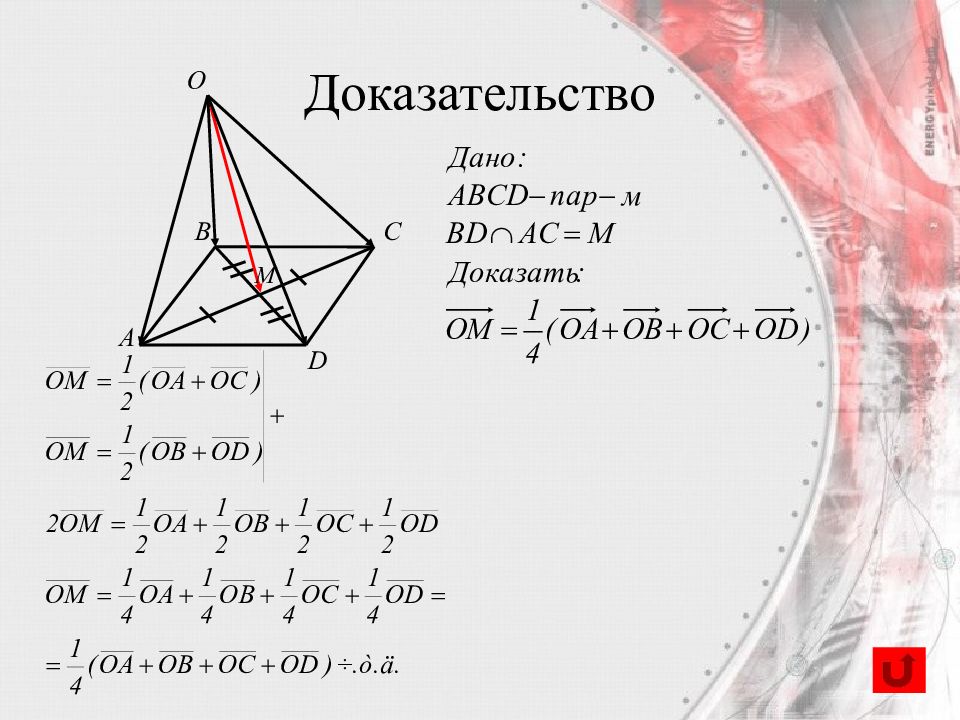
Слайд 61: Вектор, проведенный в точку пересечения диагоналей параллелограмма,
A B C D O M Доказательство равен одной четверти суммы векторов, проведенных из этой точки в вершины параллелограмма.
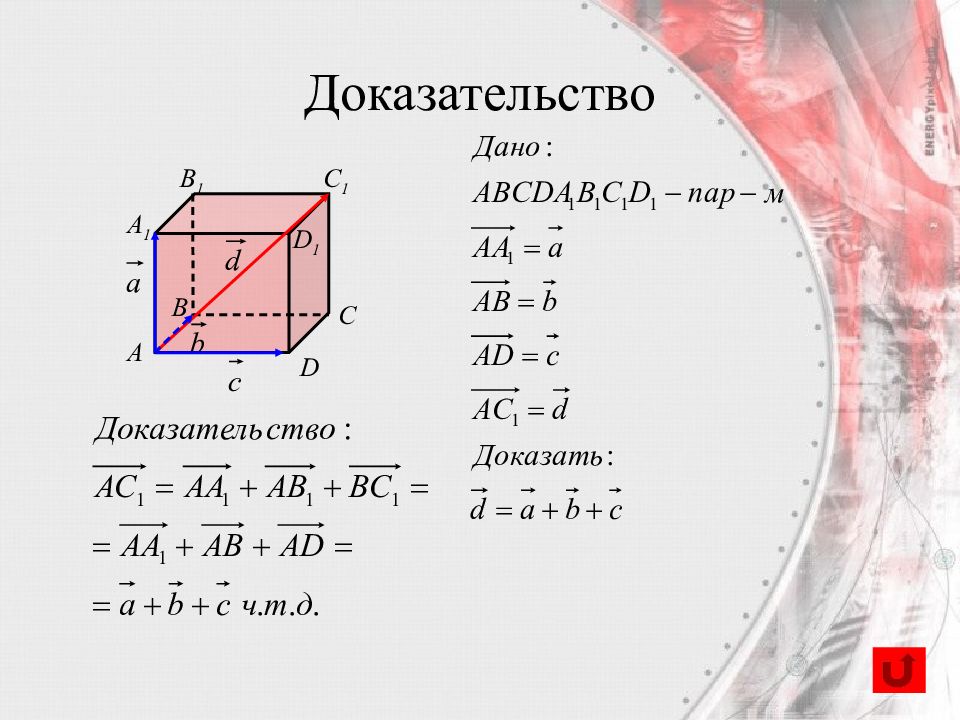
Слайд 63: Вектор, лежащий на диагонали параллелепипеда,
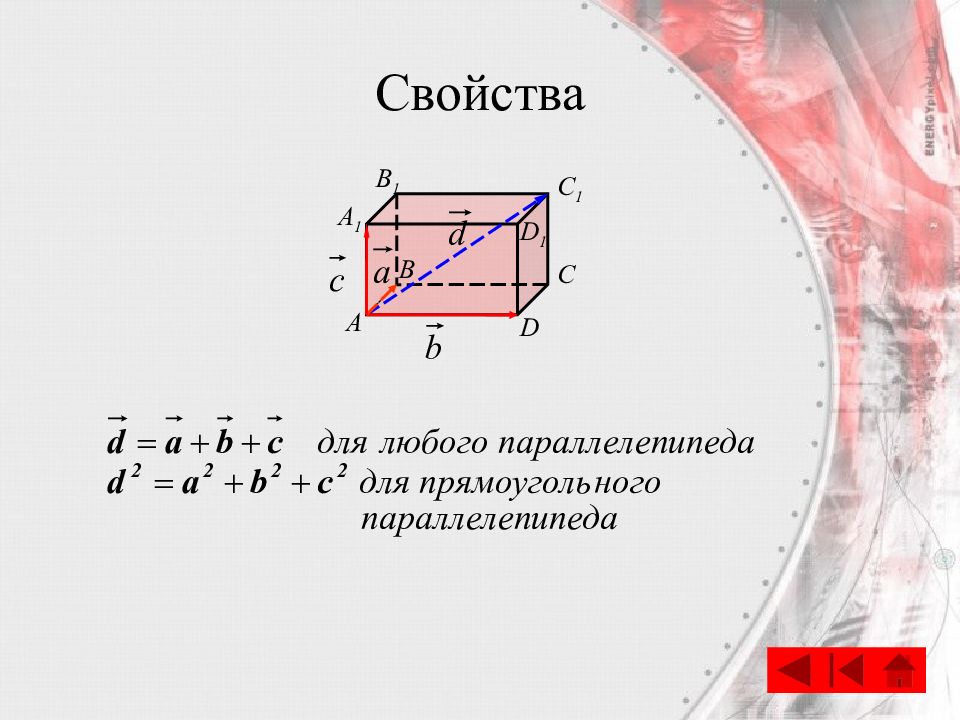
C A B D A 1 B 1 C 1 D 1 Доказательство равен сумме векторов, лежащих на трех его ребрах, исходящих из одной вершины.
Слайд 65: Помощь в управлении презентацией
управление презентацией осуществляется с помощью левой клавиши мыши переход от одного слайда к другому и на гиперссылки по одиночному щелчку завершение презентации при нажатии кнопки выход переход к следующему слайду возврат к содержанию возврат к подтеме возврат с гиперссылок
Слайд 66: Проверь себя
Устные вопросы Задача 1. Задача на доказательство Задача 2. Разложение векторов Задача 3. Сложение и вычитание векторов Задача 4. Скалярное произведение
Слайд 67: Устные вопросы
Справедливо ли утверждение: а) любые два противоположно направленных вектора коллинеарны? б) любые два коллинеарных вектора сонаправлены? в) любые два равных вектора коллинеарны? г) любые два сонаправленных вектора равны? д) е) существуют векторы, и такие, что и не коллинеарны, и не коллинеарны, а и коллинеарны? Ответы
Слайд 68: Ответы
а) ДА б) НЕТ (могут быть и противоположно направленными) в) ДА г) НЕТ (могут иметь разную длину) д) ДА е) ДА
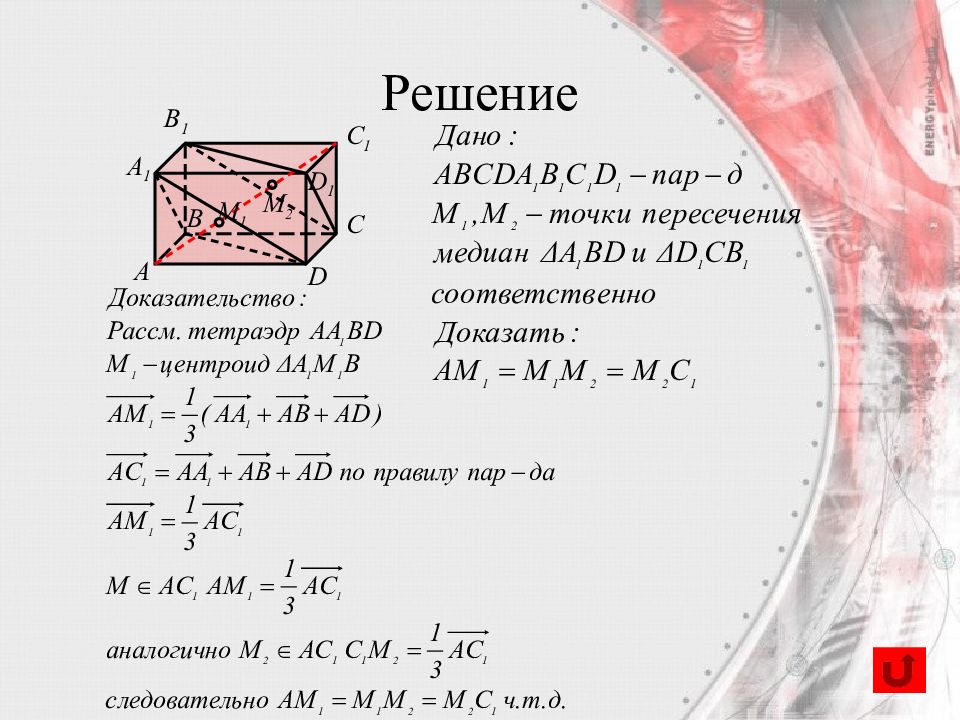
Слайд 69: Задача 1. Задача на доказательство
B А C D A 1 B 1 C 1 D 1 M 1 M 2 Решение
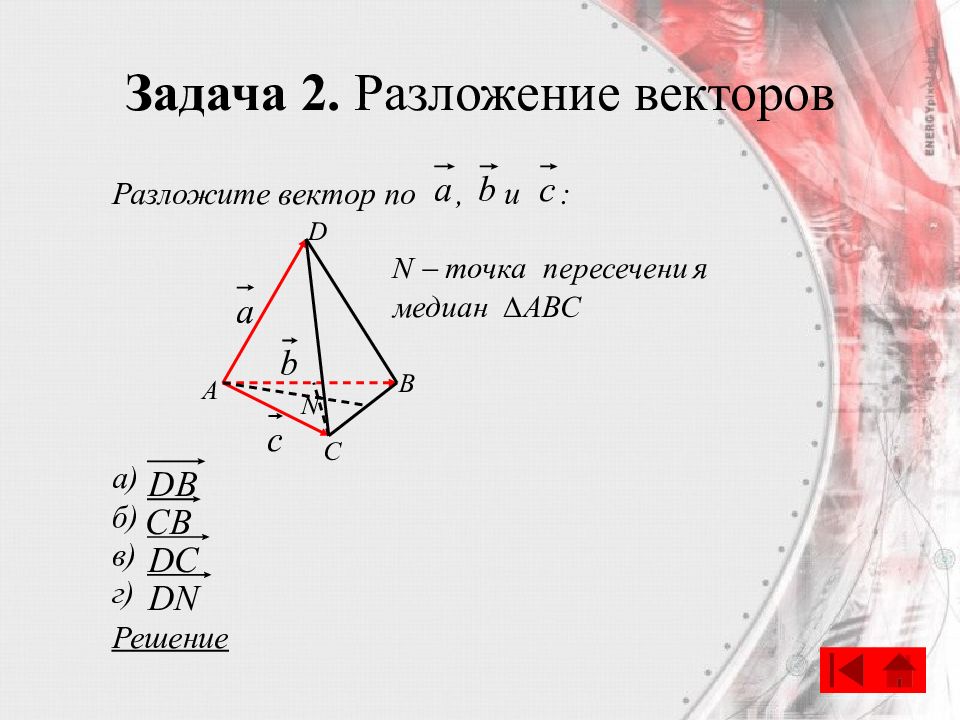
Слайд 71: Задача 2. Разложение векторов
Разложите вектор по, и : а) б) в) г) Решение A B C D N
Слайд 73: Задача 3. Сложение и вычитание
Упростите выражения: а) б) в) г) д) е) Решение
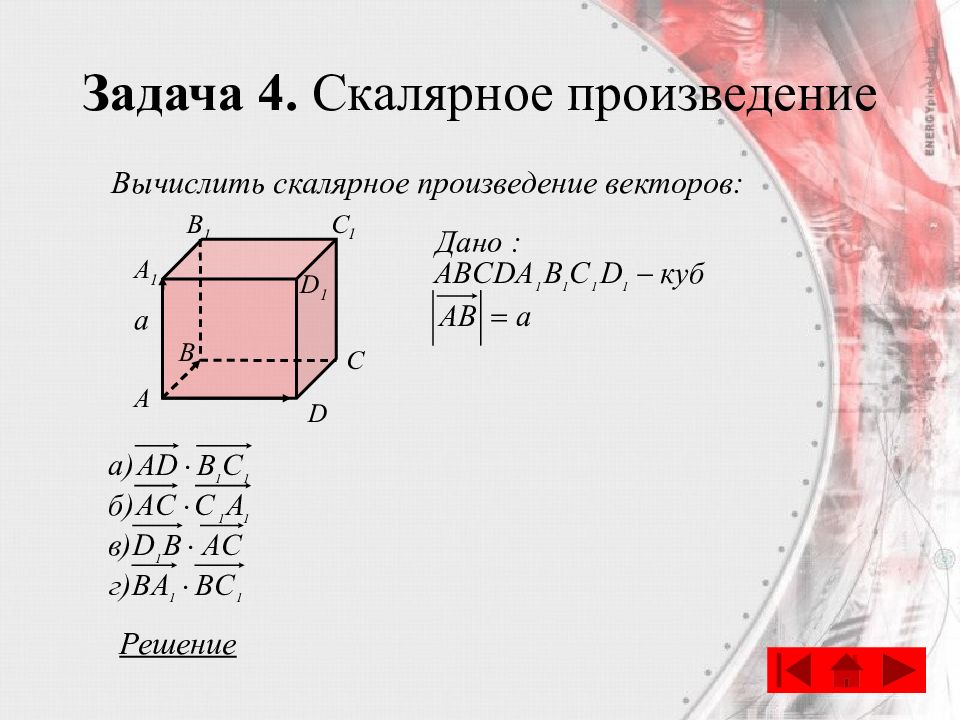
Слайд 75: Задача 4. Скалярное произведение
Вычислить скалярное произведение векторов: C A B D A 1 B 1 C 1 D 1 Решение
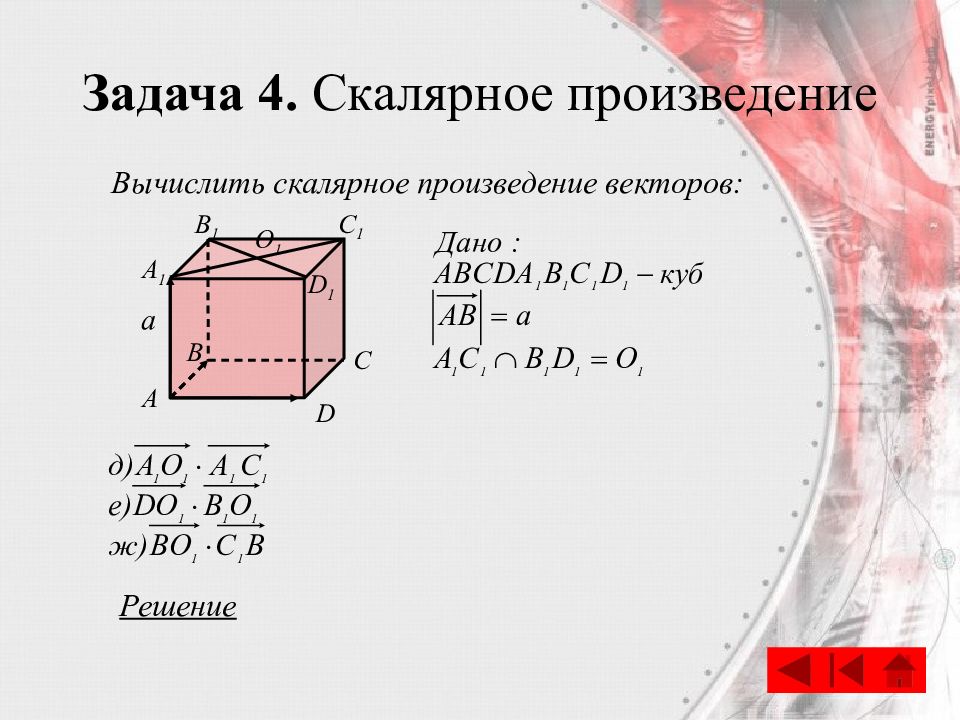
Слайд 76: Задача 4. Скалярное произведение
C A B D A 1 B 1 C 1 D 1 O 1 Вычислить скалярное произведение векторов: Решение