Скалярное произведение в координатах Л.С. Атанасян "Геометрия 7-9" Савченко Е.М., учитель математики, МОУ гимназия №, г. Полярные Зори, Мурманской обл.
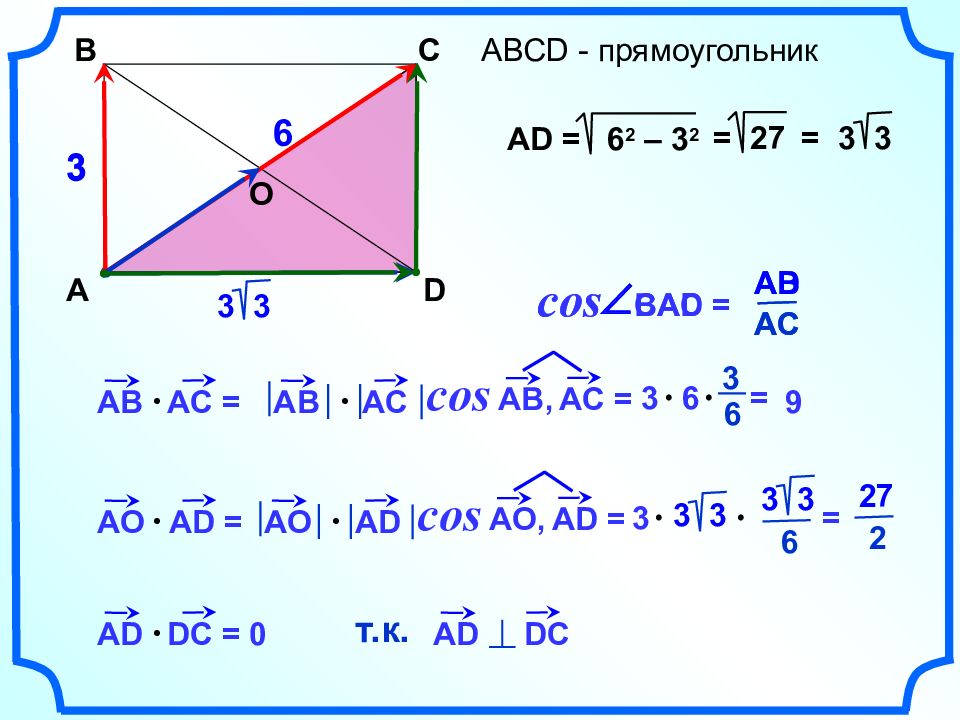
АВС D - прямоугольник A B C D 3 6 A В А C = A О А D = AD DC = AB AC AB, AC = cos 9 O 3 6 = 6 3 = 27 3 3 3 A О AD AO, AD = cos 3 = 3 3 6 3 3 2 27 0 AD DC ^ т.к. AD = 6 2 – 3 2 = 3 3 BAC = cos AC AB Ð CAD = cos AC AD Ð
Скалярное произведение векторов и выражается формулой a { x 1 ; y 1 } b { x 2 ; y 2 } Теорема = x 1 x 2 + y 1 y 2 a b Случай, когда один из векторов нулевой a { x 1 ; y 1 } 0 { 0 ; 0 } = x 1 0 + y 1 0 a 0 Доказательство:
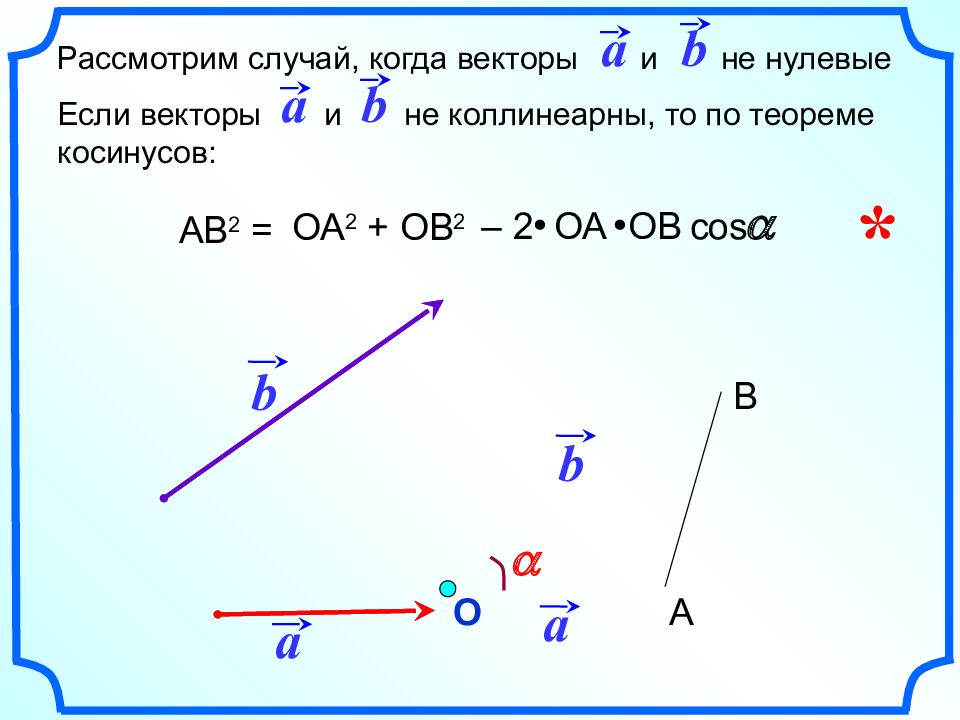
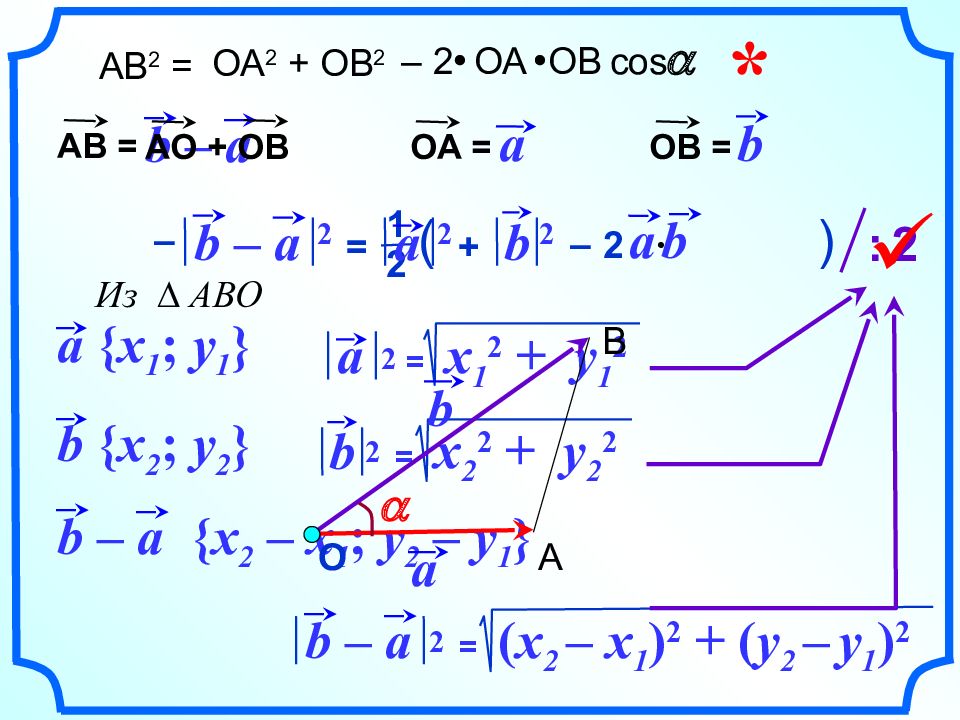
a b a b a О А В Рассмотрим случай, когда векторы и не нулевые a b AB 2 = ОА 2 + ОВ 2 – 2 ОА ОВ cos a Если векторы и не коллинеарны, то по теореме косинусов: a b *
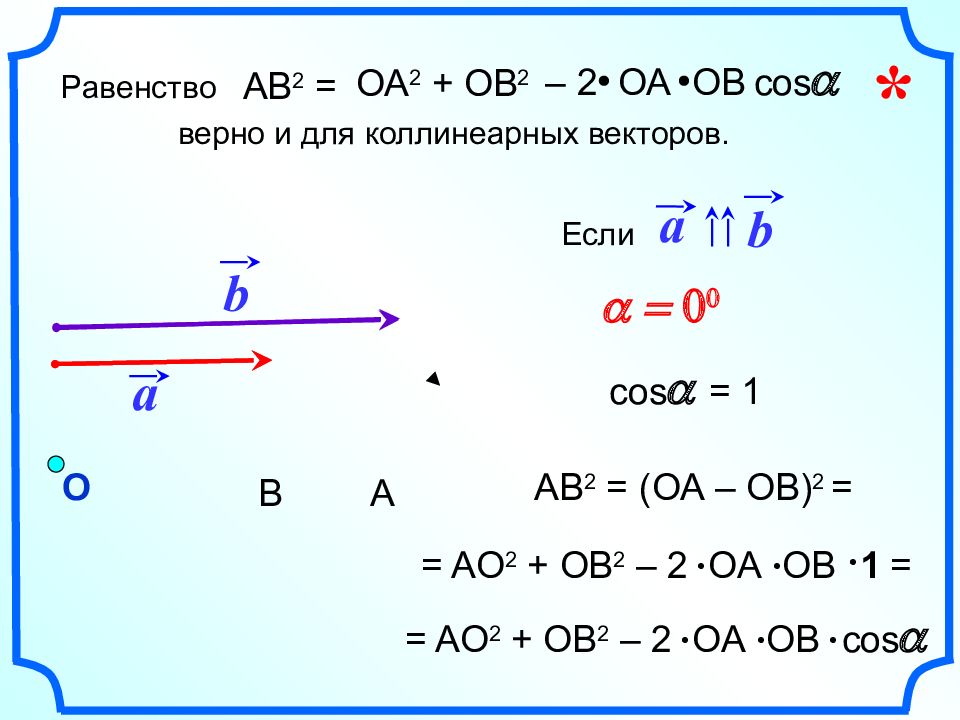
a b a = 0 0 О А В AB 2 = (ОА – ОВ) 2 = с os = 1 a = A О 2 + ОВ 2 – 2 ОА ОВ cos a = A О 2 + ОВ 2 – 2 ОА ОВ Если a b = 1 Равенство верно и для коллинеарных векторов. AB 2 = ОА 2 + ОВ 2 – 2 ОА ОВ cos a *
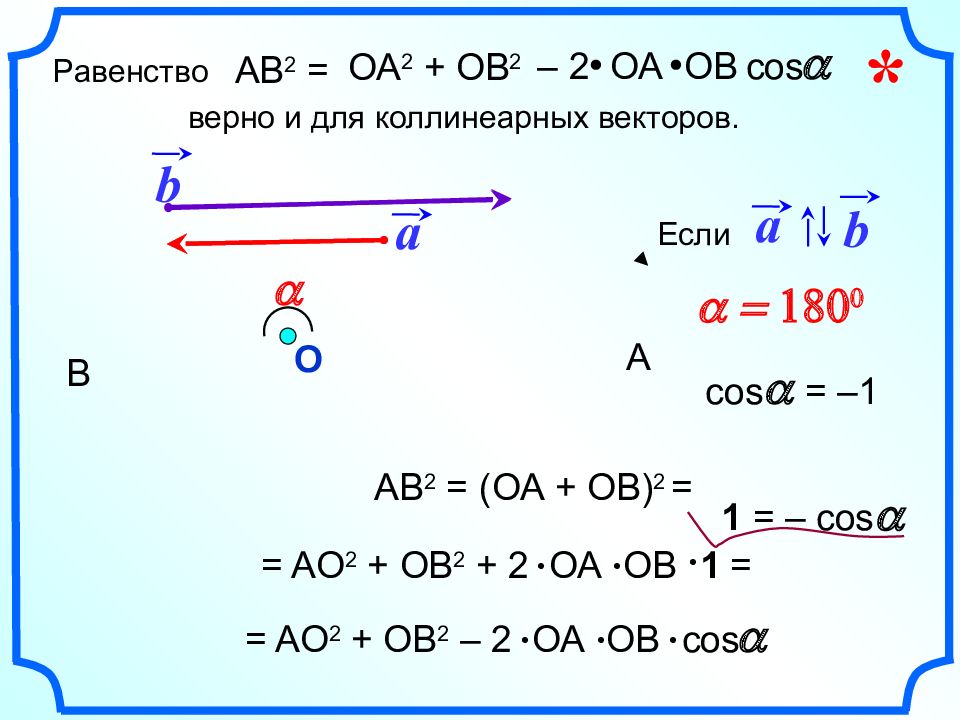
a b a = 180 0 О А В AB 2 = (ОА + ОВ) 2 = с os = –1 a = A О 2 + ОВ 2 + 2 ОА ОВ cos a = A О 2 + ОВ 2 – 2 ОА ОВ Если a b = 1 a 1 = – с os a Равенство верно и для коллинеарных векторов. AB 2 = ОА 2 + ОВ 2 – 2 ОА ОВ cos a *
b = x 2 2 + y 2 2 2 1 ( ) = AB 2 = ОА 2 + ОВ 2 – 2 ОА ОВ cos a * b – a AB = b OA = a OB = b – a 2 a 2 b 2 + – – a b a { x 1 ; y 1 } b { x 2 ; y 2 } b – a { x 2 – x 1 ; y 2 – y 1 } a = x 1 2 + y 1 2 2 2 b – a = ( x 2 – x 1 ) 2 + ( y 2 – y 1 ) 2 2 2 : 2 a b a О А В AO + OB
d { 2 ; 4} 2 Ненулевые векторы и перпендикулярны тогда и только тогда, когда x 1 x 2 + y 1 y 2 = 0 a b Следствие 1 a b ^ Û x 1 x 2 + y 1 y 2 = 0 b { -2 ; 1 } b d ^ Пример + -2 1 4 = 0
Косинус угла между ненулевыми векторами и выражается формулой a b Следствие 2 cos = a x 1 x 2 + y 1 y 2 x 1 2 + y 1 2 x 2 2 + y 2 2
Следствие 2 Доказательство: a = b = x 2 2 + y 2 2 a b a b = a b cos a cos a = a b = x 1 x 2 + y 1 y 2 a b = x 1 x 2 + y 1 y 2 x 1 2 + y 1 2 x 1 2 + y 1 2 x 2 2 + y 2 2
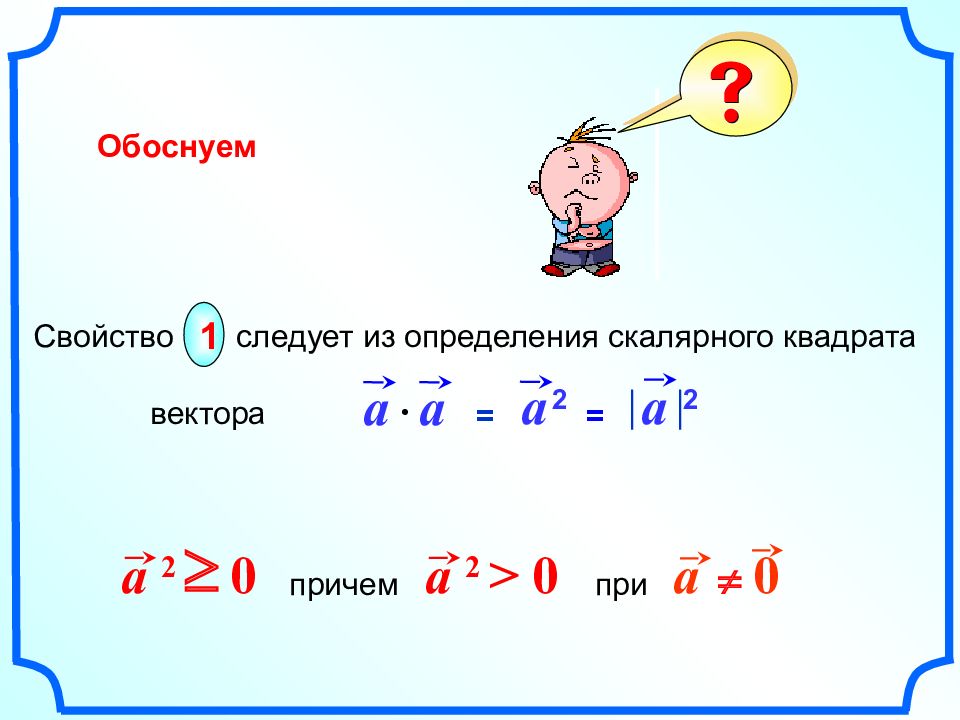
Сочетательный закон Переместительный закон Распределительный закон 1 2 3 Свойства скалярного произведения векторов Для любых векторов,, и любого числа справедливы равенства: a b b k c 4 a 2 0 ³ причем при a 2 > 0 a 0 ¹ a b b a = ( a + b ) c = a c + b c ( k a ) b k ( a b ) =
1 Свойство следует из определения скалярного квадрата вектора a 2 0 ³ причем при a 2 > 0 a 0 ¹ a a a 2 a 2 = = Обоснуем
Свойство следует из определения скалярного произведения векторов 2 = x 1 x 2 + y 1 y 2 a b = a b x 2 + x 1 y 1 y 2 a b b a = Переместительный закон a b b a =
= x 1 x 3 + + + y 2 y 3 = ( ) ( ) 3 Докажем свойство Рассмотрим векторы a { x 1 ; y 1 } b { x 2 ; y 2 } c { x 3 ; y 3 } ( a + b ) c = ( x 1 + x 2 ) x 3 + ( y 1 + y 2 ) y 3 = = a c + b c Распределительный закон ( a + b ) c = a c + b c x 2 x 3 y 1 y 3
4 Докажем свойство Рассмотрим векторы a { x 1 ; y 1 } ka { kx 1 ; ky 1 } ( k a ) b = ( k x 1 ) x 2 + ( k y 1 ) y 2 = = k ( x 1 x 2 + y 1 y 2 ) = = k ( a b ) b { x 2 ; y 2 } Сочетательный закон ( k a ) b k ( a b ) =
Распределительный закон имеет место для любого числа слагаемых. Например, ( a + b + c ) d = a d + b d + c d ( a + b ) c = a c + b c
a { 3 ; -4 } b { -2 ; 1 } Найдите c {-2; - 1,5} a b b c c a = 3 (-2) + (-4) 1 = - 10 = (-2) (-2) + 1 (- 1,5) = 2,5 = 3 (-2) + (-4) (- 1,5) = 0 Перпендикулярны ли векторы и, и, и a b b c c a Каким (острым, тупым или прямым) является угол между векторами и, и, и a b b c c a тупой острый прямой
b d ^ b d ^ Û x 1 x 2 + y 1 y 2 = 0 x = 2 * d { ? ; 4} x b { -2 ; 1 } + -2 1 4 = 0 Найдите абсциссу вектора, если известно, что d
a { 4 ; -2} i Найдите c {-2; - 1,5} a i c j i j = 4 1 + (-2) 0 = 4 = (-2) 0 + (- 1,5) 1 = - 1,5 = 1 0 + 0 1 = 0 Перпендикулярны ли векторы и, и, и a i c j i j Каким (острым, тупым или прямым) является угол между векторами и, и, и a i c j i j острый тупой прямой { 1; 0} j { 0; 1}
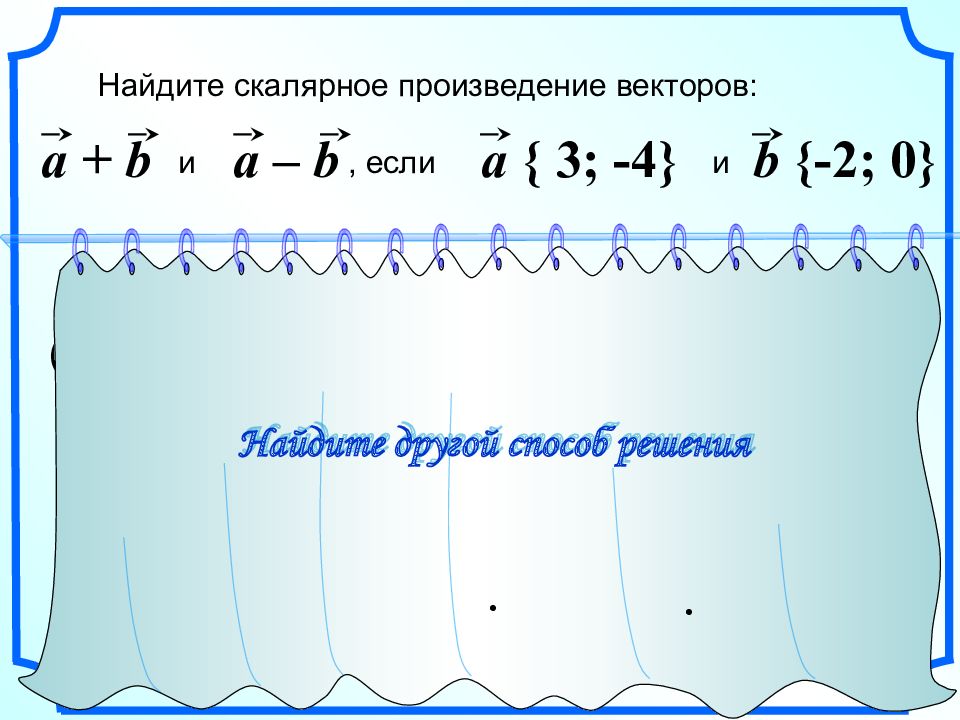
b { -2 ; 0 } Найдите скалярное произведение векторов: и, если и a + b a – b a { 3; -4} = a 2 – b 2 ( a + b )( a – b ) a = 3 2 + (-4) 2 = 25 = a 2 – b 2 a 2 = 25 b = (-2) 2 + 0 2 = 4 b 2 = 4 = 25 – 4 = 21 Восстановите решение
b { -2 ; 0 } Найдите скалярное произведение векторов: и, если и a + b { 1; -4 } a – b a { 3; -4} ( a + b )( a – b ) 1 2 3 1 2 3 a + b a – b { 5; -4 } ( a + b )( a – b ) = 1 5 + (-4) (-4) = 21 Найдите другой способ решения
Найдите скалярное произведение векторов: и, если и – координатные векторы. i – j 2 i + 3 j i j = j ( i – j )(2 i + 3 j ) = 2 i 2 + 3 i j – 2 i j – 3 j 2 = i = 0 0 1 1 = 2 i 2 – 3 j 2 = 2 1 – 3 1 = – 1 Восстановите решение
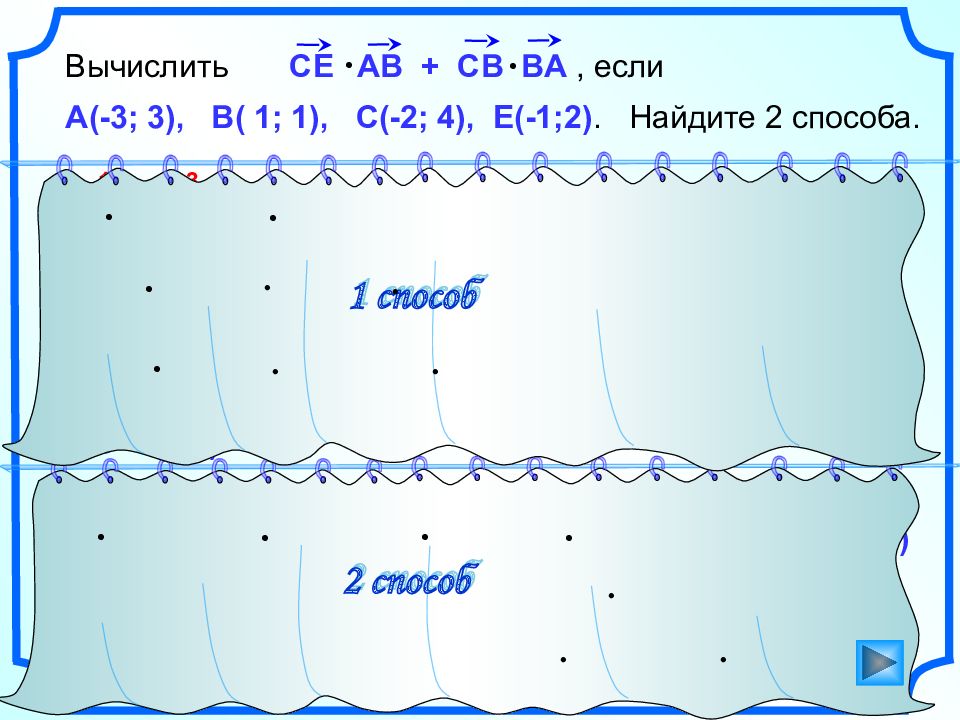
Вычислить, если А(-3 ; 3), В( 1; 1), С(-2; 4), Е(-1;2). Найдите 2 способа. CE AB + CB BA CE AB + CB BA 1 2 3 CE AB = 1 4 + (-2) (-2) = 8 BA { - 4; 2} CB BA = 3 (-4) + (-3) 2 = -18 1 2 3 8 + (-18) = -10 = CE AB + CB (– AB ) = AB ( CE – CB ) = AB ( CE + BC ) = AB (В C + C Е) = AB ВЕ = CE AB + CB BA = 4 (-2) + (-2) 1 = -10 CE { 1; -2} AB { 4; -2} C В { 3 ; - 3 } B Е { - 2 ; 1 } 2 способ 1 способ
Вычислить если,, a = 5 b = 8 a + b a b = 60 0 C калярный квадрат вектора равен квадрату его длины. a 2 = a 2 a + b 2 ( a + b ) 2 = = a 2 + 2 a b + b 2 = a 2 + 2 a b cos a b + b 2 = 5 2 + 2 5 8 cos 60 0 + 8 2 = 5 2 + 2 5 8 + 8 2 1 2 = 129 a + b = 129 №1050 = = = ( a + b ) 2 a + b 2 = 129
= 4 9 ( a – b ) 2 a – b 2 a – b Вычислить если,, a = 5 b = 8 a – b a b = 60 0 C калярный квадрат вектора равен квадрату его длины. a 2 = a 2 a – b 2 ( a – b ) 2 = = a 2 – 2 a b + b 2 = a 2 – 2 a b cos a b + b 2 = 5 2 – 2 5 8 cos 60 0 + 8 2 = 5 2 – 2 5 8 + 8 2 1 2 = 4 9 = 4 9 №1050 = = = Восстановите решение
