Первый слайд презентации: величины
Слайд 2
Аддитивно-скалярная величина – это свойство, позволяющее отобразить множество объектов на множество Свойства: а b a = b + c + f(c) f(c) = 1 g(a) = k f (a) f М ед.
Слайд 3: Однородные величины
Величины, которые выражают одно и тоже свойство объектов некоторого множества, называются величинами одного рода или однородными величинами. длина площадь разнородные величины
Слайд 4: Свойства однородных величин
Любые две величины одного рода сравнимы : они либо равны, либо одна меньше другой. a, b ): a b, a = b, ab 2. Величины одного рода можно складывать, в результате сложения получится величина того же рода. a, b ): a + b – сумма величин a и b. А В С а b a + b
Слайд 5
3. Величину умножают на действительное число, получая в результате величину того же рода. a ) x R + : b = x a b - произведение величины а на число х А В С а а 2а 4. Величины одного рода вычитают, определяя разность величин через сумму: разностью величин а и b называется такая величина с, что а = b + с. А В С b с a c = а - b
Слайд 6
5. Величины одного рода делят, определяя частное через произведение величины на число: частным величин а и b называется такое неотрицательное действительное число х, что а = х b. = x, х – отношение величин а и b. = 2 А В С а а 2а
Преобразование единиц Арифметические действия Решение задач
Слайд 8
Измерение – процесс определения отношения измеряемой величины к другой однородной величине, которая принята за единицу (эталон). В результате измерения получается отвлеченное число, которое показывает, сколько раз единица величины е содержится в измеряемой величине ; или какую часть этой единицы составляет измеряемая величина. Это число называется мерой или числовым значением величины. Измерение величин
Слайд 9
Числовое значение величины, записанное с указанием единицы величины, называют значением величины или именованным числом. Например: 7 кг = 7 1 кг; 12 см = 12 1 см; 3 ч = 3 1ч именованное число числовое значение величины
Слайд 10: Задания
Выразите: В минутах ч; 8 мин 12 с; В сантиметрах 8 см 79 мм; В тоннах 125 кг 300 г. Сравните величины: 56 мин и ч; 1,5 см и дм ; м и дм. 3 балла
Слайд 11
косвенное измерение измерение, при котором искомое значение величины находится на основании известной зависимости между этой величиной и величинами, подвергаемыми прямым измерениям. Например, сопротивление резистора находим на основании закона Ома подстановкой значений силы тока и напряжения, получаемых в результате прямых измерений. измерение величин прямое измерение измерение, при котором искомое значение физической величины находится непосредственно из опытных данных в результате сравнения измеряемой величины с эталонами. Например, измерение длины линейкой.
Слайд 12: Длина отрезка и ее измерение
Длиной отрезка называется положительная величина, определенная для каждого отрезка так, что: равные отрезки имеют равные длины; если отрезок состоит из конечного числа отрезков, то его длина равна сумме длин этих отрезков. е единица длины
Слайд 13: Основные свойства длин отрезков
При выбранной единице длины длина любого отрезка выражается положительным действительным числом, и для каждого положительного действительного числа есть отрезок, длина которого выражается этим числом. если два отрезка равны, то численные значения их длин также равны, и обратно: если численные значения длин двух отрезков равны, то равны и сами отрезки. a = b m e (a) = m e (b )
Слайд 14
Если данный отрезок есть сумма нескольких отрезков, то численное значение его длины равно сумме численных значений длин отрезков слагаемых, и обратно, если численное значение длины отрезка равно сумме численных значений нескольких отрезков, то и сам отрезок равен сумме этих отрезков. c = a + b m e (c) = m e (a)+m e (b )
Слайд 15
4. Если длины отрезков a и b таковы, что b = xa, где х R + и длина a измерена при помощи единицы е, то, чтобы найти численное значение длины b при единице е, достаточно число х умножить на численное значение длины а при единице е. b = xa m e (b) = x·m e (a ) 5. При замене единицы длины численное значение длины увеличивается (уменьшается) во столько раз, во сколько новая единица меньше (больше) старой.
Слайд 16
a > b m e (a) > m e (b) c = a – b m e (c) = m e (a ) - m e (b) x = a : b m e (a) : m e (b) Например: 12,3 м > 12м, т.к. 12,3 > 12 7,8 см + 3,2 см = (7,8+3,2) см = 11 см 17·3 дм = (17·3) дм = 51 дм В начальном курсе математики длины отрезков и змеряют, строят отрезки заданной длины, сравнивают длины отрезков, производят над ними действия.
Слайд 17: Площадь фигуры и ее измерение
Площадью фигуры называется неотрицательная величина, определенная для каждого отрезка так, что: равные фигуры имеют равные площади; если фигура составлена из конечного числа фигур, то ее площадь равна сумме их площадей. е 2 е е единица площади – площадь квадрата со стороной, равной единичному отрезку е.
Слайд 18: Правила сравнения площадей и действий над ними
Если фигуры равны, то равны численные значения их площадей (при одной и той же единице площади). Фигуры, у которых площади равны, называют равновеликими. 2. Если фигура F составлена из фигур F 1,F 2,F 3,…, F n, то численное значение площади фигуры F равно сумме численных значений площадей фигур F 1,F 2,F 3,…, F n (при одной и той же единице площади).
Слайд 19
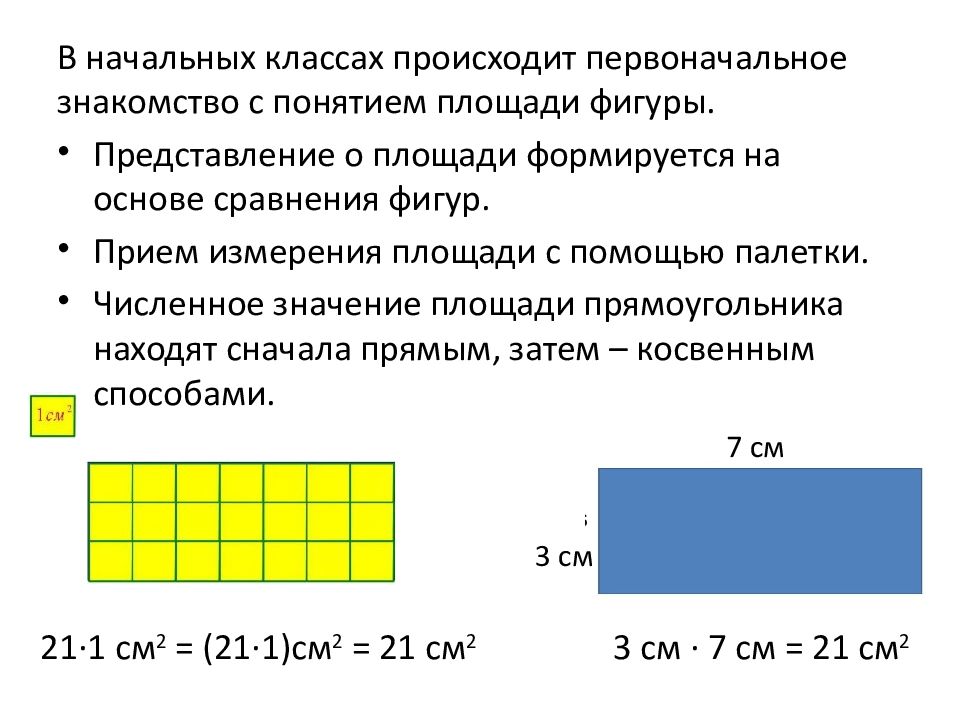
В начальных классах происходит первоначальное знакомство с понятием площади фигуры. Представление о площади формируется на основе сравнения фигур. Прием измерения площади с помощью палетки. Численное значение площади прямоугольника находят сначала прямым, затем – косвенным способами. 3 см 7 см 21·1 см 2 = (21·1)см 2 = 21 см 2 3 c м · 7 см = 21 см 2
Слайд 20
3. При замене единицы площади численное значение площади увеличивается (уменьшается) во столько раз, во сколько новая единица меньше (больше) старой. Например: 5 см 2 = … дм 2 1 см 2 = 0,01 дм 2 5 см 2 = 5 · 1 см 2 = 5 ·(0,01 дм 2 ) = (5·0,01)дм 2 = 0,05 дм 2
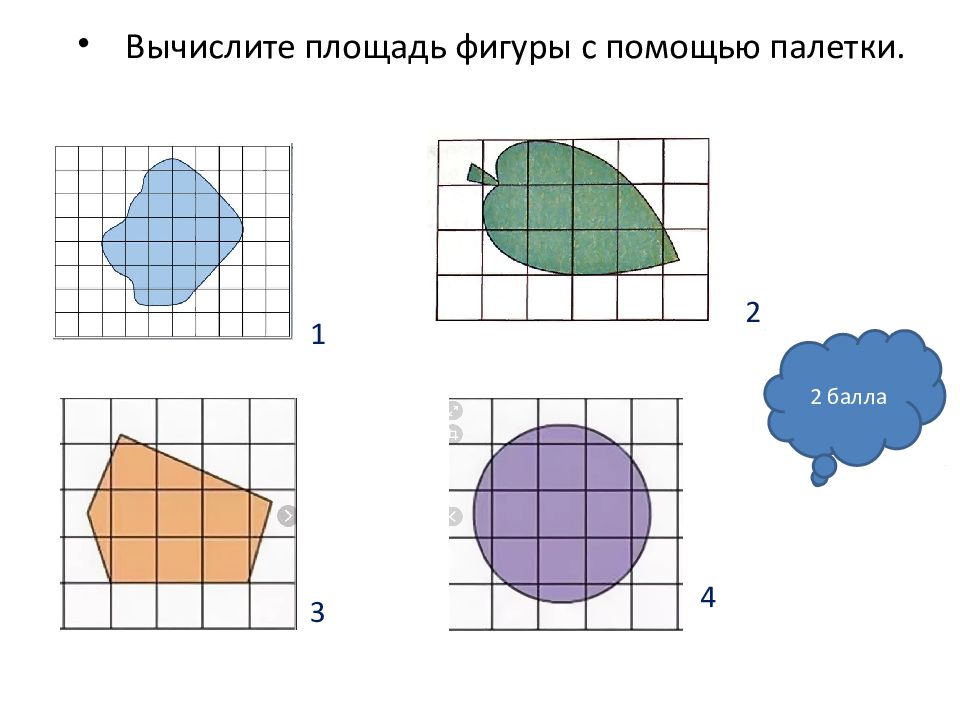
Слайд 21: Прием измерения площади фигуры с помощью палетки
Наложив палетку на фигуру определяем: число квадратов, которые целиком лежат внутри фигуры ( m) ; число квадратов, через которые проходит контур фигуры (n) S(F) ) е 2
Слайд 23
Среди следующих высказываний укажите истинные: Числовые значения площади одной и той же фигуры могут быть различны. Числовые значения площадей неравных фигур могут быть равными. Равновеликие фигуры равны.
Слайд 24: Масса – одна из основных физических величин
Масса – это такая положительная величина, которая обладает свойствами: масса одинакова у тел, уравновешивающих друг друга на весах; масса складывается, когда тела соединяются вместе: масса нескольких тел, взятых вместе, равна сумме их масс. Масса задана на множестве физических тел. Основная единица массы – килограмм.
Слайд 26: Измерение длины
300 см = мм 40 дм = см 23 м = см 4 км = дм 265 см = мм 40 дм = мм 23 м = дм 4 км = м
Слайд 28: Измерение массы
30 г = мг 5 кг = г 12 ц = кг 6 т = кг 78 г = мг 674 кг = ц кг 15 т = ц 3214 кг = т ц кг
Слайд 30: Сложение величин
100км 800м + 600м = 17см + 90мм = 53дм 2см + 286см = 41т + 94ц = 120мм + 14см = 18т 7ц+3ц =
Слайд 31: Вычитание величин
5 кг - 4кг 130г = 40т - 150ц = 7дм - 7см = 3кг 600г - 1515г = 9см 8мм - 84мм = 13м - 50дм =
Слайд 32: Задача
Петух в 2 раза легче утки и на 49кг 500г легче барана. Какова масса утки, если масса барана равна 52 килограммам? Какова общая масса петуха, барана и утки?