Задача. Построить минимальное остовное дерево (кратчайшую связывающую сеть) – соединение всех узлов сети с помощью путей наименьшей длины.
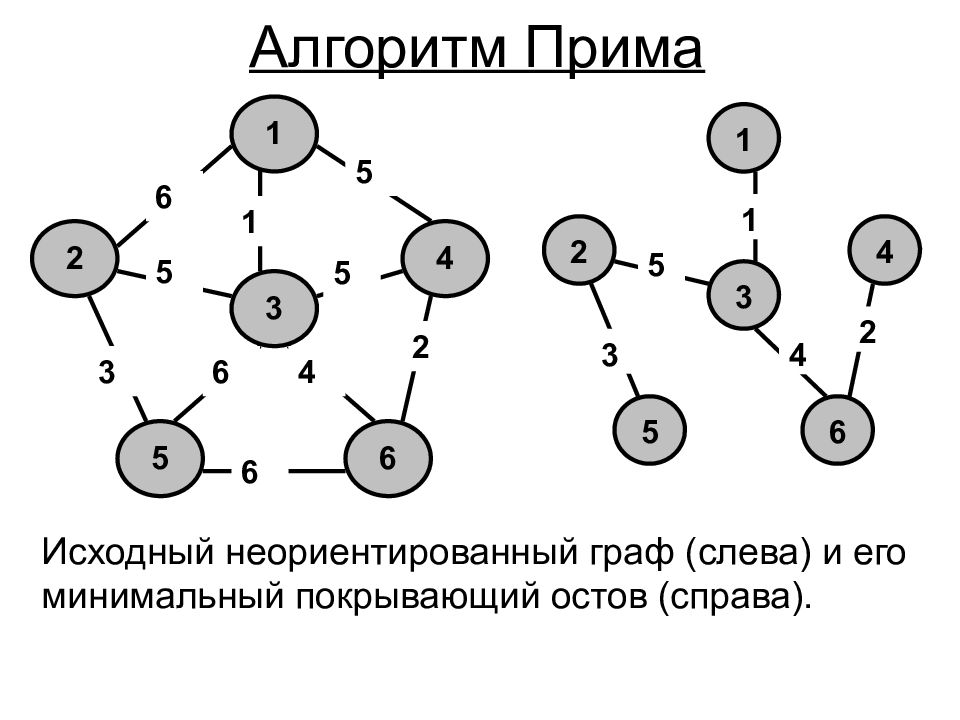
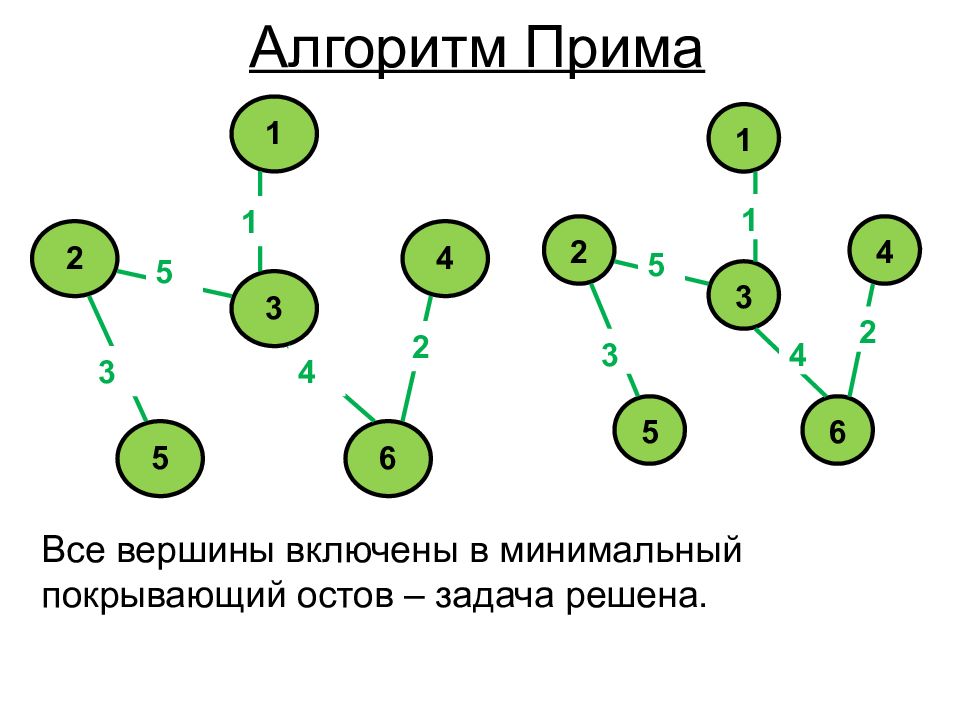
1 4 6 5 2 3 5 2 5 1 6 5 6 4 6 3 1 4 6 5 2 3 5 4 3 2 1 Исходный неориентированный граф (слева) и его минимальный покрывающий остов (справа). Алгоритм Прима
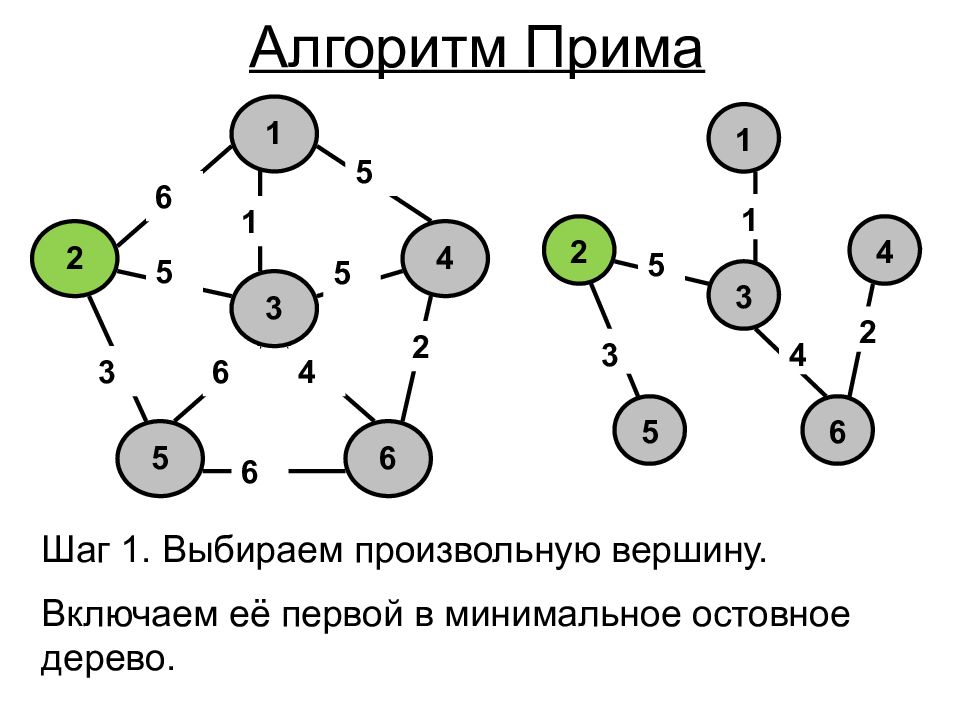
1 4 6 5 2 3 5 2 5 1 6 5 6 4 6 3 1 4 6 5 2 3 5 4 3 2 1 Шаг 1. Выбираем произвольную вершину. Включаем её первой в минимальное остовное дерево. Алгоритм Прима
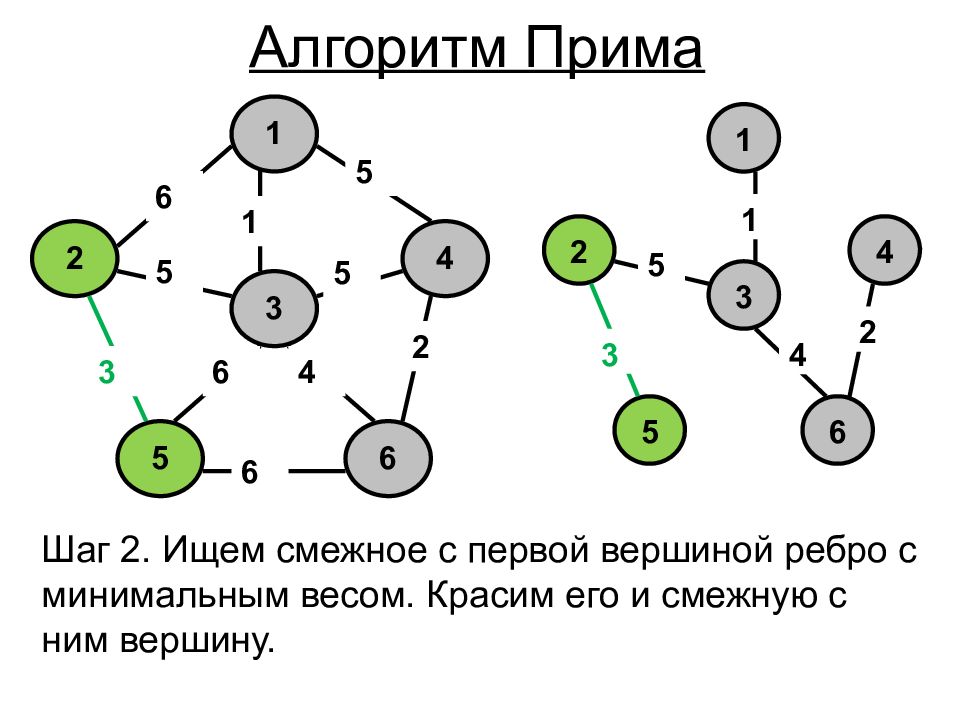
1 4 6 5 2 3 5 2 5 1 6 5 6 4 6 3 1 4 6 5 2 3 5 4 3 2 1 Шаг 2. Ищем смежное с первой вершиной ребро с минимальным весом. Красим его и смежную с ним вершину. Алгоритм Прима
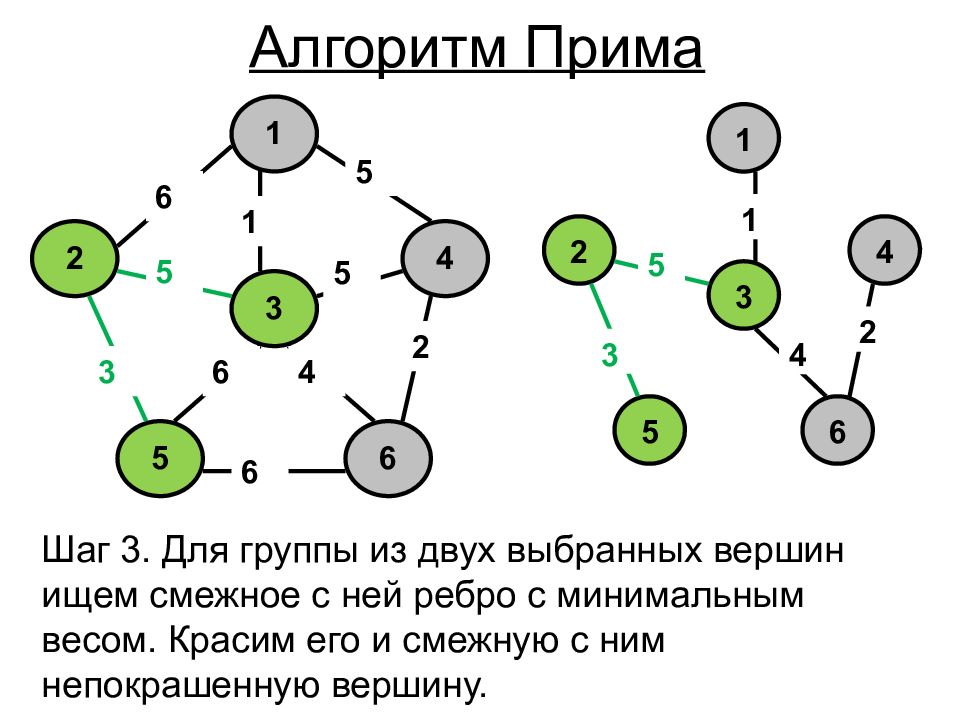
1 4 6 5 2 3 5 2 5 1 6 5 6 4 6 3 1 4 6 5 2 3 5 4 3 2 1 Шаг 3. Для группы из двух выбранных вершин ищем смежное с ней ребро с минимальным весом. Красим его и смежную с ним непокрашенную вершину. Алгоритм Прима
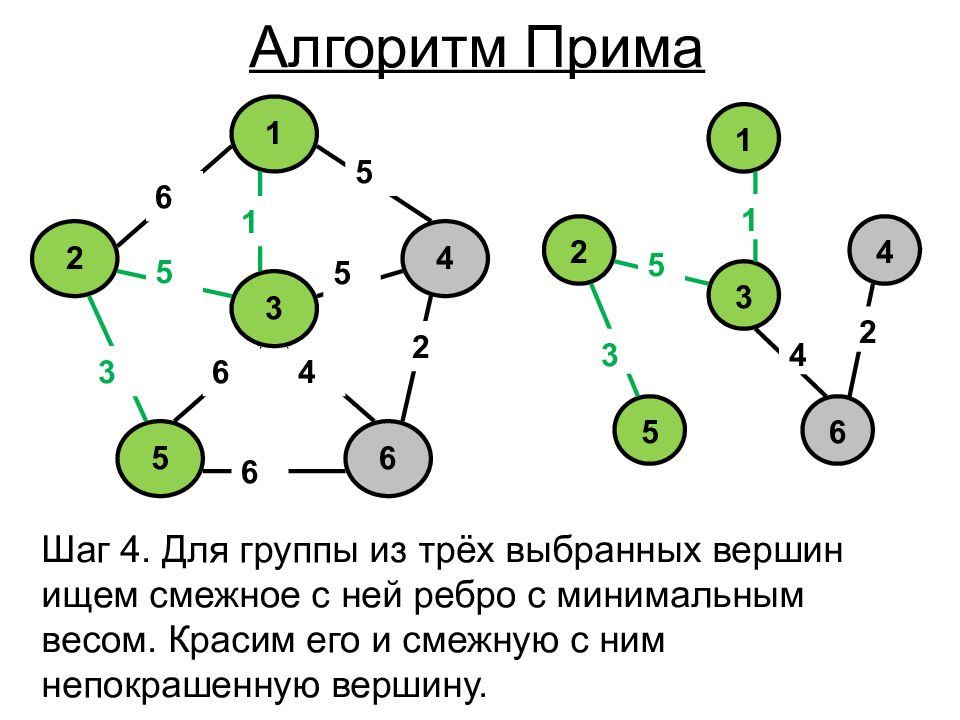
1 4 6 5 2 3 5 2 5 1 6 5 6 4 6 3 1 4 6 5 2 3 5 4 3 2 1 Шаг 4. Для группы из трёх выбранных вершин ищем смежное с ней ребро с минимальным весом. Красим его и смежную с ним непокрашенную вершину. Алгоритм Прима
1 4 6 5 2 3 5 2 5 1 6 5 6 4 6 3 1 4 6 5 2 3 5 4 3 2 1 Шаг 5. Для группы из четырёх выбранных вершин ищем смежное ребро с минимальным весом. Красим его и смежную с ним непокрашенную вершину. Алгоритм Прима
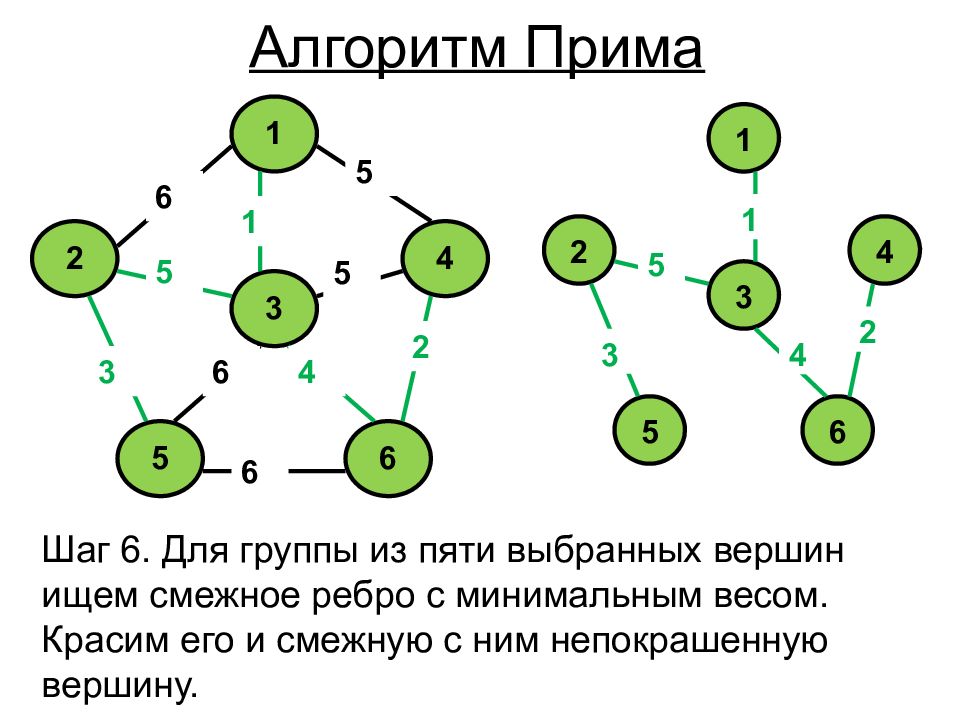
1 4 6 5 2 3 5 2 5 1 6 5 6 4 6 3 1 4 6 5 2 3 5 4 3 2 1 Шаг 6. Для группы из пяти выбранных вершин ищем смежное ребро с минимальным весом. Красим его и смежную с ним непокрашенную вершину. Алгоритм Прима
1 4 6 5 2 3 2 1 5 4 3 1 4 6 5 2 3 5 4 3 2 1 Все вершины включены в минимальный покрывающий остов – задача решена. Алгоритм Прима
