Первый слайд презентации: ЗАКОНЫ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНЫХ ВЕЛИЧИН
Слайд 2
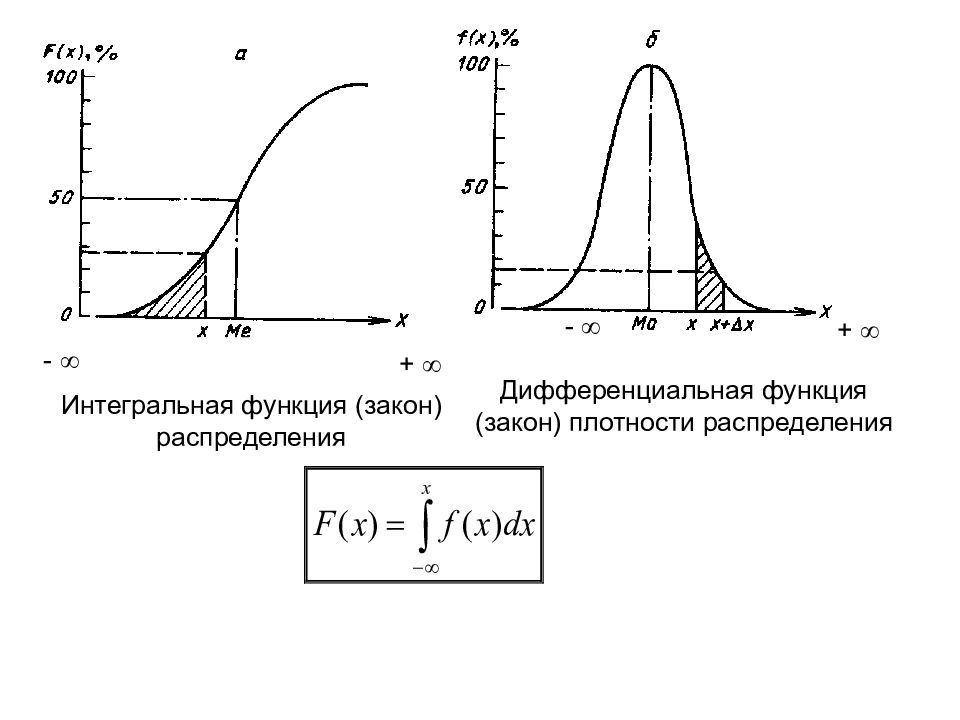
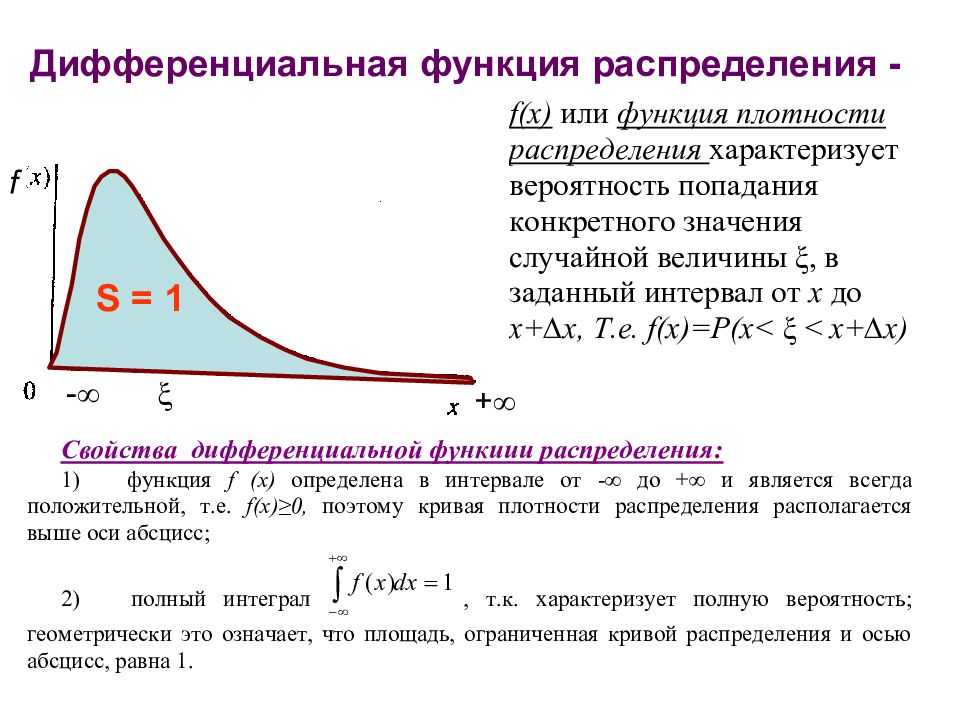
Дифференциальная функция (закон) плотности распределения Интегральная функция (закон) распределения + - - +
Слайд 4
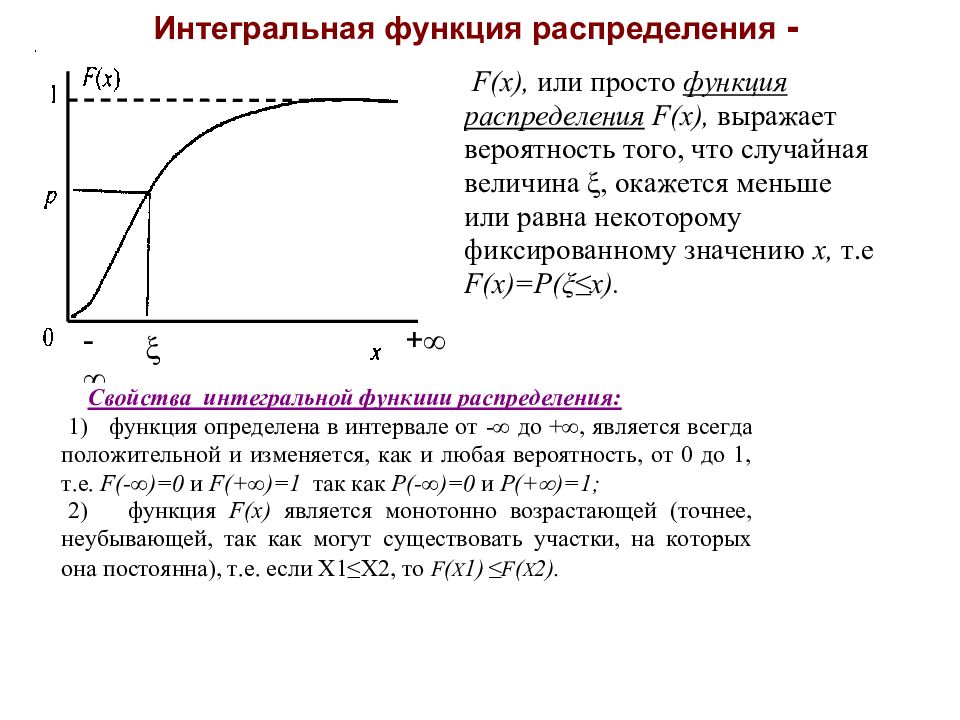
Интегральная функция распределения + - Ме для непрерывных величин для дискретных величин
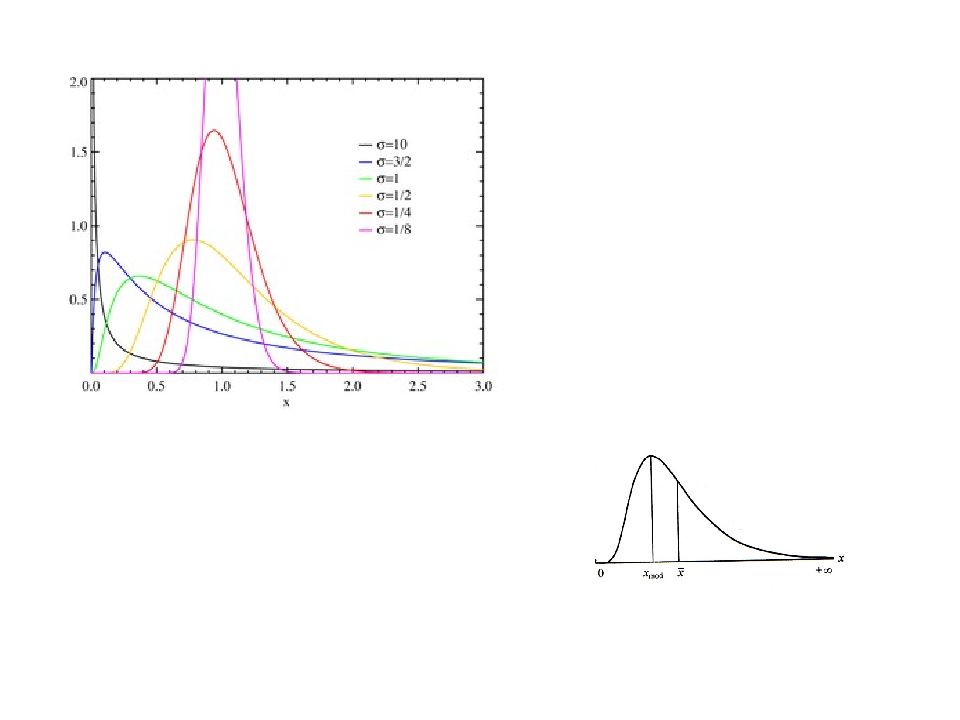
Слайд 11: ТЕОРЕТИЧЕСКИЕ РАСПРЕДЕЛЕНИЯ В ГЕОЛОГИИ
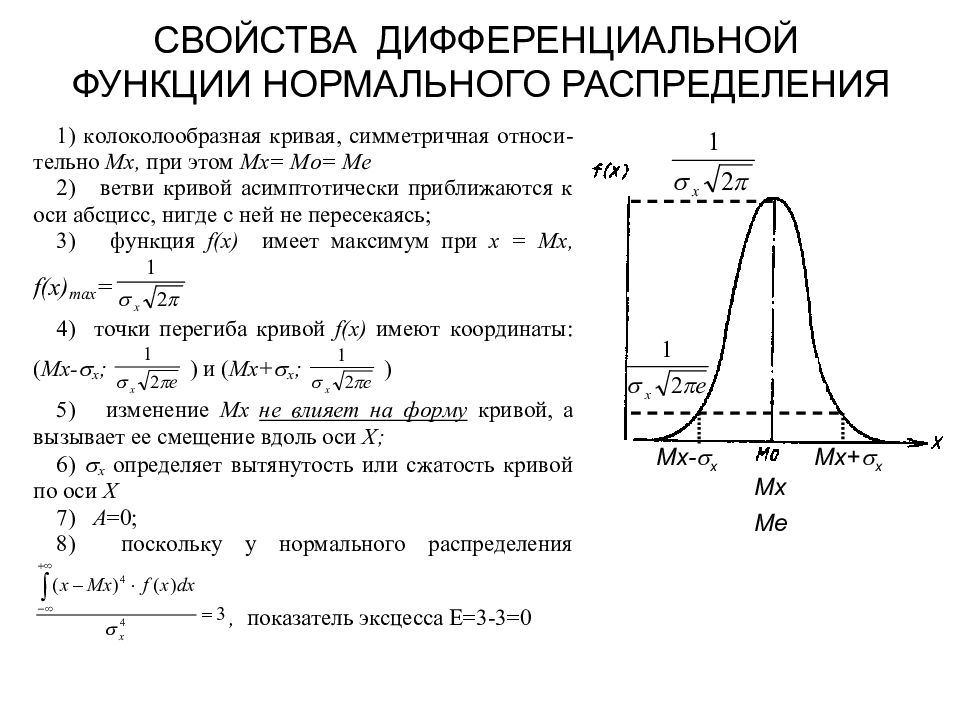
Слайд 13: СВОЙСТВА ДИФФЕРЕНЦИАЛЬНОЙ ФУНКЦИИ НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ
Мх Ме Мх- х Мх+ х
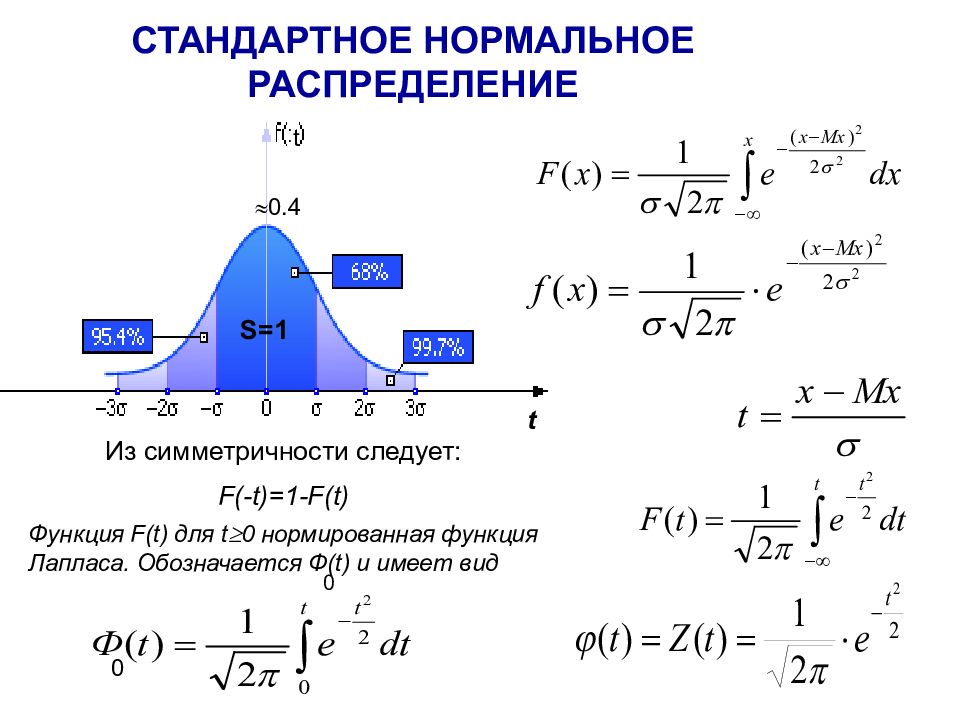
Слайд 15: СТАНДАРТНОЕ НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
Из симметричности следует: F(-t)=1-F(t) Функция F ( t ) для t 0 нормированная функция Лапласа. Обозначается Ф( t ) и имеет вид t t 0 0 0.4 S=1
Слайд 16
Z = (Х – μ )/ σ Любую нормально распределенную случайную величину X можно преобразовать в нормированную нормально распределенную случайную величину Z или t. Математическое ожидание стандартизованного нормального распределения равно нулю, а стандартное отклонение — единице. Плотность стандартизованного нормального распределения -6 -4 -2 0 2 4 6