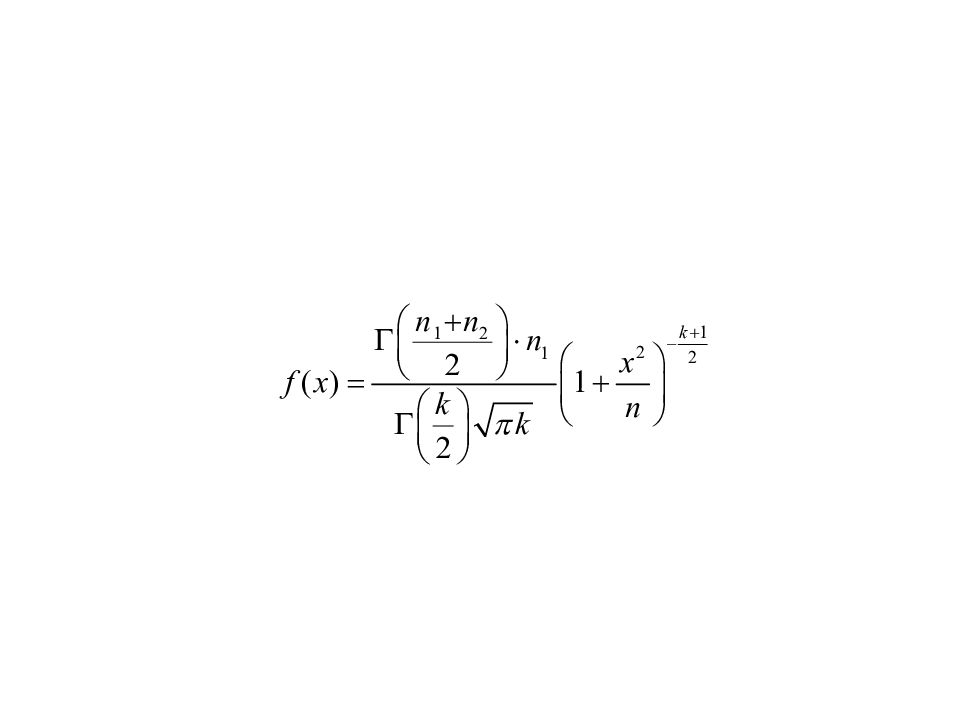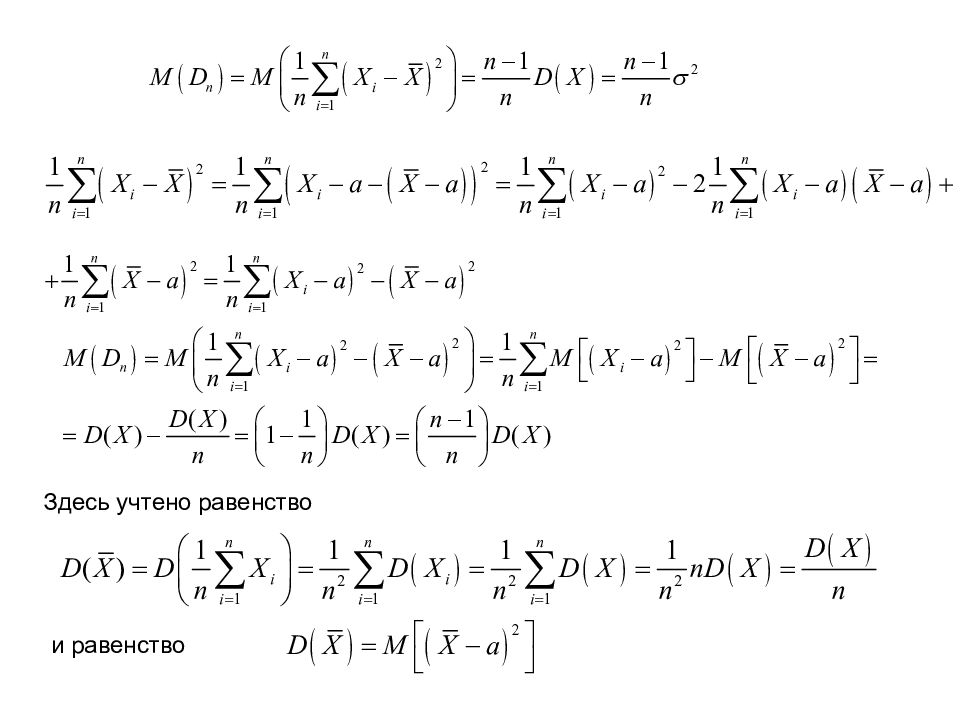1. Понятие о законе больших чисел. Теорема Чебышева. Теорема Бернулли. 2. Центральная предельная теорема теории вероятностей. Интегральная и локальная теоремы Муавра-Лапласа. Законы распределения, связанные с номальным: 4а) Распределение «хи-квадрат» 4б) распределение Стьюдента 4в)распределение Фишера Понятие о законе больших чисел. Теорема Чебышева. Теорема Бернулли Теорема Чебышева. Пусть X 1,X 2,X 3,…,X n - независимые случайные величины, m i =M(X i ), D i =D(X i ) ( i=1,2,…,n) – их математические ожидания и дисперсии, причем D i C. Тогда средняя арифметическая случайных величин при неограниченном увеличении n сходится к средней арифметической их математических ожиданий (с вероятностью сколь угодно мало отличающейся от единицы): Лекция 12
Теорема Бернулли. При неограниченном увеличении числа независимых испытаний относительная частота события W(A) сколь угодно мало отличается от вероятности события P(A) в единичном испытании (с вероятностью сколь угодно мало отличающейся от единицы): Замечание. Из теоремы Чебышева следует теорема Бернулли. Пусть X - число появлений события А в n независимых испытаниях, в каждом из которых и X i – число появлений события А в i- м испытании X i P i 0 1 q p
1 0,5 0,25 p D i 2. Це н тральная предельная теорема теории вероятностей Пусть X 1,X 2,…,X n - независимые случайные величины с произвольными законами распределения, m i =M(X i ), D i =D(X i ) – их математические ожидания и дисперсии. Если влияние каждой из них на сумму ничтожно мало, то случайная величина Y при имеет распределение, близкое к нормальному с параметрами и Это означает, что справедлива формула
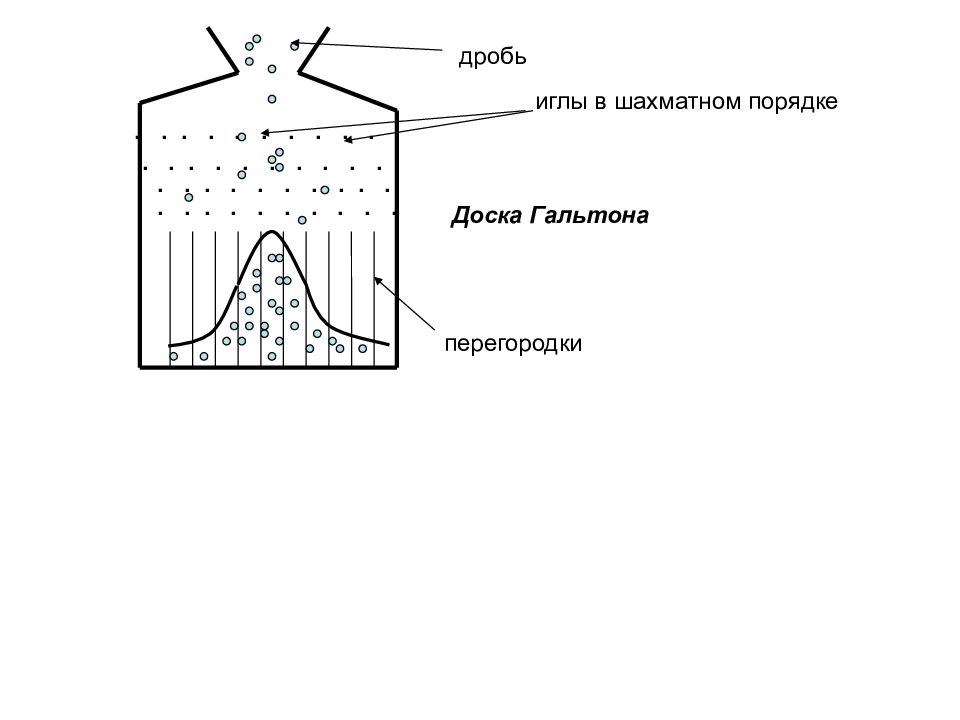
.......... .......... .......... .......... иглы в шахматном порядке дробь Доска Гальтона перегородки
Интегральная теорема Муавра-Лапласа Пусть X – число появлений события А в n независимых испытаниях, в каждом из которых P(A)=p, P( A )=1-p=q. При большом числе испытаний функция Лапласа Следует из центральной предельной теоремы.
Локальная теорема Муавра-Лапласа Пусть X – число появл е ний события А в n независимых испытаниях, в каждом из которых P(A)=p, P(A)=1-p=q. При большом числе испытаний Доказательство функция Гаусса
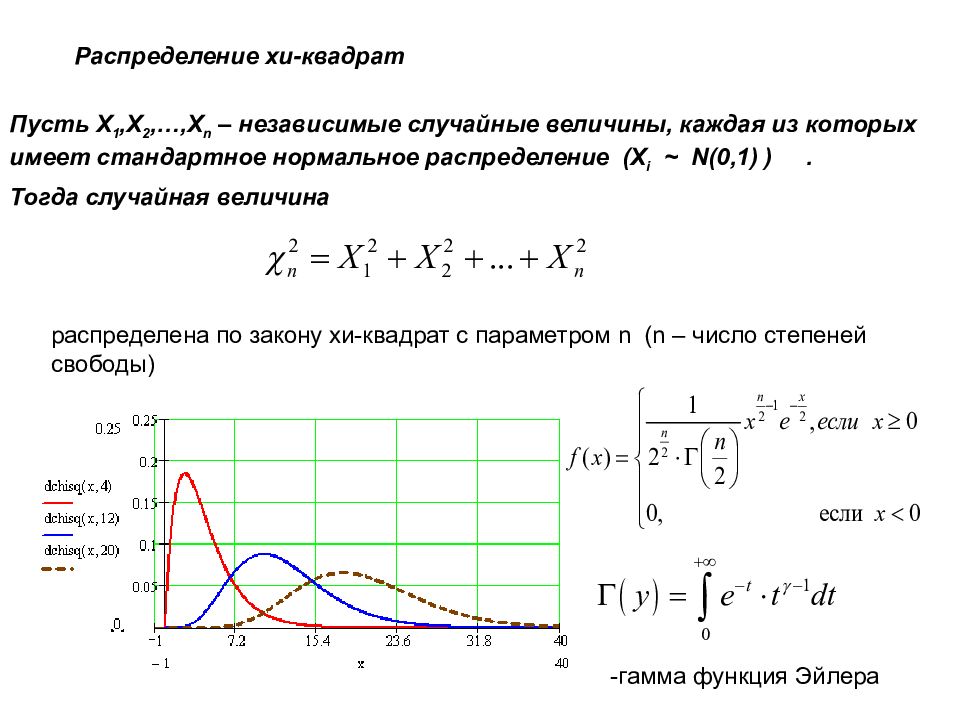
Распределение хи-квадрат Пусть X 1,X 2,…,X n – независимые случайные величины, каждая из которых имеет стандартное нормальное распределение ( X i ~ N(0,1) ). Тогда случайная величина распределена по закону хи-квадрат с параметром n ( n – число степеней свободы) -гамма функция Эйлера
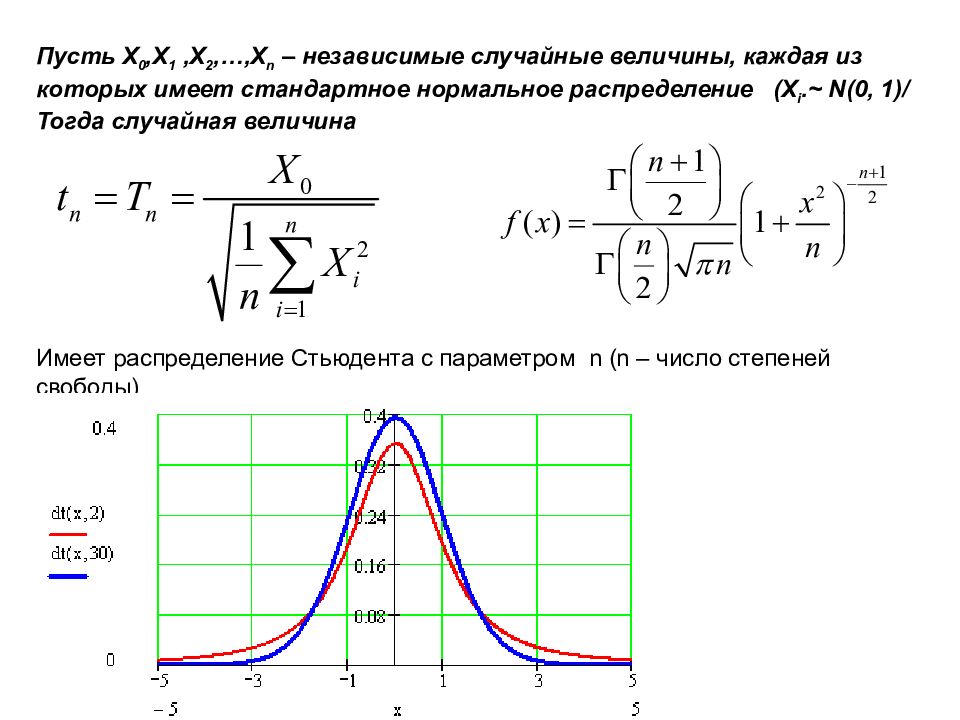
Пусть X 0, X 1,X 2,…,X n – независимые случайные величины, каждая из которых имеет стандартное нормальное распределение (X i. ~ N(0, 1)/ Тогда случайная величина Имеет распределение Стьюдента с параметром n (n – число степеней свободы)
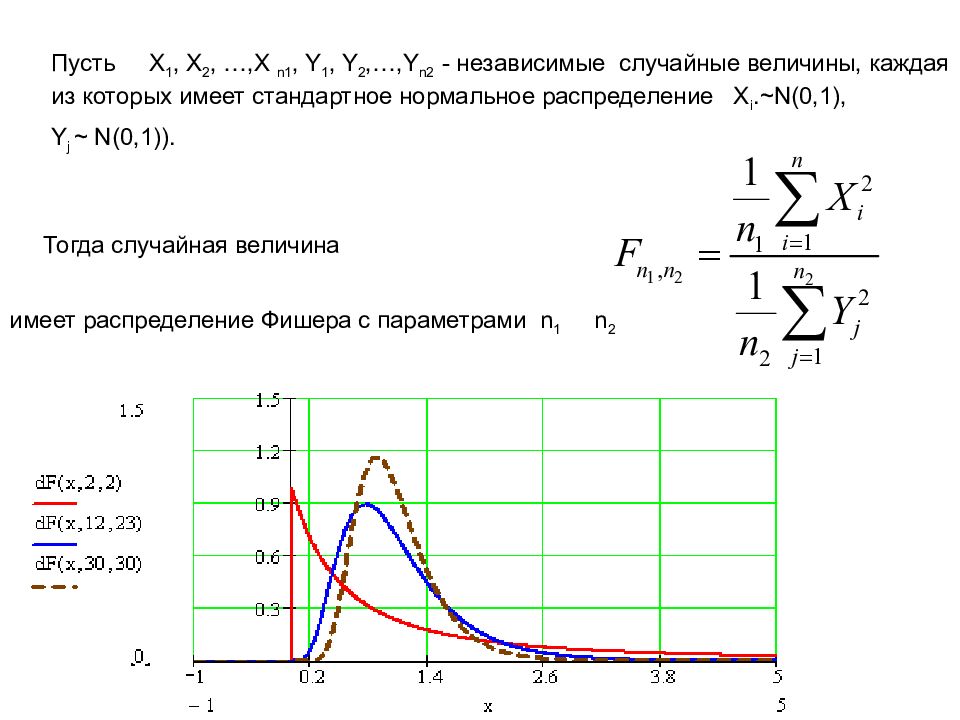
Пусть X 1, X 2, …,X n1, Y 1, Y 2,…,Y n2 - независимые случайные величины, каждая из которых имеет стандартное нормальное распределение X i. ~N(0,1), Y j ~ N(0,1)). Тогда случайная величина имеет распределение Фишера с параметрами n 1 n 2
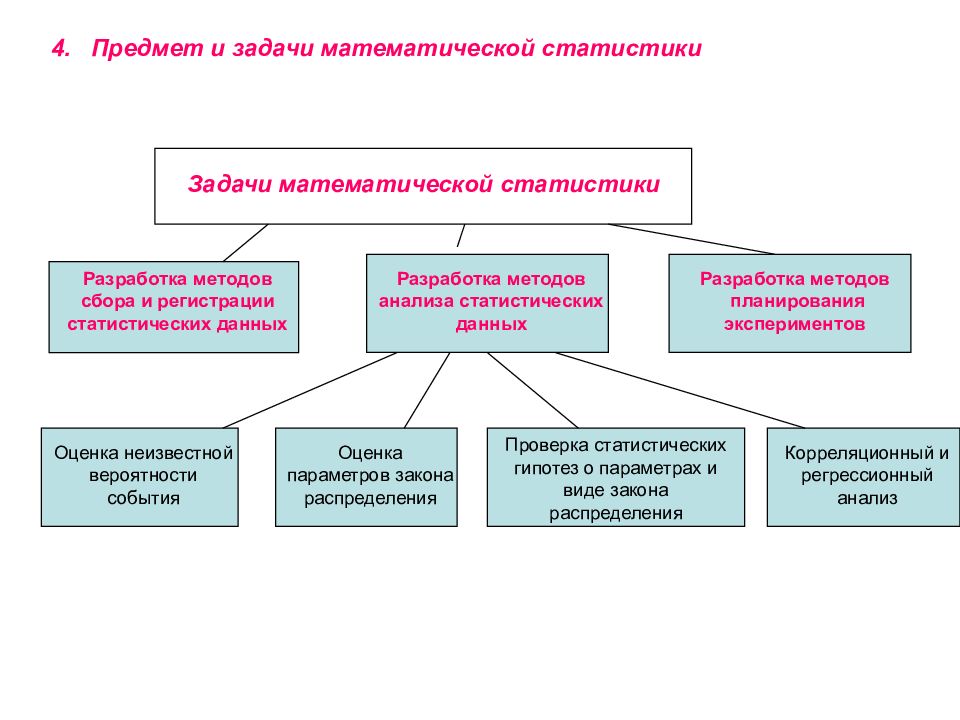
4. Предмет и задачи математической статистики Задачи математической статистики Разработка методов сбора и регистрации статистических данных Разработка методов анализа статистических данных Разработка методов планирования экспериментов Оценка неизвестной вероятности события Оценка параметров закона распределения Проверка статистических гипотез о параметрах и виде закона распределения Корреляционный и регрессионный анализ
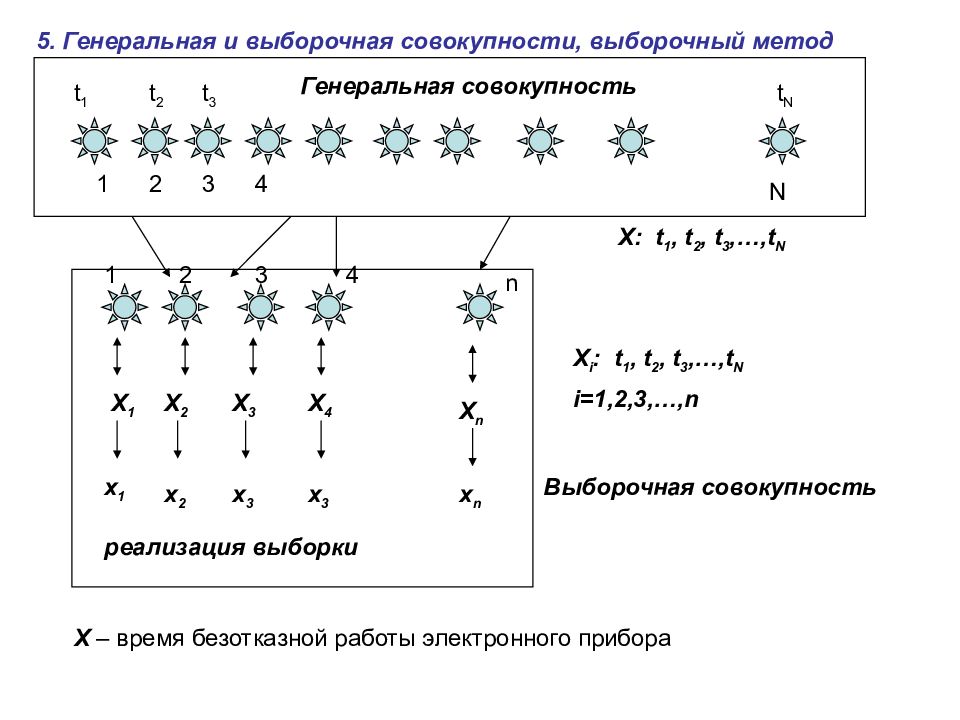
5. Генеральная и выборочная совокупности, выборочный метод 1 1 2 n 3 4 t 1 t 3 t 2 t N 4 3 2 N X: t 1, t 2, t 3,…,t N Генеральная совокупность X 1 X 2 X 3 X 4 X n X i : t 1, t 2, t 3,…,t N i=1,2,3,…,n x 1 x 2 x 3 x 3 x n реализация выборки X – время безотказной работы электронного прибора Выборочная совокупность
Вероятностная модель выборки Определение. Последовательность n независимых случайных величин X 1,X 2,…,X n, распределение каждой из которых совпадает с распределением исследуемой случайной величины X, называют случайной выборкой
1. Статистическое распределение выборки. Полигон и гистограмма Пусть x 1,x 2,…,x n – реализация выборки Ряд значений признака в выборке, расположенных в порядке возрастания называется ранжированным (или вариационным) рядом Различные значения x (i) признака в выборке называют вариантами ( i=1,2,..,k ) Количество n i повторений варианты x (i) в выборке называют её частотой Величина называется относительной частотой варианты x (i) Соответствие между значениями признака в выборке и их частотами (или относительными частотами) называется статистическим распределением выборки.
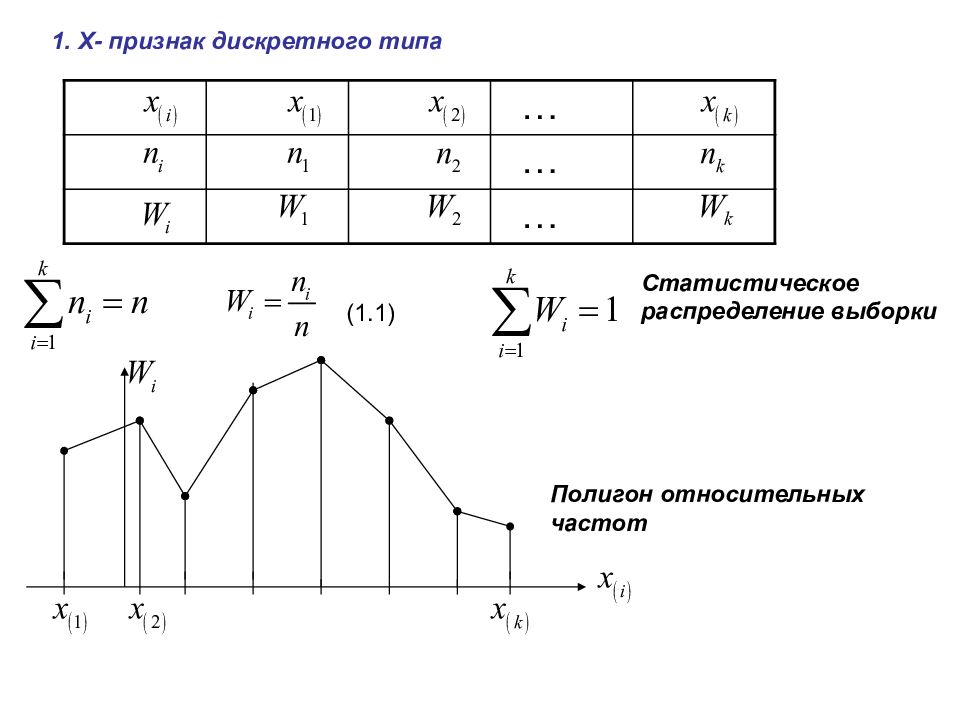
1. Х- признак дискретного типа … … … Статистическое распределение выборки Полигон относительных частот (1.1)
Пример. Дана выборка (значение выборки): 2,1; 5; 5; 3; 3; 4,2; 3; 4,2; 4,2; 3 Построить статистическое распределение выборки. Ранжированный ряд: 2,1; 3; 3; 3; 3; 4,2; 4,2; 4,2; 5; 5 Варианты, их частоты и относительные частоты: 2 3 4 5 1 4 3 2 0,1 0,4 0,3 0,2 0,2 0,4 Решение. 4 5 2 3 Статистическое распределение выборки Полигон относительных частот
x 1, x 2, x 3,…, x n 2. Х – признак непрерывного типа - реализация выборки - размах выборки Формула Стерджеса Интервальное распределение выборки … n i n 1 n 2 … n k W i W 1 W 2 … W k p i p 1 p 2 p k относительная частота - плотность относительной частоты - длина частичного интервала (1.2) (1.3) (1.4)
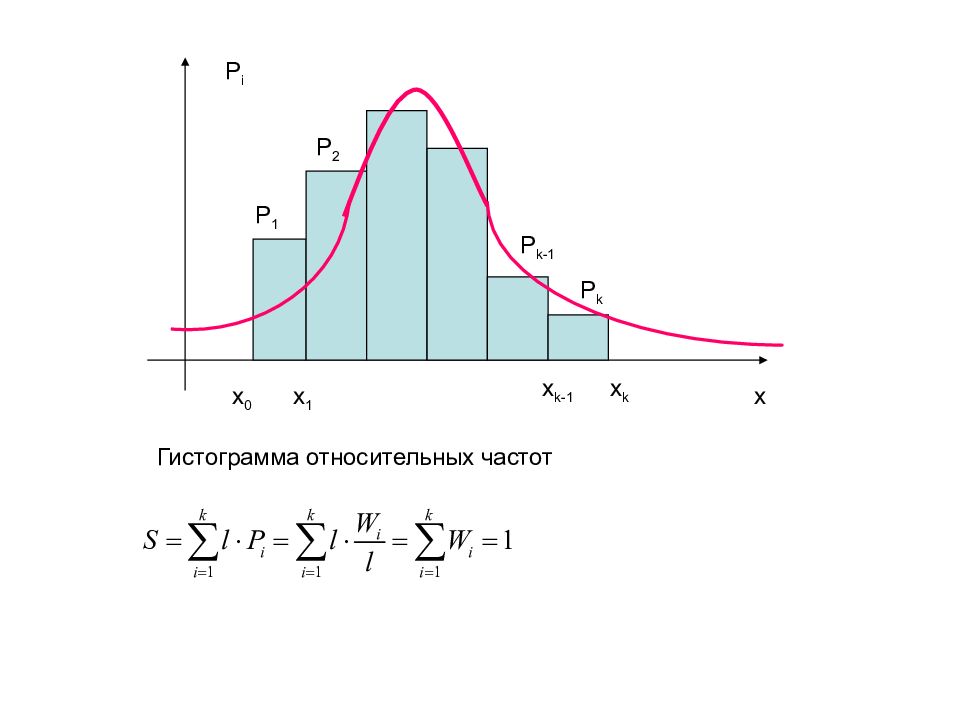
P i x x 0 P 1 P 2 P k-1 P k x 1 x k-1 x k Гистограмма относительных частот
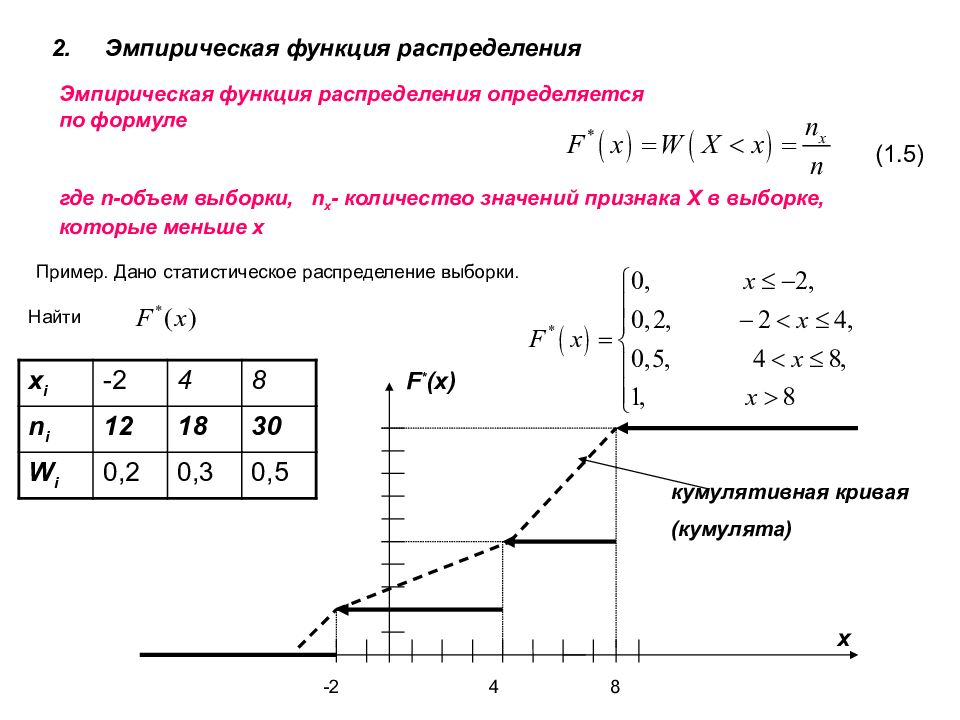
2. Эмпирическая функция распределения где n- объем выборки, n x - количество значений признака X в выборке, которые меньше x x i -2 4 8 n i 12 18 30 W i 0,2 0,3 0,5 F * (x) x Эмпирическая функция распределения определяется по формуле -2 4 8 (1.5) Пример. Дано статистическое распределение выборки. Найти кумулятивная кривая (кумулята)
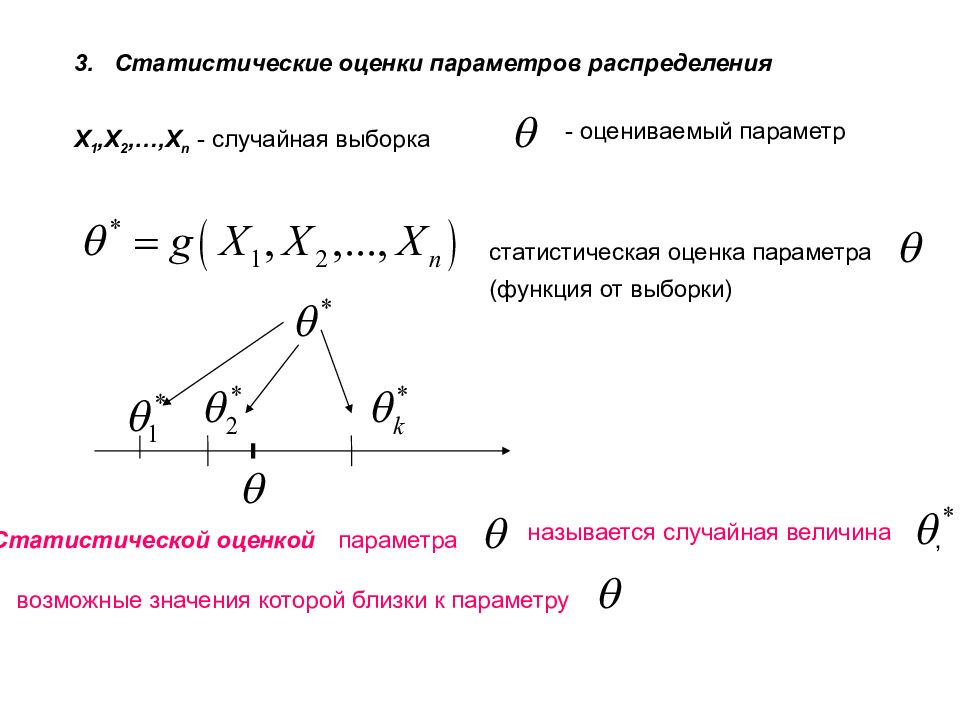
3. Статистические оценки параметров распределения Х 1, X 2,…,X n - случайная выборка - оцениваемый параметр статистическая оценка параметра (функция от выборки) Статистической оценкой параметра возможные значения которой близки к параметру называется случайная величина ,
Статистическая оценка называется несмещенной, если ее математическое ожидание равно оцениваемому параметру при любом объеме выборки, т.е. В противном случае оценка называется смещенной. Статистическая оценка называется эффективной, если она имеет наименьшую дисперсию при заданном объеме выборке Статистическая оценка называется состоятельной, если при она сходится по вероятности к оцениваемому параметру, т.е.
4. Выборочная средняя - оценка математического ожидания Пусть Х – исследуемый признак, X 1,X 2,…,X n – случайная выборка Тогда Выборочная средняя определяется по формуле: Теорема. Выборочная средняя является несмещенной и состоятельной оценкой математического ожидания. (1.6) (1.7) Д.
Докажем состоятельность оценки. По теореме Чебышева Замечание. Выборочная средняя является также эффективной оценкой математического ожидания Выборочная дисперсия определяется по формуле Теорема. Выборочная дисперсия является смещенной оценкой дисперсии 5.Выборочная дисперсия. Исправленная выборочная дисперсия (1.8) (1.9)
Здесь учтено равенство и равенство
Исправленная выборочная дисперсия определяется по формуле: Исправленная выборочная дисперсия является несмещенной оценкой дисперсии Выборочное среднее квадратическое отклонение определяется по формуле: Исправленное выборочное среднее квадратическое отклонение : 6.Выборочное среднее квадратическое отклонение. Исправленное выборочное с.к.о. (1.10) (1.11) (1.12)
Замечания. 1. Справедлива формула Здесь
2. Задано статистическое распределение выборки … … …
