Первый слайд презентации: Определители, их вычисление и свойства
1 § Определители, их вычисление и свойства 1. Понятие определителя Определителем порядка n квадратной матрицы n - го порядка называют число, соответствующее этой квадратной матрице. Определитель числовой матрицы первого порядка равен числу, являющемуся элементом этой матрицы.
Слайд 2
2 Определитель матрицы A обозначают | A|, det A или Элементы, строки, столбцы матрицы называются соответственно элементами, строками, столбцами определителя матрицы.
3 Определитель второго порядка равен разности произведений элементов главной диагонали и элементов побочной диагонали
4 Вычисление определителя третьего порядка
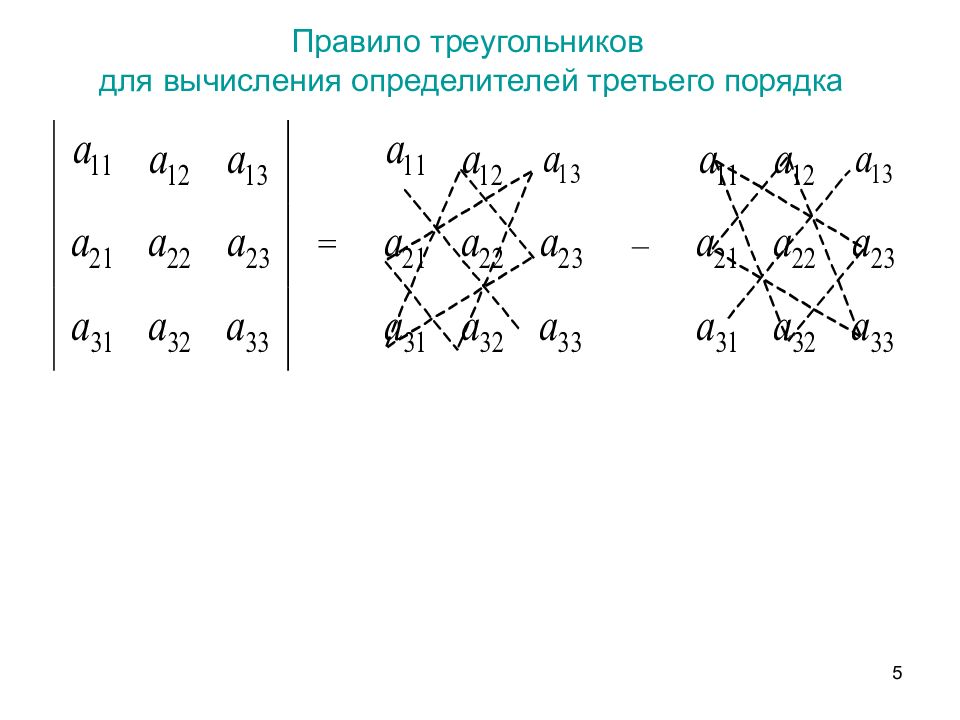
Слайд 5: Правило треугольников для вычисления определителей третьего порядка
5 Правило треугольников для вычисления определителей третьего порядка
Слайд 6: Определитель треугольного вида равен произведению элементов главной диагонали
6 Определитель треугольного вида равен произведению элементов главной диагонали
7 § Системы линейных уравнений 1. Основные понятия Уравнение называется линейным, если неизвестные в нём содержатся только в первой степени и между собой не перемножаются, т.е. если оно имеет вид, где a i, b – известные заданные числа, - неизвестные уравнения. a i называются коэффициентами уравнения, b называется свободным членом. Если b = 0, то уравнение называется однородным. Если, уравнение называется неоднородным.
Слайд 8: Рассмотрим систему m линейных уравнений с n неизвестными, т.е. систему вида
8 Рассмотрим систему m линейных уравнений с n неизвестными, т.е. систему вида
Слайд 9: Обозначим через A и A* следующие матрицы:
9 Обозначим через A и A* следующие матрицы: Матрицу A называют основной матрицей системы (1), матрицу A* – расширенной матрицей системы (1). Пусть X – матрица-столбец неизвестных, B – матрица-столбец свободных членов, т.е. Тогда систему (1) можно записать в виде матричного уравнения AX=B. Его называют матричной формой системы (1).
Слайд 10: 2. Методы решения систем линейных уравнений
10 2. Методы решения систем линейных уравнений Матричный метод. ОПРЕДЕЛЕНИЕ. Обратной к матрице A называется матрица, обозначаемая A -1, такая, что A·A -1 =A -1 · A=E. Преобразование матричных уравнений Квадратная матрица, определитель которой отличен от нуля, называется невырожденной.
Слайд 11: ТЕОРЕМА. Пусть A – квадратная матрица. Матрица A имеет обратную тогда и только тогда, когда её определитель | A| отличен от нуля
11 ТЕОРЕМА. Пусть A – квадратная матрица. Матрица A имеет обратную тогда и только тогда, когда её определитель | A| отличен от нуля. Нахождение решения AX=B по формуле называют матричным методом решения системы.
Слайд 12: Пример
12 Пример Решить систему уравнений матричным методом. Решение. Проверка!!!
Слайд 13: Метод Крамера
13 Метод Крамера ТЕОРЕМА (Крамера). Если в системе линейных уравнений число уравнений m и число неизвестных n совпадает, и |A| 0, то система совместна и имеет единственное решение, которое может быть найдено по формулам где D =|A|, а – определитель, получаемый из определителя D заменой его i -го столбца на столбец свободных членов. Формулы называются формулами Крамера.