1 Упрощение логических выражений Шаг 1. Заменить операции на их выражения через И, ИЛИ и НЕ : Шаг 2. Раскрыть инверсию сложных выражений по формулам де Моргана: Шаг 3. Используя законы логики, упрощать выражение, стараясь применять закон исключения третьего.
2 Упрощение логических выражений раскрыли формула де Моргана распределительный исключения третьего повторения поглощения
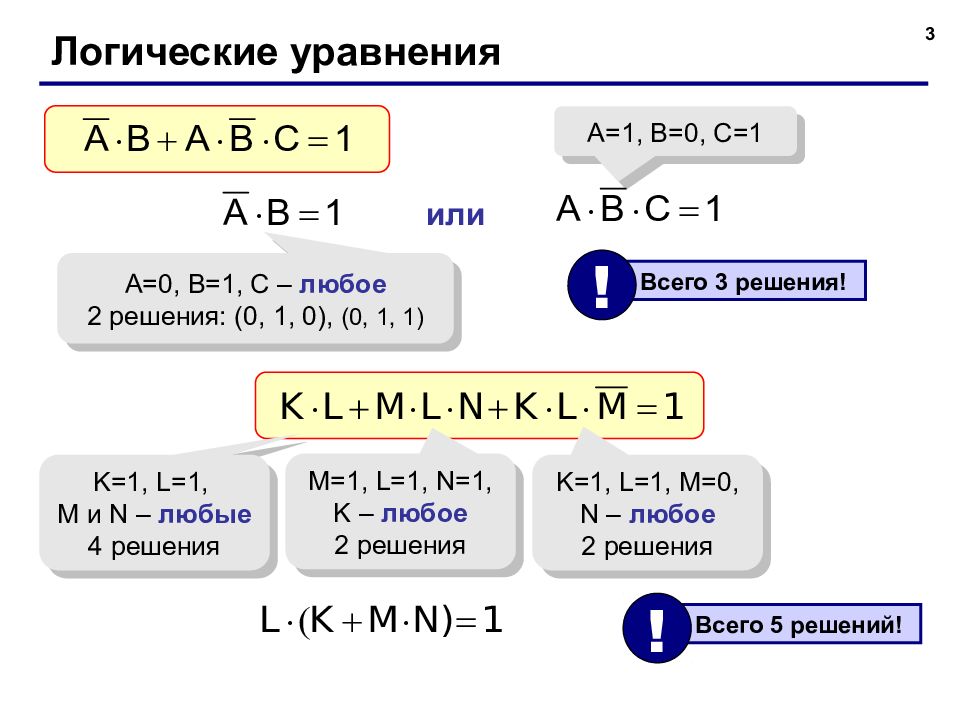
3 Логические уравнения A=0, B=1, C – любое 2 решения: (0, 1, 0), (0, 1, 1) или A= 1, B= 0, C =1 Всего 3 решения! ! K= 1, L=1, M и N – любые 4 решения M=1, L=1, N=1, K – любое 2 решения K=1, L=1, M=0, N – любое 2 решения Всего 5 решений! !
4 Как построить логическую формулу Синтез логических выражений
Совершенная Дизъюнктивная Нормальная форма (СДНФ) Формулу называют элементарной конъюнкцией, если она является конъюнкцией переменных или их отрицаний без повторения Формула называется дизъюнктивной нормальной формой (ДНФ), если она является дизъюнкцией неповторяющихся элементарных конъюнкций. Формула называется совершенной дизъюнктивной нормальной формой (СДНФ), если: 1) она является ДНФ 2) В каждую элементарную конъюнкцию входят все переменные (или их отрицания), от которых зависит функция
1. В таблице истинности отмечаем наборы переменных, на которых значение функции F равно 1. 2. Записываем для каждого отмеченного набора конъюнкцию всех переменных следующим образом: если значение некоторой переменной в этом наборе равно 1, то в конъюнкцию включаем саму переменную, в противном случае — ее отрицание. 3. Все полученные конъюнкции связываем операциями дизъюнкции.
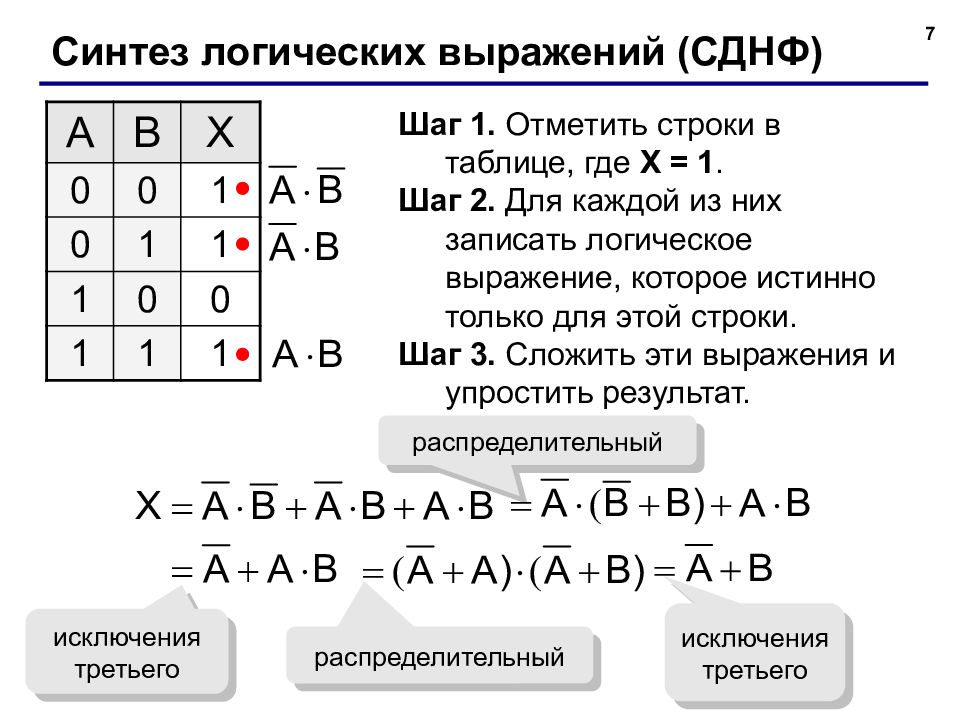
7 Синтез логических выражений (СДНФ) A B X 0 0 1 0 1 1 1 0 0 1 1 1 Шаг 1. Отметить строки в таблице, где X = 1. Шаг 2. Для каждой из них записать логическое выражение, которое истинно только для этой строки. Шаг 3. Сложить эти выражения и упростить результат. распределительный исключения третьего исключения третьего распределительный
8 Синтез логических выражений (СДНФ) A B C X 0 0 0 1 0 0 1 1 0 1 0 1 0 1 1 1 1 0 0 0 1 0 1 1 1 1 0 0 1 1 1 1
Совершенная Конъюнктивная Нормальная форма (СКНФ) Формулу называют элементарной дизъюнкцией, если она является дизъюнкцией переменных или их отрицаний без повторения Формула называется конъюнктивной нормальной формой (КНФ), если она является конъюнкцией неповторяющихся элементарных дизъюнкций. Формула называется совершенной конъюнктивной нормальной формой (СКНФ), если: 1) она является КНФ 2) В каждую элементарную дизъюнкцию входят все переменные (или их отрицания), от которых зависит функция
В таблице истинности отмечаем наборы переменных, на которых значение функции F равно 0. Записываем для каждого отмеченного набора дизъюнкцию всех переменных следующим образом: если значение некоторой переменной в этом наборе равно 0, то в конъюнкцию включаем саму переменную, в противном случае — ее отрицание. Все полученные дизъюнкции связываем операциями конъюнкции.
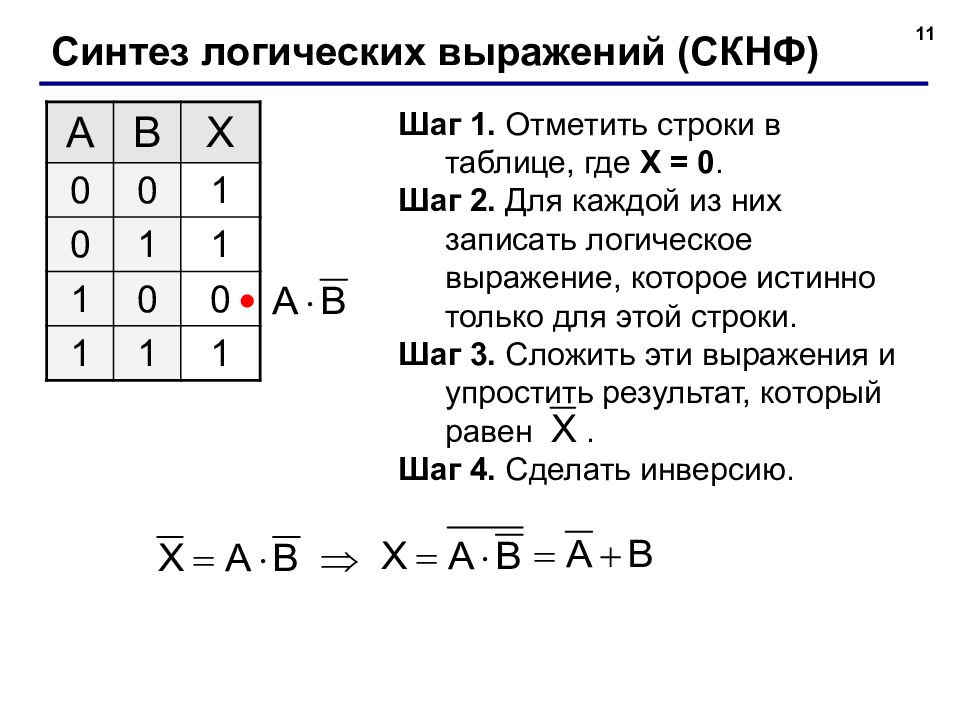
11 Синтез логических выражений (СКНФ) A B X 0 0 1 0 1 1 1 0 0 1 1 1 Шаг 1. Отметить строки в таблице, где X = 0. Шаг 2. Для каждой из них записать логическое выражение, которое истинно только для этой строки. Шаг 3. Сложить эти выражения и упростить результат, который равен. Шаг 4. Сделать инверсию.
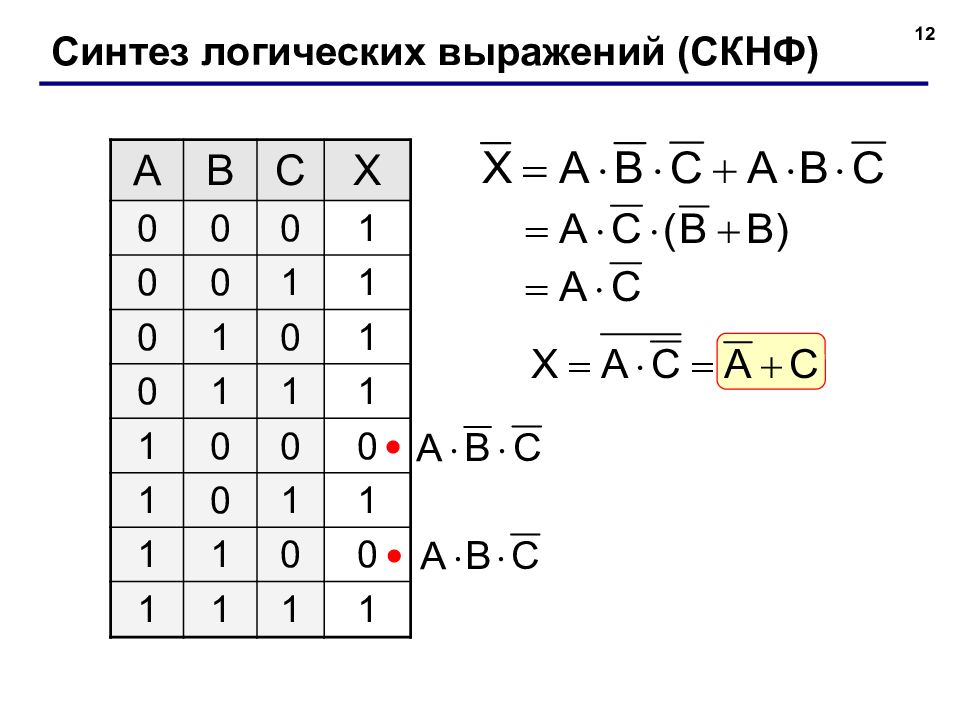
12 Синтез логических выражений ( СКНФ) A B C X 0 0 0 1 0 0 1 1 0 1 0 1 0 1 1 1 1 0 0 0 1 0 1 1 1 1 0 0 1 1 1 1
Найти логическую функцию F, зависящую от логических переменных A, B, C, по заданной таблице истинности. Упрощенный вид функции должен содержать не более трех логических операций. В упрощенном виде функции допустимо использовать только операции ИНВЕРСИЯ, КОНЪЮНКЦИЯ и ДИЗЪЮНКЦИЯ. A B C F 0 0 0 0 0 0 1 1 0 1 0 0 0 1 1 1 1 0 0 1 1 0 1 1 1 1 0 0 1 1 1 1
A B C F 0 0 0 0 0 0 1 1 0 1 0 0 0 1 1 1 1 0 0 1 1 0 1 1 1 1 0 0 1 1 1 1
A B C F 0 0 0 0 0 0 1 1 0 1 0 0 0 1 1 1 1 0 0 1 1 0 1 1 1 1 0 0 1 1 1 1 Способ 1б. Решение через СДНФ
A B C F 0 0 0 0 0 0 1 1 0 1 0 0 0 1 1 1 1 0 0 1 1 0 1 1 1 1 0 0 1 1 1 1
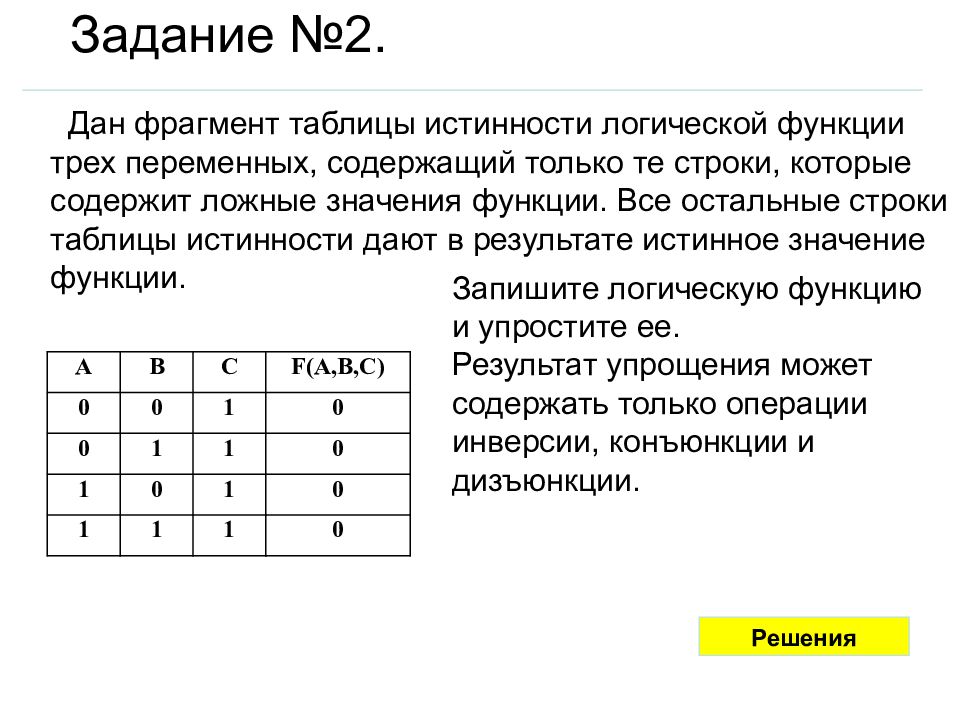
Дан фрагмент таблицы истинности логической функции трех переменных, содержащий только те строки, которые содержит ложные значения функции. Все остальные строки таблицы истинности дают в результате истинное значение функции. Запишите логическую функцию и упростите ее. Результат упрощения может содержать только операции инверсии, конъюнкции и дизъюнкции. А В С F(A,B,C) 0 0 1 0 0 1 1 0 1 0 1 0 1 1 1 0 Задание №2. Решения
Решение А В С F 0 0 1 0 0 1 1 0 1 0 1 0 1 1 1 0
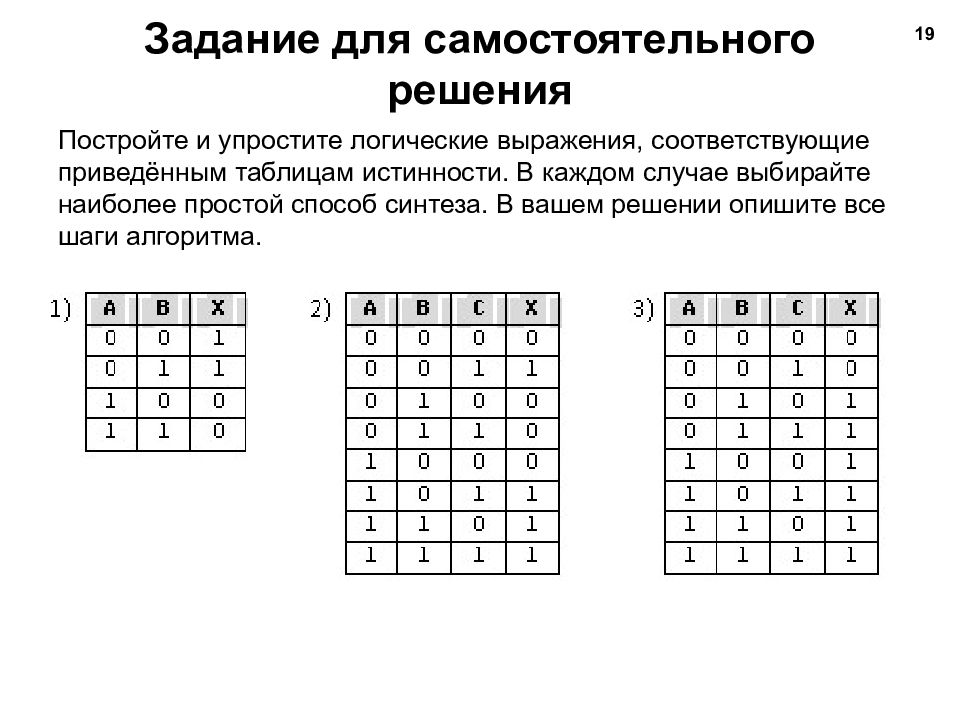
Постройте и упростите логические выражения, соответствующие приведённым таблицам истинности. В каждом случае выбирайте наиболее простой способ синтеза. В вашем решении опишите все шаги алгоритма. 19
