ЭЛЕМЕНТЫ АЛГЕБРЫ ЛОГИКИ МАТЕМАТИЧЕСКИЕ ОСНОВЫ ИНФОРМАТИКИ
Ключевые слова логическое выражение таблица истинности законы логики
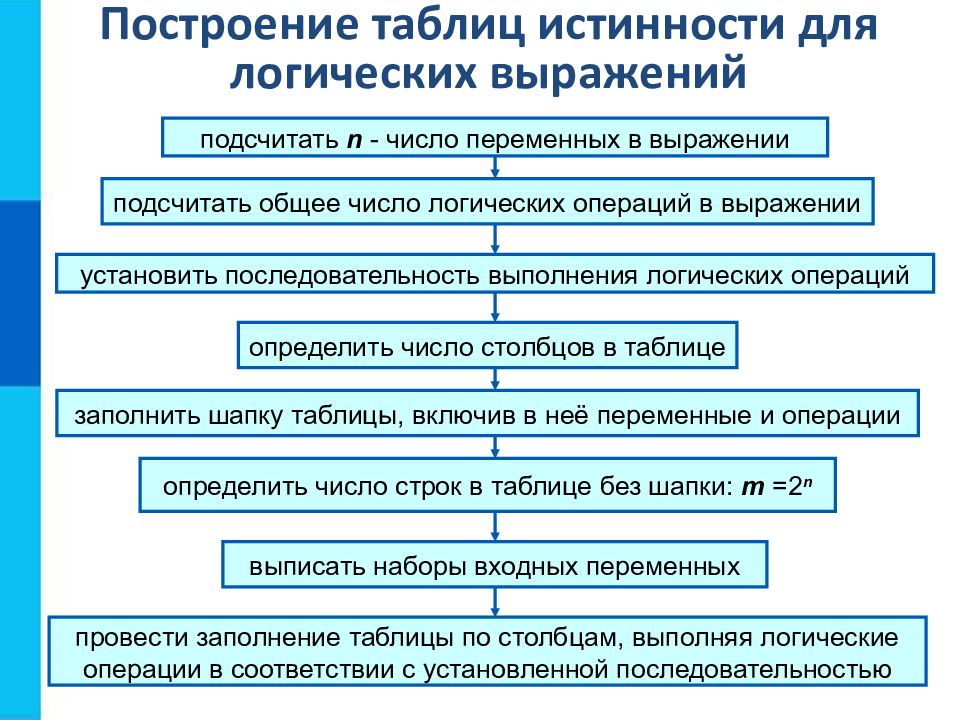
Построение таблиц истинности для логических выражений подсчитать n - число переменных в выражении подсчитать общее число логических операций в выражении установить последовательность выполнения логических операций определить число столбцов в таблице заполнить шапку таблицы, включив в неё переменные и операции определить число строк в таблице без шапки: m =2 n выписать наборы входных переменных провести заполнение таблицы по столбцам, выполняя логические операции в соответствии с установленной последовательностью
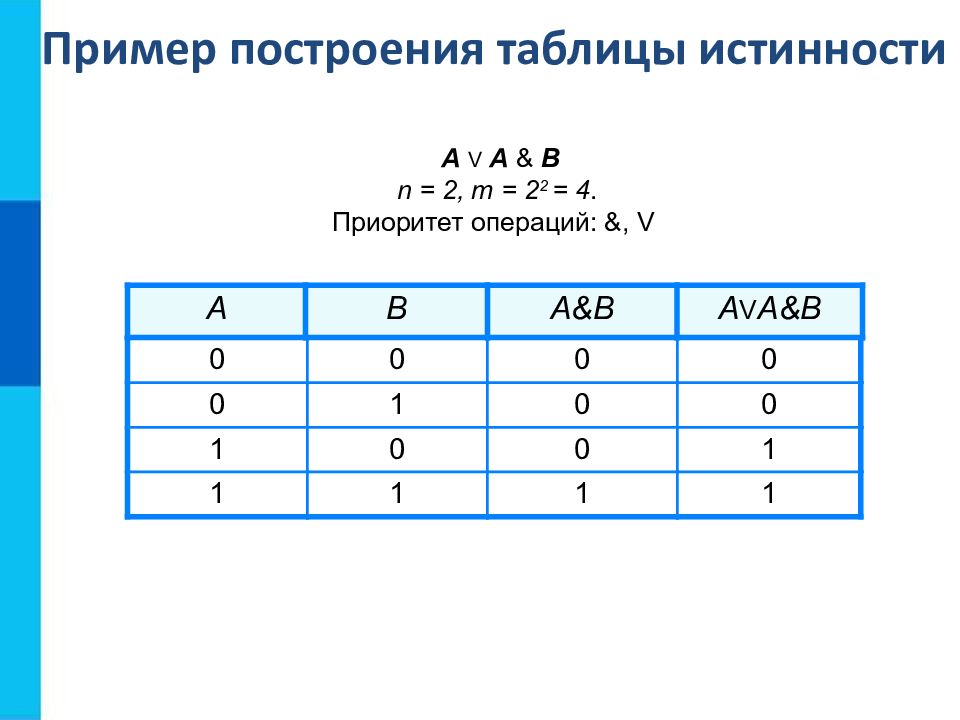
A B A&B A V A&B 0 0 0 0 0 1 0 0 1 0 0 1 1 1 1 1 А V A & B n = 2, m = 2 2 = 4. Приоритет операций: &, V Пример построения таблицы истинности
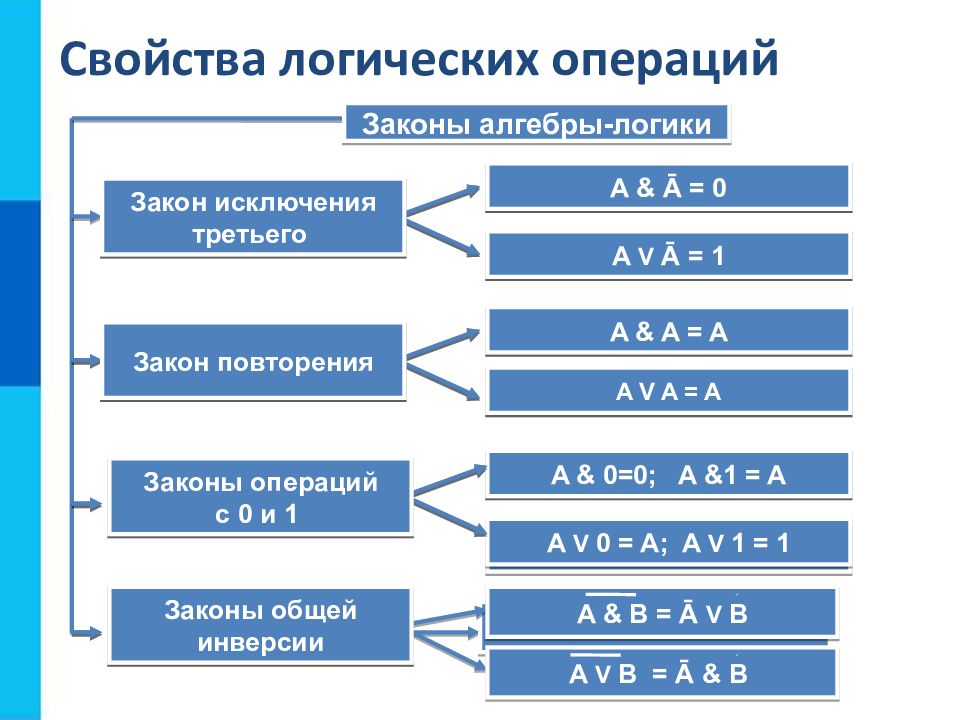
Свойства логических операций Законы алгебры-логики A & B = B & A A V B = B V A A&(B V C)= (A&B) V (A&C) A V (B&C) = (A V B)&(A V C) (A & B) & C = A & ( B & C) (A V B) V C =A V ( B V C) Переместительный Сочетательный Распределительный Закон двойного отрицания Ā = A A & Ā = 0 A V Ā = 1 A & 0=0; A &1 = A A V 0 = A; A V 1 = 1 A & A = A A V A = A Закон исключения третьего Закон повторения Законы операций с 0 и 1 Законы общей инверсии A & B = Ā V B A V B = Ā & B
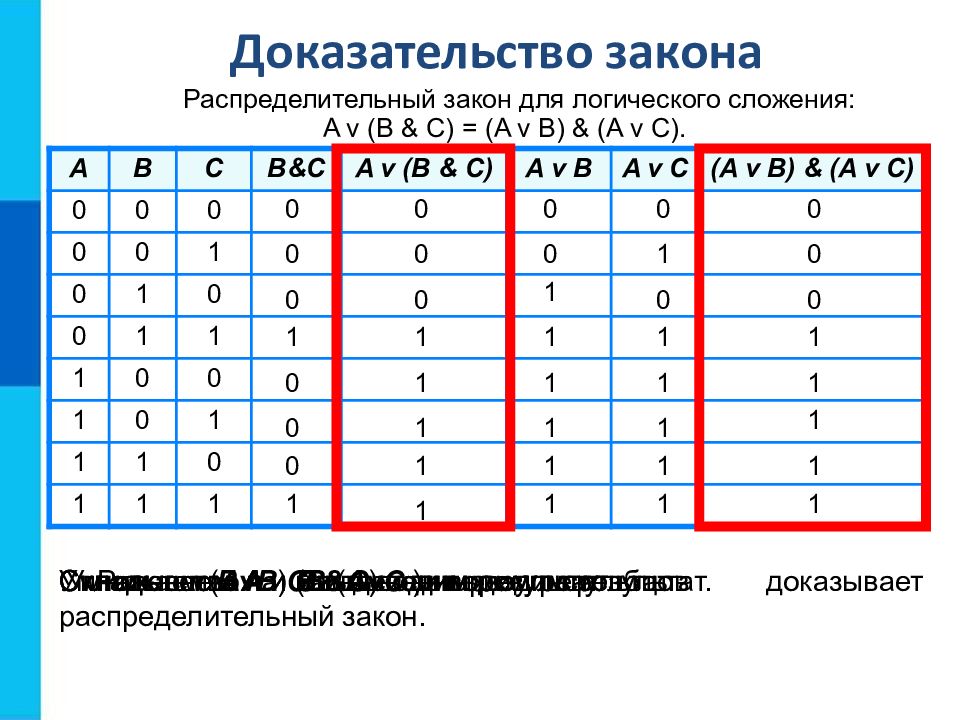
A B C B&C A v (B & C) A v B A v C (A v B) & (A v C) 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 Распределительный закон для логического сложения: A v (B & C) = (A v B) & (A v C). Доказательство закона Умножаем В на С и выводим результат. 0 0 0 0 0 0 1 1 Складываем А и В и выводим результат. 0 0 0 1 1 1 1 1 Складываем А и ( В & С ) и выводим результат. 0 0 1 1 1 1 1 1 Складываем А и C и выводим результат. 0 0 1 1 1 1 1 1 Умножаем ( А v B ) на ( A v C )и выводим результат. 0 0 0 1 1 1 1 1 Равенство выделенных столбцов доказывает распределительный закон.
Задача. Коля, Вася и Серёжа гостили летом у бабушки. Однажды один из мальчиков нечаянно разбил любимую бабушкину вазу. Решение логических задач На вопрос, кто разбил вазу, они дали такие ответы: Серёжа : 1) Я не разбивал. 2) Вася не разбивал. Вася : 3) Серёжа не разбивал. 4) Вазу разбил Коля. Коля: 5) Я не разбивал. 6) Вазу разбил Серёжа. Бабушка знала, что один из её внуков (правдивый), оба раза сказал правду; второй (шутник) оба раза сказал неправду; третий (хитрец) один раз сказал правду, а другой раз - неправду. Назовите имена правдивого, шутника и хитреца. Кто из внуков разбил вазу?
K B C Утверждение Серёжи Утверждение Васи Утверждение Коли K C 0 0 1 0 1 0 0 1 1 0 1 0 1 0 1 0 1 0 1 0 0 1 1 1 1 0 0 С В К С Решение. Пусть К =«Коля разбил вазу», В =«Вася разбил вазу», С =«Серёжа разбил вазу». Представим в таблице истинности высказывания каждого мальчика. Так как ваза разбита одним внуком, составим не всю таблицу, а только её фрагмент, содержащий наборы входных переменных: 001, 010, 100. Исходя из того, что знает о внуках бабушка, следует искать в таблице строки, содержащие в каком-либо порядке три комбинации значений: 00, 11, 01 (или 10). Это первая строка. Вазу разбил Серёжа, он - хитрец. Шутником оказался Вася. Имя правдивого внука - Коля.
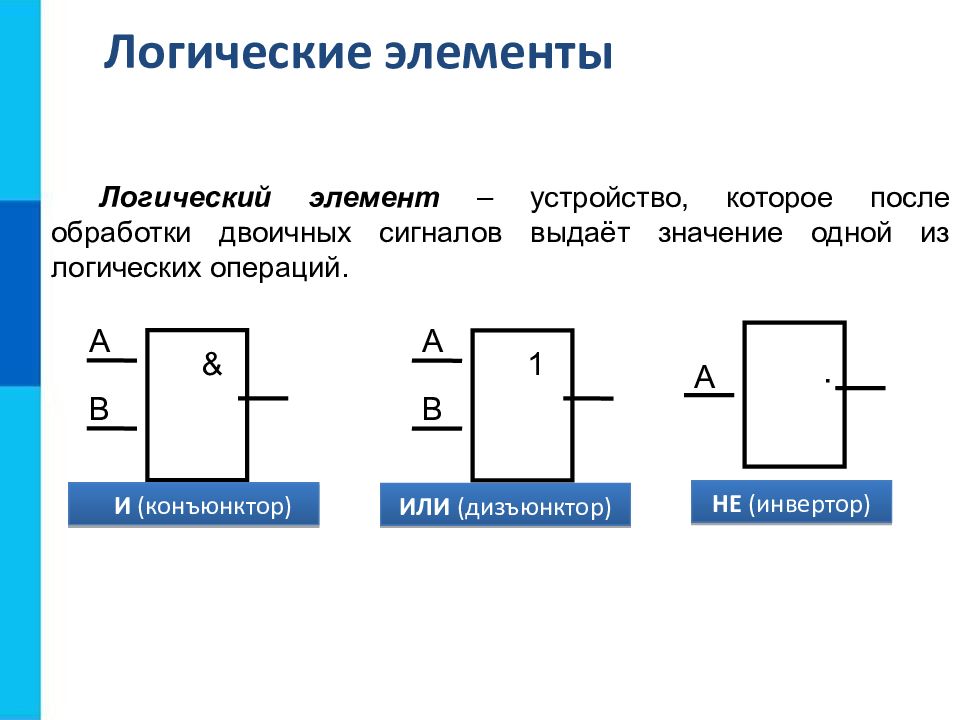
Логический элемент – устройство, которое после обработки двоичных сигналов выдаёт значение одной из логических операций. & А В И (конъюнктор) 1 А В ИЛИ (дизъюнктор) НЕ (инвертор) А Логические элементы
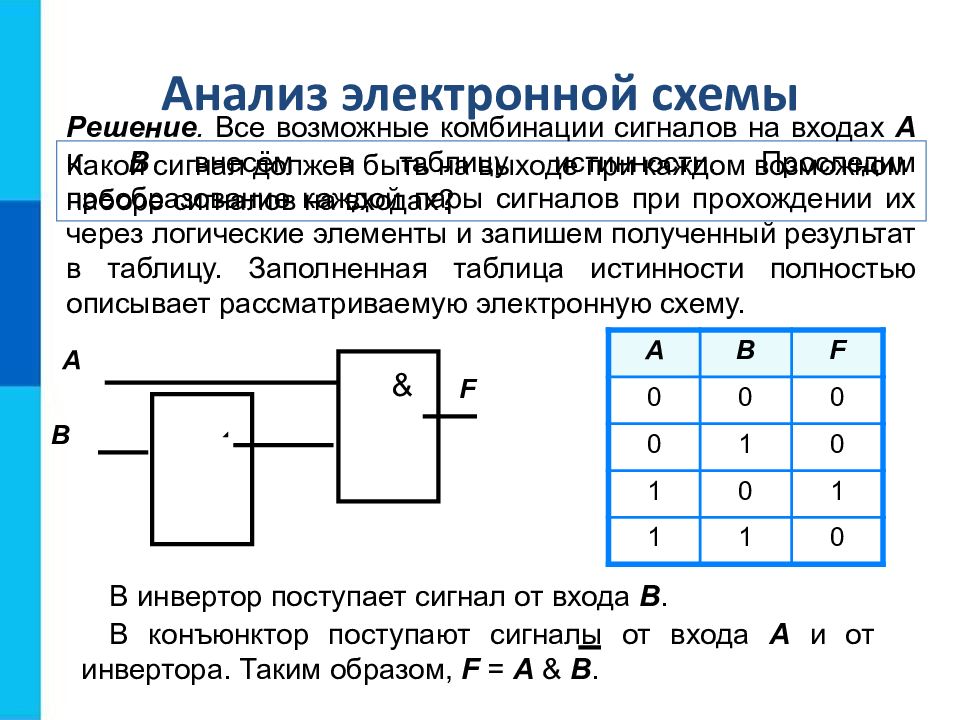
Какой сигнал должен быть на выходе при каждом возможном наборе сигналов на входах? Анализ электронной схемы Решение. Все возможные комбинации сигналов на входах А и В внесём в таблицу истинности. Проследим преобразование каждой пары сигналов при прохождении их через логические элементы и запишем полученный результат в таблицу. Заполненная таблица истинности полностью описывает рассматриваемую электронную схему. А В & F A B F 0 0 0 0 1 0 1 0 1 1 1 0 В инвертор поступает сигнал от входа В. В конъюнктор поступают сигналы от входа А и от инвертора. Таким образом, F = A & B.
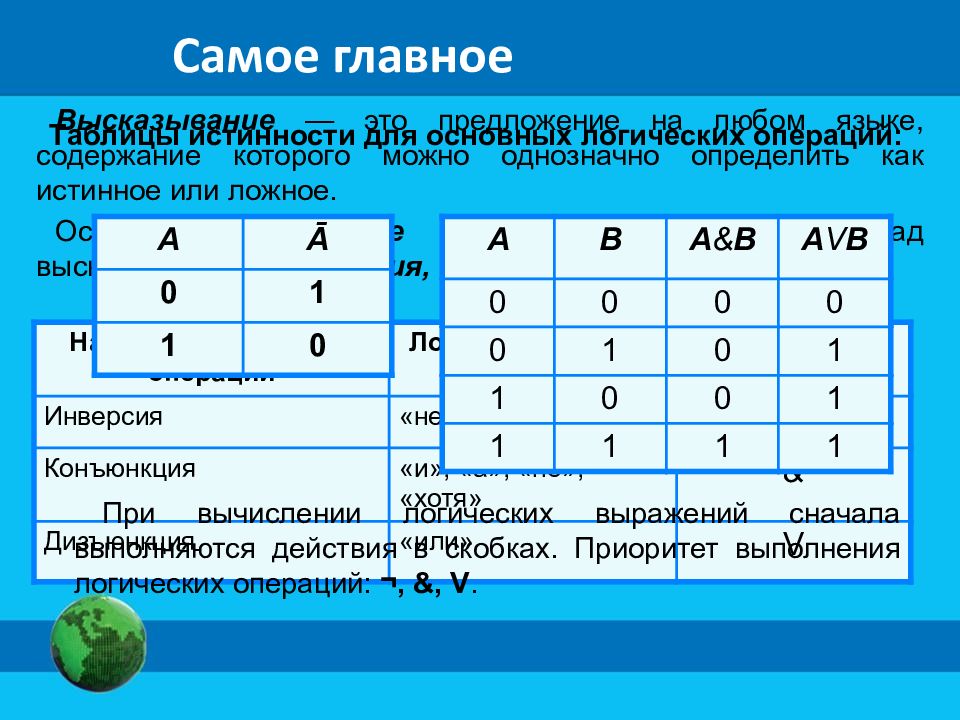
Высказывание — это предложение на любом языке, содержание которого можно однозначно определить как истинное или ложное. Основные логические операции, определённые над высказываниями: инверсия, конъюнкция, дизъюнкция. Название логической операции Логическая связка Обозначение Инверсия «не, «неверно, что» ¬, ─ Конъюнкция «и», «а», «но», «хотя» & Дизъюнкция «или» V Таблицы истинности для основных логических операций: А Ā 0 1 1 0 A B A & B A V B 0 0 0 0 0 1 0 1 1 0 0 1 1 1 1 1 При вычислении логических выражений сначала выполняются действия в скобках. Приоритет выполнения логических операций: ¬, &, V. Самое главное
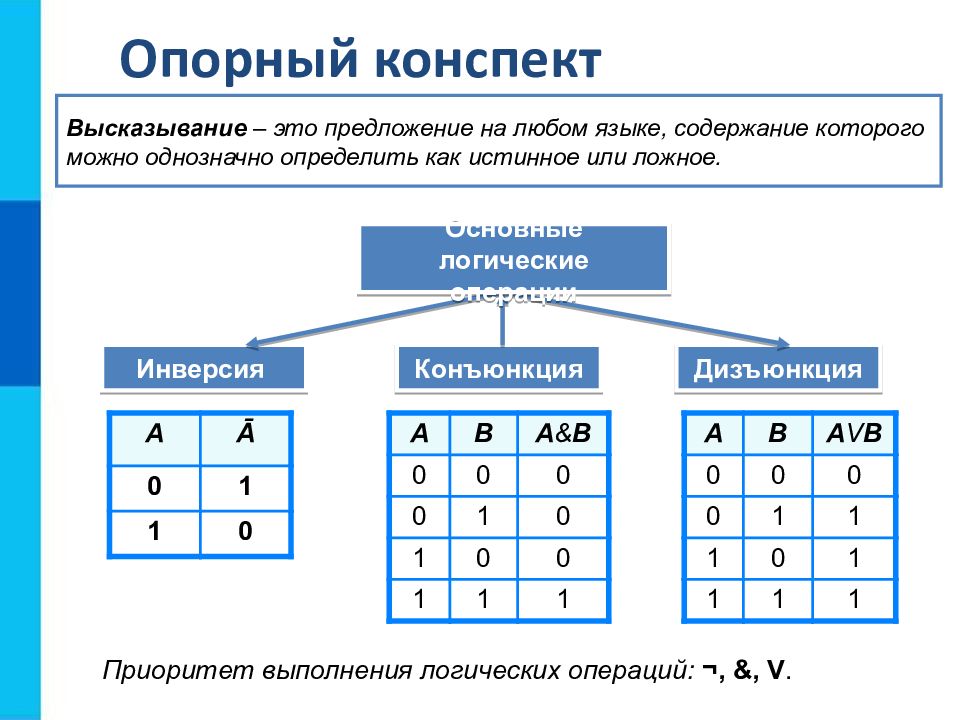
Опорный конспект Инверсия Конъюнкция Дизъюнкция Высказывание – это предложение на любом языке, содержание которого можно однозначно определить как истинное или ложное. А Ā 0 1 1 0 A B A & B 0 0 0 0 1 0 1 0 0 1 1 1 A B A V B 0 0 0 0 1 1 1 0 1 1 1 1 Приоритет выполнения логических операций: ¬, &, V. Основные логические операции
Электронные образовательные ресурсы http://school-collection.edu.ru/catalog/res/9e997f40-f285-4369-aa7d-88b892beca45/?interface=catalog&class=51&subject=19 – Элементарные логические операции
Домашнее задание Внимательно ещё раз Просмотрите материалы презентации. Прочитайте параграф 1. 4. 6 страница 47. Выполнить письменно в тетради тест на стр. 54 Работы направлять на электронный адресс omelop2907@gmail.com
