Слайд 2: Основные понятия
Логика - это наука о формах и способах мышления. Это учение о способах их рассуждений и доказательств. Понятие - это форма мышления, которая выделяет существенные признаки предмета или класса предметов, позволяющие отличать их от других. Высказывание - это формулировка своего понимания окружающего мира. Высказывание является повествовательным предложением, в котором что-либо утверждается или отрицается. Основные понятия
Слайд 3
Умозаключение - это форма мышления, с помощью которой из одного или нескольких суждений может быть получено новое суждение (знание или вывод). Логическая переменная - это простое высказывание, содержащее только одну мысль.
Слайд 4
Ее символическое обозначение - латинская буква (например, A, B, X, Y и т.д.). Значением логической переменной могут быть только константы ИСТИНА и ЛОЖЬ (1 и 0). Составное высказывание - логическая функция, которая содержит несколько простых мыслей, соединенных между собой с помощью логических операций. Ее символическое обозначение - F ( A, B...)
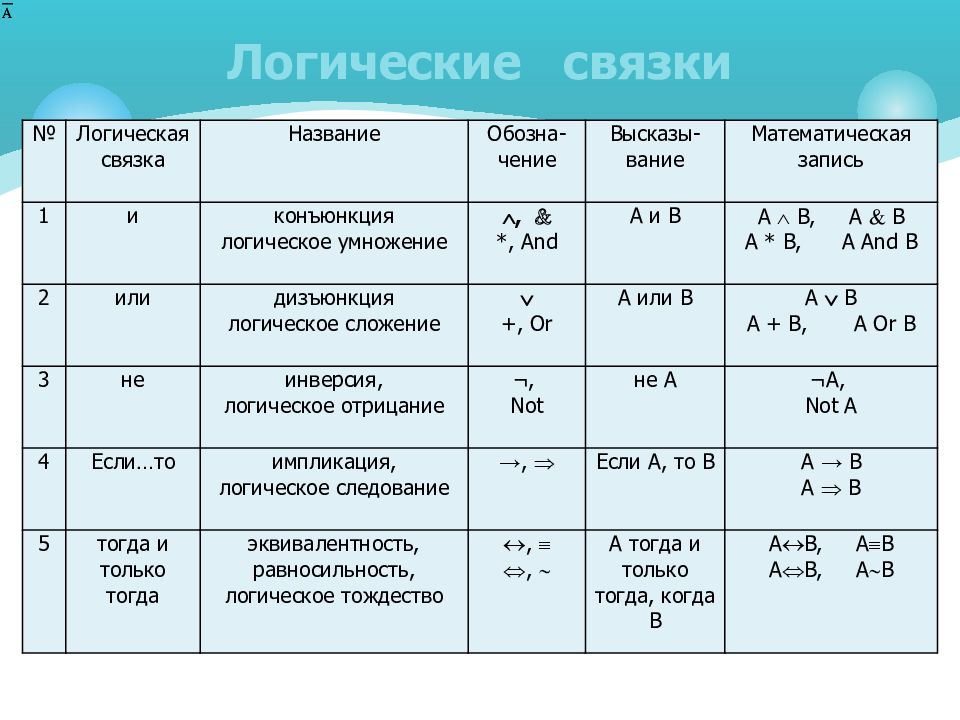
Слайд 5: Логические связки
№ Логическая связка Название Обозна-чение Высказы-вание Математическая запись 1 и конъюнкция логическое умножение , *, And A и В A B, A B A * B, A And B 2 или дизъюнкция логическое сложение +, Or A или В A B A + B, A Or B 3 не инверсия, логическое отрицание ¬, Not не А ¬А, Not A 4 Если…то импликация, логическое следование →, Если A, то В A → B A B 5 тогда и только тогда эквивалентность, равносильность, логическое тождество , , А тогда и только тогда, когда В А В, А В А В, А В Логические связки
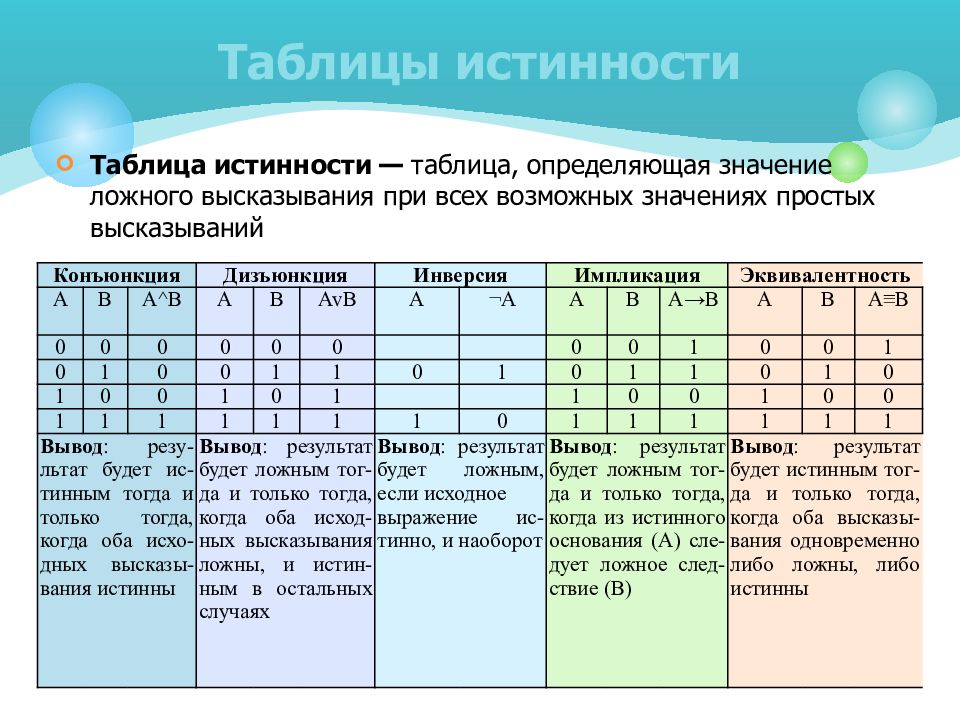
Слайд 6: Таблицы истинности
Таблица истинности — таблица, определяющая значение ложного высказывания при всех возможных значениях простых высказываний Конъюнкция Дизъюнкция Инверсия Импликация Эквивалентность А В А^В А В AvB А ¬А А В А→В А В А≡В 0 0 0 0 0 0 0 0 1 0 0 1 0 1 0 0 1 1 0 1 0 1 1 0 1 0 1 0 0 1 0 1 1 0 0 1 0 0 1 1 1 1 1 1 1 0 1 1 1 1 1 1 Вывод : резу-льтат будет ис-тинным тогда и только тогда, когда оба исхо-дных высказы-вания истинны Вывод : результат будет ложным тог-да и только тогда, когда оба исход-ных высказывания ложны, и истин-ным в остальных случаях Вывод : результат будет ложным, если исходное выражение ис-тинно, и наоборот Вывод : результат будет ложным тог-да и только тогда, когда из истинного основания (А) сле-дует ложное след-ствие (В) Вывод : результат будет истинным тог-да и только тогда, когда оба высказы-вания одновременно либо ложны, либо истинны
Слайд 7
Если составное высказывание (логическую функцию) выразить в виде формулы, в которую войдут логические переменные и знаки логических операций, то получится логическое выражение, значение которого можно вычислить. Значением логического выражения могут быть только ЛОЖЬ или ИСТИНА.
Слайд 8
При составлении логического выражения необходимо учитывать порядок выполнения логических операций, а именно: 1) действия в скобках; 2) инверсия (¬), конъюнкция (^), дизъюнкция ( v ), импликация (→), эквивалентность (≡).
Слайд 9: Для составления таблицы необходимо:
Выяснить количество строк в таблице (вычисляется как 2 n +1, где n — количество переменных). Выяснить количество столбцов = количество переменных + количество логических операций. Установить последовательность выполнения логических операций. Построить таблицу, указывая названия столбцов и возможные наборы значений исходных логических переменных. Заполнить таблицу истинности по столбцам.
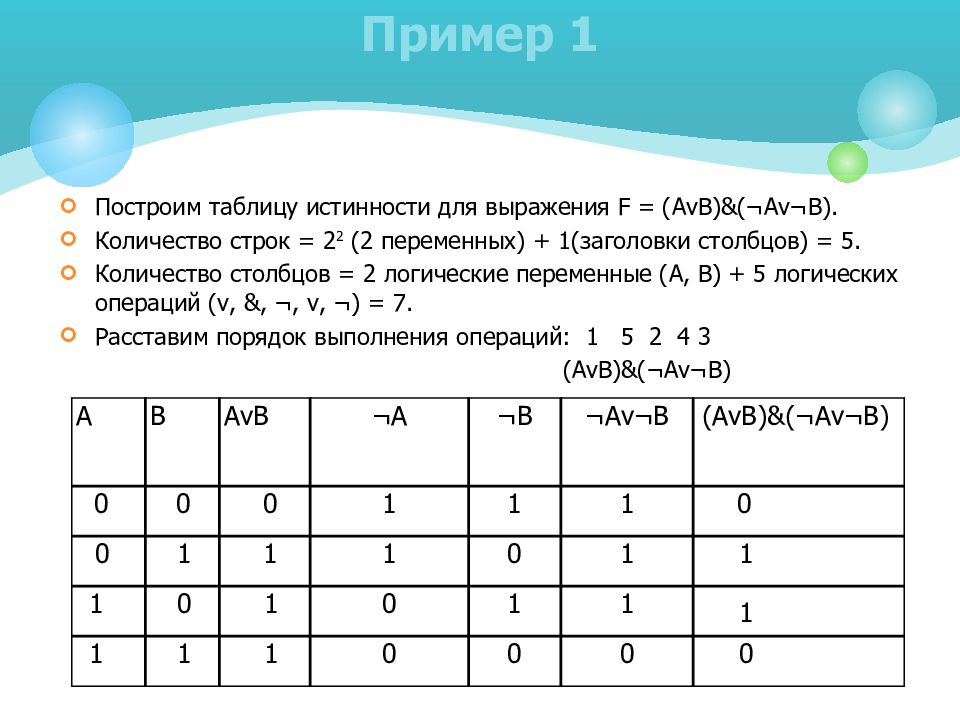
Слайд 10: Пример 1
Построим таблицу истинности для выражения F = ( AvB )&(¬ Av ¬ B ). Количество строк = 2 2 (2 переменных) + 1(заголовки столбцов) = 5. Количество столбцов = 2 логические переменные (А, В) + 5 логических операций ( v, &, ¬, v, ¬) = 7. Расставим порядок выполнения операций: 1 5 2 4 3 ( AvB )&(¬ Av ¬ B ) А В AvB ¬А ¬В ¬Av¬B (AvB)&(¬Av¬B) 0 0 0 1 1 1 0 0 1 1 1 0 1 1 1 0 1 0 1 1 1 1 1 1 0 0 0 0
Слайд 12
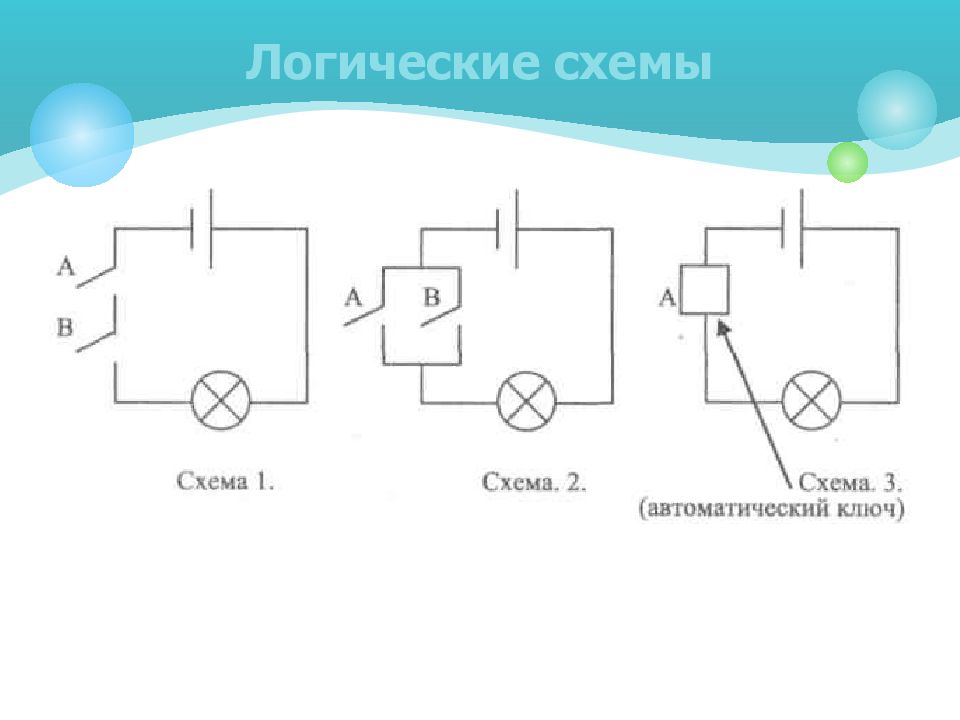
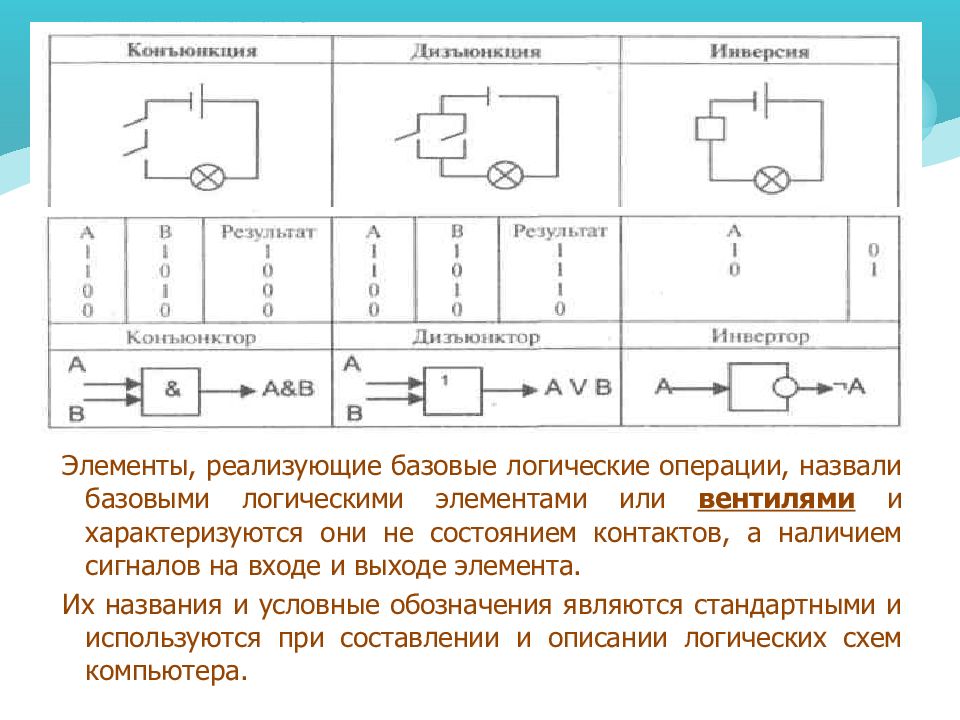
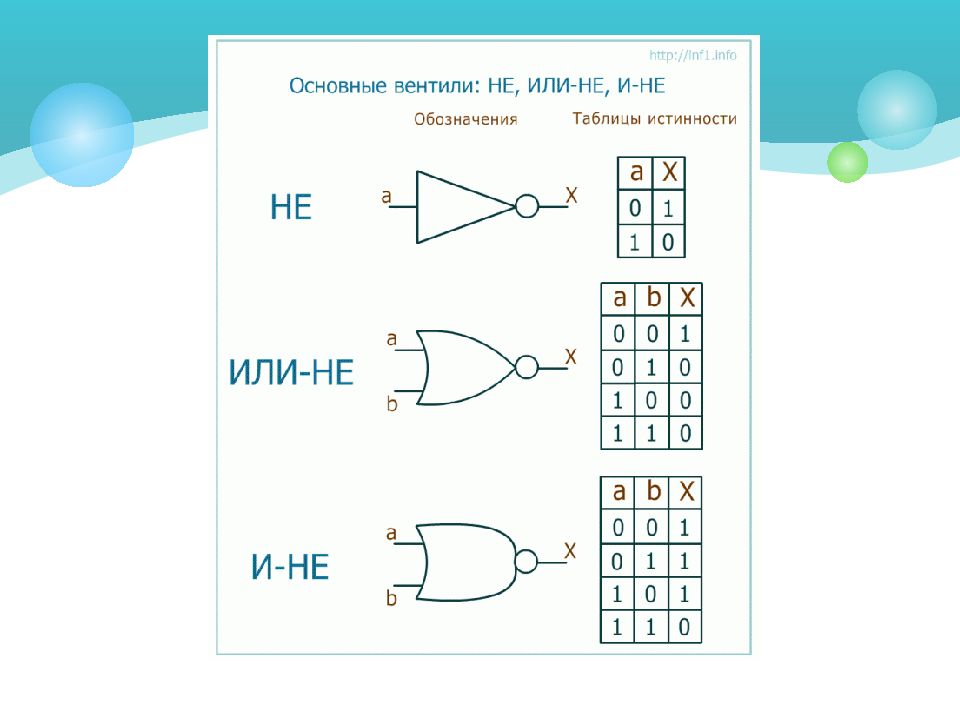
Элементы, реализующие базовые логические операции, назвали базовыми логическими элементами или вентилями и характеризуются они не состоянием контактов, а наличием сигналов на входе и выходе элемента. Их названия и условные обозначения являются стандартными и используются при составлении и описании логических схем компьютера.
Слайд 13: Правило построение логических схем
1) Определить число логических переменных. 2) Определить количество базовых логических операций и их порядок. 3) Изобразить для каждой логической операции соответствующий ей вентиль. 4)Соединить вентили в порядке выполнения логических операций. Правило построение логических схем
Слайд 14: Пример 2
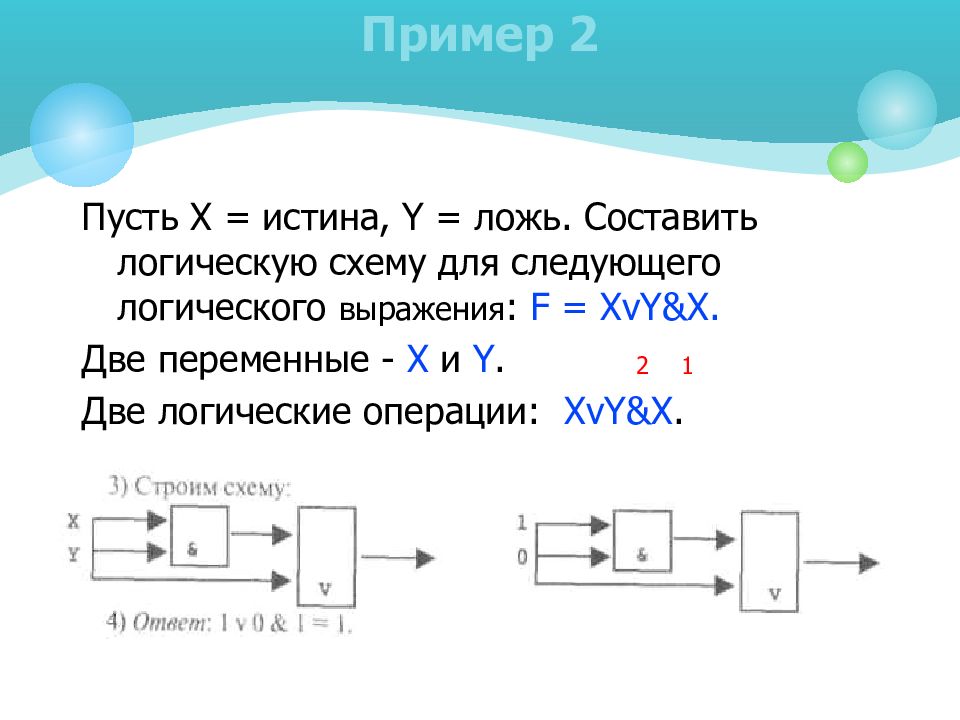
Пусть X = истина, Y = ложь. Составить логическую схему для следующего логического выражения : F = XvY & X. Две переменные - X и Y. Две логические операции: XvY&X. Пример 2 1 2
Слайд 15: Задание 1
Составьте таблицы истинности для следующих логических выражений: F = ( X &¬ Y ) vZ. F = X&YvX. F = ¬(XvY)&(YvX). F = ¬ ( (XvY)&(ZvX))&(ZvY). F = A&B&C&¬D. F = (AvB)&(¬BvAvB ) Задание 1.
Слайд 19: Задание 3
Постройте логическую схему, соответствующую логическому выражению, и найдите значение логического выражения: F=AvB& ¬ C, если А=1, В=1, С=1. F= ¬ (AvB&C), если А=0, В=1, С=1. F= ¬ AvB&C, если А=1, В=0, С=1. F= ( AvB)&(CvB), если А=0, В=1, С=0. F= ¬ (A&B&C), если А=0, В=0, С=1. F=(A&B&C)v(B&Cv ¬ A), если А=1, В=1, С=0. F=B& ¬ Av ¬ B&A, если А=0, В=0. Задание 3.
Слайд 20: Задание 4
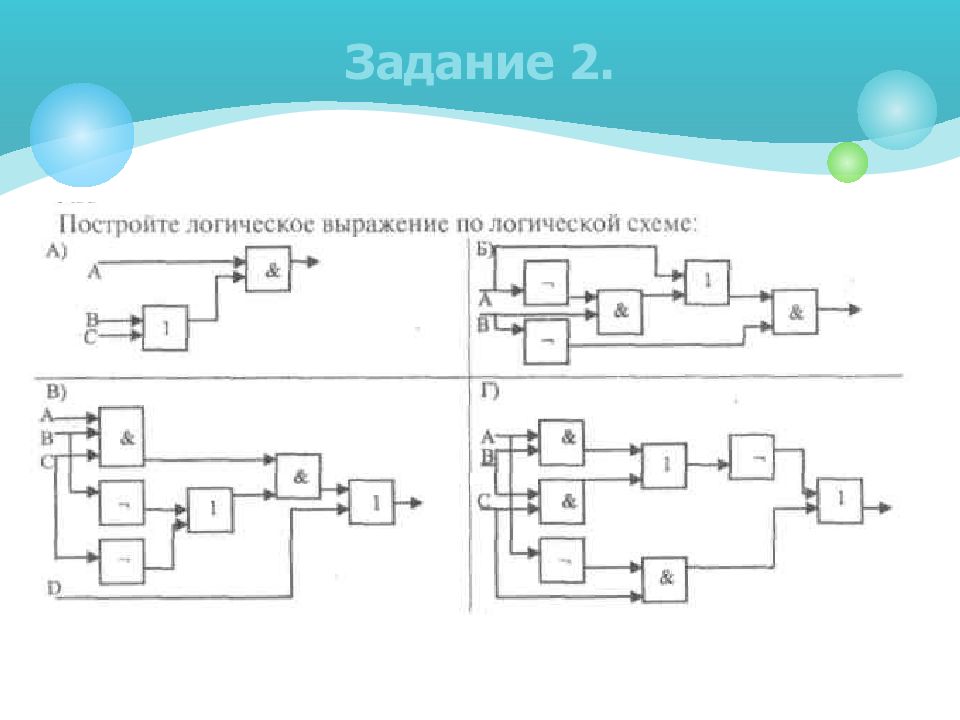
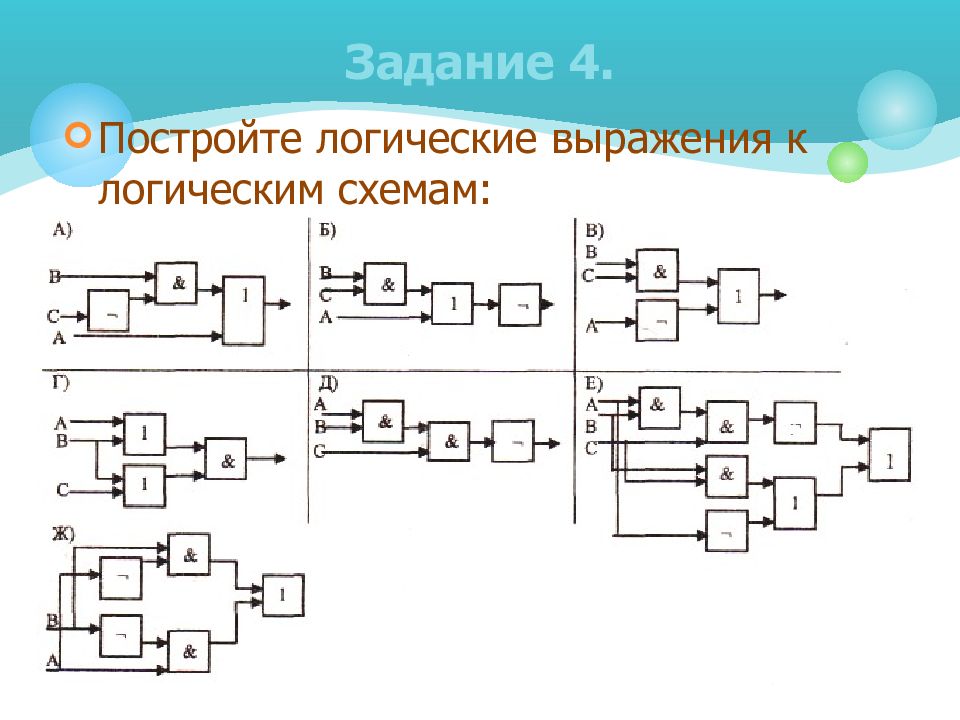
Постройте логические выражения к логическим схемам: Задание 4.